基于响应面和粒子群算法的悬置多目标优化

关 挺，钟绍华，周 才，范文涛

（1.武汉理工大学 现代汽车零部件技术湖北省重点实验室，湖北 武汉 430070；2.武汉理工大学 汽车零部件技术湖北省协同创新中心，湖北 武汉 430070）

基于响应面和粒子群算法的悬置多目标优化

关 挺1,2，钟绍华1,2，周 才1,2，范文涛1,2

（1.武汉理工大学 现代汽车零部件技术湖北省重点实验室，湖北 武汉 430070；2.武汉理工大学 汽车零部件技术湖北省协同创新中心，湖北 武汉 430070）

为了改善某厂商驾驶室悬置平顺性较差的问题，进行了实车道路平顺性实验并选出了平顺性较好的结构，并提出了一种新的优化方法优化了悬置的参数：在ADAMS中建立了参数化模型，以驾驶室地板垂向加权加速度均方值和质心俯仰加权加速度均方值作为响应评价指标，用Box-BehnkenDesign（BBD）试验设计方法进行了多次仿真，根据仿真结果得到了两个响应量的响应面，并根据最小二乘法拟合出了相应的响应多项式方程，对两个响应量取不同权重，用粒子群算法（PSO）对目标函数进行了优化。结果表明，优化后的垂向加权加速度均方值和俯仰加权加速度均方值有明显下降，系统平顺性得到提高。

驾驶室悬置；平顺性试验；响应面；最小二乘法；粒子群算法；BBD试验

1 引言

随着汽车行业和货运物流业的发展，卡车已经成为了重要的陆路大型运输工具。随着技术的进步，人们要求卡车不仅要能满足运输的基本功能，还要使乘坐者有较好的乘坐体验，这对卡车的平顺性提出了更高的要求。平顺性较差会使得乘坐者难以操控汽车，容易发生驾驶疲劳从而导致危险驾驶，并且可能与乘员身体器官发生共振从而影响人体健康，因此，近年来行业中对卡车的悬置研究不断深入，研究成果也推动了卡车悬置的性能提升。基于成本因素，国内卡车普遍装配的为被动悬置，因此这方面的研究也大多围绕着悬置的参数匹配优化而展开：文献[1]将驾驶室处理为刚性，建立了矿用车六自由度模型，同时考虑发动机和路面激励对悬置的影响，对悬置模型进行了仿真分析；文献[2]对结构相同但参数不同的悬置进行了道路测试，建立了ADAMS动力学模型，运用试验技术对悬置参数进行了优化；文献[3]分别对具有不同高度阀数量的悬置进行了实车试验，考察了高度阀对悬置性能的影响；文献[4]建立了带有驾驶室悬置和空气悬架的协同参数整车模型，以悬置参数和悬架参数为变量，利用理想参数修改法确定了6个最佳参数，用响应面法拟合了4个回归模型，得到了优化目标的最优解；文献[5]利用ADAMS软件开发了全浮式驾驶室商用车平顺性分析系统，并利用该系统对某商用车进行了平顺性分析；文献[6]提出了将正交试验技术与ADAMS中的DOE技术相结合的方法，研究了驾驶室悬置系统和主悬架系统的参数匹配问题；文献[7]对减振器阻尼值和弹簧刚度进行了建模优化；文献[8]针对三种典型的工况，建立驾驶室悬置ADAMS模型，对驾驶室参数进行了优化。通过研究上述文献发现：（1）目前大多数研究的优化方法通常是将建立的ADAMS模型直接与特定的优化方法耦合，这种方式在迭代优化计算模型仿真时耗时较长，导致优化效率不高[9]；（2）大多数的系统优化过程中，目标函数、结构参数和设计要求等都被视为确定性问题，忽略了系统的不确定性，此种确定性系统设计的结构参数具有更小的冗余度和更多的失效模式，因而比原系统有更高的失效概率[10]；（3）在对系统进行建模优化时，通常只考虑了垂向加速度作为评价指标，而未考虑对乘坐感受影响较大的车身俯仰运动，通常垂向加速度和俯仰角加速度不是统一的，同一组参数不可能使上述两个响应量同时取得最小值。

本文进行了实车道路试验，优选出较好的悬置结构后，在ADAMS中建立了仿真模型，根据BBD试验设计方法进行了多次仿真，根据仿真结果得到上述两个响应量的响应面，基于统计学的响应面方法可有效地考虑系统的不确定性，用最小二乘法拟合出了两个响应方程，考虑不同权重后，在Matlab中用粒子群算法对目标函数进行了带约束优化，使得优化后的结构性能得到提高。这种响应面法结合先进优化方法的模式，成为了工程优化的有效途径之一。

2 驾驶室悬置结构对比试验

2.1 悬置结构简介

悬置结构对其性能的表现有很大影响，包括硬点参数以及结构形式等。该厂商设计的三种后悬置结构A、B、C，如图1所示。结构A由上支架、下支架、左右侧空气弹簧减振器、左右侧横向减振器组成；结构B由左右对称的摆臂、上支架、空气弹簧减振器和下支架组成；结构C由左右侧上支架、下支架、左右空气弹簧减振器、左右侧横向减振器组成。前悬置的结构如图1(d)所示，由上支架、下支架空气弹簧减振器、横向稳定杆以及高度调节阀等组成。在前悬置结构形式不变的前提下，更换三种后悬置，进行平顺性试验。

图1 前后悬置结构

2.2 试验过程

本次试验根据《汽车平顺性随机输入行驶试验方法》的相关法规，用LMS SCADAS数据采集仪采集每个压电式传感器的振动数据，试验车为东风天龙某款商用车。试验设备包括LMS数据采集仪、PCB加速度传感器以及坐垫传感器等。

各传感器在实车位置布置情况如图2所示，包括悬置下支架四个垂向激励点、悬置上支架四个模型验证点以及驾驶室内座椅、靠背、地板三个数据采集点，用来采集x,y,z方向的加速度值。

图2 传感器布置

根据法规规定，共采集了30km/h、40km/h、50km/h、60km/h、70km/h五个车速的数据。数据处理时，用LMS.Test.Lab进行功率谱密度（PSD）计算，对加速度信号导出1/3倍频程数据计算三向总加权均方根值。各速度下的总加权加速度均方根值计算结果见表1，表1显示结构A的性能相对较好，因此选定后悬置结构A进行参数优化。其中，结构B采用横摆臂结构，在驾驶室垂直运动中摆臂运动量有限，若摆臂长度和铰接处的橡胶衬套参数匹配得不好，则会发生运动干涉，同时在各接触部位因为加工和装配误差可能会引入较大的摩擦，这些都可能导致结构B平顺性较差。结构A相比结构C的优点是：减振器组件下端采用橡胶软垫固定，驾驶室能取得更好的横向稳定性。

表1 加权加速度均方根值

3 驾驶室悬置系统参数化建模

3.1 模型参数

卡车驾驶室部分参数由该厂商提供，包括驾驶室质量、空气弹簧的线性刚度、减振器的阻尼、悬置系统各连接点的坐标、铰接衬套的刚度和阻尼。剩余的惯性参数如质心位置、转动惯量和惯性矩等已通过试验并运用质量线法计算获得[11]。

3.2 理论模型简化

振动系统的三要素是质量m、刚度k和阻尼c，卡车作为一个复杂的振动系统，要完整考虑所有自由度是十分困难的，在通常情况下，可将车架、车桥和驾驶室等机构视为刚性体，用质量体代替；将车轮、底盘悬架、驾驶室悬置、座椅悬置等减震元件简化为具有刚度和阻尼的一般弹性力学元件[6]。通常驾驶室的一阶模态在20Hz左右[12]，而悬置的偏频由下式计算：

式中，m为悬置单侧载荷，k'为等效刚度，k为线刚度，q为悬置设计时的杠杆比。

算得悬置偏频约为1.4Hz，试验所测数据显示，路面激励主要集中在5Hz以下，皆远离了驾驶室的一阶模态，因此暂不考虑驾驶室的柔性。将驾驶室通过前后悬置四点布置在车架上，传感器采集悬置四个布置点下端的激励数据作为驾驶室—悬置振动系统的输入（此激励为路面输入经底盘悬架衰减后的数据，试验中不再考虑悬置和悬架及车轮的耦合）；假设驾驶室前后悬置在垂直方向的运动是相互独立的，则驾驶室—悬置振动系统可以简化为如图3所示的六自由度振动模型。

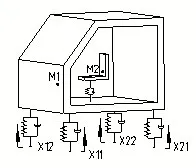
图3 驾驶室振动系统简化模型

3.3 ADAMS参数化模型

用多体动力学软件ADAMS进行建模时，进行了以下简化和假设：

（1）将驾驶室当作刚性体，刚性体在进行多体动力学仿真时，分析结果只依赖于该刚体的惯性参数，而与刚体外形无关[18]，因此将驾驶室和乘客都简化为具有相同质量和位置信息的质量小球。

（2）除横向稳定杆之外，其他构建均假设为刚体。

（3）横向稳定杆运用软件的柔性模块处理为柔性杆。

（4）悬置各连接处的橡胶衬套用软件中衬套力Bushing代替。

模型如图4所示。在模型与车架的四个连接处建立振动输入通道，以悬置下支架垂向功率谱密度（PSD）作为输入，悬置上支架的垂向PSD作为输出，验证模型的准确性。

图4 驾驶室模型

模型响应量的选择根据：（1）在三个方向的加速度中，通常垂向的振动位移在总加权加速度中所占成分最大[19]。（2）试验道路良好，因此来自于路面的激励是左右对称的，可以忽略车身的侧翻运动。因此选择了驾驶室地板垂向加权加速度均方值和质心俯仰加速度均方值作为振动响应量。加权加速度均方值按式（3）计算：

式（3）中，aw是某方向加权加速度均方根值；Ga(f)是功率谱密度函数；W（f）是某方向频率加权函数，垂向加速度和俯仰加速度的频率加权函数分别按式（4）、式（5）计算：

3.4 模型验证

取商用车常用车速60km/h，在ADAMS模型中，以该车速下采集的四个悬置下激励点垂向PSD作为输入，悬上四个点以及驾驶室脚部地板垂向PSD作为输出。初始频率设置为0.1Hz，终止频率为100Hz，仿真步长为1 000步。测试路面路况良好，悬置空气弹簧主要工作在线性区域，所以考虑空气弹簧的线性刚度，非线性工作区不考虑，由厂商提供的空气弹簧悬置线性区域参数见表2。

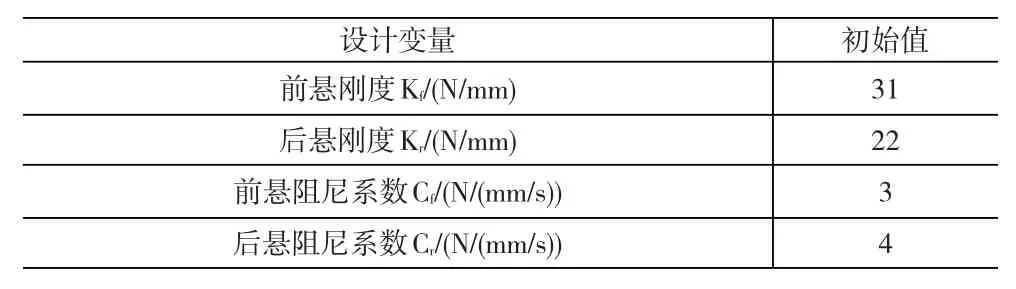
表2 悬置初参数

将仿真得到的功率谱密度与试验采集数据进行对比，结果如图5所示。

图5 不同位置模型与实际输出对比

从图5可以看出，仿真与实际共振频率基本吻合，实测值和仿真值的振动能量基本集中在2Hz～4Hz这一低频段，而共振峰值的偏差可能是由于对结构以及铰接位置作了一些简化，并且实际结构中还有一些部件是柔性部件而在ADAMS建模中进行了刚性化处理造成的；模型能满足工程精度要求，可以用于进一步参数优化。

4 响应面方程拟合

4.1 响应面法原理及方法

响应面方法（RSM）起源于统计学和数学，用来对所研究的响应量受多变量影响的问题进行模拟分析，并最终对变量进行优化[10]。它将试验设计和理论设计相结合，根据在指定区域内的若干组典型试验的结果得到响应值的近似响应面，从而可以拟合出一个明确的表达式来近似逼近隐式功能函数[13]，可用拟合出的表达式预测真实系统的响应。一旦拟合出了系统某响应值的响应面，就类似于该系统功能函数的“黑匣子”[14]，在可行域内给定输入值就能得到响应量的预测值。

响应面方法（RSM）的准确性和可靠性依赖于其拟合的功能函数的近似多项式的准确性[17]，因子的试验点必须包括最佳的试验条件，所以在进行响应面拟合之前，应该确定合理的试验因子和水平，这就需要进行试验设计，从而找出需要的典型试验点的因子水平值。经典的试验设计方法包括Box-Behnken Design（BBD）、Central Composite Design（CCD）、拉丁方试验设计和正交试验设计。其中BBD试验设计应用最为广泛，它是一种可以评价输入和响应量间非线性关系的试验方法，和CCD不同的是，它需要的试验次数更少，且在相同次数试验下，它的试验组合数比CCD方法更少、效率更高[10]。BBD方法将每个因子按1,0,-1（分别代表最大值，中心值，最小值）编码，适用于2至5个因素的试验设计。

一般地，系统响应值Y与变量x之间具有如下关系：

根据Weterstress多项式最佳逼近定理，大多数类型的函数都可以用多项式进行近似逼近[15]，多项式逼近方法可用于处理广泛的非线性问题，且表达式简单，容易实现，所以工程实际中大多采用多项式模型对系统近似逼近，此模型下系统响应与系统变量的关系为：

式中：ϑi(x)是基函数；βi是基函数系数；k是基函数ϑi(x)的个数。

工程实际应用中，通常低阶多项式就能够满足应用要求，如线性函数或者二阶多项式。一阶和二阶多项式的基本模型分别为：

式中：β为未知系数；k为设计变量个数；Y为所研究的响应值；β0为偏移项系数，βi为线性偏移系数，βii为二阶偏移系数；βij是交互作用系数。

通常在自变量的整个空间内将系统用多项式模型来近似是不现实的，但是在某个可行的小区域内却是可行的，可用最小二乘法来估计近似模型的待定参数，然后在拟合的曲面上进行RSM分析。

4.2 RSM建模及显著性分析

本实验所研究的悬置左右参数呈对称布置，空气弹簧较长时间工作在其线性刚度区域，因此本文将前后空气弹簧线性区域线刚度和阻尼器阻尼作为系统的变量，根据BBD试验设计方法，对四个变量选取典型参数组合进行了29次仿真，得到了29组两个响应量的数据，将结果导入到Design-Expert中，选择响应面选项并将多项式模型设置为二阶模型，分别得到了响应量对于四个变量的响应面，部分响应面如图6所示。

图6 响应量的部分拟合响应面

对得到的响应面用最小二乘法进行拟合，得到两个响应量的二阶多项式近似函数分别如下：

式中：aZ是地板垂向加权加速度均方值；aθx是质心俯仰角加速度均方值；Kf是前弹簧线刚度；Kr是后弹簧线刚度；Cf是前阻尼器阻尼；Cr是后阻尼器阻尼。

在用拟合的响应面方程进行预测之前，应该对多项式的显著性进行检验，以确保模型的正确性。显著性可用调整系数R2作为评价指标。

式中：SSE为响应的误差平方和；SSR为响应的回归平方和；SST为响应的离差平方和。各自的计算公式如下：

调整系数R2表达了模型变异性与总变异性的比例，越接近1表示模型越精确，但是随着拟合的多项式次数增大时，R2也会相应增大使得模型精度降低，所以引入了调整决定系数

式中：dfe表示误差的自由度；dfT表示误差综合的自由度，的值总是介于0和1之间，且越接近1越好；通常情况下，但若，则表明多项式中存在无用项需要重新拟合。除R2和可作为评价指标外，还可以对多项式进行F检验。

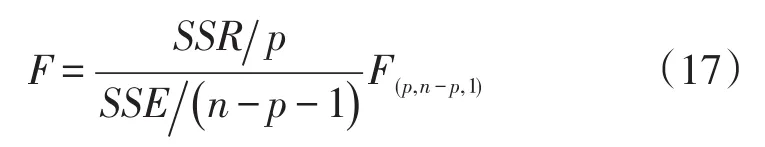
给定显著性水平α,有P{ }F＜Fα(p,n-p,1),通常α为一个很小的值，所以当F＞Fα(p,n-p,1)时是小概率事件，原假设被推翻。α越小则算出的F值越大，模型越显著。本试验拟合的多项式的各项显著性指标结果见表3。

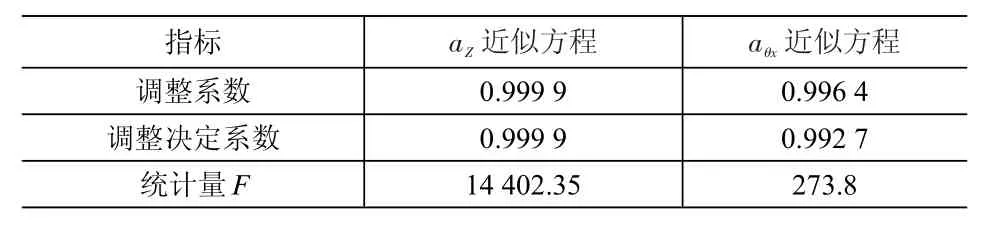
表3 显著性计算结果

取置信度α为0.01，则显著性临界值为14，所以本试验拟合的两个多项式显著性很好，可用于对实际模型的预测。根据拟合的响应面，得到az和aθx分别取到最小值时悬置的参数，见表4。

表4 响应量分别最优时的参数

由此可见，使得两个响应量分别取最小时的参数并不统一。

5 粒子群算法优化

5.1 粒子群算法原理

粒子群算法（PSO）是受到鸟类群体觅食行为而启发的一种优化算法，PSO算法每个优化问题的解都是搜索空间里的一只鸟，称为“粒子”[16]，所有粒子都有一个被适应度函数（通常为被优化的函数）决定的适应值和用于决定飞行方向和距离的速度，粒子在解空间中不断进行空间挖掘和信息共享，从而更新全局最优解，通过不断迭代最终找到最优的结果。在D维空间中进行寻优的粒子群，在每一次迭代中，各个粒子的速度和位置按式（18）、式（19）更新：

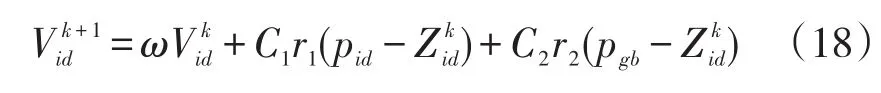
粒子每次迭代后都会根据此次迭代中的全局最优解和自身记忆的局部最优解来更新自己的速度和位置，从而在迭代完成后找到函数的最优解。在粒子的速度公式中共三项，第一项表达了粒子速度的惯性；第二项表达了粒子对自身的学习；第三项表达了粒子间的信息共享。其中第一项中惯性权重ω有着权衡局部最优位置和全局最优位置的作用，当ω较小时，群体的局部收敛能力较好；ω较大时全局收敛能力较好。所以为了得到性能更好的粒子群，应该使得ω能够随着迭代次数的增大而不断减小，这就是自适应粒子群算法（SAPSO）的原理，ω值常用式（20）进行动态调整。

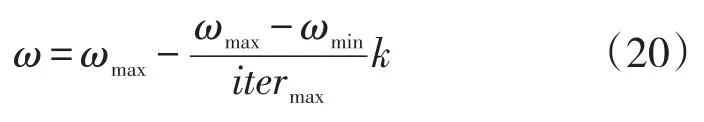
式中：ωmax和ωmin为初始权重和最终权重；itermax为最大迭代次数；k为当前迭代次数。

5.2 优化目标及约束

由于垂向加速度和俯仰角加速度的变化不统一，不能找到某一组参数使得两个响应量同时取得最小。考虑到平顺性评价方法中，垂向加速度均方值和俯仰角加速度均方值各自的轴加权系数[19]，对aZ和aθx分别赋予（0.39，0.61）的标准权重计入目标函数中，再取两组权重值（0.2,0.8）,（0.8,0.2）作为对照组1和2。根据空气弹簧制造的实际情况、承载需求以及厂商提供的气囊刚度取值范围，前后悬置的刚度取值范围有限制范围，同时对液压减振器的阻尼系数也作出了相应的限制。根据该厂商提供的实际加工限制数据，本次优化用数学语言描述为：求一组满足带约束优化方程的设计变量：Kf，Kr，Cf，Cr满足带约束优化方程：

式中：Kf，Kr，Cf，Cr分别为前后弹簧线刚度和前后阻尼器阻尼；ω1和ω2为权重值。

5.3 优化结果

在Matlab中编程对方程进行优化，粒子数量m=1 000，最大迭代次数itermax=5 000，学习因子都设置为1.496 2，惯性权重随迭代次数增大而递减，粒子各维最大速度Vmax限制为0.1倍该维自变量的上限，各维最小速度Vmin限制为Matlab的计算精度。在取标准权重的优化过程中，目标函数随迭代数的变化曲线如图7所示。

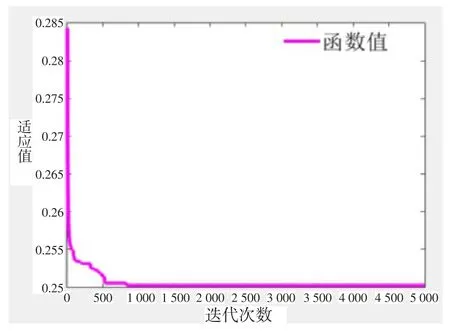
图7 全局最优解随迭代的变化趋势

粒子群算法虽然具有所需参数少、优化收敛速度快的特点，但它容易陷入局部最优解的缺点是不可忽视的，为了减小这种可能性，将程序运行了10次，取10次运行过程中的最好结果。标准权重下的优化结果和作为对比的两组对照权重下的PSO优化结果见表5。

表5 多次PSO迭代的统计结果

由于标准权重组的权重值是根据平顺性评价方法中相应的轴加权系数决定的，所以标准权重组的优化结果更具有普遍代表性，将标准权重组优化后的参数赋予模型仿真后，得到优化后的功率谱密度如图8所示。

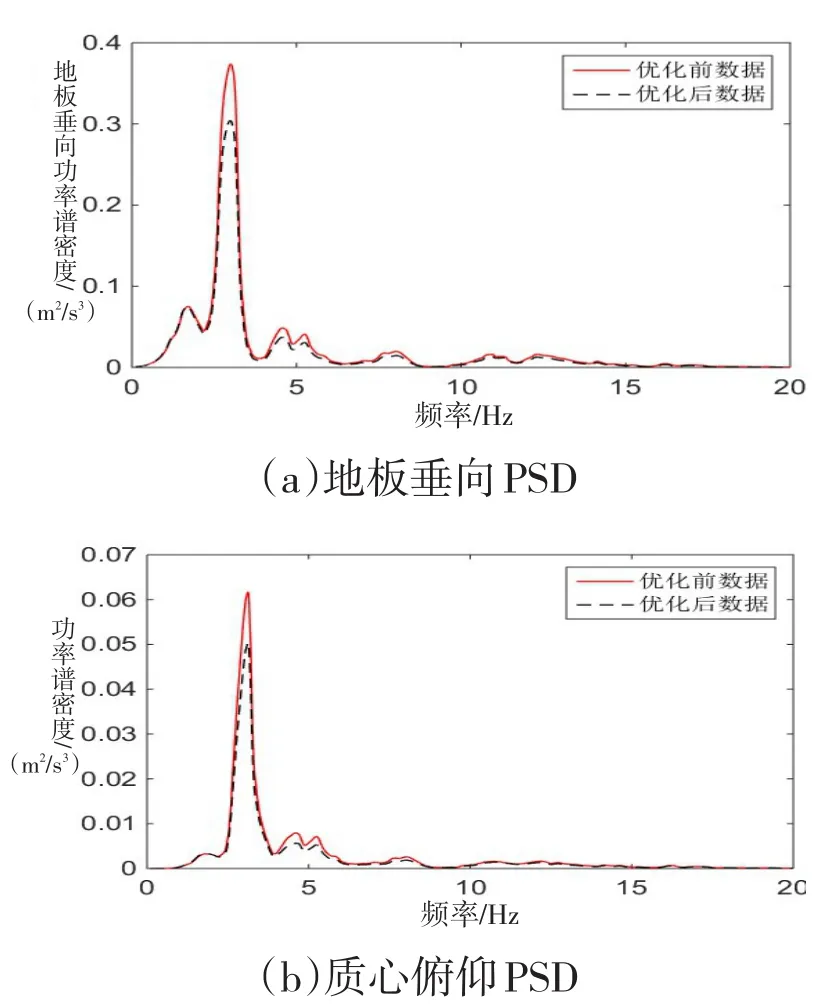
图8 标准权重下优化前后对比

作为对比，将不同权重下得到的最优悬置参数的值赋给ADAMS中的模型，加权计算得到三组权重下的垂向加权加速度均方值和俯仰角加速度均方值，见表6。

表6 优化前后响应量对比

可以看出，相对于标准权重组的结果，两组对照组的结果显示，具有更大权重的响应量在优化中提升的程度也更大。

6 结语

（1）进行了多次实车平顺性试验，计算响应的加权加速度均方根值，选出了最优的结构A。

（2）采用BBD试验设计近似得到两个响应量的响应面，用最小二乘法拟合出了近似响应面的二阶多项式并检验了多项式的显著性。对垂向加权加速度均方值和俯仰加权角加速度均值取不同的权重值，用粒子群算法对目标函数进行了优化。在标准权重下，优化后的参数使得模型的垂向加速度比优化前下降了10.46%，俯仰角加速度比优化前下降了7.67%；两个响应量各自的提升程度依赖于各自的权重值，但可以肯定的是，系统的平顺性得到了提高。

[1]李来平,罗彩煌,赵明凯,等.矿用自卸车驾驶室悬置系统动力学建模与动态激励研究[J].矿山机械,2014,(8):123-127.

[2]杨辉,张瑞亮,王铁,等.载货车驾驶室悬置系统试验仿真与优化[J].机械科学与技术,2016,(1):139-143.

[3]庞辉,李红艳,方宗德,等.驾驶室悬置系统对重型车辆平顺性影响的试验研究[J].汽车技术,2011,(11):52-56.

[4]赵林峰,胡金芳,张荣芸.重型牵引车驾驶室悬置与悬架参数的集成优化设计[J].中国机械工程,2016,(6):791-795,800.

[5]李立,马力,余晨光,等.全浮式驾驶室商用车平顺性分析系统开发[J].武汉理工大学学报(信息与管理工程版),2006,(4):71-74,92.

[6]于昌阳,马力,朱祝英,等.基于DOE技术的商用车驾驶室悬置隔振设计[J].拖拉机与农用运输车,2006,(6):15-16,19.

[7]叶福恒,许可,张延平,等.某商用车驾驶室全浮式悬置系统开发[J].汽车技术,2010,(6):33-39.

[8]杨辉,张瑞亮,王铁,等.自卸车驾驶室悬置系统试验与优化[J].汽车技术,2015,(2):4-7.

[9]蒋荣超,王登峰,吕文超,等.基于Kriging模型的驾驶室悬置系统多目标优化[J].农业机械学报,2017,(3):344-350.

[10]王万中.试验的设计与分析[M].北京:高等教育出版社,2004.

[11]周才,钟绍华,宋鹏飞.卡车驾驶室惯性参数识别试验研究[J].武汉理工大学学报(交通科学与工程版),2016,(4):755-758.

[12]刘维达,王铁,申晋宪,等.基于响应面法的驾驶室悬置系统平顺性优化[J].汽车工程,2017,(3):323-327,334.

[13]周萍,于德介,臧献国,等.采用响应面法的汽车转向系统固有频率优化[J].汽车工程,201,(10):883-887.

[14]江浩斌,刘强,耿建涛,等.基于ADAMS和响应面法的汽车悬架阻尼优化与试验[J].汽车技术,2011,(6):6-10.

[15]李莉,张赛,何强,等.响应面法在试验设计与优化中的应用[J].实验室研究与探索,2015,34(8).

[16]纪震,廖惠连,吴青华.粒子群算法及应用[M].北京:科学出版社,2008.

[17]王永菲,王成国.响应面法的理论与应用[J].中央民族大学学报(自然科学版),2005,(3):236-240.

[18]郑建荣.ADAMS虚拟样机技术入门与提高[M].北京:北京理工大学出版社,1998.

[19]余志生.汽车理论[M].北京:机械工业出版社,1981.

Multi-objective Optimization of Cab Suspension Based on Response Surface and PSO

Guan Ting1,2,Zhong Shaohua1,2,Zhou Cai1,2,Fan Wentao1,2
(1.Hubei Key Laboratory for Modern Automobile Spare Parts&Technology,Wuhan University of Technology,Wuhan 430070;2.Hubei Collaborative Innovation Center for Automobile Spare Parts&Technology,Wuhan University of Technology,Wuhan 430070,China)

In this paper,to improve the ride comfort of the cab suspension of a certain carmaker,we carried out a vehicle road test to identify the suspension structure with better ride comfort and proposed a new method to optimize the parameters of the suspension.More specifically,we established the parameterized model in ADAMS,then made the mean square value of the weighted acceleration of the floor vertical and centroid pitching directions of the cab floor as the response evaluation indexes,and performed multiple simulations using the Box-Behnken Design test methodology,through which,the response surface of the two response variables were obtained,the corresponding polynomial equation derived and the objective functions optimized.Through the simulation,we demonstrated obvious drop in both values after the optimization.

cab suspension;ride comfort test;response surface;least square method;PSO;BBD test

F224.0;F253.9

A

1005-152X(2017)10-0101-08

10.3969/j.issn.1005-152X.2017.10.021

2017-09-10

关挺（1993-），男，四川遂宁人，硕士研究生，研究方向：汽车动力学及控制。