基于Workbench的浓密机中心轴吊点位置的优化

关玉明，于 盼，李 朝，崔 佳，商 鹏

（河北工业大学 机械工程学院，天津 300130）

基于Workbench的浓密机中心轴吊点位置的优化

关玉明，于 盼，李 朝，崔 佳，商 鹏

（河北工业大学 机械工程学院，天津 300130）

针对中心传动式浓密机的中心轴整体变形、等效应变和最大应力较大的情况，介绍了一种基于Workbench优化技术进行中心轴吊点位置选取的方法.对中心轴进行受力分析，定义优化变量，将整体变形、等效应变和最大应力作为目标函数，基于Workbench的不断迭代计算得出几种优化方案和目标函数曲线图，经比较选出合适的方案，并对选取的方案做了进一步的验证.结果表明，优化后的整体变形、等效应变和最大应力有了显著的改善.

Workbench优化；中心轴；吊点位置；整体变形；等效应变；最大应力

浓密机是基于重力沉降作用的固液分离设备，通常为由混凝土、木材或金属焊接板作为结构材料建成带锥底的圆筒形浅槽，可将含固量为10%～20%的矿浆通过重力沉降浓缩为含固量为45%～55%的底流矿浆.本文讨论的浓密机为中心传动式，由液压马达驱动，动力通过减速器后传至中心轴使其转动，并带动安装在中心轴上的耙架也随之转动，这样便可搅动矿浆.在运动过程中，浆料被搅动时所产生的扭矩直接作用在耙架上，造成中心轴应发生整体变形，这对中心轴的设计带来了一定的困扰.因此，在设计中心轴时，研究合理的耙架吊点位置使得中心轴吊点处的整体变形、等效应变以及最大应力达到最优是十分必要的.

随着计算机技术的飞速发展，结构优化算法也取得了很大的发展，目前结构优化经历了较低层次的尺寸优化，较高层次的结构形式优化和如今更高层次的拓扑优化.李纯金等[1]利用遗传算法，对随车起重机折叠臂架铰点位置进行了优化，不但降低了液压缸在工作过程中所受到的最大值，而且使整个液压系统压力更趋于稳定；王琪等[2]利用粒子群算法，对双层剪式液压升降台液压缸位置进行仿真优化分析，使升降台升降更加平稳，很好地改善了其工作性能，大大提高了其使用寿命.侯忠明等[3]在ADAMS中建立参数化伸缩臂叉车模型，利用设计研究及试验设计功能对连杆变幅机构进行参数化分析，找到最优铰点位置，使得液压缸最大受力减小，实现了优化目标.曾刚[4]通过Pro/E软件中的优化设计功能对煤矿厂给料机的定位尺寸进行优化，使得更多的物料能以自溜的方式进入给料机，从而减少了地面铲车的数量及工作量，节约了成本.本文中主要针对中心轴与耙架的吊点位置建立数学模型，借助Workbench寻找最优解，得出吊点的最优位置，以达到优化的目的.

1 静力学分析

本文讨论的新型浓密机为中心传动式，中心轴与耙架的安装关系如图1所示，在浓密池的正中央安有一根中心轴1，中心轴的末端固定有一个十字形耙架，耙架有长短耙架之分，2组耙架对称地安装在中心轴上，耙架的下端装有刮板，耙架与地面成9°角.

1.1 力学模型的建立

由于耙架对称安装，长短耙架的吊点位置位于同一水平高度，为了提高软件的运算效率，本文以一端耙架的吊点位置为主进行分析计算.图2为中心轴与耙架的机构简图，以O点为坐标原点，吊点处为A，在Y轴上，A点坐标记为（0，d），短耙架吊点处为B，记为（xB，yB）=（5.685，1.641），OB与Y轴夹角为81°，AB与X轴的夹角记为θ.浓密机工作时，耙及耙架需要克服浆液对其产生的扭矩T1.

由图2可以看出中心轴吊点处的拉力与短耙架吊点处的拉力互为一对作用力与反作用力.因此，可利用短耙架的求解来计算中心轴吊点处的受力.对中心轴和短耙架进行静力学分析得：

式中：T为驱动装置对中心轴的扭矩，N·m；T1为浆液对短耙架整体的最大扭矩，N·m；F为中心轴吊点处的处所受到的拉力，N；F′为短耙架吊点处所受到的拉力，N.

1.2 短耙架静力学分析

浆液对短耙架整体的最大扭矩T1可以认为是由耙架所受的扭矩TZ与耙所受的扭矩Tl叠加作用产生[5]，即

1） 耙架扭矩分析

耙架和耙转动范围的浆液浓度较低，该区域浆液按流体分析.耙架与中心轴相连，其运动轨迹是圆柱体，如图3所示.耙架在运动过程中要克服浆液对其的屈服应力和周围一定区域内浆液对其的剪切应力，因此，耙架所受到的扭矩TZ是剪切圆柱体侧面的扭矩Ts和上下端面的扭矩Te的总和[5].将扭矩表示为剪力的函数为：

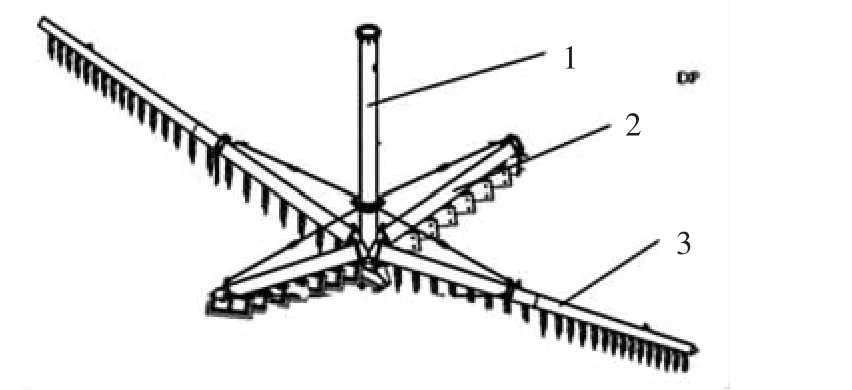
图1 中心传动式浓密机传动件模型图Fig.1 The model of the transmission part of the central drive thickener

图2 中心轴与耙架的机构简图Fig.2 Schematic diagram of the central shaft and harrow frame

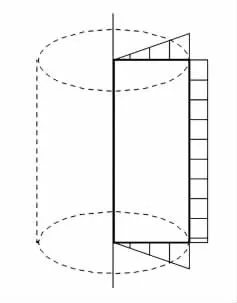
图3 耙架运动轨迹及应力分布Fig.3 Track and stress distribution of the harrow frame

式中：τs为耙架侧面处的剪切应力，Pa；τe为耙架上下端面处的屈服应力，Pa；l为耙架的长度，m，l=5.917 m；r为剪切圆柱体的半径，m，r=lcos81°；δ为剪切圆柱体的高度，m，δ=H=0.303 m.

由于耙架接触部分流动的浆液浓度基本相同，而且耙架高度不大，因此认为耙架上下端面以及侧面所受剪切应力大小相等，如图3所示，即耙架所受剪切应力为τ0=τs=τe=50 Pa[6-7].

2） 耙的扭矩分析

耙的运动轨迹是圆环体，如图4所示，因此会产生内外圆面和上下端面4个剪切面.由于耙与耙架相连，在对耙架进行分析时，已经对圆环体的上端面进行了分析，所以在这里省去这一部分的计算.耙运动时的最大扭矩表示为屈服应力的函数为

式中：τy为耙的屈服应力，Pa，τy=50 Pa；h为耙的高度，m，h=0.6m；k为耙的个数，k=7；ri1和ri2分别为第i个剪切内圆柱面与外圆柱面的半径，m.

根据以上分析，可以得出浆液对短耙架整体的最大扭矩T1的应力函数表达式

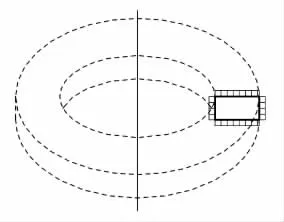
图4 耙运动轨迹及应力分布Fig.4 Trajectory and stress distribution of harrow

短耙架受力分析如图5所示.对其进行静力学分析，得出如下方程组：

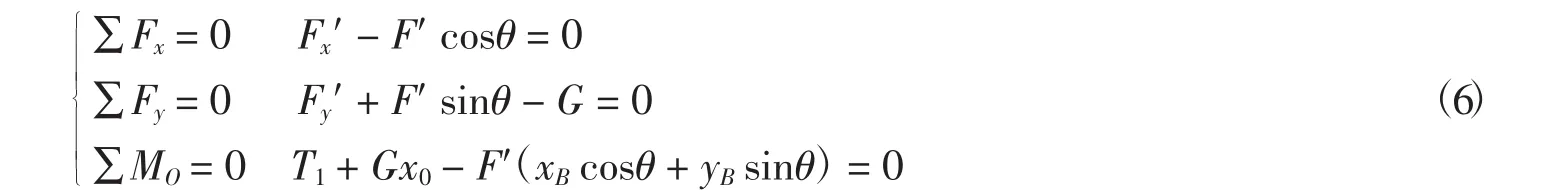
式中：F′为铰点处的作用力，N；G为短耙架与耙的重力，N，G=2 038 N；x0为耙架与耙的质量中心，m，x0=3.098m；θ为拉杆与x轴的夹角，cosθ=0.999 1，sinθ=0.02.

联立式（1） ～式（6），计算得出中心轴受到来自驱动的扭矩T=82 100 N·m，中心轴铰点出的拉力F=15 472 N.

图5 短耙架受力分析图Fig.5 Force analysis of short frame

2 ANSYS Workbench优化设计

ANSYS Workbench是利用APDL（参数化设计语言）对结构设计的参数进行调整，它要求优化的模型必须为参数化模型.优化的是通过算法不断的循环“分析——评估——修正”[8]来实现的.ANSYS优化模块中常用的算法有零阶法、一阶法、随机搜索法、最有梯度法[9]，其中，随机搜索法完成指定次数的迭代分析，可以合理确定优化空间[10-11]，是零阶法和一阶法的其前期处理步骤；零阶法通过随机搜索建立状态变量，使其与目标函数逐步逼近，广泛适用于各类工程问题，但是其收敛速度较慢[12]；一阶法的结果准确，但是计算量大，容易陷入局部最优解.

综合考虑各种优化算法的特点，本次优化设计决定使用零阶法优化算法对模型进行求解运算.

图6是中心轴的三维模型图，为了提高运行效率，在建模过程中对模型进行了简化，忽略了一些局部特征.中心轴的外形尺寸为：长度7 110 mm，直径457 mm.

使用Workbench对原有中心轴进行分析，得出如图7所示整体变形云图.中心轴在启动瞬时所受到的扭矩最大，因此研究在该时刻中心轴的整体变形是有必要的.由图7可以看出，中心轴最大变形量达到0.001 239 2 m，位于与减速器连接的部位，在结构改进时应保证具有较小的整体变形量.

图6 中心轴模型图Fig.6 Central axis model

2.1 参数化建模

参数化建模基本步骤如下.

1） 定义材料属性.中心轴的材料为Q235，材料属性见表1.

2）施加约束条件.中心轴受到来自驱动的扭矩T=82 100 N·m和吊点处的拉力F=15 472 N，在Workbench施加力时将拉力分解为Y轴和X轴的力Fx=-15 458 N，Fy=-309 N（说明：负号表示力的方向与坐标轴正方向相反）.

3） 网格划分.由于中心轴尺寸较大，结构复杂，为了提高运算效率，设置Sizing（单元尺寸）为Medium.划分网格设置完成后，中心轴被划分为73 509个节点，33 060个有限单元.

4） 参数化设置.参数化设置见表2.

表2 铰点处参数化设置Tab.2 Parameterized setting of hinge points

2.2 结果分析

利用Workbench进行结构优化，根据各变量取值范围，优化软件进行迭代计算得到12个设计点方案，计算得出整体变形对设计点的曲线图8a）、最大应力对设计点的关系曲线图8b）和等效应变对设计点的曲线图8c） .

由图8a）可以看出，在设计点2处，中心轴的整体变形达到最小，因此将设计点2作为一个候选点.由图8b）和图8c）可以看出，在设计点7处等效应变和最大应力均达到最小值，因此将设计点7作为一个候选点；另外，等效应变和最大应力对设计点的曲线最后都收敛于设计点12，表明Workbench将设计点12作为最优方案，因此将设计点12也作为一个候选点.综合分析图8可以得出3个设计点，各自优化后的数据如表3所示.

图7 原有中心轴整体变形云图Fig.7 Overall deformation of the original central axis

表1 Q235材料属性表Tab.1 Q235 material properties table

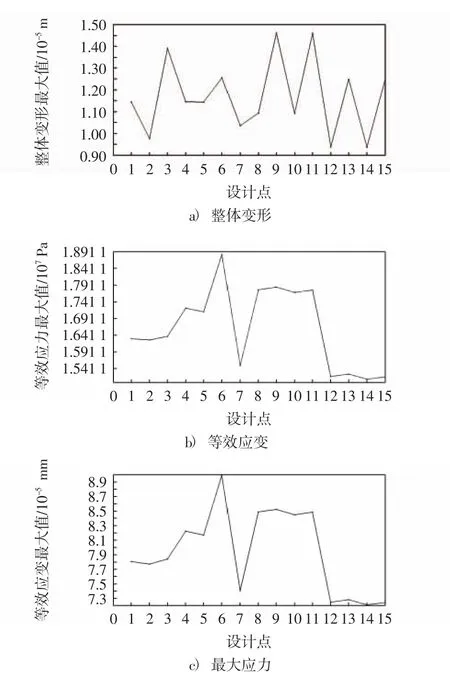
图8 目标变量对设计点的曲线图Fig.8 The curve of the target variable to the design point

根据表3数据可以看出，设计点12处的综合效果更优，因此选择设计点12作为本次优化的方案.

由图9可以看出，优化后的吊点拉力明显降低，整体变形量的最大值减小了24%，等效应变减小了31%，最大应力减小了31%，这显著提升了中心轴的工作稳定性.

3 总结

使用ANSYS Workbench对浓密机中心轴吊点位置在满足使用要求的情况下进行了整体变形、等效应变和最大应力最小值的优化设计，在得出的方案中根据实际要求选取了最佳方案，并进一步证明了方案的可行性.同时，也证明了使用ANSYS Workbench对结构进行优化的方法是可行的.这种优化方法操作简单，计算快捷，为结构优化提供了新的方法.

表3 优化设计点Tab.3 Optimal design points

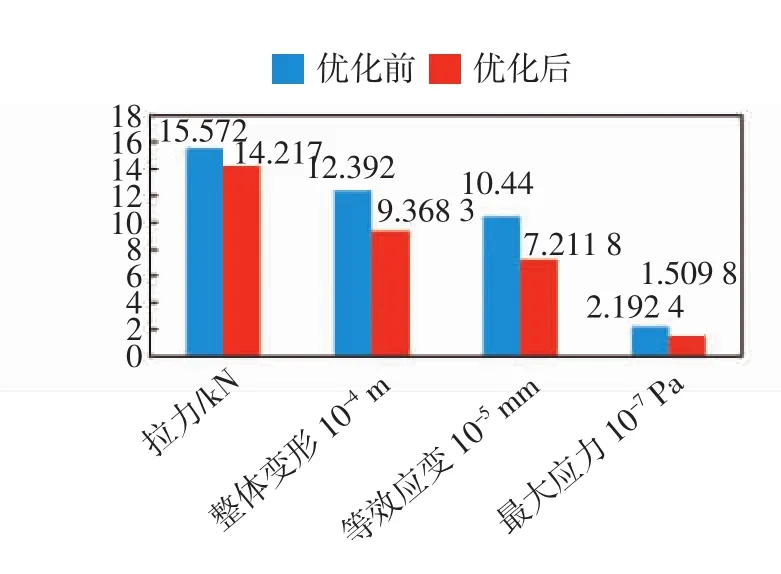
图9 优化前后数据对比Fig.9 Comparison of data before and after optimization

[1] 李纯金，褚月桥，周海波.基于遗传算法随车起重机折叠臂架铰点位置优化[J].江苏科技大学学报（自然科学版），2014，28（1）：30-36.

[2] 王琪，张任，刘建，等.基于粒子群算法的双层剪式液压升降台液压缸位置的多目标优化问题研究[J].机械科学与技术，2015，34（8）：1229-1234.

[3] 侯忠明，王胜军，辛涛.基于ADAMS的伸缩臂叉车铰点位置优化设计[J].起重运输机械，2009，23（6）：42－44.

[4] 曾刚.基于Pro/E的堆煤场给料机位置优化设计[J].煤矿技术，2014，33（10）：200-201.

[5] 吴爱祥，焦华喆，王洪江，等.深锥浓密机搅拌刮泥耙扭矩力学模型[J].中南大学学报（自然科学版），2012，43（4）：1469-1474.

[6] 李辉，王洪江，吴爱祥，等.基于尾砂沉降与流变特性的深锥浓密机压耙分析[J].北京科技大学学报，2013，35（12）：1553-1558.

[7] 王勇，王洪江，吴爱祥.基于高径比的深锥浓密机底流浓度数学模型[J].武汉理工大学学报，2011，33（8）：113-117.

[8] 徐钊，钱作勤，张平，等.基于ANSYS优化技术的换热器法兰的结构设计[J].石油和化工设备，2009（6）：15-18.

[9] 夏卫明，骆桂林，嵇宽斌.ANSYS优化算法的研究及其在液压机优化设计中的应用[J].锻压装备与制造技术，2010（1）：43-47.

[10]陆山，鲁冯杰.基于ANSYS的整体叶盘结构优化设计[J].航空动力学报，2012，27（6）：1218-1224.

[11]李伦未，陆山.基于ANSYS的多辐板风扇盘结构优化设计技术[J].航空动力学报，2011，26（10）：2245-2250.

[12]寇剑锋，郑锡涛，彭兴国.基于零阶优化方法的无人机复合材料进气道结构优化与分析[J].机械强度，2008，30（6）：1018-1022.

Optimization of hanging point position of thickener center shaft based on Workbench

GUAN Yuming,YU Pan,LI Zhao,CUI Jia,SHANG Peng

（School of Mechanical Engineering,Hebei University of Technology,Tianjin 300130,China）

A method for the selection of the hanging point position of the center shaft based on the Workbench optimization technique is introduced on the matter of the center shaft of the central drive thickener,such as the total deformation,the equivalent strain and the equivalent stress maximum.Force analyses are conducted on the center shaft and the optimization variables are defined.Put the total deformation,the equivalent strain and the equivalent stress maximum as the output variables.Several optimization schemes and the diagrams of the hinge point position with the optimization goal are obtained through the continuous iterative calculation of Workbench.The optimal scheme is chosen in accordance with the chart.Finally,further validation of the selected scheme is made.The results show that there is a big improvement in the optimization of the total deformation,the equivalent strain and the equivalent stress maximum.

Workbench optimization;center shaft;hinge position;the total deformation;the equivalent strain;the equivalent stress maximum

TH133.2

A

1007-2373（2017） 05-0028-05

10.14081/j.cnki.hgdxb.2017.05.005

2017-03-28

天津市科技特派员项目（14JCTPJC00532）

关玉明（1957-），男，教授，gyuming@163.com.

[责任编辑 杨 屹]