基于Levy飞行策略的自适应改进鸟群算法

杨文荣，马晓燕，边鑫磊

（河北工业大学 省部共建电工装备可靠性与智能化国家重点实验室，天津 300130）

基于Levy飞行策略的自适应改进鸟群算法

杨文荣，马晓燕，边鑫磊

（河北工业大学 省部共建电工装备可靠性与智能化国家重点实验室，天津 300130）

针对新型生物启发式群智能算法—鸟群算法（BSA）因进化初期种群多样性不足，以及认知和群体行为调节参数的改变而导致在优化小部分多极值函数时种群收敛精度变差、收敛迭代次数偏大甚至出现早熟收敛、陷入局部最优的问题，提出了Levy自适应改进鸟群算法（LSABSA）.该算法采用Levy飞行策略的随机游走模式来增加种群多样性和跳出局部最优值，并通过（0，1）随机均匀分布自适应改进惯性权重以及线性调整认知和社会系数来平衡BSA算法的全局和局部搜索能力，进而提高求解精度.最后采用10个典型测试函数对LSABSA算法以及粒子群算法（PSO）、改进粒子群算法（GPSO）和鸟群算法（BSA）进行仿真实验和分析对比，表明了LSABSA算法的收敛速度、精确度和稳定性均优于其他算法.

鸟群算法；Levy飞行；（0，1）随机均匀分布；线性调整；仿真测试

0 引言

因利用传统优化算法难以快速和高效地解决现实生活中的例如非凸的和不可微的复杂优化问题，受自然界生物进化和选择等抽象行为的影响，元启发式群智能优化算法日益兴起，如仿效生物界“物竞天择，适者生存”法则寻优的微分进化算法（DE）[1]、源于对鸟类捕食行为研究的粒子群算法（PSO）[2]，模拟鱼类觅食、聚群、追尾和随机等行为寻优的人工鱼群算法（AFSA）[3]，以及果蝇优化算法（FOA）[4]、鸡群算法[5-6]等，上述智能算法虽能够求解一些复杂优化问题，但在解决超高维多极值优化模型时，易早熟收敛和陷入局部最优解，因此有必要研究更有效的通用智能算法.

鸟群算法（Bird Swarm Algorithm，BSA）是Meng Xian-Bing等人在2015年提出的一种新型生物启发式全局优化算法，来源于对鸟群觅食、警惕和飞行行为的模仿以及对鸟群觅食过程中共享信息的研究，具备调节参数少、收敛精度高和鲁棒性能好等特点，已验证该算法在优化函数方面优于PSO和DE算法[7].BSA算法现已应用在微电网系统的微电源优化调度[8]、梯级水库群优化调度[9]和优化投影寻踪回归的模型参数[10]等方面，且将会应用到更广阔的领域中.BSA算法在种群进化初期多样性不足，在解决小部分多极值函数（如Ackley函数）优化问题时会出现局部收敛的情况，同时BSA算法的认知和社会行为调节参数的变化易导致种群收敛精度变差和收敛迭代次数偏大，因此需要对BSA算法进行改进.

本文借助Levy飞行行为的短距离频繁搜索和长距离少数搜索这种随机游走的特性初始化鸟群空间位置，以此扩大搜索范围、丰富种群多样性、跳出局部最优解，同时采用（0，1）随机均匀分布自适应对惯性权重取值以及线性调整学习系数，来提高收敛速度和搜索精度，即基于Levy飞行策略的自适应改进鸟群算法（Levy Self-adaption BSA，LSABSA）.最后，利用10个经典测试函数对LSABSA与PSO、GPSO和BSA算法进行仿真并进行对比分析，所得数据结果和收敛特性曲线验证了本文LSABSA算法的有效性.

1 鸟群算法仿生学基本原理

BSA算法是根据鸟类觅食、警惕和飞行行为衍生出的生物启发式算法，这些社会行为和活动的本质是群体智能，鸟群从社会活动中获取食物的最佳位置即对应于目标函数中寻找最优解.鸟类的行为简化规则如下.

规则1：每只鸟随机决定在警惕和觅食行为之间转换身份.

规则2：当选择觅食时，鸟类及时记录和更新该个体和种群先前最好的觅食位置，并以信息的方式共享于整个种群，以此来更好的寻找食物.

规则3：当保持警惕状态时，每只鸟都试图向种群的中心位置飞去，此行为受到群体间竞争的干扰，高储备量的鸟类更容易飞到种群的中心位置.

规则4：鸟类会定期飞到另一个区域，当到达终点时，鸟类将会在生产者和乞食者之间转换角色，食物储存量多的为生产者，反之为乞食者.其他鸟类则随机选择成为生产者或乞食者.

规则5：生产者积极寻找食物，乞食者则随机跟随生产者寻找食物.

1） 觅食行为

规则1为随机决策，若rand（0，1）＜P（p∈（0，1）），鸟类选择觅食，否则保持警惕.

每只鸟由自身和群体的经验来寻找食物，规则2用数学公式表示如下

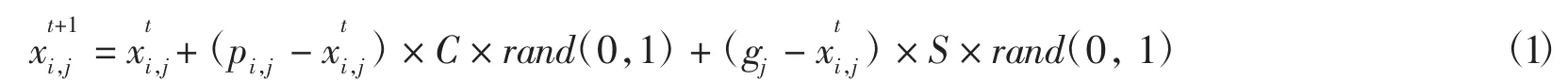
式中：j∈ [1，…，D]，rand（0，1）代表（0，1） 之间的独立均匀分布数，C和S（C、S＞0） 分别称作认知系数和社会系数.Pi，j是第i只鸟的先前最优位置，gj代表种群的先前最优位置.

2） 警惕行为

根据规则3，鸟类在保持警惕行为时会试图飞向种群的中心位置，此时鸟群之间会发生竞争关系而不会直接飞向种群的中心，这些行为用如下公式表示

式中：k（k≠i）是 [1，N]之间的随机正整数，a1、a2∈ [0，2]，pFiti代表第i只鸟的最佳适应度值，sumFit代表种群最佳适应度值之和，ε是用来避免零分割的计算机中很小的常数，meanj代表整个种群中第j维的平均位置.

3） 飞行行为

因捕食者的威胁、觅食或其他原因，鸟类将会飞向另一个区域重新觅食.一些鸟作为生产者来寻找食物，另一些则根据这些生产者找到的食物信息来寻找食物，规则4可以区分出鸟类生产者和乞食者，用数学公式表示如下

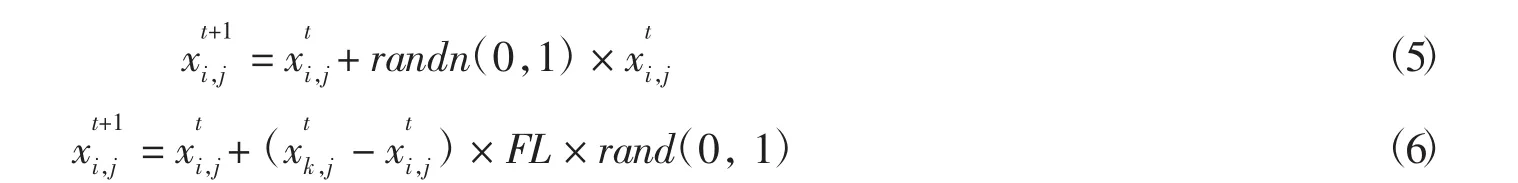
式中：randn（0，1）代表服从均值为0，标准差为1的Gaussian中的一个随机数，k∈ [1，2，3，…，N]，k≠i，FL（FL∈[0，1]）表示乞食者会跟随生产者寻找食物的概率.FQ（FQ>0）为每只鸟飞往另一区域的时间间隔.

2 基于Levy飞行策略的自适应改进鸟群算法

2.1 基于Levy飞行行为的改进策略

“Levy飞行策略”是生物在未知环境中寻找食物的理想方法，在500次Levy飞行中随机步长分布图如图1所示，利用Levy飞行中频繁的短距离搜索可在当前最优解周围仔细搜寻以提高局部搜索能力，利用偶尔长距离的跳跃式搜索可扩增搜索范围增强全局搜索，防止陷入局部最优解[11].Levy飞行策略已成功应用于布谷鸟算法[12]、蝙蝠算法[11]、FOA算法[13]、PSO算法[14]等仿生学智能算法的改进中，并取得了良好的优化效果.鉴于以上Levy飞行策略的优点和实例验证，将其应用于BSA算法中，利用上述随机游走模式初始化鸟群空间的位置，以此扩大搜索范围，增加种群的多样性，跳出局部最优值，较好的平衡BSA算法的全局和局部搜索能力.

采用Mantegna算法得出的Levy飞行路径表达式如下

式中：r1（1，d）、r2（1，d）为[0，1]间的服从标准正态分布的随机数；Levy（λ）为随机步长；λ为幂次数；此处β=1.5.

初始化鸟群的空间位置公式如下

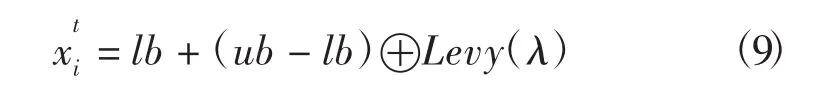
式中：xti为第i只鸟在t时刻的空间位置；ub、lb分别为每只鸟的搜索范围限值；d为搜索维度；⊕代表矢量运算；Levy（λ）为步长服从Levy分布的随机搜索向量.

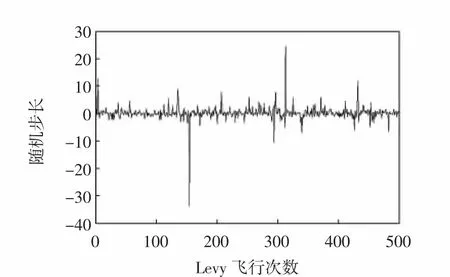
图1 Levy飞行随机步长分布图Fig.1 Levy flight random step size distribution

2.2 （0，1）随机均匀分布自适应改进惯性权重

BSA算法中鸟类觅食行为公式（1）类似于PSO算法中粒子的速度更新公式，故惯性权重w也是BSA算法的重要改进参数，通过设置w可以改变上一时刻觅食位置对当前时刻位置的影响.若利用传统的线性微分递减策略[15]，当在鸟群搜索前期找到最优值，则需要很大的w来快速收敛于此，此时递减的w便降低了收敛速度，若在搜索后期才找到最优值，此时w和鸟类飞行速度均很小，BSA算法易陷入局部最优值.

为了解决上述问题，本文借鉴复杂适应系统理论（CAS）中的自适应性和个体与种群的协同进化作用，采用（0，1）随机均匀分布策略[16]替换线性微分递减策略，从而w可以在迭代初期和后期均可得到较大的值，以此平衡BSA算法的全局与局部搜索能力，提高全局搜索效果.伪代码如下

for i=1：M；%M为最大迭代次数

if个体最优值==全局最优值；

w=0.4+0.5*rand（）；

else

w=0+0.9*rand（）；

end

end

2.3 线性调整学习系数

BSA算法中C和S分别代表认知和社会系数，类似于PSO算法中的自身和社会学习因子，通过自适应调整自身认知经验和社会经验，使鸟群搜索觅食前期C取较大值S取较小值，增加认知经验的比重，增强鸟类的全局搜索能力，搜寻觅食后期C取较小值，S取较大值，增加搜寻食物的社会经验比重，使得局部搜索能力增强，线性调整的学习系数更新公式为

式中：Ce=Ss=0.5，Cs=Se=2.5.

改进后的觅食公式为

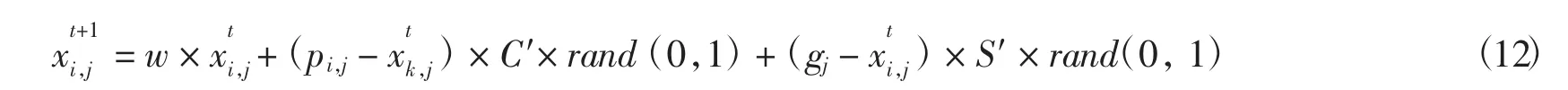
综上，本文利用Levy飞行行为初始化鸟群所在的空间位置，采用（0，1）随机均匀分布自适应改变惯性权重，同时采用线性调整策略改进认知和社会系数，称这种算法为基于Levy飞行策略的自适应改进鸟群算法（LSABSA）.

3 实验仿真与分析

为验证LSABSA算法的改进效果，本文以10个典型Benchmark函数为例，采用MATLAB R2014a编写了相关程序，并对LSABSA算法与PSO、GPSO和BSA算法的仿真实验结果进行了对比验证.

3.1 基本测试函数与实验参数的设置

本文测试函数如表1所示，Sphere、Quadric、Rosenbrock为单模态函数，Rastrigin、Schaffers、Ackley等剩余函数为包含局部极值的多模态函数.具体实验参数设置如下

1） PSO算法

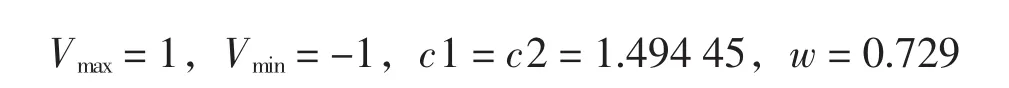
2） GPSO算法

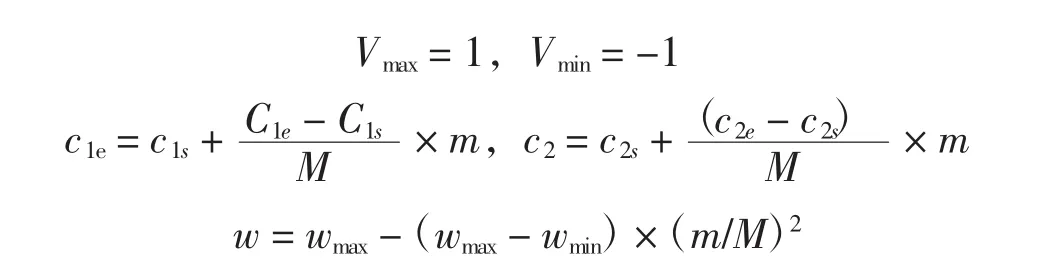
其中：c1e=c2s=0.5，c1s=c2e=2.5，wmax=0.9，wmix=0.4，m为当前迭代次数，M为最大迭代次数，与此同时GPSO算法中加入了自适应变异来增加种群的多样性.

3） BSA算法

LSABSA算法的实验参数设置如式（7） ～式（12） 所示.PSO、GPSO、BSA和LSABSA算法的种群规模均为50，最大迭代次数均为1 000.

表1 典型的Benchmark函数Tab.1 Typical Benchmark function

3.2 测试函数的仿真结果与分析

在PSO、GPSO、BSA和LSABSA4种智能优化算法下，对10个测试函数分别独立寻优运行20次，相应的最优值、最差值、平均值和标准方差数据如表2所示，其最优个体适应度值收敛特性曲线如图2所示.

从表2中可得出如下结论：

1）除病态函数Rosenbrock以外，LSABSA算法比其他算法在所有优化函数上的最优值、最差值、平均值和标准方差都要小，即收敛精度要高稳定性要强，且优化Rosenbrock函数时LSABSA算法性能略低于其他算法.尤其在解决Sphere、Quadric、Ackley和Schaffers函数时LSABSA算法的改进效果十分明显，说明了LSABSA算法改进后的有效性.

2） PSO和 GPSO算法在解决 Quadric、Rastrigin、Ackley、Needle-in-a-haystack、Leung&Wang和Periodic函数优化问题时易陷入局部最优解，PSO算法在解决Sphere和Griewank函数以及BSA算法在解决Ackley函数时也易陷入局部最优解，但此时BSA算法均小于PSO和GPSO算法的均值和和标准方差，而BSA和LSABSA算法在优化Rastrigin、Griewank函数时的最优值、最差值、平均值和标准方差相同，即此时两种算法有相同的收敛稳定性和精确度.总体上，LSABSA和BSA算法明显比其他算法性能优越，除Rosenbrock函数外，LSABSA算法在优化其他函数时的均值和方差也均优于BSA算法，即验证了加入Levy飞行策略增加了种群的多样性，不至于陷入局部最优.

图2表示了4种算法有关准确性和收敛速度的最优个体适应度值曲线，由图易得：Sphere、Quadric、Rastrigin、Ackley、Griewank、Needle-in-a-haystack和Schaffers函数在优化过程中运用LSABSA算法相对于其他算法的收敛速度和收敛精度明显提高，能在极短迭代次数下接近于收敛，且BSA算法收敛效果仅次于LSABSA算法.PSO算法收敛效果最差，在处理Rastrigin和Ackley函数时PSO算法易陷入局部最优解.以上说明采用（0，1）随机均匀分布自适应改进惯性权重以及线性调整学习系数的方法，增强了与外界的适应能力，从而提高了收敛速度和精度.

基于表2和图2的对比结果，整体上来讲LSABSA算法的全局寻优性能、收敛速度、求解精度和稳定性均优于BSA、PSO和GPSO算法，验证了所提算法的优越性.

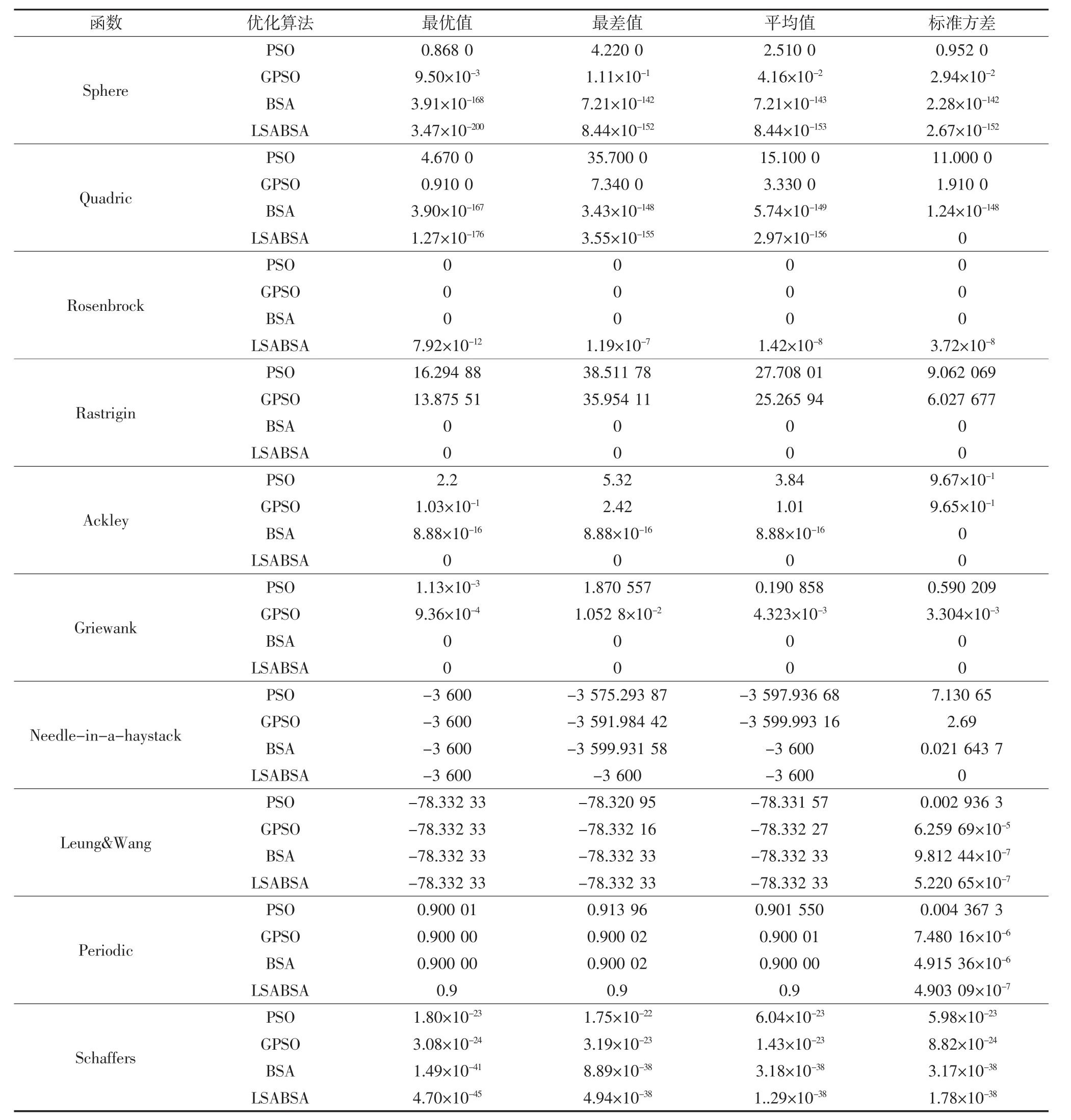
表2 PSO、GPSO、BSA和LSABSA算法对比结果Tab.2 Comparison of PSO，GPSO，BSA and LSABSA algorithm

图2 PSO、GPSO、BSA和LSABSA算法的收敛曲线图Fig.2 The convergence curve of PSO，GPSO，BSA and LSABSA algorithm

4 结论

针对新型仿生学群智能算法-鸟群算法在进化初期种群多样性不足以及在求解部分复杂高维多极值问题时，易出现局部收敛和早熟的问题，引入Levy飞行策略增加种群的多样性，扩大鸟群的搜索空间，采用（0，1）随机均匀分布自适应改进惯性权重和线性调整学习因子策略来平衡全局搜索和局部搜索、提高收敛性能.通过10个典型测试函数的仿真数据结果和收敛特性曲线可得：无论是单模态还是多模态函数，从整体上看，LSABSA算法的效果优于PSO、GPSO和BSA算法，其改进策略提高了算法的全局搜索能力和搜索精度，以此验证了该算法具有较好的收敛速度、求解精度和稳定性.

[1]Das S，Suganthan P N.Differential evolution：a survey of the state-of-the-art[J].IEEE Transactions on Evolutionary Computation，2011，15（1）：4-31.

[2] Jordehi A R，Jasni J.Parameter selection in particle swarm optimisation：a survey[J].Journal of Experimental&Theoretical Artificial Intelligence，2013，25（4）：527-542.

[3] Gao X Z，Wu Y，Kai Z，et al.A knowledge-based artificial fish-swarm algorithm[C]//IEEE，International Conference on Computational Science and Engineering.IEEE，2010：327-332.

[4] Pan W T，Pan W T.A new fruit fly optimization algorithm：taking the financial distress model as an example[J].Knowledge-Based Systems，2012，26（2）：69-74.

[5] Meng X，Liu Y，Gao X，et al.A new bio-inspired algorithm：chicken swarm optimization[M].Advances in Swarm Intelligence.Springer International Publishing，2014：86-94.

[6] Smith K L，Zielinksi S.The startling intelligence of the common chicken[J].Scientific American，2014，2（2）.

[7] Meng X B，Gao X Z，Lu L，et al.A new bio-inspired optimisation algorithm：bird swarm algorithm[J].Journal of Experimental&Theoretical Artificial Intelligence，2016，28（4）：673-687.

[8] 曾嶒，彭春华，王奎，等.基于鸟群算法的微电网多目标运行优化[J].电力系统保护与控制，2016，44（13）：117-122.

[9] 崔东文，金波.改进鸟群算法及其在梯级水库优化调度中的应用[J].三峡大学学报（自然科学版），2016，38（6）：7-14.

[10]崔东文，金波.鸟群算法-投影寻踪回归模型在多元变量年径流预测中的应用[J].人民珠江，2016,37（11）：26-30.

[11]刘长平，叶春明.具有Lévy飞行特征的蝙蝠算法[J].智能系统学报，2013（3）：240-246.

[12]Yang X S，Deb S.Engineering optimisation by cuckoo search[J].International Journal of Mathematical Modelling&Numerical Optimisation，2010，1（4）：330-343.

[13]张前图，房立清，赵玉龙.具有Levy飞行特征的双子群果蝇优化算法[J].计算机应用，2015，35（5）：1348-1352.

[14]付强，葛洪伟，苏树智.引入萤火虫行为和Levy飞行的粒子群优化算法[J].计算机应用，2016，36（12）：3298-3302.

[15]梅真.基于改进粒子群算法的微电网优化运行策略研究[D].武汉：湖北工业大学，2015.

[16]刘举胜，何建佳，李鹏飞.基于CAS理论的改进PSO算法[J].计算机工程与应用，2017，53（5）：57-63.

Adaptive improved bird swarm algorithm based on Levy flight strategy

YANG Wenrong,MA Xiaoyan,BIAN Xinlei

（State Key Laboratry of Reliability and Intelligence of Electrical Equipment,Hebei University of Technology,Tianjin 300130,China）

The new type of biological heuristic swarm intelligence algorithm-the bird swarm algorithm (BSA)suffers from poor population convergence precision，large convergence iteration number and even convergence earlier and be in local optimal problems due to the population diversity deficiency in early evolution and the change of cognitive and group behavioral adjustment parameters.To solve these problems,a levy adaptive improved bird swarm algorithm (LSABSA)is proposed.The random walk model of Levy flight strategy is used to increase the diversity of population and jump out of local optimal value,and by means of(0,1)random uniform distribution adaptive modified the inertia weight and linear adjustment of cognitive and social coefficients to balance the global and local search ability of BSA algorithm,and then improve the accuracy of the algorithm.Finally,10 typical test functions are used to simulate and compare the LSABSA algorithm,particle swarm optimization(PSO)algorithm,improved particle swarm optimization(GPSO)algorithm and BSA algorithm,and the result shows the convergence speed,accuracy and stability of LSABSA algorithm are better than other algorithms.

bird swarm algorithm;Levy flight;(0,1)random uniform distribution;linear adjustment;simulation test

TP18

A

1007-2373（2017） 05-0010-08

10.14081/j.cnki.hgdxb.2017.05.002

2017-04-21

河北省自然科学基金（E2015202241）

杨文荣（1969-），女，教授，博士.

[责任编辑 代俊秋]