永磁同步电机系统神经网络逆解耦控制

刘欣欢，徐桂芝，刘 旭

（河北工业大学 电气工程学院，天津 300132）

永磁同步电机系统神经网络逆解耦控制

刘欣欢，徐桂芝，刘 旭

（河北工业大学 电气工程学院，天津 300132）

提出了一种应用于全速域范围内的表贴式永磁同步电机神经网络逆解耦控制策略，该策略能够实现电机的精确解耦控制以及良好的动静态性能.在证明电机系统可逆性的基础上，对全速域范围内的线性化解耦控制特性进行了分析，针对逆解耦控制策略过于依赖系统数学模型的缺点，提出神经网络逆解耦控制策略，并设计了基于滑模变结构的附加转速与电流控制器.以一台5.2 kW永磁同步电机为被控对象进行仿真以及实验研究，结果表明，此策略能够在全速域范围内实现电机良好的解耦控制，并能够获得较好的动静态性能.

永磁同步电机；神经网络；逆系统；解耦控制；滑模控制

0 引言

永磁同步电机具有体积小、损耗小、可靠性高、效率高、功率因数高、性能优良等优点，在电动汽车、数控机床等领域得到了广泛的应用[1].随着工业化进程的加速，对PMSM系统的要求不再局限于额定工况，而是希望电机能够在基速以下和基速以上全速域范围内运行.目前，将弱磁控制和过调制策略相结合是实现电机基速以上运行的有效方法[2-3].

弱磁控制是通过增大定子直轴去磁电流，利用直轴电枢反应削弱电机的气隙磁场，进而等效的减弱励磁磁场来达到弱磁增速的目的.过调制通过增加逆变器输出的基波电压幅值，增大直流母线电压的利用率，从而达到扩大电机调速范围的目的.

解耦控制是实现永磁同步电机系统高性能静态特性和动态特性的关键，经常使用的解耦控制包括直接转矩控制、矢量控制以及逆系统线性化解耦控制等[4].矢量控制和直接转矩控制对电机的模型参数依赖性较强，在负载扰动和电机参数变化时很难实现电机系统的良好的解耦特性.

逆系统解耦控制方法是通过构造逆系统，将被控对象补偿为具有线性传递关系的系统，具有直观形象，易于理解的优点.但由于逆系统的构建在很大程度上依赖被控电机的数学模型以及模型中电机的参数，因此该方法存在一定的局限性.文献 [5]应用逆系统方法对永磁同步电机进行解耦控制研究，能够实现电机转速和转矩的基本解耦，但是当电机启动和负载突变时系统的动态性能不佳.

神经网络具有很强的容错性、鲁棒性和非线性映射能力，能够逼近任意非线性函数，将神经网络引入逆系统解耦控制中，能够兼顾两者的优点，实现系统的精确解耦以及高性能控制.文献 [6]中应用基于神经网络的逆系统解耦控制方法对感应电机进行控制，即通过静态神经网络以及积分器一起来逼近电机逆系统，并与原系统串联组成伪线性系统，从而使用线性控制方法对感应电机进行控制，该控制策略对模型参数的变化及负载扰动有较强的鲁棒性.文献 [7]将神经网络逆控制策略应用于无刷直流电机中，该方法对负载扰动与电机参数摄动有较强的鲁棒性.

本文将神经网络逆解耦控制策略应用于永磁同步电机系统，将电机系统动态解耦为二阶转速子系统和一阶电流子系统，以实现永磁同步电机系统的精确解耦以及高性能控制.同时设计了滑模附加转速与电流控制器，结合神经网络逆系统构成复合控制器，实现电机系统基速以下和基速以上全速域范围内的控制，并通过仿真和实验结果验证了本文所提策略的有效性.

1 永磁同步电机的模型及其可逆性分析

1.1 永磁同步电机弱磁过调制控制

基速以下时，表贴式永磁同步电机转速和转矩的关系为[8]

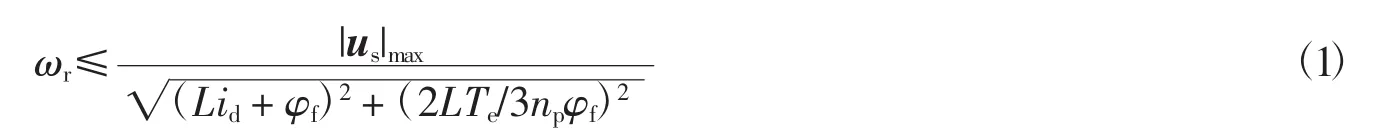
通过式（1）可知，电机运行于基速以上状态时，要提高电机的转速需要采用弱磁控制或者过调制控制方法.弱磁控制方法采用电压外环反馈补偿控制策略.基速以下运行时，采用id=0的控制方法；基速以上运行时，当电机的端电压大于逆变器的电压极限值时，需要通过增大定子直轴去磁电流，从而削弱气隙磁场，即弱磁控制的方法来扩大电机的调速范围.

如图1所示为空间矢量调制策略（Space Vector Pulse Width Modulation，SVPWM） 过调制区域示意图.图中六边形内切圆为采用正弦SVPWM调制策略时输出的电压矢量范围，为增加逆变器输出的基波电压幅值，需要采用SVPWM过调制策略，即将输出的电压矢量范围从内切圆扩大至六边形上，从而达到扩大电机调速范围的目的.

图1中电压矢量U0至U7分别为两电平逆变器输出的8个电压矢量，其中U1至U6为非零电压矢量，U0和U7为零电压矢量.图中的斜线区域对应的是过调制1区，当参考电压矢量Ur的轨迹位于此区域时，保持矢量相位不变，对应的矢量幅值缩减至图中由粗黑线围成的六边形上；外面的位于六边形和圆之间的I至VI区域对应过调制2区，当参考电压矢量Ur的轨迹位于此区域时，逆变器输出的电压矢量分别为U1至U6.

1.2 数学模型及可逆性分析

假设PMSM磁路未饱和，粘滞摩擦系数B=0，忽略磁滞损耗和涡流损耗，表贴式永磁同步电机在两相旋转坐标系下的微分方程为

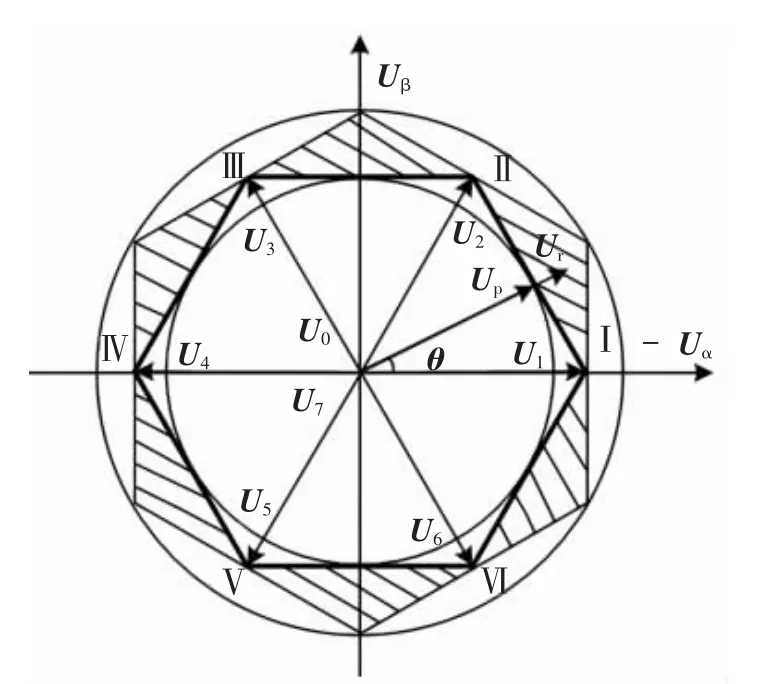
图1SVPWM过调制区域示意图Fig.1 Over-modulation region of PMSM

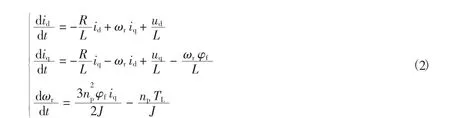
式中：ud、uq分别为定子电压的d轴和q轴分量；id、iq分别为定子电流的d轴和q轴分量；R为定子电阻；J为转动惯量；TL为负载转矩.

在基速以下时，采取id=0的控制方式；在基速以上时，采取id＜0的控制方式.因此为了实现全速域范围内的控制，本文选取定子直轴电流id和电机电角速度ωr作为系统的输出，那么系统的输出变量、状态变量、输入变量分别如下

永磁同步电机系统可以等价为一个两输入两输出的三阶非线性系统，采用Interactor算法对该系统进行可逆性证明.

系统的状态方程、输出方程分别为

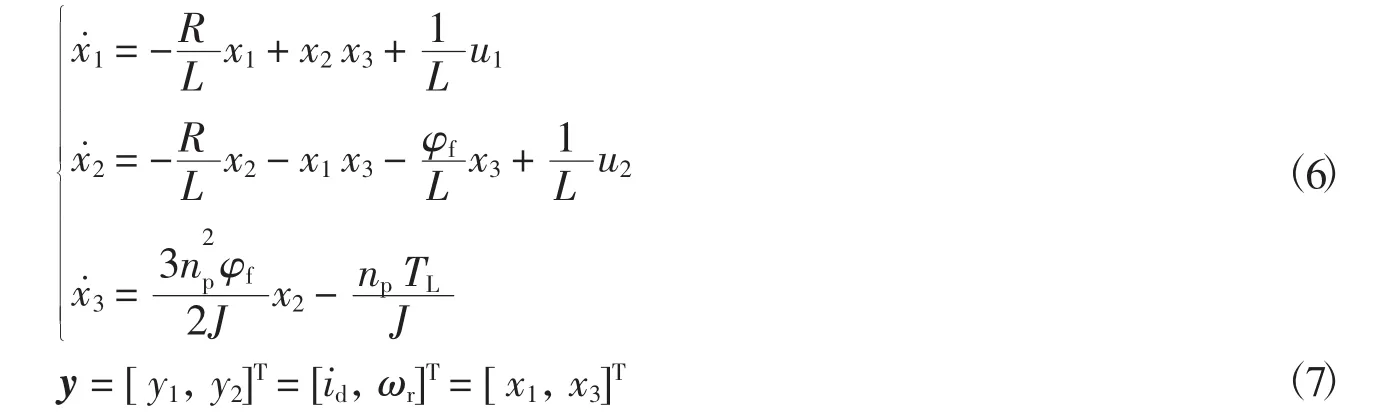
对系统的输出变量y不断进行求导，直至其导数中出现输入变量u，求导停止，下面先对y1求时间的导数

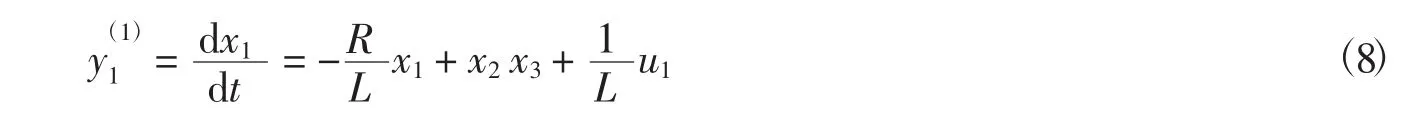
由式（8）可以看出，y1的一阶导数已经出现了u.使Y1=y（11），此时可以求得Y1对u的雅克比矩阵为

式（9）中雅克比矩阵的秩为1，即该矩阵满秩，即α1=rank（∂Y1/∂u）=1，接着对y2求时间的导数，其一阶导数为

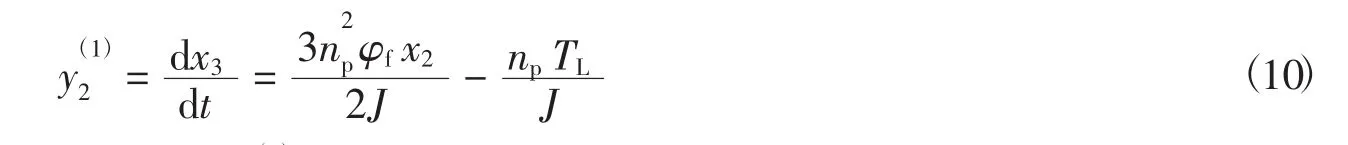
由式（10）可以看出 y（21）中没有出现u，因此对y（21）求时间的导数，如式（11）所示

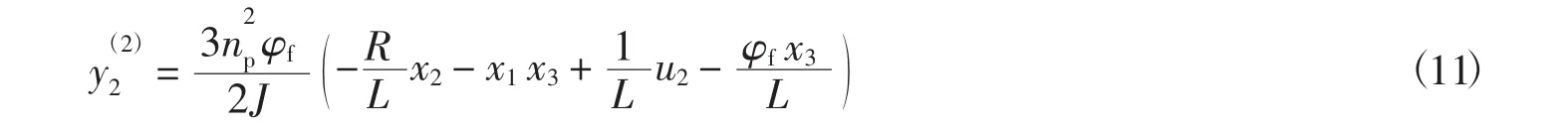
由式（11）可以看出，y2的二阶导数此时可以求得Y2对u的雅克比矩阵为

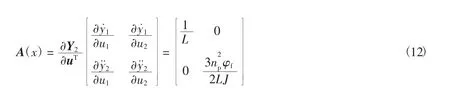
式（12）中雅克比矩阵的秩为2，即该矩阵满秩，即α2=rank[A（x）]=2.其矢量相对阶：α=[α1，α2]T=[1，2]T，存在如下关系式α1+α2=3=n，式中n表示x的维数，由此可知永磁同步电机系统不存在隐动态.经以上证明，PMSM系统是可逆的.

可求得表贴式永磁同步电机逆系统的解析表达式为

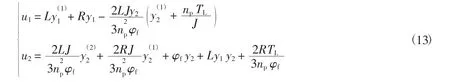
所以逆系统可表示为

根据线性控制理论，对式（13）描述的系统进行闭环控制，电流子系统属于一阶系统，可采用PI控制器；转速子系统属于二阶系统，可采用PD控制器.

1.3 过调制策略下系统的可逆性分析

当电机运行于基速以上时，需采用过调制策略来扩大电机的调速范围，此时将永磁同步电机和逆变器看做一个整体，并忽略逆变器的时滞，分析此时系统的可逆性.

由图1可知，永磁同步电机的d、q轴的实际电压值与给定d、q轴电压值的数学关系式为

式中：u*d、u*q分别为逆变器d轴和q轴给定电压；k为满足关系式k≤1的常数.当参考电压矢量位于图1中黑色六边形内部时，k=1；当参考电压矢量位于由粗黑线围成的六边形外部时，k＜1.将式（15）和式（16） 代入式 （2），可以得到

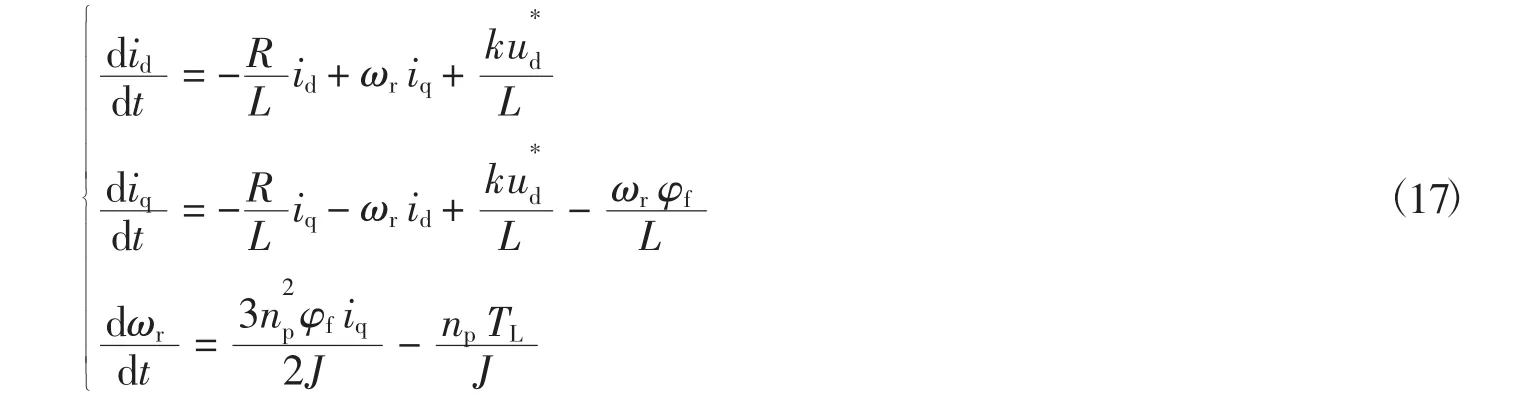
基于逆系统的永磁同步电机系统线性化解耦控制框图如图2所示.

2 永磁同步电机系统神经网络逆解耦控制

2.1 逆系统解耦控制策略解耦特性分析

电机在基速以下运行时，忽略电机铁心损耗、磁路饱和等因素条件下，逆系统的解析表达式如式（13），此时解析逆系统与电机系统组成的伪线性系统是线性的，此时整个控制系统可以获得较好的动静态性能.

图2 基于逆系统的PMSM系统线性化解耦控制框图Fig.2 Block decoupling control scheme of PMSM system based on inverse system

电机在基速以上过调制策略下运行时，k=|Up|/Ur|，系数k的取值是一个与参考矢量Ur的幅值大小和相位有关的非线性函数，可知在弱磁过调制工况下增大了系统的非线性程度以及耦合性.

逆系统方法依赖于非线性系统的精确数学模型和逆系统的解析表达式，因此存在电机参数变化的鲁棒性和适应性不理想，抗负载扰动能力不强等缺点.

2.2 控制系统框图

图3为基于复合控制的永磁同步电机系统框图.图中的灰色阴影区域分别表示附加滑模控制器、神经网络逆系统、弱磁控制器以及SVPWM过调制模块，虚线框内为由附加滑模控制器和神经网络逆系统构成的复合控制器.

2.3 神经网络逆系统的构建

神经网络逆系统由静态神经网络和积分器两部分构成，分别表征神经网络逆系统的静态特性和动态特性，从而实现动态神经网络的功能.将神经网络逆系统和永磁同步电机原系统串联起来可以得到两个独立的伪线性子系统，包括具有二阶线性积分关系的转速子系统与具有一阶线性积分关系的电流子系统.神经网络逆系统的基本结构如图4所示.

用于逼近未知非线性函数的静态神经网络选用3层BP神经网络，节点数分别选为：输入节点6个，输出节点2个，隐含节点通常选为输入节点的两倍，经过仿真设为12个.输入向量为 [id，id′，ωr，ωr′，ωr″，TL]T，输出向量为[ud，uq]T，选取的隐含层神经元的激励函数为双曲正切函数，输出层神经元的的激励函数为线性阈值函数.

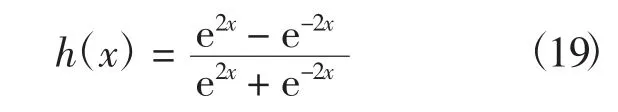
本文所用的静态神经网络采用离线训练的方法来获取，首先需要进行输入输出数据的采集，采用以PID附加控制器的PMSM解析逆系统来对本文所需数据进行采集，进行数据采集的PMSM系统结构图如图5所示.

为了保证神经网络有较好的泛化能力，应该选取足够的激励信号作为解析逆系统的输入信号，转速和电流的给定值应取覆盖电机的整个工作区域的随机量，本文仿真中转速给定信号和电流给定信号为范围分别为0～80 r/min、-10～1A的随机方波信号，每一个转速给定信号与电流给定信号持续时间为1s，采样频率为10kHz，以保证数据中包含足够的稳态与瞬态信息，信号平滑滤波后闭环采集数据 {id，id′，ωr，ωr′，ωr″，TL} 和{ud，uq}. 然后对获得的数据进行归一化处理，其中的2/3的数据作为训练样本集，剩下1/3的数据作为检验样本集，用来检验模型的泛化能力.为加快神经网络的训练速度，本文采用带动量项和变学习速率的改进型BP算法对神经网络进行训练，直到取得满意的精度为止.

转速环采用PD控制，含有微分环节，考虑到微分项会在实验过程中引进噪声，并且在本文实验平台下，程序中控制周期较大为 100 μs，会造成微分项 ωr′的计算不准确.在忽略电机摩擦系数时，注意到电机的转矩和转速加速度之间存在如式（20）所示的关系式，转速的一阶导数ωr′可以通过式（20） 求得.

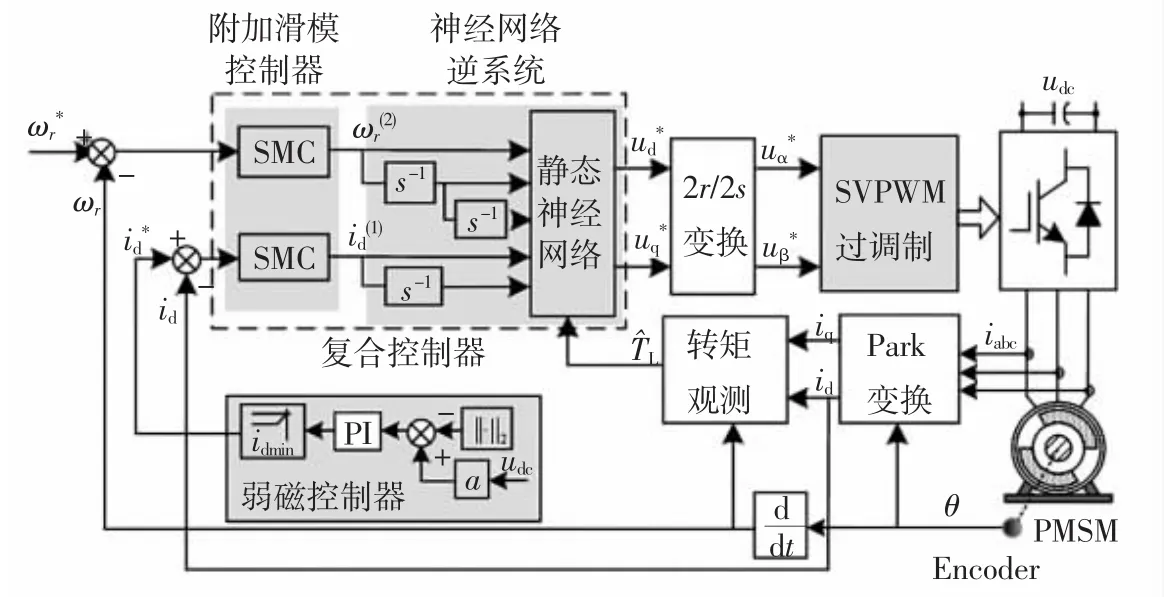
图3 基于复合控制的PMSM系统框图Fig.3 Block diagram of PMSM system based on compound control

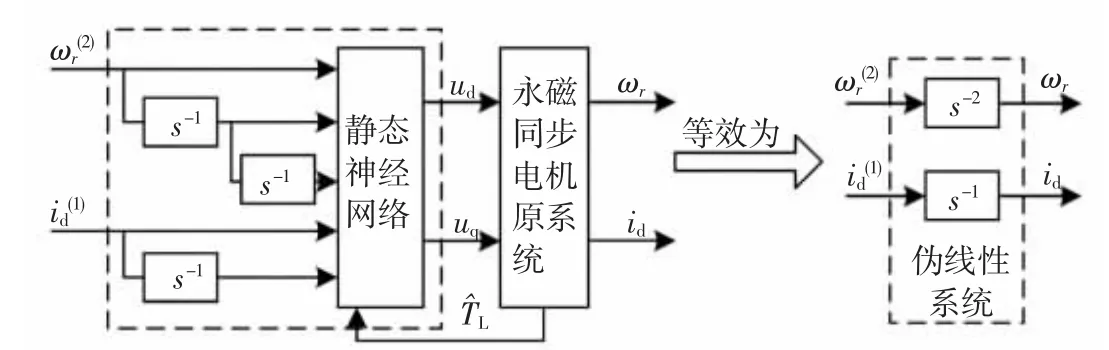
图4 神经网络逆系统的基本结构Fig.4 Radical structure of neural network inverse system

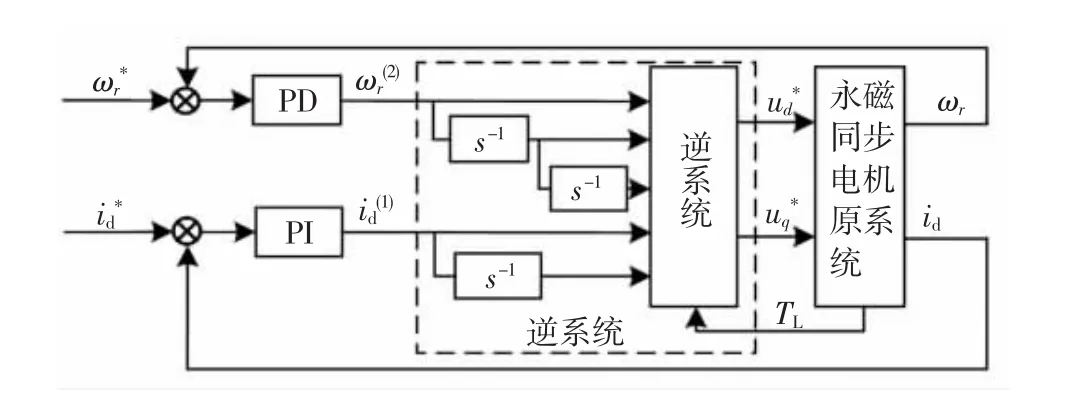
图5 神经网络训练数据采集的逆系统控制结构图Fig.5 Inverse system control structure diagram of the neural network training data acquisition

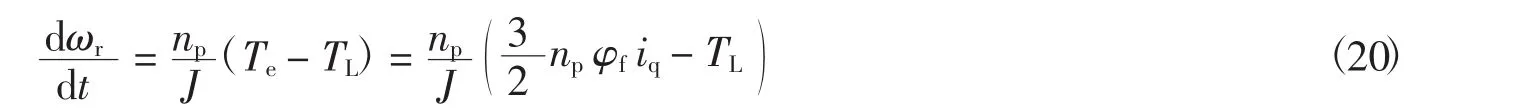
2.4 附加滑模控制器的设计

滑模变结构控制具有算法简单、响应速度快以及鲁棒性强等优点，被广泛的应用于电机系统控制领域当中.本文设计了基于滑模变结构的附加转速与附加电流控制器对电机系统进行闭环控制，来提高系统的动静态性能.

本文设计了基于新型指数趋近律的滑模变结构附加控制器来分别对二阶转速子系统和一阶电流子系统进行闭环控制.本文在常规指数趋近律的基础上，提出了一种新型指数趋近律

其中，ε、k都是大于零的常数，因此满足稳定性条件，即在新趋近律滑模控制下系统是稳定的.

考虑到系统的快速性以及稳态误差，这里设计k为转速误差绝对值的非线性函数，如图6所示为变k流程图，图中x1为速度误差绝对值；ni为给定的比较值，n1＜n2＜…＜ni；ki为通过比较后选择的值，相应的有k0＜k1＜…＜ki.

对电流环进行设计，选取系统状态变量为

2.5 转矩观测器的设计

在静态神经网络的输入 {id，id′，ωr，ωr′，ωr″，TL}和上文中转速一阶导数的计算中均用到了转矩的值，因此需要对负载转矩进行观测.本文采用负载转矩滑模观测器对负载转矩进行观测.

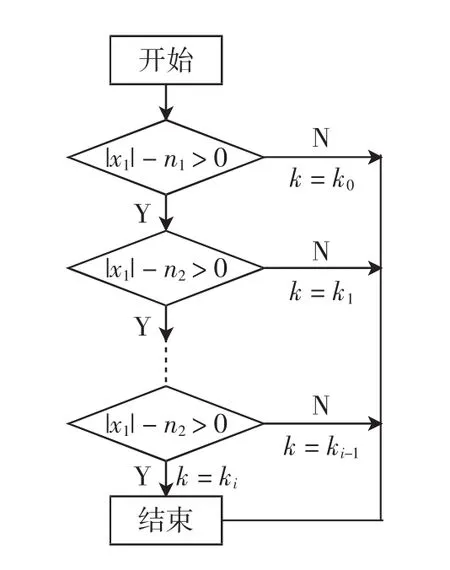
图6 变k流程图Fig.6 The flow chart of the variable k

忽略摩擦系数，将TL作为PMSM系统的扩展状态变量，可构建得到永磁同步电机状态方程为

由于系统的控制周期较小，可以假设在一个控制周期内负载转矩是不变的，即T˙L=0，那么建立永磁同步电机系统的滑模状态观测器如下

式中：U=k sgn（ωˆr-ωr），k、g均为常数，分别为滑模和反馈增益；TˆL、ωˆr分别为负载转矩和电角速度的估计值，将上述两式作差，可知滑模观测器的误差方程为

式中：e1=ωˆr-ωr为电机转速的估计误差；e2=TˆL-TL为负载转矩的估计误差.定义滑模面s=e1=ωˆr-ωr，根据广义滑模条件的可达条件ss˙≤0可得

在滑动模态时存在关系式s=s˙=0，此时式（34）可化简为

根据式（36）可以求出负载转矩误差方程为

式中，c为常数，系统的稳定性条件为-gnp/J＞0，即g＜0，系统的趋近速度由反馈增益g来决定.图7为负载转矩滑模观测器的结构框图.

由图7观测得到的电机的负载转矩作为神经网络的输入量，图中观测得到的转速的一阶导数作为上述附加转速滑模控制器的输入.

3 仿真分析

本节采用Matlab/Simulink平台对基速以下和基速以上两种工况下的神经网络逆解耦控制进行了仿真分析.给定直流母线电压值为450 V，仿真所用的永磁同步电机参数如表1所示.

本文中负载转矩给定最大值为150 Nm，选取转矩为150 Nm时电机能达到的最大转速为基速，根据式（1）可求得基速为n0=63.3 r/min.电机在空载运行状态的最高转速为63.4 r/min，为了保证PMSM运行于弱磁过调制区，在基速以上工况下的仿真中转速给定值为70 r/min.

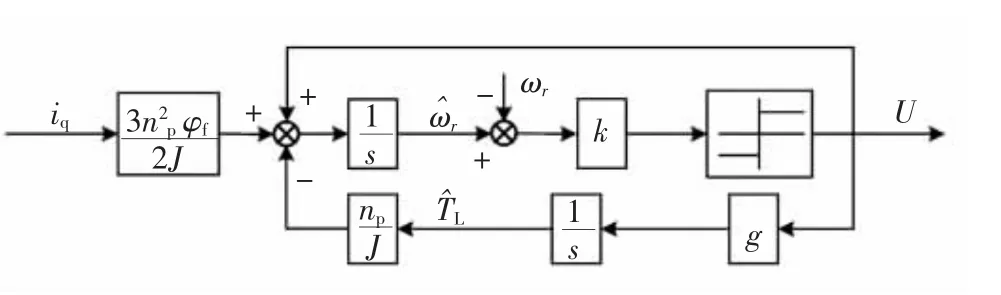
图7 负载转矩滑模观测器的结构框图Fig.7 The structure diagram of load torque sliding mode observer

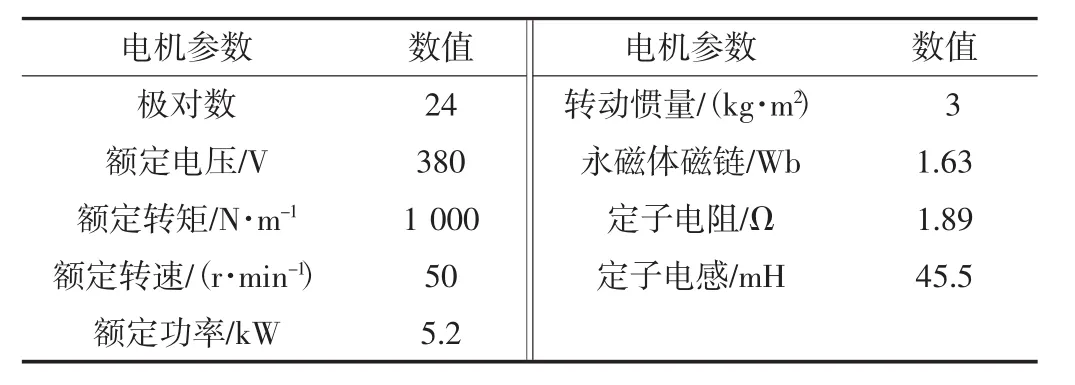
表1 电机参数Tab.1 Parameters of The Tested motor

基速以下的仿真中，电机参考转速为30 r/min，启动时电机负载为0 N·m，后突变为150 N·m.图8给出了基速以下时逆系统解耦控制和神经网络逆解耦控制策略仿真波形对比，图中依次给出了转矩、转速波形.

基速以上的仿真中，电机参考转速为70 r/min，启动时电机负载为0 N·m，后突变为150 N·m.图9给出了基速以上时逆系统解耦控制和神经网络逆解耦控制策略仿真波形对比，图中依次给出了转矩、转速波形.

对比图8a）和图8b），图9a）和图9b） 可以看出，在基速以下和基速以上两种工况下，逆系统解耦控制策略在突加负载过程中，转矩和转速均有较大的抖动，系统的抗负载干扰能力不强，永磁同步电机系统的动态性能不佳.采用神经网络逆解耦控制策略时，突加负载过程中转矩波动很小，转速基本没有变化，系统的动态性能良好，因此神经网络逆解耦控制策略能在全速域范围内有效的改善系统的动态性能.

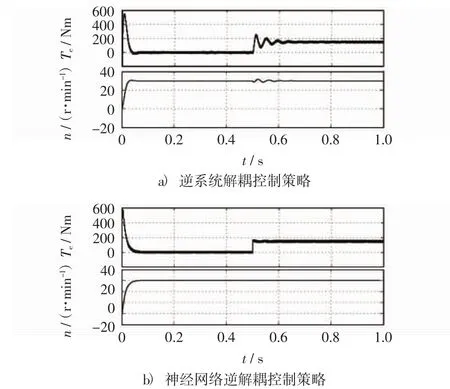
图8 基速以下不同控制策略下系统仿真结果Fig.8 Simulation results of different control strategies below the base speed

4 实验结果

本文采用了一台5.2 kW永磁同步电机，分别在逆系统解耦控制和神经网络逆解耦控制两种控制策略下对电机进行实验，并对实验结果进行了对比分析.控制电路的主控芯片为浮点型TMS320F28335 DSP，协控制芯片为Cycone系列FPGA.系统的采样周期为100 μs，开关频率为5 kHz，实验电机参数如表1所示.

为了分析系统的动态性能，分别对突加负载和转速突变2种情况进行了实验分析.在突加负载的实验中，电机参考转速为30 r/min，启动时电机负载为0 N·m，后突变为150 N·m.图10给出了突加负载时逆系统解耦控制和神经网络逆解耦控制策略下的实验波形对比结果，从上至下依次为转矩、转速波形.

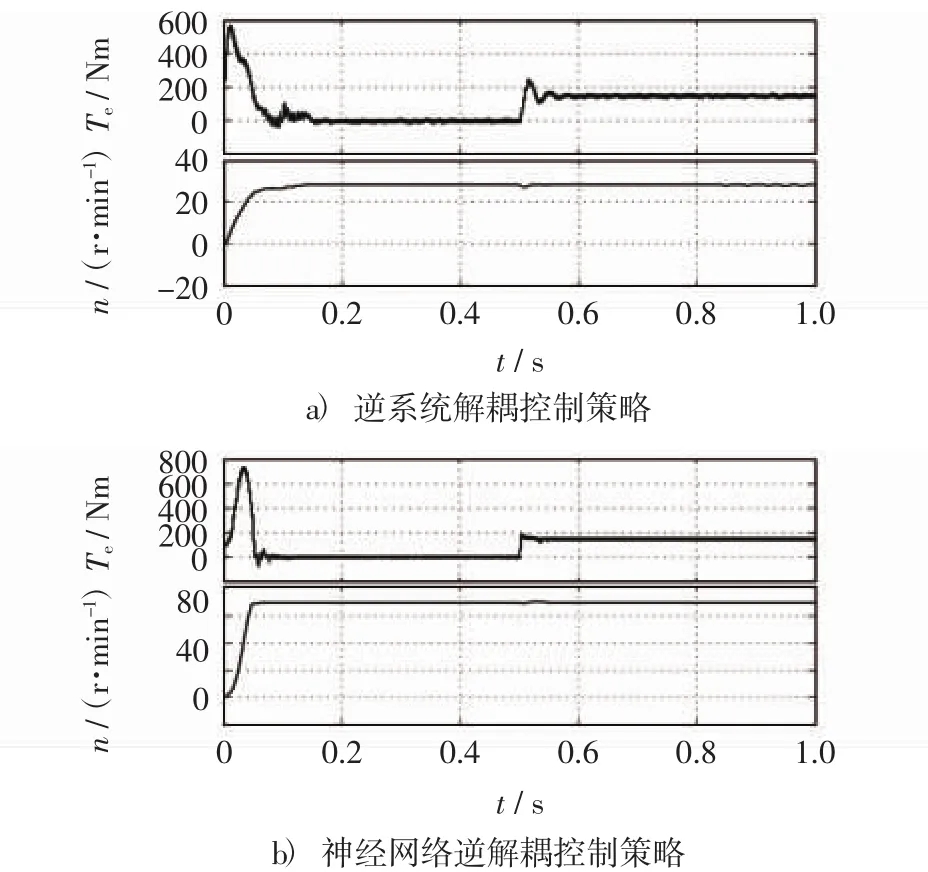
图9 基速以上不同控制策略下系统仿真结果Fig.9 Simulation results of different control strategies above the base speed

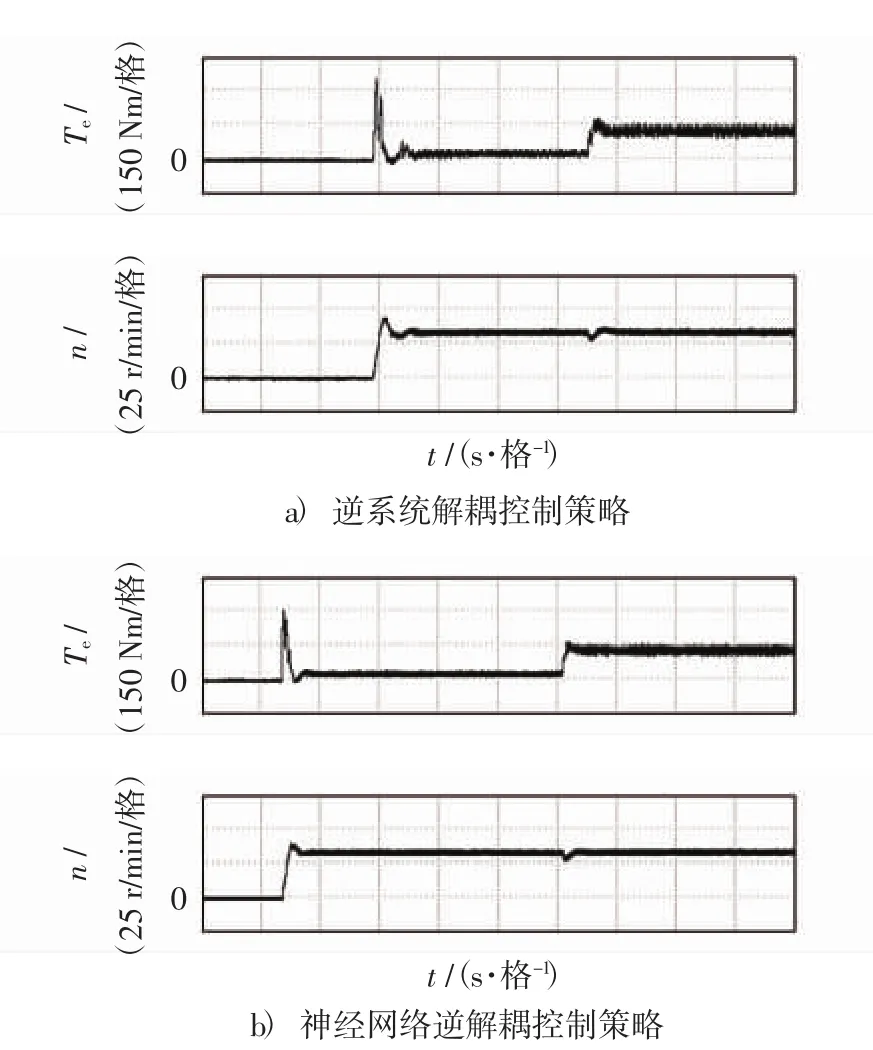
图10 突加负载时不同控制策略下系统实验结果Fig.10 Experiment results of different control strategies under sudden loading

在转速突变的实验中，启动时电机转速给定值为30 r/min，后突变为40 r/min，电机负载转矩初始给定值为150 N·m，由于在本文实验中负载电机定子两端接的是阻感负载，因此在转速突变时负载电机的定子端电压会发生突变，进而电流会变化，负载转矩也会变化.图11给出了转速突变时逆系统解耦控制和神经网络逆解耦控制策略下的实验波形对比结果，从上至下依次为转矩、转速波形.

由图11可以看出，采用逆系统解耦控制策略时，电机在空载启动时系统的转矩和转速抖动较大，在带载启动和转速突变时，转速存在一定的超调，逆系统解耦控制策略可以实现转速和转矩的良好解耦，系统的动态性能较差，但是静态性能良好.而采用神经网络逆解耦控制策略后电机系统的转矩和转速抖动明显减小，动态性能得到了明显的改善.

5 结论

逆系统解耦控制策略具有抗负载干扰能力差、动态性能不佳等缺点.针对这个问题，本文将神经网络逆解耦控制策略应用于全速域范围内的永磁同步电机系统中，并采用滑模附加控制器和神经网络逆系统一起构成复合控制器对永磁同步电机系统进行控制，来提高系统的抗负载干扰能力和动态性能.分别在2种控制策略下采用一台5.2 kW永磁同步电机进行仿真和实验研究.结果表明本文所提策略可以在全速域范围内有效的改善系统的动态性能.

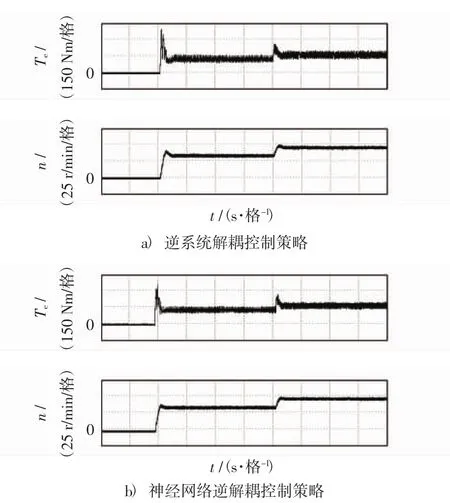
图11 转速突变时不同控制策略下系统实验结果Fig.11 Simulation results of different control strategies under the condition of sudden change of speed

[1] Lin Faa-Jeng，Lin Chih-Hong．A permanent-magnet synchronous motor servo drive using self-constructing fuzzy neural network controller[J]．IEEE Transactions on Energy Conversion，2004，19（1）：66-72．

[2] Kwon Tae-Suk，Sul Seung-Ki．Novel antiwindup of current regulator of a surface-mounted permanent magnet motor for flux-weakening control[J]．IEEE Transactions on Industry Applications，2006，52（5）：1293-1300．

[3] Tripathi A，Khambadkone A M，Panda S K．Torque ripple analysis and dynamic performance of a space vector modulation based control method for AC-drives[J]．IEEE Transactions on Power Electronics，2005，20（2）：485-492．

[4] 周华伟，温旭辉，赵峰，等．基于内模的永磁同步电机滑模电流解耦控制[J]．中国电机工程学报，2012，32（15）：91-99．

[5] 刘刚，李华德，曹勇．基于逆控制的永磁同步电机速度伺服系统[J]．北京科技大学学报，2009，31（4）：511-515．

[6] 戴先中，张兴华，刘国海，等．感应电机的神经网络逆系统线性化解耦控制[J]．中国电机工程学报，2004，24（1）：112-117．

[7] 刘国海，金鹏，魏海峰．无刷直流电机调速系统神经网络逆控制[J]．电工技术学报，2010，25（8）：24-30．

[8] 王贺超，夏长亮，阎彦，等．基于谐振控制的表贴式永磁同步电机弱磁区电流谐波抑制[J]．电工技术学报，2014，29（9）：83-91．

[9] 张晓光，孙力，赵克．基于负载转矩滑模观测的永磁同步电机滑模控制[J]．中国电机工程学报，2012，32（3）：111-116．

Neural network inverse based decoupling control for PMSM drive system

LIU Xinhuan,XU Guizhi,LIU Xu

（School of Electrical Engineering,Hebei University of Technology,Tianjin 300132,China）

This paper presents a neural network inverse based decoupling control strategy for SPMSM(surface permanent magnet synchronous motors)in full speed range.The strategy can achieve good decoupling control performance,and obtain good dynamic and static performance in full speed range.Based on the motor system reversible proof,the linearized decoupling control characteristics are analyzed.Aiming at the disadvantage of the inverse decoupling control strategy which is too dependent on the mathematical model,the neural network inverse based decoupling control strategy is proposed,and an additional speed and current controller based on sliding mode variable structure are designed.A 5.2 kW permanent magnet synchronous motor is used as the controlled object for simulation and experimental study,and the result show that the neural network inverse based decoupling control strategy can achieve good decoupling control performance,and can obtain good dynamic and static performance in full speed range.

permanent magnet synchronous motor;neural network;inverse system;decoupling control;sliding mode control

TM341

A

1007-2373（2017） 05-0001-09

10.14081/j.cnki.hgdxb.2017.05.001

2017-05-03

国家自然科学基金（51507045）

刘欣欢（1989-），男，硕士研究生.

[责任编辑 代俊秋]