汽车悬架系统路面激振模型研究
2017-11-13金锐超
金锐超
(渭南职业技术学院 714000)
汽车悬架系统路面激振模型研究
金锐超
(渭南职业技术学院 714000)
道路不平度是对汽车产生的主要激励,影响汽车行驶的平顺性和舒适性。本文建立了路面空间功率谱数学模型,并将其换算成路面不平度的时间功率谱,对其做傅里叶变换得到了汽车悬架系统分析时常用的路面激励模型。
不平度;路面激励;路面功率谱
1 背景介绍
路面不平度是用来衡量道路起伏程度的参数。道路起伏不平,会对行驶的汽车产生向上的激振力,从而影响汽车的行驶平顺性、舒适性。对汽车悬架进行性能分析不可避免的要用到路面激励,所以研究道路不平度有非常重要的意义[1-2]。
2 模型建立
按照国际标准化组织制定的标准,路面激励不平度的衡量问题采用路面功率谱密度方式表示,该种方式适用于各种路面。路面相对于基准平面的高度q沿道路走向长度I的变化q(I)称为路面纵断面曲线或不平度函数。这个函数的自变量为路面与选定坐标远点的距离I,而不是之间,因此,对应路面激励q(I)的功率谱为Gq(n)。
路面功率谱采用下式作为拟合表达式。

n为空间频率(m-1),表示每米长度中所包含的波的个数,n=1/λ。n0为参考空间频率(n0=0.1m-1)。Gq(n0)为空间参考频率下的路面功率谱密度值,称为路面不平度系数(m2/m-1=m3)。ω为频率指数,为双对数坐标上斜线的斜率,它决定路面功率谱密度的频率结构。
公式1在双对数坐标上为一斜线,对实测路面功率谱拟合时,为了减少误差,在不同空间频率范围内可以选用不同拟合系数,进行分段拟合,但不应超过4段。上述路面功率谱指的是垂直位移功率谱密度,还可以采用不平度函数对纵向长度的一阶倒数速度功率谱密度和二阶导数加速度功率谱密度来补充描述路面不平度的统计特性。
可以看出,路面速度功率谱幅值在整个频率范围内为一个常数,即为一个“白噪声”,幅值大小只与不平度系数有关,用它来计算分析振动响应的功率谱会更方便。路面不平率的功率谱密度为计算要用到时间频率功率谱密度,因此需要将路面空间功率谱换算成路面不平度的时间功率谱。
设汽车速度v(m/s),则时间频率如下。

根据自功率谱密度与相关函数为傅里叶变换对的关系,可得空间频率功率谱密度如下。
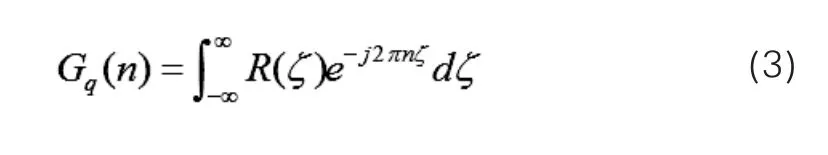
ξ是路面之间两点间的距离,τ为时间间隔,它们之间关系如下。

由公式2、3、4可得

将公式3代入公式5就可以得到空间谱密度与速度的关系。

在这里需要说明的是,公式6所描述的路面激励适合于线性悬架系统模型,对悬架进行频率分析时,可以直接引用该公式。在汽车悬架分析的过程中,不仅在频域进行分析,而且还要在时域进行分析。因此路面激励模型也要有时域模型,这就要求将公式6进行时域计算。
路面起伏所引起的车轮振动输入可以看成一个滤波器,并设该滤波器的模型,将1单位白噪声w(t)输入到该滤波器中,其输出为路面起伏位移。
对于一个线性系统来说,频率响应函数建立后,可以输入振幅功率谱密度求出系统输出变量的功率谱密度,计算过程依据2个法则:第一,输出功率谱等于输入功率谱乘以频率响应函数的平方;第二,输出变量的均方根等于其功率谱密度函数在频域范围内的积分再开方。
当ω=2时,时间频率功率谱密度公式如下。

所以时间频率的速度与频率谱密度的关系式如下。
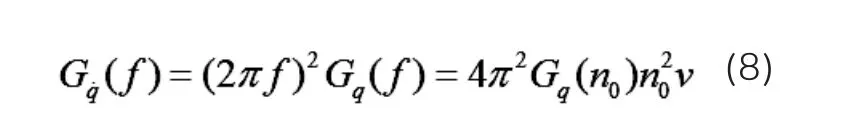
对上式求傅立叶反变换,即可得出路面激励在时域情况下的函数表达式。
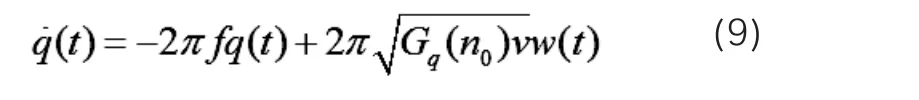
公式中f取0.06~0.07 Hz,Gq(n0)反映了路面的反应状况。各种路面Gq(n0)的取值如表1所示。

表1 各种路面Gq(n0)的取值
公式9便是汽车悬架系统分析时常用的路面激励模型,该模型的路面起伏位移是采用微分形式表示的,所以在使用的时候需要用积分处理,该路面激励表达式也被称作积分白噪声路面激励表达式。
3 结束语
本文从路面激励q(I)的功率谱出发,建立垂直位移功率谱密度数学模型并将其换算成路面不平度的时间功率谱,对其做傅里叶变换得到了汽车悬架系统分析时常用的路面激励模型,为悬架系统的平顺性研究提供激振模型。
[1]段虎明,石峰等.路面不平度研究综述[J].振动与冲击,2009,28(9):33-35.
[2]周长城.汽车液压筒式减振器设计及理论[M].北京:北京大学出版社,2012.110-116.
F407.471文献标示码:A
金锐超,教师,研究方向为汽车NVH特性研究。
