基于优化决策树和EM的缺失数据填充算法*

梁秉毅 蔡延光 蔡颢 戚远航 黄何列 Ole Hejlesen



基于优化决策树和EM的缺失数据填充算法*

梁秉毅1蔡延光2蔡颢2戚远航2黄何列2Ole Hejlesen3

（1.广州市第三公共汽车公司 2.广东工业大学自动化学院 3.奥尔堡大学健康科学与工程系）

针对大数据管理与应用中数据缺失的问题，提出一种基于优化决策树和EM的缺失数据填充算法对多属性缺失数值型数据进行填充。为解决决策树过分拟合问题，该算法采用基于精英策略的自适应遗传算法优化后的决策树对数据进行分类，再结合EM算法实现数值型数据的填充。仿真结果表明：对比优化前的决策树算法，优化后的决策树分类精度更高，平均填充耗时更少。

数据填充；决策树；EM算法；遗传算法

0　引言

数据缺失是数据管理中经常面临的问题，含有缺失数据的多变量数据无法在绝大多数的统计模型中直接分析。当数据库中出现缺失数据时，一般采用数据删除或数据填充的方法。如果缺失数据较少，可直接删除有缺失的记录，但缺失数据较多时，删除大量数据会给研究结果带来一定的误差。因此，数据填充是当前解决数据缺失的主要方法。

近年来，许多学者在数据填充领域进行了深入的研究。李宏等提出一种基于贝叶斯网络和期望最大值法的缺失数据填充算法[1]；武森等提出不完备数据聚类的缺失数据填补方法，并以不完备数据聚类的结果为基础进行缺失数据的填补[2]；张婵提出一种基于支持向量机和回归填充法的缺失数据填充算法[3]；袁景凌等提出一种基于完备相容类的不完备大数据填补算法、一种基于离散弱相关的决策森林并行分类算法和一种增量更新决策森林的算法[4]；李忠波等提出一种新的朴素贝叶斯分类器进行数据填充[5]；Amiri M采用模糊粗糙集进行数据填充[6]；Turrado C C提出一种混合算法解决数据填充问题，并把该算法应用在相关的电力数据中[7]。但这些数据填充算法普遍存在分类精度低、填充耗时长等问题。

因此，本文提出了一种基于优化决策树和EM的缺失数据填充算法，以基于精英策略的自适应遗传算法优化后的决策树和EM算法相结合的方式，解决多属性数值型数据缺失的问题，提高数据填充精度和降低数据填充耗时。

1　优化决策树

1.1　决策树

决策树算法是一种典型的分类算法，构建决策树的思想与贪婪算法类似，采用自顶向下递归的方式[8]。先对原始数据进行处理，得出观察样本；再从训练集和它们相关联的类标号生成可读的规则和决策树。随着树的构建，训练集递归地划分成较小的子集。决策树构建分为5个步骤。

步骤1：采集组数据，作为建立决策树分类器的训练数据集。

步骤2：所有记录看作一个结点，代表训练样本的单个结点开始。

步骤3：遍历每个变量的每一种分割方式，找到最好的分割点。如果样本都在同一个类，则该结点成为树叶，并用该类标记；否则算法选择最有分类能力的属性作为决策树的当前结点。在每次需要分裂时，计算训练元组每个属性的增益率gain，然后选择增益率最大的属性进行分裂。

训练元组按属性进行划分信息增益gain()具体描述为

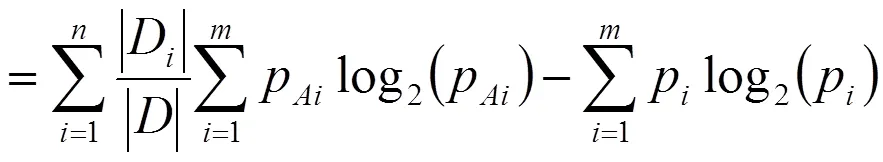
其中，为训练元组的信息量；D为第个类别分类的信息量；p为第个类别在分类元组D中出现的概率；p为第个类别在训练元组中出现的概率。

步骤4：分割成2个结点1和2。

步骤5：如果满足停止条件（剩余训练数据不可以用来进一步划分属性），决策树停止分类；否则转步骤3。

1.2　决策树的剪枝优化

在决策树构建时，决策树反映的是训练数据中的分类，而训练数据与真实情况是有一定差距的，不一定能真实反映数据的分类，可能出现过度拟合的问题。过度拟合会导致决策树分类精度不高，决策时间变长等情况。因此，本文对由训练数据生成的决策树进行剪枝，剪掉不可靠的分支之后，决策树变得更小、更简单，不仅可以提高分类精度，还可以缩短分类决策时间。本文采用后剪枝的方式对决策树进行修剪。

后剪枝的基本思想是建立测试数据集，对决策树采取统计度量的方式把最不可靠的分支剪掉，通过删除决策树的分支，用树叶代替修剪后的子树，类标号为子树中最频繁的类标记[8]。一般情况下，测试集的异常值影响决策树评估的结果，需要先对异常数据进行隔离，保留测试集有用的部分。决策树后剪枝方法的基本步骤如下：

步骤1：设训练集生成的决策树表示为，建立测试集以评估决策树的分类效果，建立评价分类效果的标准；

步骤2：用测试集中的观察集对决策树进行测试，评估决策树的性能，得出分类情况，并以此评估原决策树的错误率；

步骤3：将影响决策树质量的分支予以修剪，并用子叶代替。

1.3 决策树的染色体编码

遗传算法是一种基于生物进化的参数优化算法，基本思想是先对优化对象进行二进制编码，然后经过一系列的选择、交叉和变异操作，在满足适应度函数的条件或达到最大迭代次数后，获得近似的最优解[9]。从结构上看，决策树包含若干结点，结点与结点之间由树枝连接，可以利用决策树这种独特的结构进行二进制编码。结合遗传算法的特点，对决策树进行剪枝优化操作，以降低决策树的规模。

决策树包含若干个结点，样例决策树示意图如图1所示。所有结点按照自顶向下、先左后右的方式进行编号，编号为A，B，C，D，…，如此类推；然后对结点赋予二进制数值，数值1表示结点存在，数值0表示结点不存在；最后二进制编码按结点编号排列。图1中5号分支将被裁剪，即E结点和F结点之间的分支消失，在二进制编码中表示F结点不存在。

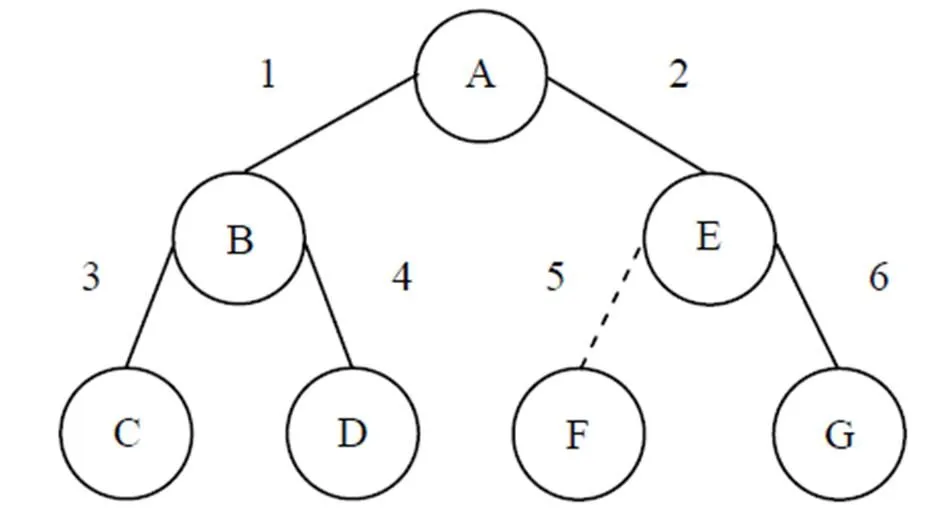
图1　样例决策树示意图

样例决策树共有6条分支，初始样例决策树的染色体二进制编码可以表示为1111111。5号分支被裁剪后，样例决策树的染色体二进制编码将变为1111101。样例决策树修剪前和修剪后的染色体数值变化如表1所示。

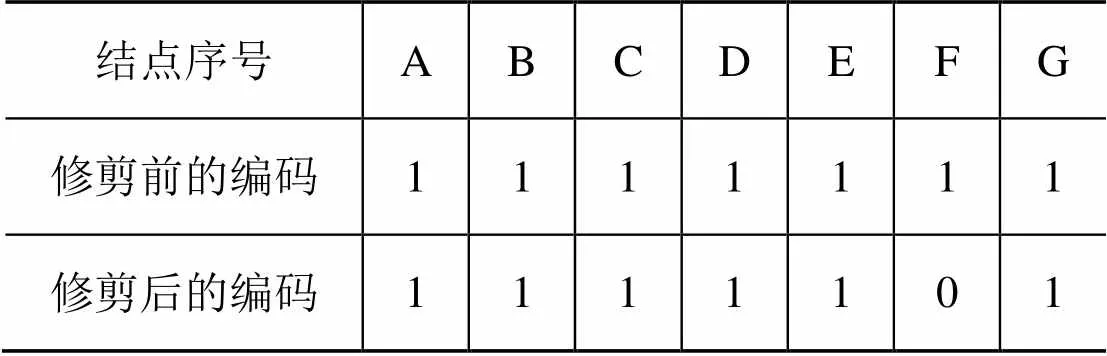
表1　样例决策树修剪前后的染色体数值变化表

1.4 适应度函数

为在优化后的决策树集合里挑选出最优决策树作为缺失数据的分类器，需要建立衡量决策树性能的标准。考虑到建立决策树的目的是对缺失数据进行属性分类，本文采用决策树的分类精度作为衡量决策树性能的指标。

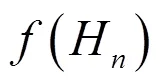
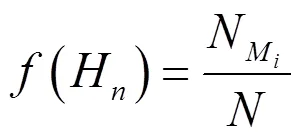
1.5　交叉运算和变异运算

为使遗传个体得到更好的优化，提高个体的适应度，可以用交叉和变异的方式进行染色体编码的改造。本文主要采用交叉和变异2种遗传运算产生后继染色体。

1）交叉运算

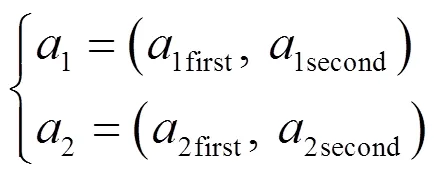
交叉运算后的染色体具体描述为

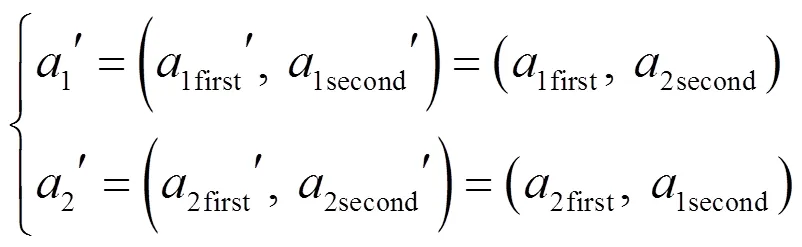
2）变异运算

变异运算是对染色体中任意的一位编码进行取反，实现染色体的变异。

1.6　自适应策略

交叉和变异操作的概率会影响遗传算法执行的过程，交叉率P和变异率P过小或过大都会影响收敛速度。遗传参数自适应策略的基本思想是：对于适应度低于平均水平的种群，加强交叉和变异操作，加快适应度低的种群完成进化速度；对于适应度高的种群，适当减少交叉和变异操作，以保留较优的种群。通过式(5)自动改变遗传算法的交叉率P，通过式(6)实现自动改变遗传算法的变异率P。

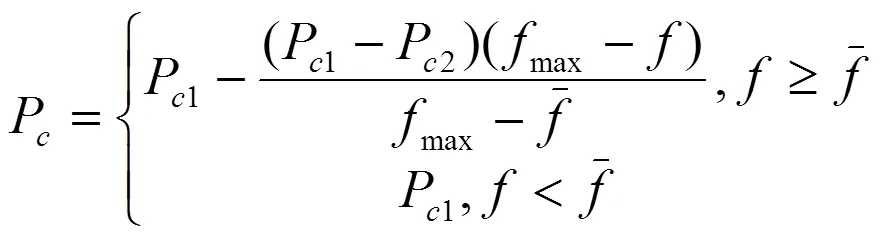
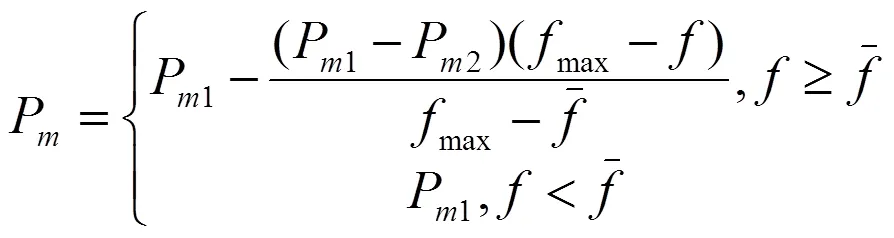
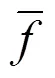
1.7　遗传算法的精英策略

种群的交叉、变异操作具有不确定性，经过交叉和变异的子代种群的优劣是未知的，如果父代种群中的优良个体也执行交叉操作，最优个体可能会被替换，因此出现了精英策略[9-11]。精英策略的基本思想是每次迭代的过程中，从父种群中挑选最优个体添加到子代种群或替换掉子代种群的最差个体，因为交叉变异的结果是未知的，而父种群中的最优个体是确定的，这样能保证子代种群的高适应度，避免进化过程中最优解变异丢失。

1.8　优化决策树的算法步骤

优化决策树的算法步骤如下：

步骤1：采集组数据，作为对决策树分类器进行剪枝操作的测试数据集；

步骤2：设定控制参数、定义适应度函数等；

步骤2-1：设定控制参数，群体规模、最大迭代次数max；

步骤2-2：变量声明，当前迭代次数、交叉概率P、变异概率P；

步骤2-3：染色体编码；

步骤2-4：计算交叉概率P、变异概率P，计算方法如式(5)和式(6)；

步骤2-5：定义适应度函数(H)，其中H为生成个决策树的编号（=1，2，…，），适应度函数计算如式(2)；

步骤3：初始化，令=0且随机生成个决策树H；

步骤4：形成种群，对每一个决策树H，计算适应度(H)；

步骤5：选择适应度最高的染色体加入新种群P；

步骤6：其余的染色体进行交叉和变异操作；

步骤7：生成种群′，计算所有新决策树的适应度(H)；

步骤8：′淘汰最小适应度的决策树，加入来自步骤5的决策树，形成新种群P；

步骤9：令种群P=P；

步骤10：当=max，转步骤11；否则转步骤4；

步骤11：适应度最高的决策树为最优的决策树。

2　EM算法

本文采用数据样本总体平均值填充缺失数据。缺失数值型数据所在集合的数据作为填充数据的参考样本。数据按照时间顺序排列，数据表示为{1，2，…，X}，是按时间排列的序号且为正整数。数据总体分为观察数据和缺失数据，观察数据是实际存在的数值，观察数据集合为obs= {1，2，…，X}，缺失数据集合为miss= {X1，X2，…，X}，是按时间排列的序号且为正整数，。

EM算法[12]步骤如下：

步骤1：变量声明，当前迭代次数（为正整数）、收敛参数（为正数）、迭代次时评价参量(k)，最大期望值(fillobs，(k))、预测值fill；

步骤3：执行最大期望步（E步），计算方法如式(7)所示；

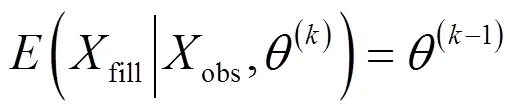
其中，(fillobs，(k))为迭代第次时填充数据期望值；(k)、(k−1)分别为迭代第次、第−1次的评价参量；

步骤4：执行最大化步（M步），计算方式如式(8)所示；

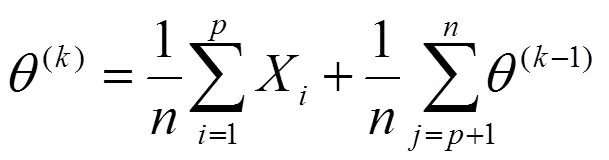
其中，(k)、(k−1)分别为迭代第次、第−1次的评价参量；X为观察数据，obs= {1，2，…，X}；

步骤5：判断是否满足收敛条件，若是转步骤6；否则=+1，转步骤3，计算方式如式(9)所示；

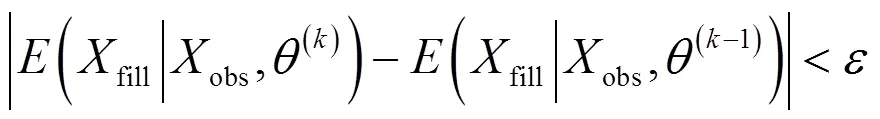
其中为收敛参数；

步骤6：输出预测值fill，并使用该值作为对本数据集所有缺失数据的填充值，计算方式如式(10)所示。

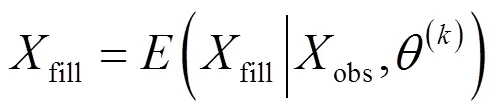
3　基于优化决策树和EM的缺失数据填充算法

基于优化决策树和EM的缺失数据填充算法步骤：

步骤1：采用最优的决策树对缺失数据进行分类，得到若干分类集合；

步骤2：EM算法初始化，以缺失数值型数据所在集合的数据作为填充数据的参考样本；

步骤3：执行EM算法，完成数据填充。

4　实验与分析

4.1　实验环境与参数设置

本次实验的CPU为Intel Core i3 3.40 GHz，内存为4 GB，操作系统为Window7 32位，开发环境为MATLAB R2013a。相关算法的参数设置如表2所示。

表2　算法的参数设置

4.2　实验结果与分析

4.2.1优化决策树的分类精度测试

为验证算法准确性，本文采用车载健康监测设备的30000条数据作为原始数据，包括心率、血压和体温等数值型数据，且所有数据都是同一人在同一环境下连续获取。原始数据生成的决策树分类精度为82.8%。在测试样本数分别为400，600，800，1000，1200时，采用相同的测试样本，分别用遗传算法和改进遗传算法对决策树进行优化操作。每个算法运行5次，选取分类精度最好的决策树进行对比。实验结果如表3、图2所示。

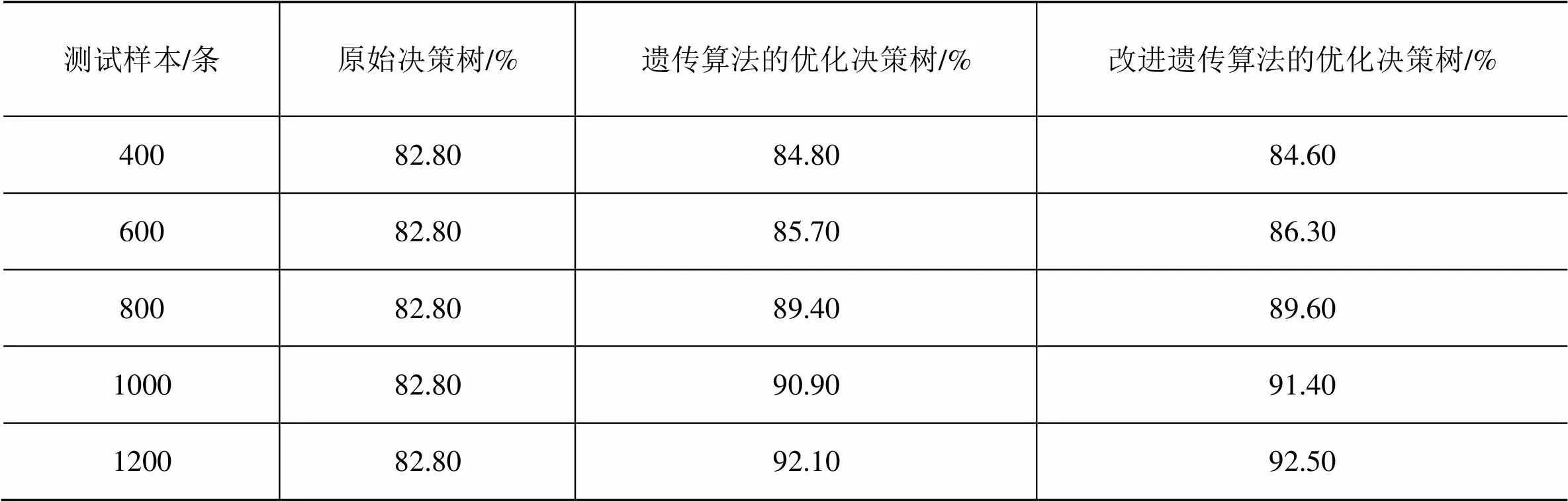
表3　原始决策树、遗传算法的优化决策树和改进遗传算法的优化决策树的分类精度测试结果

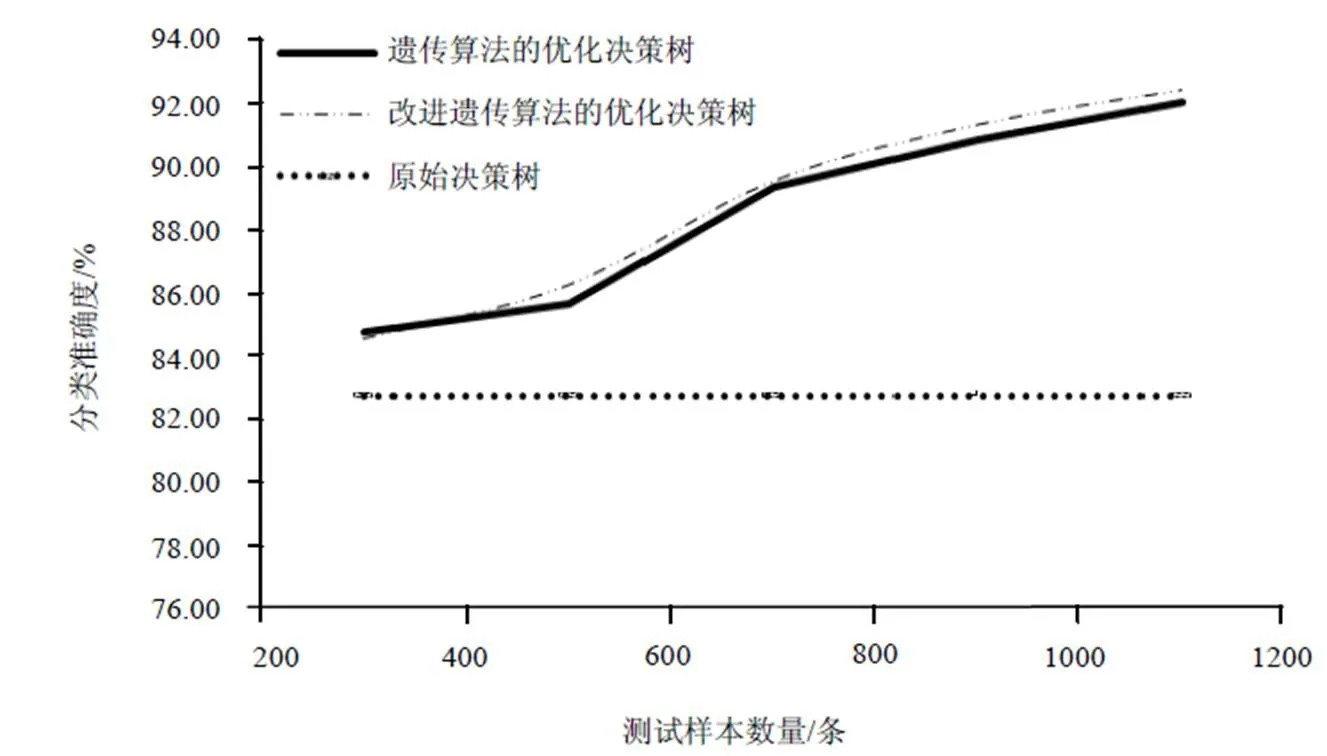
图2　2种优化决策树算法的分类精度对比图

由表3、图2可知，由于剪去了不可靠的分支，优化后的决策树分类精度明显提高。从测试样本方面看，参与决策树剪枝的测试样本越大，决策树的分类精度越高，剪枝效果越好。从分类精度方面看，改进遗传算法的优化决策树分类效果优于遗传算法的优化决策树。这是因为改进遗传算法在运行过程中对较优个体进行保留操作或者减少交叉变异操作，提高了决策树的适应度。

4.2.2填充算法的耗时对比

从原始数据集中随机抽取5组样本数据个数为3000的样本作为数据测试集。每组测试集随机删除若干个数据，生成4个不同的数据测试集，缺失数据个数分别为200，400，600，800。对每个数据集分别用基于原始决策树和EM的缺失数据填充算法、基于优化决策树和EM的缺失数据填充算法填充缺失数据。5组实验数据完成后，得出每个数据测试集的缺失数据填充时间，按缺失数据个数求出平均值。实验结果如表4、图3所示。

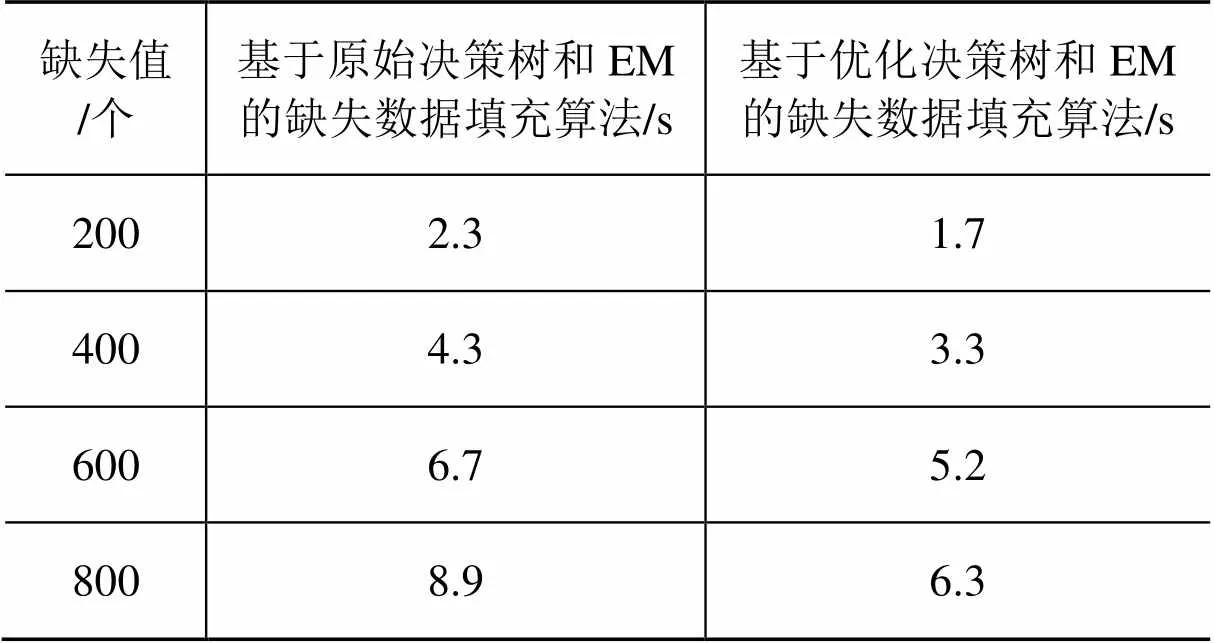
表4　基于原始决策树和EM的缺失数据填充算法、基于优 化决策树和EM的缺失数据填充算法的耗时对比

由表4、图3可知，缺失数据填充的平均耗时与缺失数据个数增加基本呈正相关的关系，缺失数据个数越多，填充数据平均耗时越长。通过对比优化前后的决策树对填充缺失数据过程平均耗时可知，优化后缺失数据填充算法的平均耗时减少了。这是因为决策树分支数减少，缩短了决策树分类器对缺失数据分类的时间。

图3　2种缺失数据填充算法平均耗时对比图

5　结论

本文提出了一种基于优化决策树和EM的缺失数据填充算法。该算法主要基于精英策略的自适应遗传算法对决策树进行优化，克服了决策树的过分拟合问题，然后结合优化后的决策树和EM算法，实现多属性数值型数据的分类和填充。本文采用车载健康监测设备采集的数据作为原始数据进行仿真，结果表明，相对于优化前的决策树算法，优化后的决策树分类精度更高，所提出算法的平均填充耗时更少。该算法具有较高的实用价值，可以有效解决多属性数值型数据缺失问题。

[1] 李宏,阿玛尼,李平,等.基于EM和贝叶斯网络的丢失数据填充算法[J].计算机工程与应用,2010,46(5):123-125.

[2] 武森,冯小东,单志广.基于不完备数据聚类的缺失数据填补方法[J].计算机学报,2012,35(8):1726-1738.

[3] 张婵.一种基于支持向量机的缺失值填补算法[J].计算机应用与软件,2013,30(5):226-228.

[4] 袁景凌,钟珞,杨光,等.绿色数据中心不完备能耗大数据填补及分类算法研究[J].计算机学报,2015,38(12):2499-2516.

[5] 李忠波,杨建华,刘文琦.基于数据填补和连续属性的朴素贝叶斯算法[J].计算机工程与应用,2016,52(1):133-140.

[6] Amiri M, Jensen R. Missing data imputation using fuzzy-rough methods[J]. Neurocomputing, 2016, 205:152-164.

[7] Turrado C C, Sánchez L F, Calvorollé J L, et al. A hybrid algorithm for missing data imputation and its application to electrical data loggers[J]. Sensors, 2016, 16(9):1467.

[8] Dong Y J, Liu T Z. Parameter optimization based on genetic algorithm in the research of equivalent pruning effect on fuzzy decision tree[J]. Advanced Materials Research, 2013, 756-759: 3809-3813.

[9] 刘全,王晓燕,傅启明,等.双精英协同进化遗传算法[J].软件学报,2012,23(4):765-775.

[10] Leno I J, Sankar S S, Ponnambalam S G. MIP model and elitist strategy hybrid GA–SA algorithm for layout design[J]. Journal of Intelligent Manufacturing, 2015:1-19.

[11] Tretyakova A, Seredynski F. A novel genetic algorithm with asexual reproduction for the maximum lifetime coverage problem in wireless sensor networks[C]. The Third International Conference on Advanced Communications and Computation, 2013: 87-93.

[12] Lin T H. A comparison of multiple imputation with EM algorithm and MCMC method for quality of life missing data[J]. Quality & Quantity, 2010, 44(2):277-287.

Missing Data Imputation Algorithm Based on Optimal Decision Tree and EM

Liang Bingyi1Cai Yanguang2Cai Hao2Qi Yuanhang2Huang Helie2Ole Hejlesen3

(1. Guangzhou No.3 Bus Company 2. School of Automation, Guangdong University of Technology 3. Department of Health Science & Technology, Aalborg University)

Focusing on the problem of missing data in large data management and application, a missing data imputation algorithm based on an optimal Decision Tree and EM is proposed to fill the tmultiple attributed missing numeric data. In order to solve excessive fitting problem of Decision Tree, the proposed algorithm adopts an optimal Decision Tree which is optimized by an adaptive genetic algorithm based on elitist strategy to classify the data, and combines with the EM to fill the numeric data. The simulation results show that: comparing with Decision Tree algorithm without optimization, the classification accuracy of the optimal Decision Tree is better and the proposed algorithm need less time to fill data.

Data Imputation; Decision Tree; Expectation Maximization Algorithm; Genetic Algorithm

梁秉毅，男，1991年生，硕士，研究方向：计算机技术与应用。E-mail: byleuang@foxmail.com

蔡延光，男，1963年生，博士，教授，博导，主要研究方向：网络控制与优化、组合优化、智能优化、智能交通系统等。

国家自然科学基金（61074147）；广东省自然科学基金（S2011010005059）；广东省教育部产学研结合项目（2012B091000171，2011B090400460）；广东省科技计划项目（2012B050600028，2014B010118004，2016A050502060）；广州市花都区科技计划项目（HD14ZD001）；广州市科技计划项目（201605121347368）。