一种快速预测卫星过顶的简易模型

于文浩,张云,杨树瑚,洪中华,韩彦岭

(上海海洋大学 信息学院,上海 201306)

一种快速预测卫星过顶的简易模型

于文浩,张云,杨树瑚,洪中华,韩彦岭

(上海海洋大学 信息学院,上海 201306)

准确预报卫星的过顶信息在军用、民用等多个领域内有重要的应用,文中通过卫星轨道参数来计算卫星星下点轨迹,结合观测到的卫星方位角和仰角等信息反推卫星ECEF坐标,通过局部星下点轨迹吻合与校准建立一种简易模型,使用MATLAB程序进行预测未来某时间段卫星过顶时间,画出卫星星下点轨迹,并计算出卫星过顶的仰角、方位角。本文提出的模型简易有效,无需专业卫星预测软件,仅仅只需MATLAB软件就可以预测指定卫星的过顶情况。

过顶预测;星下点轨迹;坐标转换;仰角;方位角

0 引 言

我国的空间环境不仅是商业观测卫星感兴趣的地方,更是全球军事侦察卫星最为关注的区域,每年有数十颗高分辨率对地观测卫星反复从我国上空经过[1],随着目前遥感卫星相关技术的飞速发展,观测站接收和处理数据的技术也有了迅猛的发展。

卫星过顶时间是指卫星经过通信终端头顶, 能够进行通讯的一段时间。对于遥感卫星的数据接收和处理需通过建立遥感地面观测站等相关平台来完成,这就要求地面观测站天线能够精确地对准遥感卫星[2]。

卫星相对于地面观测站的空间位置是随着时间不断变化的,观测站观测卫星方位角及其仰角需要涉及轨道求解[3]、坐标转换以及大地测量学等相关知识。目前有学者基于STK软件进行卫星实时运动的仿真设计[4],基于改进的时间搜索算法[2]以及采用对卫星轨道进行递推算法[3]进行卫星的过顶时间预测。

现在市场上已经开发出了许多的卫星仿真或预测软件,比如STK(Satellite Tool Kit),只要输入时间、地点和卫星参数,就可以比较精确地预报卫星的过顶情况。本文不使用任何卫星轨迹预测软件,基于卫星轨道参数计算卫星星下点轨迹[5-6]并结合坐标转换算法,构建一种简易预测模型,反推卫星过顶时间及其仰角与方位角。

1 卫星过顶预测模型的构建

1.1由卫星仰角及方位角反推其ECEF坐标

站心坐标系通常以用户所在的位置点P为坐标原点,三个坐标轴分别是相互垂直的东向、北向和天向(或者称为天顶向),因而站心坐标系又称东北天(E、N、U)坐标系[7]。如图1所示,站心坐标系的天向与大地坐标系在此点的高度方向一致。站心坐标系固定在地球上,是地球坐标系的一种[8]。假设观测站P点在大地坐标系中的坐标为(φ,λ,h)；φ为观测站P点的纬度；λ为观察站P点的经度；h为从P点到基准椭球面的法线距离。

可以在站心坐标系中计算卫星在观测站处的观测矢量。如图2所示,θ为天线仰角;a为天线方位角度; 用PS表示观测矢量。

将观测站的大地坐标(φ,λ,h)转换为ECEF坐标(x,y,z),并假设在ECEF坐标系中卫星位置点S的坐标为(x(s),y(s),z(s)),则从观测站到该卫星的观测矢量为

图1 站心坐标系与大地坐标系

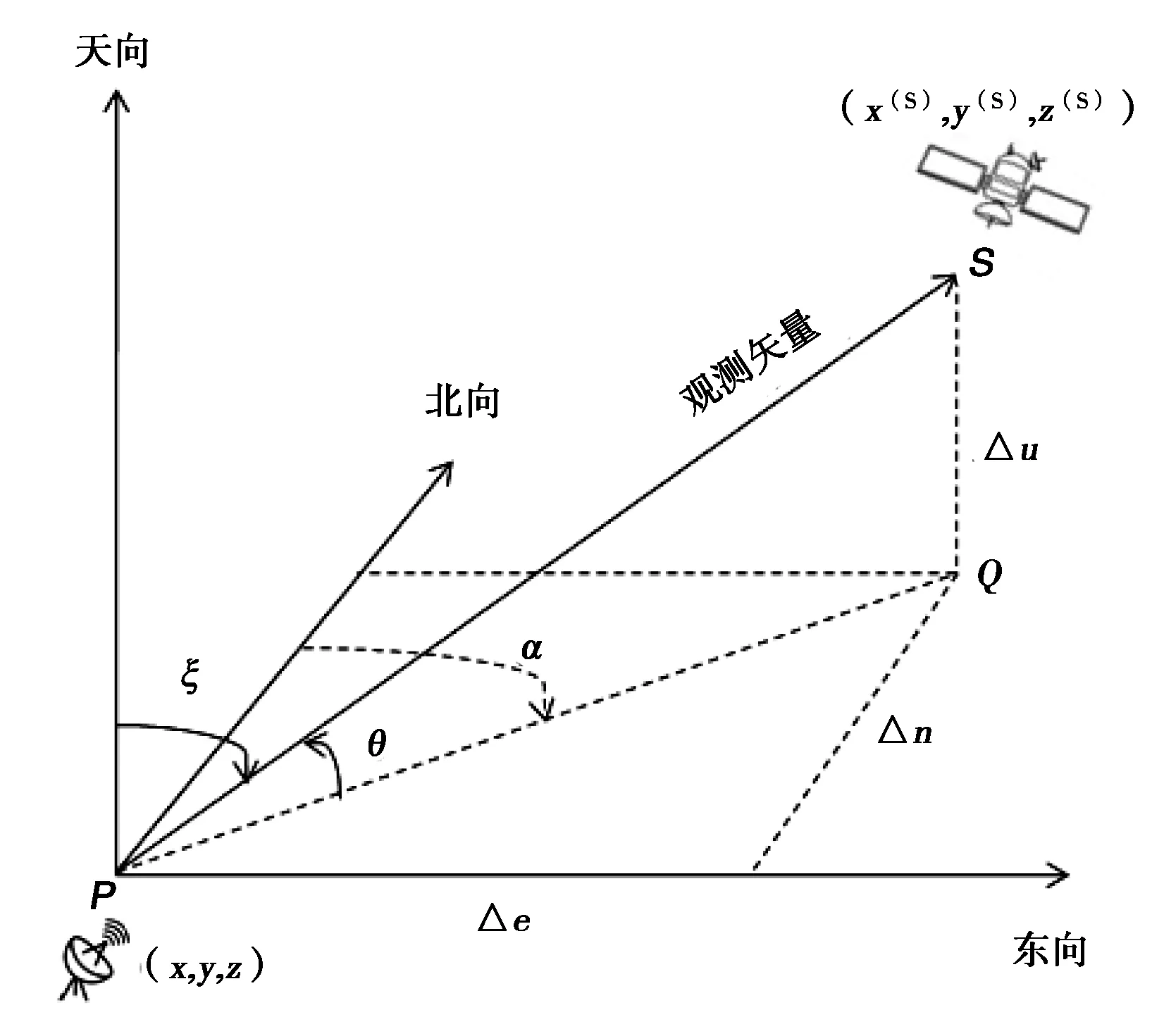
图2 站心坐标系仰角与方位角

(1)

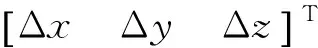
(2)

反过来,观测矢量的站心坐标也可变换到ECEF坐标系中,相应的变换公式为

(3)

其中,坐标变换矩阵S为

(4)

式中：λ,φ如图1所示。

根据图2仰角与方位角的几何关系,用PS表示观测矢量,得到

Δe=|PS|× cos(θ)×sin(a),

Δn=|PS|×cos(θ)×cos(a),

Δu=|PS|×sin(θ)

分别把式(4)和式(3)带入式(1),得到卫星位置点S的ECEF坐标为

(5)

1.2卫星星下点计算

卫星与地球中心连线在地球表面的交点称为星下点[9]。卫星运动和地球自转使星下点在地面移动所画出的轨迹称为星下点轨迹。不同的卫星运行轨道会产生不同的星下点轨迹;并且由于地球不停地自转,同一卫星后一圈的星下点轨迹一般不再重复前一圈的星下点轨迹。近圆轨道是卫星经常采用的一种轨道方式,当其满足一定精度要求时,可将其看作圆轨道进行处理[10-11]。

假设卫星在地心惯性坐标系中的坐标为R-SATE,

R-SATE=S-RAAN×S-I×S-W×

R-SAT,

(6)

(7)

其中:R-SAT为卫星在轨道坐标系中的坐标;S-RAAN为卫星升交点赤经的变换矩阵;RA为卫星升交点赤经

(8)

式中:S-I为轨道倾角变换矩阵;i为轨道倾角。

(9)

式中:S-W为卫星近地点幅角变换矩阵;W为卫星近地点幅角。

综合式(6)～式(9)计算卫星星下点经纬度,

Longitude=arctan(R-SATE-Y/R-SATE-X),

Latitude= arctan(R-SATE-Z/sqrt

(R-SATE-X＾2+R-SATE-Y＾2)),

(10)

式中，R-SATE-X,R-SATE-Y和R-SATE-Z分别为R-SATE在地心惯性坐标系的分量。

1.3数据处理流程

结合上面建立的数学模型,预测卫星未来某个时间段被观测到的过顶情况。模型分两个支路来进行,最后结合两个支路建模。

图3 卫星过顶预测数据处理流程

首先第一个支路根据通过观测站观测到的卫星仰角、方位角,通过上述站心坐标系模型来计算卫星的ECEF坐标,再将卫星的ECEF坐标转换为星下点的大地坐标。

第二个支路根据卫星轨道参数,建立卫星星下点轨迹模型,计算任意时刻的卫星星下点。

将两个支路进行结合,即由卫星参数得出星下点轨迹与根据卫星仰角、方位角数据计算出的局部星下点坐标进行轨道配准,其目的是使实验观测周期等于1时的星下点轨迹与所假设的第一个过顶时间对应的卫星星下点轨迹相吻合。然后依据卫星每日绕行的周数来确定后一天与前一天的时间间隔,得到卫星在未来时间段内的星下点。

由于卫星星下点轨迹覆盖全球,对于指定的观测区域仅需要少量的星下点轨迹即可获取指定区域观测站可观测到的所有卫星的运行轨迹。

在本文的模型中,有效区域是从已知星下点的经纬度中选出最大跨度的区域,并且在有效区域内筛选出星下点的大地坐标,再将星下点的经纬高坐标转换为卫星的ECEF坐标,推算出卫星与观测站之间的仰角和方位角。由于在卫星定位中,当天线仰角小于10°的时候,卫星信号很弱不能有效的进行定位,因此从中筛选出仰角≥10°作为卫星的过顶情况。具体建模过程如图3所示。

2 仿真数据

本次实验采用模拟仿真的卫星过顶数据,仿真数据中包含卫星的部分轨道参数;连续三天(Day0～Day2)的模拟观测站观测到的卫星过顶数据,数据包含观测时间内的卫星最高和最低仰角,以及对应时刻的方位角,以及观测站距离卫星的粗略距离，如表1所示。本文以近圆轨道的星下点轨迹为例进行仿真。

表1 模拟观测站观测的连续三天卫星过顶数据

部分卫星参数:倾斜角:97.418°;升交点赤经:318.063°;偏心率:0.000 2;近地点幅角:36.122°;每日绕行圈数:15.259 5;周期:94.37 min;半长轴:6 866 km;

模拟某观察站(北纬:32.020 9°;东经: 118.768 1°)

本文将通过仿真数据结合图3的算法预测卫星在Day3以及Day5的过顶情况。

3 仿真过程及结果分析

图4中黑色箭头所指的方块(下图同)为MATLAB给出的模拟观测站的位置信息(北纬32.020 9°,东经: 118.768 1°)

图4 模拟观测站的位置

依据图3预测卫星运行规律所建立模型的原理,首先根据Day0～Day2所给出的卫星的仰角、方位角,并结合1.1小节的计算公式反推出卫星的ECEF坐标,然后再计算出其星下点。图5～图7给出Day0～Day2卫星过顶时间的星下点轨迹,图中标记出卫星过顶的时候,观测站第一次观测到的时刻,并且图7中Day2的开始时间为12:25的过境的轨迹上,最高仰角处已经几乎到达观测站的正上方(箭头所示),与所给的模拟数据观测仰角为82.8°较吻合。

图5 卫星Day0天过顶情况及星下点轨迹

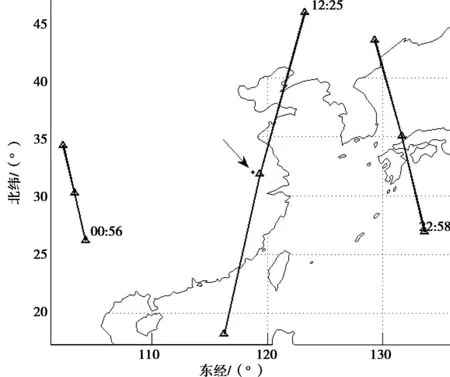
图7 卫星Day2天过顶情况及星下点轨迹

经计算Day0～Day2卫星的星下点的经纬度最大区间为E(102°,134°),N(18°,47°),设为观测区间S.假设未来几天的卫星星下点落入区间S并且卫星仰角≥10°,即为观测站观测到的卫星过顶情况,并计算其对应的过顶时间,根据卫星的轨道参数计算其星下点轨迹。

根据预测模型将实验的周期数设为4天(Day0～Day3),然后根据时间节点画出Day3所有星下点轨迹,并且截取观测区间S内的局部星下点,如图8所示。将观测区间S内的局部星下点以及其对应的时间间隔进行提取,将其转化为卫星的ECEF坐标,求解其对应的仰角方位角,最后截取仰角≥10°的星下点即为卫星过顶信息,如图9粗体轨迹所示(在图8的基础上)箭头指向为卫星的运行方向,箭头尾部的时间为卫星过顶的起始时间。卫星的预测过顶起止时间、星下点坐标、仰角、方位角如表2所示。

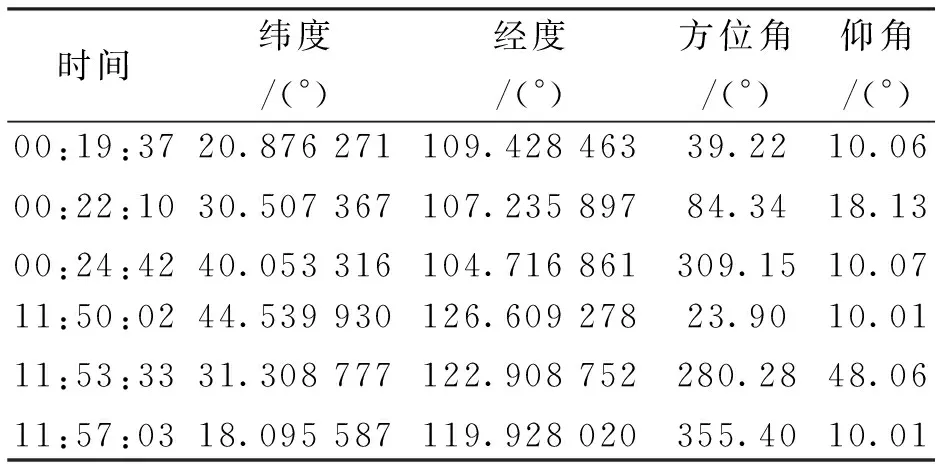
表2 Day3天观测区间S内卫星过顶情况

图8 卫星Day3天在观测区间S的星下点轨迹

图9 卫星Day3天在观测区间S内仰角≥10的星下点轨迹

如图8所示,观测站观测到Day3卫星在观测区域S内一共有4条过境轨迹,进行10°的仰角截取之后,如图9所示, 第一次观测的有效的过顶时间为凌晨00:19:37-00:24:42,地面的经纬度跨度为N(20.876 271°～ 40.053 316°),E(104.716 861°～109.428 463°),卫星运行方向自南向北、自东向西,最高仰角为18.13°.第二次观测的有效的过顶时间为上午11:50:02-11:57:03,地面的经纬度跨度为N(18.095 587°～ 44.539 930°),E(119.928 020°～ 126.609 278°),卫星运行方向为自北向南、自东向西,最高仰角为48.06°,第二次观测的最高仰角属于较高仰角,并且过顶时段处于中午时分,对该地区的侦察威胁较大。

根据预测模型将实验的周期数设为6天(Day0～Day5),然后根据时间节点画出Day5天所有星下点轨迹,并且截取观测区间S内的局部星下点,如图10所示。卫星过顶信息如图11粗体轨迹所示(在图10的基础上)箭头指向为卫星的运行方向,箭头尾部的时间为卫星过顶的起始时间。卫星的预测过顶起止时间、星下点坐标、仰角、方位角如表3所示。

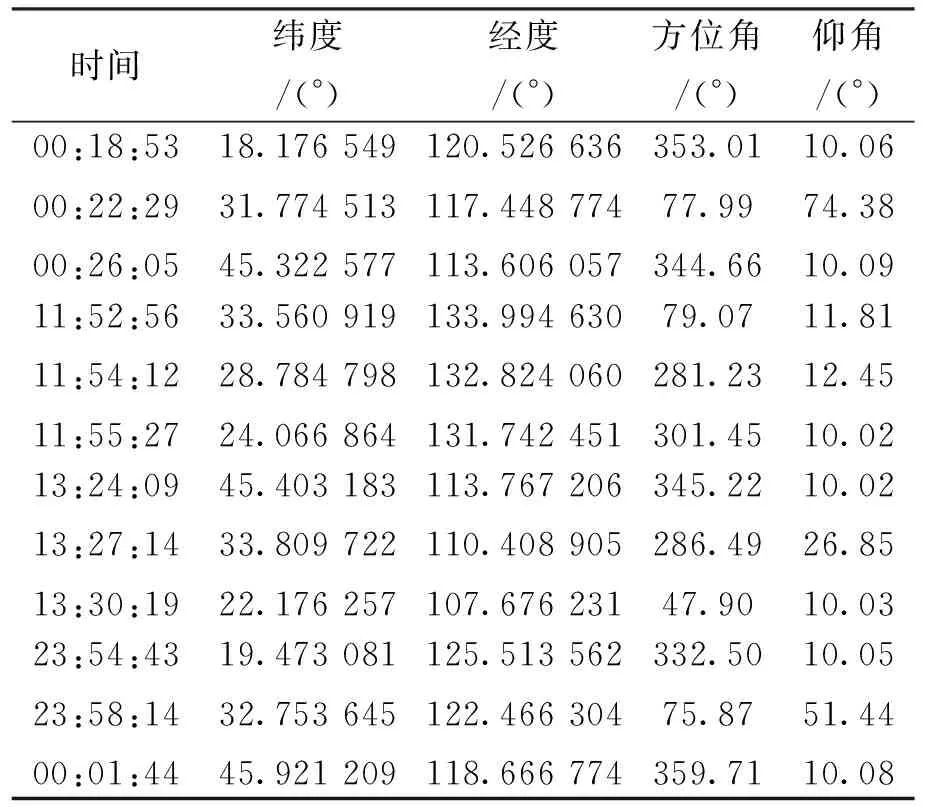
表3 Day5天观测区间S内卫星过顶情况

图10 卫星Day5天在观测区间S的星下点轨迹

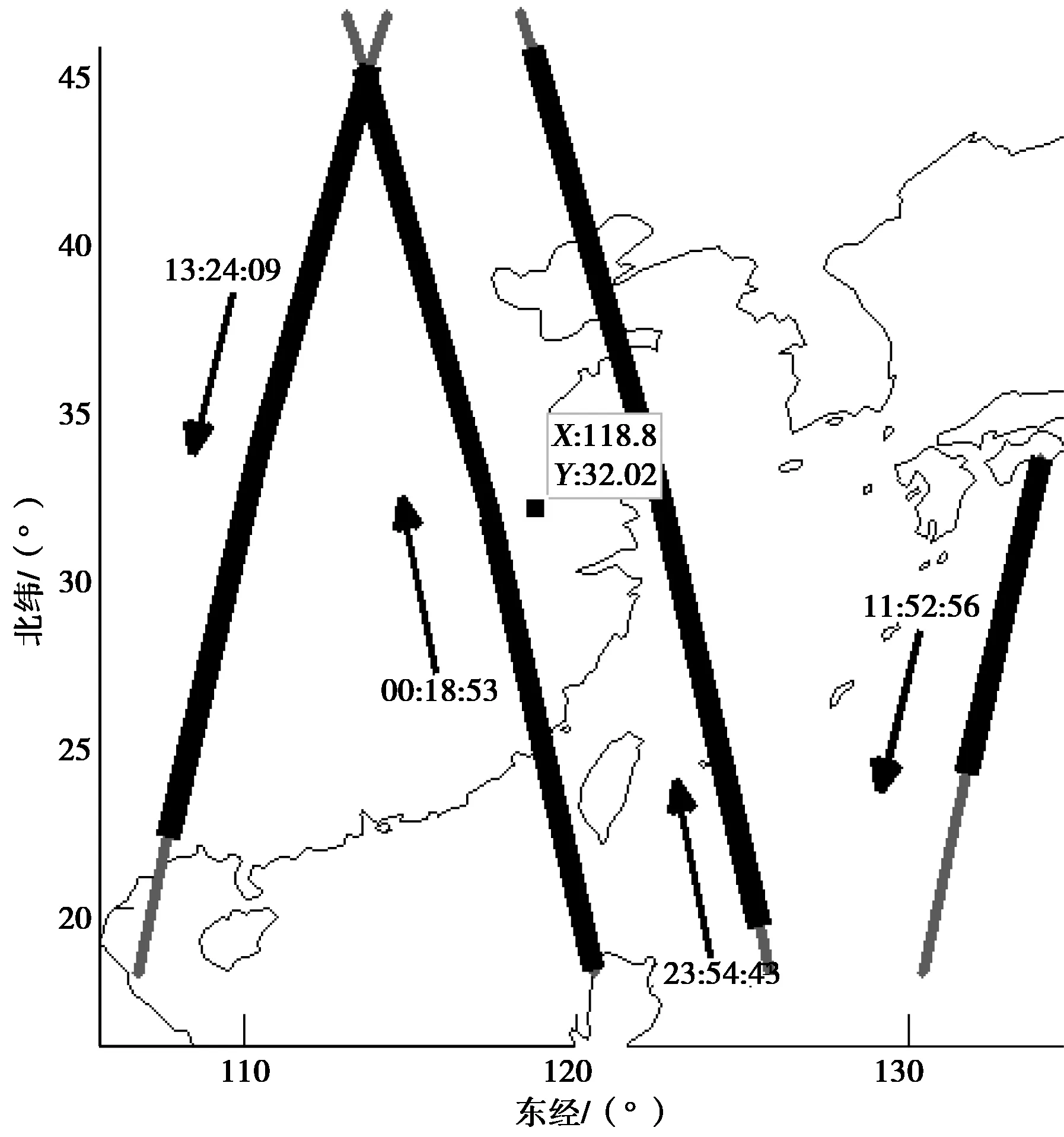
图11 卫星Day5天在观测区间S内仰角≥10的星下点轨迹

如图10所示,观测站观测到Day5卫星在观测区域S内一共有4条过境轨迹,进行10°的仰角截取之后,如图11所示 第一次观测的有效的过顶时间为凌晨00:18:53-00:26:05,地面的经纬度跨度为N(18.176 549°～ 45.322 577°),E(113.606 057°～120.526 636°),卫星运行方向为自南向北、自东向西,最高仰角为74.38°.该仰角属于高仰角,虽然时间处于凌晨时分,但是如果是雷达成像照相侦察卫星,它能够全天候、全天时进行侦察,并有一定的穿透能力,对侦察地区威胁比较大。第二次观测的有效的过顶时间为上午11:52:56-11:55:27,地面的经纬度跨度为N(24.066 864°～ 33.560 919°),E(131.742 451°～ 133.994 630°),卫星运行方向为自北向南、自东向西,最高仰角为12.45°.第三次观测的有效的过顶时间为下午13:24:09-11:30:19,地面的经纬度跨度为N(22.176 257°～45.403 183°),E(107.676 231°～ 113.767 206°),卫星运行方向为自北向南、自东向西,最高仰角为26.85°.第四次观测的有效的过顶时间为晚上23:54:43-次日凌晨00:01:44,地面的经纬度跨度为N(19.473 081°～45.921 209°),E(118.666 774°～125.513 562°),卫星运行方向为自南向北、自东向西,最高仰角为51.44°,属于较高仰角,对侦察地区会构成一定威胁。

4 结束语

掌握卫星的过顶情况,可以准确地计算出侦察卫星将经过地面目标的时刻,并能充分利用卫星过顶的间隙和“空白”进行一系列重要活动。

相对于通过设置参数直接使用STK卫星工具包计算卫星轨道信息以及过顶预测来讲,文中所提出的算法模型方便、快捷、实用。虽然算法本身具有一定的近似性,但是它已能够较好地满足遥感卫星规划阶段的要求并且不依赖于相关的预测软件,在轨道设计 、覆盖评估等方面有其实际应用价值,有利于工程应用的推广。

[1] 吴浩. 商业卫星?侦察卫星![J]. 国防,2013(7):78-80.

[2] 王鹏,刘海涛,杨根庆. 一种小卫星过顶预报算法[J]. 上海航天,2002(5):17-19,38.

[3] 罗伊萍,解志刚,陈文锋. 一种有效的卫星过顶预报方法[J]. 海洋测绘,2006(3):13-16.

[4] 杜耀珂. 基于STK的卫星实时视景仿真系统设计[J]. 空间控制技术与应用,2009(2):60-64.

[5] 卫国宁,骆剑,康志宇,等. 一种星下点精确重访约束下的轨道设计方法[J]. 中国空间科学技术,2016(4):67-73.

[6] ABDELKHALIK O. Initial orbit design from ground track points[J]. Journal of Spacecraft and Rockets, 2015, 47(1): 202-205.

[7] 凌震莹. 大地坐标系与站心地平直角坐标系的坐标转换[J]. 声学与电子工程, 2009(4):31-34.

[8] 刘光明,唐颖哲. 大地位置坐标系探讨[J]. 测绘科学与工程, 2008(4):31-33.

[9] 张大洪. 星下点轨迹[J]. 数理天地(高中版), 2010(4):46-47.

[10] 段方,刘建业. 一类由星下点反算卫星近圆回归轨道的方法[J]. 中国空间科学技术, 2006,(3):38-43.

[11] 张云彬,张永生. 近圆轨道遥感卫星星下点轨迹的计算[J]. 测绘科学技术学报, 2001(4):257-259.

AForecastModelofCoveringTimeForSatellites

YUWenhao,ZHANGYun,YANGShuhu,HONGZhonghua,HANYanling

(CollegeofInformationTechnology,ShanghaiOceanUniversity,Shanghai201306,China)

Accurate prediction of satellite's covering information is an important application in the military and civil field, it calculates the sub-satellite point track using the orbit parameters and deduces ECEF coordinate of satellite by means of combination of elevation and azimuth, establishing a simple model through the calibration of partial sub-satellite point track, using MATLAB programming to predict the future period of satellite covering time and draw the sub-satellite point track and calculate the elevation/azimuth of satellite's covering period. The model is simple and effective, using the Matlab only instead of professional satellite prediction software.

Covering prediction； sub-satellite point track； coordinate transformation； elevation angle； azimuth angle

10.13442/j.gnss.1008-9268.2017.04.013

P228.4

A

1008-9268(2017)04-0070-07

2017-05-12

联系人: 于文浩E-mail: 786015778@qq.com

于文浩(1991-),男,硕士研究生,主要从事GNSS定位导航技术研究。

张云(1974-),男,博士,教授,主要从事GNSS定位导航,GNSS-R技术研究。

杨树瑚(1983-),男,博士,讲师,主要从事电磁波,极地冰盖物理过程的技术研究。