GNSS多通道级联群时延特性对零值叠加的影响

刘寄奴,刘文祥,王飞雪

(国防科技大学 电子科学与工程学院 卫星导航定位技术工程研究中心,湖南 长沙 410073)

GNSS多通道级联群时延特性对零值叠加的影响

刘寄奴,刘文祥,王飞雪

(国防科技大学 电子科学与工程学院 卫星导航定位技术工程研究中心,湖南 长沙 410073)

导航信号从卫星发射到用户接收处理,中间可能存在多级通道,通道的群时延特性会对时延估计零值产生影响。目前较为普遍的做法是将各通道零值进行简单叠加得到级联通道的零值,针对级联通道的零值结果是否简单等于各通道零值之和还尚未有研究。本文定量分析了级联通道群时延特性对时延估计零值的影响,研究了级联通道时延估计零值的叠加特性,并在软件接收机上对分析结果进行了仿真验证。结果表明,零阶群时延通道与其他通道级联时,零值满足叠加特性;奇数阶群时延通道的零值为零,所以奇数阶群时延通道间级联时零值满足叠加特性;其他群时延通道相互级联时,零值不满足叠加特性,若对群时延系数进行约束,可使零值近似满足叠加特性。

通道级联;群时延;零值;叠加特性

0 引 言

时延估计是直接序列扩频测距系统接收的一个重要估计量,它一般通过跟踪电路获得伪码相位信息,进而与参考时间信息差分得到时延估计[1]。卫星信号从卫星发射到最终的用户接收处理,这个过程中存在着多级的通道,各通道均会对级联通道的时延估计产生影响。

有大量的文献研究了通道非理想对时延估计的影响。朱峰[2]选取椭圆滤波器作为模拟的中频滤波器,仿真分析了不同相关器间隔下信号经过滤波器前后的时延相对变化情况。余宜珂[3]研究了几种中频带通滤波器群时延特性对时延估计的影响,比较了测距码码率不同的情况下,群时延特性对时延估计的影响。耿虎军[4]从系统带内群时延变化的规律和幅度两个方面,分析了其对时延估计随机误差和系统误差的影响;许晓勇[1]建立了时延估计的分析模型,导出了通道等效低通滤波器h(t)为任意实函数时,群时延响应和幅频响应与时延估计的对应关系。目前针对级联通道的时延估计零值是否等于各子通道时延估计零值叠加之和,

尚未有研究。

针对上述情况,本文理论上分析了通道群时延特性对时延估计零值的影响。研究了级联通道时延估计零值的叠加特性,并在软件接收机上对结果进行了仿真,仿真结果与理论分析一致。

1 群时延特性对时延估计零值的影响

1.1级联通道群时延特性

群时延定义为相位对角频率的微商,对系统的相频特性用泰勒级数展开,可以得到级数形式的群时延表达式[5-9]

τ(ω)= -dφ(ω)/dω=-a1-2a2(ω-ωc)-

3a3(ω-ωc)2+…,

(1)

式中,ωc为中心频点,可以看出,通道的群时延特性表现为一系列不同类型的群时延相叠加的形式,零阶项表示的时延量为常数值,与信号频率之间没有关系,也是理想通道群时延特性的表现形式,一阶项被称之为一阶群时延特性,二阶项被称之为二阶群时延特性,三阶以上的高阶项对信道群时延的影响很小,可以忽略[10]。

1.2时延估计模型

导航信号从卫星发射到接收机接收,各环节引入的通道特性,可以用其低通等效形式级联等效成一个总的低通滤波器hL(t)。其过程可以等效简化为图1中的时延估计简化模型,其中,s(t)是伪码信号。

图1 时延估计简化模型

ε).

(2)

当滤波器特性非理想时,波形将产生失真,这时ε与滤波器特性的关系不再直观。需要根据具体的时延估计参数来确定零值与滤波特性之间的关系[1]。

1.3群时延特性对零值的影响

1.2节中的时延估计器通常选用非相干早迟码估计器,对于伪码信号,非相干早迟码估计器实现结构如图 2所示,其中d为早迟码间隔。

图2 非相干早迟码估计器实现结构

由文献[1]可知当估计器稳定时,低通滤波器的通道特性A(f)ejφ(f)和时延估计零值ε的关系可以表示为

(3)

式中:Tc为码片宽度;b为信号接收带宽;sinc2(fTc)为当信号为BPSK信号时,相关函数所对应的功率谱密度,当信号为其他类型时,分析过程类似。由于通道幅频特性对零值的影响可以忽略[11],且本文主要考虑群时延特性对零值的影响,因此假定A(f)=1,可得:

(4)

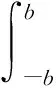
ε=F′[φ(f)].

(5)

2 时延估计零值的叠加特性

图 3是级联通道时延估计零值的叠加特性的示意图,若ε1=F′[φa(f)]、ε2=F′[φa(f)],ε=F′[φa(f)+φb(f)],则ε=ε1+ε2时,表示级联通道的时延估计零值满足叠加特性。

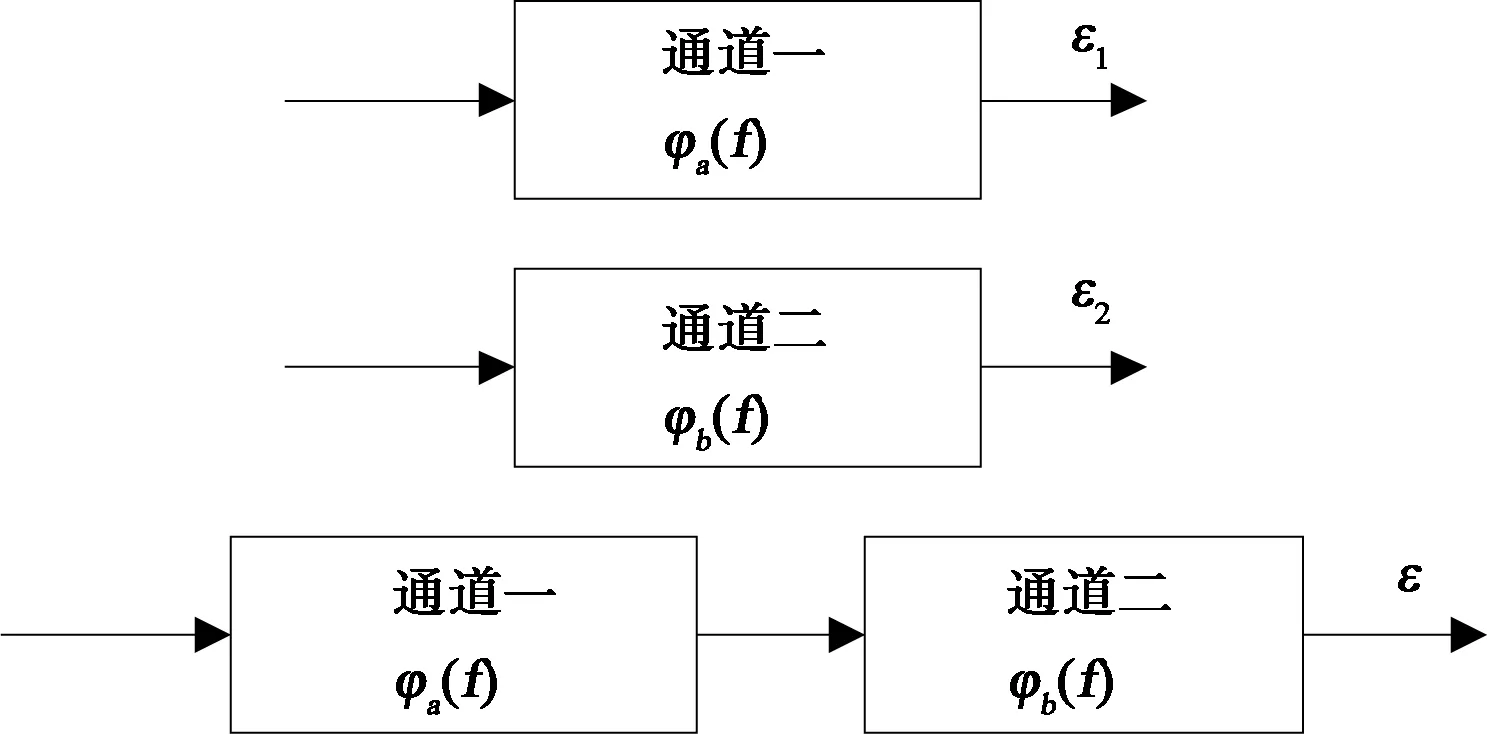
图3 叠加特性示意图

同时,定义|ε1+ε2-ε|为时延估计零值差,并假设|ε1+ε2-ε|<0.5 ns时,时延估计零值近似满足叠加特性。

由于接收信号经过的信道模型均可以等效到基带的通带特性,因此为使后续分析简便,可以假设中心频点fc=0,此时,参照1.1节,分别定义零阶群时延通道、一阶群时延通道、二阶群时延通道、二次多项式群时延通道的相频特性为

φ0(f)=-2πfτ0,

(6)

(7)

(8)

(9)

其中:τ0为零阶群时延系数;α为一阶群时延系数;β为二阶群时延系数。

零阶群时延通道与任意通道φ′(f)级联时,由式(4)易得ε=τ0+F′[φ′(f)],因此级联通道的时延估计零值满足叠加特性。

一阶群时延通道间级联时,由式(4)易得ε=F′[φ1(f)]=0,也即一阶群时延引入的时延估计零值为零,因此级联通道的时延估计零值满足叠加特性。

2.1二阶群时延通道间级联

二阶群时延通道与二阶群时延通道级联时,级联通道相频特性可以表示为

(10)

从理论公式推导并不能直接得到结论。由式(4),画出时延估计零值随二阶群时延系数β变化的曲线图。易知,只有当变化曲线为过零点直线时,时延估计零值才满足叠加特性。

图 4 (a)示出了相关间隔为0.1Tc,接收带宽为信号主瓣带宽,不同码率下,时延估计零值ε随二阶群时延系数β变化曲线,图中虚线为曲线的过零点切线。图4 (b)为码率为5.115 MHz时的变化曲线。由图可知,曲线呈非线性,因此二阶群时延通道间级联时,时延估计零值并不满足叠加特性。

图4 时延零估计零值随二阶群时延系数变化曲线 (a)不同码率下;(b)码率为5.115 MHz

在二阶群时延系数较小时,曲线近似过零点直线。若以“切线与曲线之差不超过0.5 ns”作为“近似直线”的约束,可对二阶群时延系数进行约束。以码率为5.115 MHz时的情况为例,在群时延系数在零到临界值9.7 ns/MHz2范围内,变化曲线可以近似成直线,因此,若β1、β2大于零,则当β1+β2<9.7 ns/MHz2时,有0<ε1+ε2-ε<0.5 (ns),也即级联通道的时延估计零值近似满足叠加特性。考虑β1、β2可能出现小于零的情况,由式(4),可得出类似的结论,具体为“当|β1|<9.7 ns/MHz2, |β2|<9.7 ns/MHz2,且 |β1+β2|<9.7 ns/MHz2时,有|ε1+ε|<0.5 (ns)。”

对应码率1.023 MHz、2.046 MHz、5.115 MHz、10.23 MHz,“近似直线”的临界值分别为720 ns/MHz2,114 ns/MHz2,9.8 ns/MHz2,1.5 ns/MHz2,可以看出,码率越大,临界值越小。

由上述分析知,在主瓣接收且码率不超过10.23 MHz的情况下,若约束二阶群时延系数|β1|<1.5 ns/MHz2, |β2|<1.5 ns/MHz2, |β1+β2|<1.5 ns/MHz2,则二阶群时延级联通道的时延估计零值近似满足叠加特性。

2.2一阶群时延通道与二阶群时延通道级联

一阶群时延通道与二阶群时延通道级联时,级联通道相频特性可以表示为

(11)

图 5(a)是相关间隔为0.1Tc,接收带宽为信号主瓣带宽,一阶群时延系数α=10 ns/MHz,不同码率下,时延估计零值差ε1+ε2-ε随二阶群时延系数β变化的曲线图。由图可知,码率为1.023 MHz、2.046 MHz时,时延估计零值差近似等于零,可以认为此时级联通道时延估计零值近似满足叠加特性。且码率越大,时延估计零值差越大。

因此,研究码率为10.23 MHz下时延估计零值的近似叠加特性。

图 5(b)是相关间隔为0.1Tc,接收带宽为信号主瓣带宽,码率为10.23 MHz,一阶群时延系数α为不同的数值时,时延估计零值差ε1+ε2-ε随二阶群时延系数β变化的曲线图。由图可知,一阶群时延系数越大,时延估计零值差越大,且随着二阶群时延系数增大,时延估计零值差逐渐收敛到零。

图5 时延估计零值差随二阶群时延系数变化曲线 (a)不同码率下；(b)码率为10.23 MHz

图 6是在图5 (b)条件下,时延估计零值差最大值max[ε1+ε2-ε]随一阶群时延系数α变化的曲线图。从图可知,码率为10.23 MHz时,约束max[ε1+ε2-ε]<0.5 ns,可以进一步约束一阶群时延系数小于临界值2.8 ns/MHz,上述讨论默认α值大于零,对于存在α可能小于零的情况,根据式(4),有类似结论,具体为“当|α|<2.8 ns/MHz时,有|ε1+ε|<0.5(ns)”.

图6 时延估计零值差最大值随一阶群时延系数变化曲线

由上述分析知,在主瓣接收且码率不超过10.23 MHz的情况下,若约束|α|<2.8 ns/MHz,一阶群时延和二阶群时延级联通道的时延估计零值近似满足叠加特性。

2.3二次多项式群时延通道间级联

由1.1节知,大部分群时延通道可以近似表示为二次多项式群时延,因此,两个群时延通道的相频特性可以表示为

(12)

(13)

级联通道的相频特性可以表示为

(14)

此时,通道的级联可以分解成零阶群时延通道与其他通道级联、一阶群时延通道间级联、二阶群时延通道间级联、一阶群时延通道与二阶群时延通道级联的情况。则由2.1、2.2小节中的分析知,此时级联通道的零值同样不满足叠加特性,若约束|α1|<2.8 ns/MHz,|α2|<2.8 ns/MHz,|α1+α2|<2.8 ns/MHz,|β1|< 1.5 ns/MHz2,|β2|< 1.5 ns/MHz2,|β1+β2|< 1.5 ns/MHz2,则在主瓣接收且码率不超过10.23 MHz的情况下,有

-0.5<εβ1-ε1<0.5、-0.5<εβ2-ε2<0.5、

-0.5<εβ-ε<0.5、-0.5<εβ1+εβ2-εβ<0.5,

(15)

3 仿真验证

图7是通道群时延特性为二阶群时延时,理论值和仿真值的对比图。其中,理论值是给定群时延特性和时延估计参数之后,求解式(4)得到的。软件仿真值通过下述方法得到:针对某系统某频点BPSK(10)信号的接收,首先生成理想信号,接着将其在频域与群时延通道的表达式相乘,由IFFT变换,得到通过群时延通道的信号。然后,由软件接收机对信号进行接收带宽滤波,跟踪稳定后,统计码相位均值,得时延估计零值。软件接收机的参数设置如下:码环噪声带宽BL=2 Hz,相干积分时间Tcoh=1 ms,码率为10.23 MHz,相关间隔取d=0.1Tc,接收带宽取信号主瓣带宽20.46 MHz.图7中,仿真值和理论值最大差值不超过0.17 ns,充分证明了1.3小节中公式的正确性。

表1示出了信号经过不同群时延通道后时延估计零值的软件接收机仿真结果。其中,通道群时延特性由零阶、一阶、二阶群时延系数τ0、α、β表征。ε1表示信号经过通道一后,时延估计零值的仿真值。ε2表示信号经过通道二后,时延估计零值的仿真值。ε表示信号经过上述两通道的级联通道后,时延估计零值的仿真值。

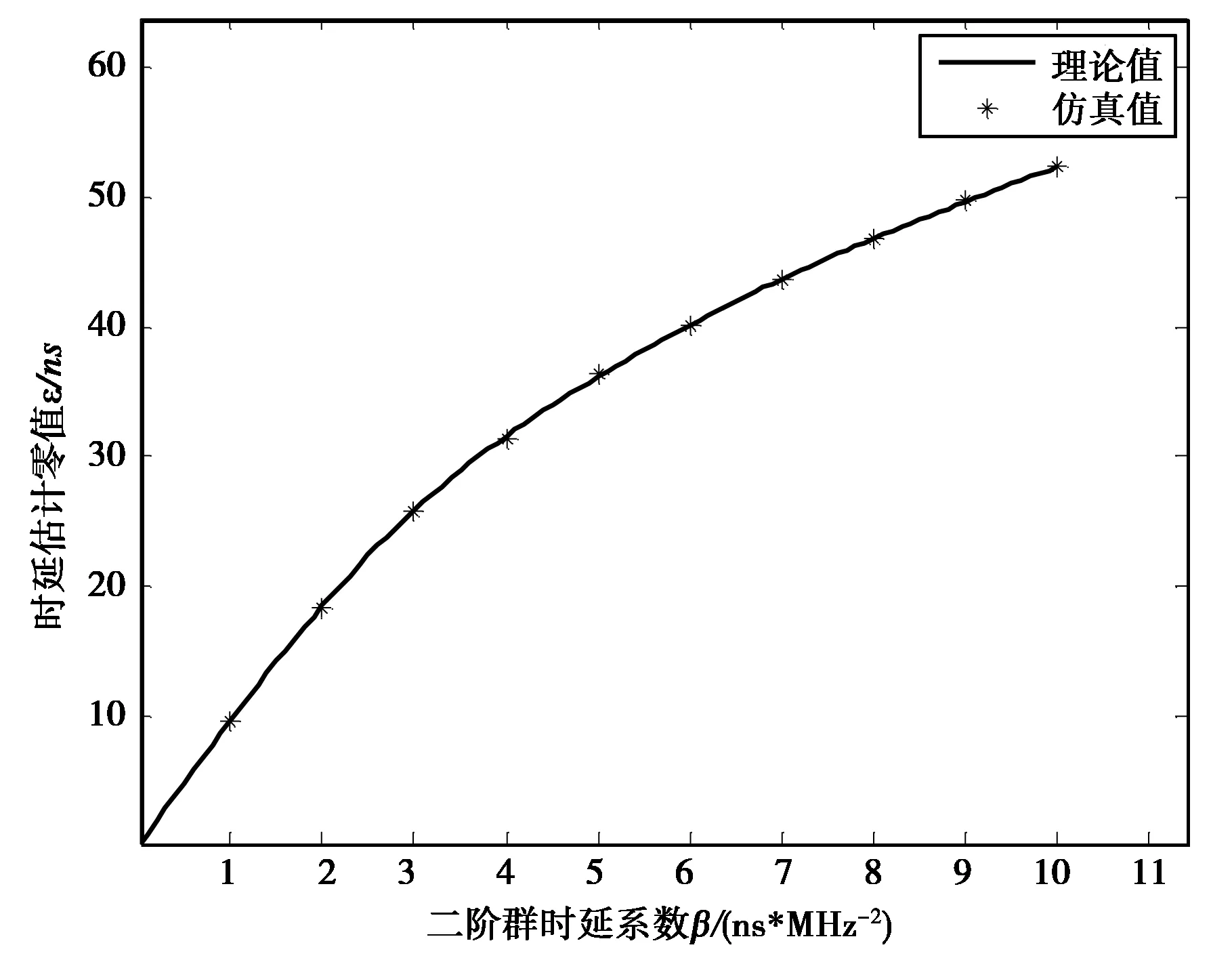
图7 理论值仿真值对比图

通道群时延特性(τ0:ns、α:ns/MHz、β:ns/MHz2)仿真结果/ns零值差/ns群时延类型通道一φa(f)通道二φb(f)ε1ε2ε|(ε1+ε2)-ε|φa(f):零阶φb(f):二次多项式τ0=10α=1,β=1,τ0=19.9610.5720.620.09φa(f):一阶φb(f):一阶α=5α=10-0.01-0.020.040.07φa(f):二阶φb(f):二阶β=0.5β=0.54.904.909.630.17β=0.5β=14.909.6314.250.28β=0.5β=1.54.9014.2518.460.69β=0.5β=24.9018.4622.331.03φa(f):一阶φb(f):二阶α=1β=5036.3336.260.07α=2β=5036.3336.130.20α=3β=5036.3335.890.44α=4β=50.0136.3335.590.75α=5β=5-0.0136.3335.191.13φa(f):二次多项式φb(f):二次多项式α=0.5,β=0.5,τ0=5α=1,β=1,τ0=59.8314.6424.100.37α=1,β=1,τ0=5α=1.5,β=1.5,τ0=514.6419.1031.981.76α=1.5,β=1.5,τ0=5α=2,β=2,τ0=519.1023.1938.094.2α=2,β=2,τ0=5α=2.5,β=2.5,τ0=523.1927.0042.907.29α=2.5,β=2.5,τ0=5α=3,β=3,τ0=527.0030.2347.0910.14α=3,β=3,τ0=5α=3.5,β=3.5,τ0=530.2333.2250.4912.96

零阶级联二次多项式以及一阶级联一阶时,时延估计零值差小于0.1 ns,考虑到软件接收机本身存在一定的误差,可以认为此时零值满足叠加特性。二阶级联二阶、一阶级联二阶与二次多项式级联二次多项式时,时延估计零值差随群时延系数的增大而增大,约束群时延系数在一定范围内时,时延估计零值差小于0.5 ns,可以认为此时零值近似满足叠加特性。对于一阶级联二阶时,α=3>2.8 ns,而|(ε1+ε2)-ε|=0.44 ns<0.5 ns的情况,考虑到第3节中的理论临界值是最为苛刻的条件,因此理论临界值小于实际临界值属于正常现象。因此,表中的结果可以说明第3节中结论的正确性。

4 结束语

本文从理论上阐述了通道群时延特性对时延估计零值的影响,分析了不同群时延通道级联时,级联通道时延估计零值的叠加特性,并用软件接收机进行了仿真验证。结果表明,零阶群时延通道与其他通道级联时,零值满足叠加特性。奇数阶群时延通道的零值为零,奇数阶群时延通道间级联时零值满足叠加特性。其他群时延通道相互级联时,零值不满足叠加特性,若对群时延系数进行约束,可使零值近似满足叠加特性。论文分析结果可用于通道设计、通道非线性补偿、观测数据预处理等。

[1] 许晓勇. 卫星导航接收机高精度建模、分析及优化设计研究[D]. 长沙:国防科学技术大学,2008.

[2] 朱 峰,李孝辉,王国永. 滤波器群时延分析及其对导航信号的影响[J]. 电子测量技术,2013,36(5):54-57.

[3] 余宜珂,王萌,郭伟,等. GNSS接收机中频带通滤波器群时延对伪距测量影响的研究[J]. 电子测量技术,2014,37(3):24-28.

[4] 耿虎军.系统群时延特性对伪码测距影响的研究[J]. 无线电工程,2004,34(11): 27-29.

[5] 肖志斌.高精度导航接收机的群时延建模、测量和校准技术[D].长沙:国防科技大学,2014.

[6] 朱祥维.卫星导航系统时间同步关键技术研究[D].长沙:国防科技大学,2007.

[7] BOYD R W,GAUTHIER D J,GAETA A L.Maximum time delay achievable on propagation through a slow-light medium[J].Physical Review A,2005(71):023801-1-4.

[8] BASHKANSKY M,BEADIE G,DUTTON Z,etal.Slow-light dynamics of large bandwidth pulses in warm rubidium vapor[J].Physical Review.A ,2005(72):033819.

[9] STENNER M D, Neifeld M A,ZHU Z M,etal. Distortion management in slow-light pulse delay[J].Optics Express ,2005,13(25):9995-10002.

[10] 李蓬蓬.导航卫星信道模拟器关键技术研究[D].长沙:国防科技大学，2014.

[11] 李彩华,张鑫，庞晶，等. BOC导航接收机伪码测距零值分析[J].宇航学报,2011，32(11)：2351-2356.

TheInfluenceofGroupDelayunderGNSSMultichannelCascadeonSuperpositionofZeroValue

LIUJinu,LIUWenxiang,WANGFeixue

(SatelliteNavigationandPositionR&DCenter,SchoolofElectronicScienceandEngineering,NationalUniversityofDefenseTechnology,Changsha410073,China)

There may be several channels for the navigation signal to propagate from the satellite to the user, of which the group delay characteristics influence the zero value of time delay estimation. It is common practice to simply add the zero value of each channel to obtain zero value of cascaded channel, whether the sum of the zero values of each channel is simply equal to the zero value of the cascade channel has not been studied yet. In this paper, the influence of the group delay characteristics on the zero value is analyzed quantitatively. And the superposition characteristic of the zero value of time delay estimation under the cascade channel is estimated. The result of the simulation is verified on the software receiver. The results show that when the zero-order group delay channel and other channels are cascaded, the zero value satisfies the superposition characteristic. Since the zero value of the first-order group delay channel is equal to zero, it satisfies the superposition characteristic too. For other situations, the zero value does not satisfy the superposition characteristic, while the zero value can be approximately to satisfy it when the group delay coefficient is constrained.

Cascaded channel; group delay; zero value; superposition characteristic

10.13442/j.gnss.1008-9268.2017.04.003

P228.4

A

1008-9268(2017)04-0015-07

2017-07-15

国家自然科学基金(批准号:41604016)

联系人: 刘寄奴 E-mail: liu_nu@163.com

刘寄奴(1994-),男,硕士研究生,研究方向为星基导航与定位技术。

刘文祥(1981-),男,博士,副研究员,研究方向为星基导航与定位技术。

王飞雪(1971-),男,博士,教授,博士生导师,主要研究方向为卫星导航定位/扩频信号处理、电子系统抗干扰。