基于GNSS的晶振驯服方法分析

薛毅聪,龚航,刘增军,朱祥维

(国防科技大学 电子科学与工程学院 卫星导航定位技术工程研究中心,湖南 长沙 410073)

基于GNSS的晶振驯服方法分析

薛毅聪,龚航,刘增军,朱祥维

(国防科技大学 电子科学与工程学院 卫星导航定位技术工程研究中心,湖南 长沙 410073)

高稳定度、高准确度的频标在计量测试、测控通信、电信电力、金融等领域至关重要。GNSS驯服晶振结合了GNSS具有较高长期稳定度和晶振具有较高短期稳定度的优点,加之成本较低,获得了广泛应用。本文针对GNSS驯服晶振的特点,对比分析了最小二乘法、无偏滑动平均滤波法、Kalman滤波法等几种主要的晶振驯服滤波方法,并利用相同控制方法进行驯服仿真比对,给出了几种滤波方法的驯服性能差异,分析了其优缺点。本文可以为驯服晶振在GNSS授时接收机的应用提供技术借鉴。

GNSS;晶振驯服;最小二乘;Kalman滤波

0 引 言

在导航定位、计量测试、测控通信、电信电力、金融等领域中,许多设备都需高精度的时间频率基准进行协调同步工作,并且随着导航、测量技术的发展,要求频率标准精度越来越高[1]。在一般情况下,可以利用高稳定的恒温晶体振荡器来实现,准确度可达到10-9量级,在要求精度更高的场合可以选用铷钟作为频率标准,其准确度可达10-11量级[2]。但是采用晶体振荡器或者铷钟作为频率标准的时统设备都存在一个问题:长期频率漂移造成频率准确度降低。然而更高一级的频率标准(氢钟,铯钟)成本高,设备体积大,不能满足普遍使用需求。所以提供一个高精度、低成本、满足普遍使用需求的频率标准源非常关键。

GNSS具有高精度的频率基准(达到10-12～10-15),用户可以通过GNSS授时接收机提取卫星系统的同步时钟频率,但是GNSS信号受大气传输、相对论效应等因素影响[3],接收机在接收解调的过程中会引入各种噪声,导致恢复出来的时钟频率虽然能够跟踪卫星信号的长期稳定度,但是也增加了短期的相位抖动,短期稳定度指标差。然而晶体振荡器如OCXO、VCXO等具有短期稳定度好的优点,但存在老化的固有缺陷,长期稳定度差。在此基础上发展出来的基于GNSS的晶振驯服技术能有效的结合上述的两种优点,实现高稳定度的频率输出。

本文分析了基于GNSS的晶振驯服技术基本工作原理,针对GNSS驯服晶振的误差模型特点,对比分析了最小二乘法、无偏滑动平均滤波法、卡尔曼滤波法等目前几种主要的滤波方法,并利用常用的控制算法,进行晶振驯服仿真验证,从而给出了几种方法的优缺点以及适用条件。

1 基于GNSS的晶振驯服技术原理

对于GNSS晶振驯服技术的基本工作原理如图1所示,利用GNSS授时接收机解算的钟差,进行滤波处理计算出频率偏移量后,利用相应的控制算法计算出加到晶振上的压控电压所对应的数字量,并通过高分辨率的D/A转换器输出该控制电压,达到校正晶体振荡器输出频率的目的[4],使晶振的振荡频率锁定在GNSS时钟上,从而提高晶振的长期稳定性。最终目的是实现GNSS卫星授时长期稳定性高和本地晶振短期稳定度高的优势互补。

图 1 基于GNSS的晶振驯服基本原理框图

由上述原理可知,GNSS驯服晶振的主要环节是钟差滤波算法和频率控制方法,以下分别展开讨论。

2 几种常用滤波方法分析

在GNSS晶振驯服系统中,误差来源受各项因素的影响,一方面系统精度与GNSS授时接收机输出的钟差有密切联系,然而GNSS授时接收机解算的钟差由于受卫星星历误差、电离层、对流层等因素影响存在误差;另一方面根据晶振自身的误差模型特点,晶振的频率偏差、老化和温度变化引起的频率漂移率等也会造成影响。

根据晶振误差模型,将其按照泰勒级数展开,并考虑晶振自身的特点,取泰勒级数的前三项,就满足基于GNSS晶振驯服的要求[5].模型表达式为

xn=x0+x1τn+τ2n2x2/2+v(n),

(1)

式中:n的取值为1,2,3,…;τ为时间间隔;x0为初始频率误差;x1为晶振初始频率偏差;x2为老化和温度变化引起的线性频率漂移率。

υ(n)是由GNSS接收机钟差解算引起的误差,包含多种误差成分,如: 1) 卫星时钟误差; 2) 星历误差; 3)电离层的附加延时误差; 4) 对流层的附加延时误差; 5)多路径误差; 6)接收机本身的误差等。而上述的误差可以采用相应的模型或者其他钟差修正方法进行修正处理,本文主要考虑修正后残留误差引起的噪声。目前主要的钟差滤波方法有最小二乘法、无偏滑动平均滤波法、卡尔曼滤波法等,以下分别进行分析讨论。

2.1最小二乘法

最小二乘法是通过最小化误差的平方寻找数据的最佳函数匹配。基于GNSS的晶振驯服误差模型式(1),记录n秒脉冲时钟,计数器测得的值分别为Y1,Y2,Y3…Yn,这些测量值与初始频率误差x0、晶振初始频率偏差x1、老化和温度变化引起的线性频率漂移率x2的联系可由下式表示[6]:

(2)

根据上述矩阵求解可得晶振引入的初始频率、晶振初始频率偏差、老化和温度变化引起的线性频率漂移率这三个误差参数。在存在随机噪声的情况下,最小二乘法利用求得的数据与实际数据之间误差的平方和为最小的准则拟合计算使得给定测量的数据点的基本趋势无限“逼近”真实值,拟合时间越长,求得的误差值越接近真实值。

2.2无偏滑动平均滤波法

文献[5]提出了一种无偏滑动平均滤波方法,是在普通滑动滤波[7]基础上进行的改进,根据基于GNSS的晶振驯服误差模型式(1),为了滤除GNSS接收机钟差解算残留修正误差υ(n),首先采用普通滑动滤波方法对钟差进行滤波,考虑到晶振误差模型频差存在,滤波时采用了滑动加权的方法,滤波表达式为

(3)

式中:N为滑动窗口窗长;Wi(n)为滤波器的第i个测量值的权值系数。由于晶振误差模型中存在一、二次项,采用普通滑动滤波得到tn时刻的xn估计值存在偏差。为了补偿估计偏差,在滤波之后采用线性最小二乘法估计xn,其表达式为

(4)

最小二乘估计采用的是方差最小准则,可用x(tn)代替tn时刻频差真实值xn计算普通滑动滤波的偏差。整理代入计算得到Wi(N)的表达式:

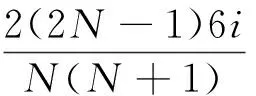
(5)

由上式可知Wi(n)是i的单调递减函数,i=0时,得到最大值2(2N-1)/(N2+N),i=N取得最小值-2(N+1)/(N2+N),说明离xn越近的测量误差值对估计xn贡献越大,这与实际情况相符[5]。

由上述可知，无偏滑动平均滤波法实际是利用线性回归对普通算术滑动平均滤波器进行了改进,滤除了GNSS接收机钟差解算残留修正误差υ(n)、晶振的频偏、频率漂移。改进后的平均滑动滤波器权值表达式简单,窗长N确定可以根据系统的需求确定,当窗口值较大时,信号平滑度较高,灵敏度较低;当窗口值较小时, 信号平滑度较低,但灵敏度较高。

2.3卡尔曼滤波法

卡尔曼滤波是一种基于最小均方误差准则的最优线性时域滤波器,是一种高效率的自回归滤波器,能够在包含噪声的信号中估计动态系统的状态。假设在n时刻解算得到的钟差为X(n),则系统状态方程为

X(n)=AX(n-1)+BU(n)+W(n),

(6)

观测方程为

Z(n)=HX(n)+V(n),

(7)

其中:n为时间系数;A和B为系统状态转移矩阵,反映了系统从n-1时刻的状态到n时刻状态的变换关系;U为系统的已知输入;W为过程噪声向量;H为线性连接矩阵;V为观测噪声[2]。

在基于GNSS的晶振驯服系统中,钟差上报的时间间隔为1s,X(n)为N时间差的真值,因此X(n)是一组三维向量,主要包括钟差、频差、频漂的数据;Zn为包含观测误差的测量值,也是一组三维向量。由于系统对于GNSS接收机钟差信号没有控制量,因而可得U(n)为0.在实际的接收信号的过程中,信号是平稳一致的,因而系统参数A为1,观测矩阵H(n)为1,对于观测噪声R的取值,依据经验必须为1,否则钟差值会在滤波后整体地变大或变小。对于过程噪声方差矩阵Q为三阶方阵,其对角线上的元素对应状态向量中各项的过程噪声方差,而其余项分别是状态向量中各项之间的协方差,各项具体数据由试验确定。简化后的滤波器运算复杂度大大降低,迭代公式为

X(n)=X(n-1)+W(n),

Z(n)=X(n)+V(n),

P(n|n-1)=P(n-1|n-1)+Q,

X(n|n)=X(n|n-1)+

Kg(n)[Z(n)-X(n|n-1)],

P(n|n-1)=[1-Kg(n)]P(n|n-1).

(8)

基于GNSS的晶振驯服基本原理与卡尔曼滤波的“预测-实测-修正”反复递推迭代的算法相符合,适合在晶振驯服系统中运用。在晶振驯服过程中,卡尔曼滤波能有效解决最佳线性滤波和估计的问题,对GNSS授时接收机钟差解算残留误差有明显的效果,经过多次测量和反复控制后,最终使得晶振输出同步于GNSS授时接收机,从而实现对晶振的驯服和调整。与此同时采用该算法在晶振守时方面有比较明显的优势,即在GNSS接收机由于其他外部原因中断钟差数据时,该系统能根据观测数据来预测下一次的测量值,使得晶振驯服系统具有较好的守时能力。

3 驯服控制方法

目前常用的控制算法有很多,比如PID控制、Fuzzy模糊控制、Optimal优化控制、Robust控制算法等等,在GNSS的晶振驯服系统中,控制量比较简单,并且系统为闭环的反馈调节系统,采用典型的PID闭环控制方法较为合适。PID控制方法是一种线性控制系统,图2示出了一个对输入误差e(n)进行控制的基本的PID控制系统结构。

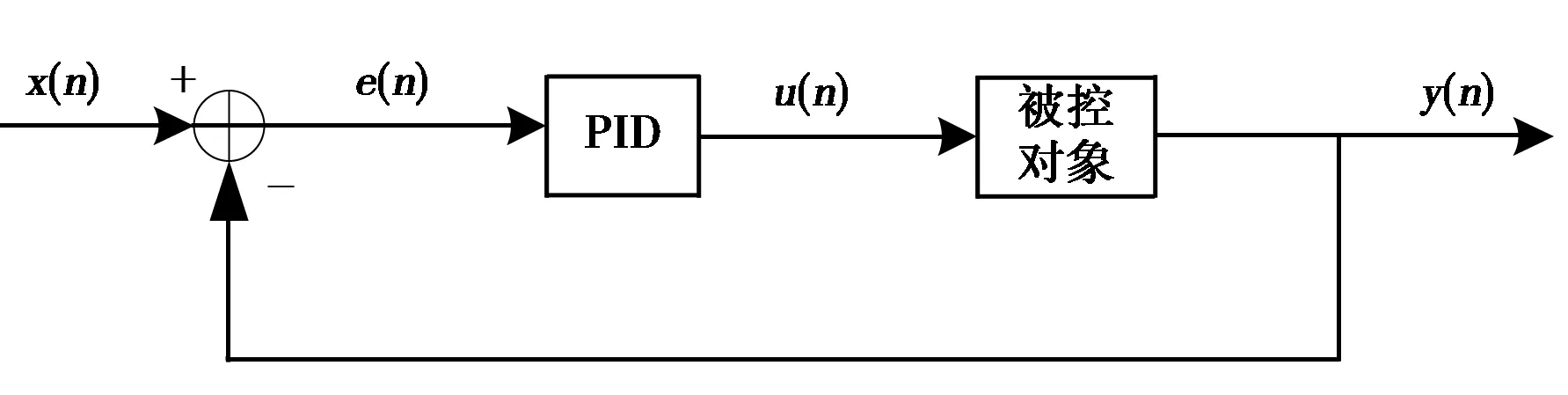
图2 PID控制基本结构

图中：x(n)为系统输入；y(n)为当前输出； 输入与输出的偏差为e(n)。在控制方法方面统一采用比例调节器进行仿真,控制简单、快速,其输出和输入的误差成比例关系,它用于调节偏差值,并在调节后将偏差控制在一定的固定值上,比例调节器的表达式为

u=KCe+u0，

(9)

式中:KC为比例系数;u0为控制量的基准,即e=0时的控制量。其中KC越大,控制作用越强,调节幅度也越大,KC越小控制作用越弱,调节幅度也越小[8]。

4 仿真实验与方法比较

根据晶振的误差模型分别对上述三种方法进行仿真。仿真条件为:初始频率误差x0=0,晶振初始频率偏差x1=1×10-5,老化线性频率漂移率x2=1×10-10,GNSS授时接收机钟差解算残留修正误差υ(n)用均值为零、标准差为40 ns的白噪声,采样间隔为1 s,其中无偏滑动平均滤波的窗口N取值为100.驯服实验结果如图3、图4所示。

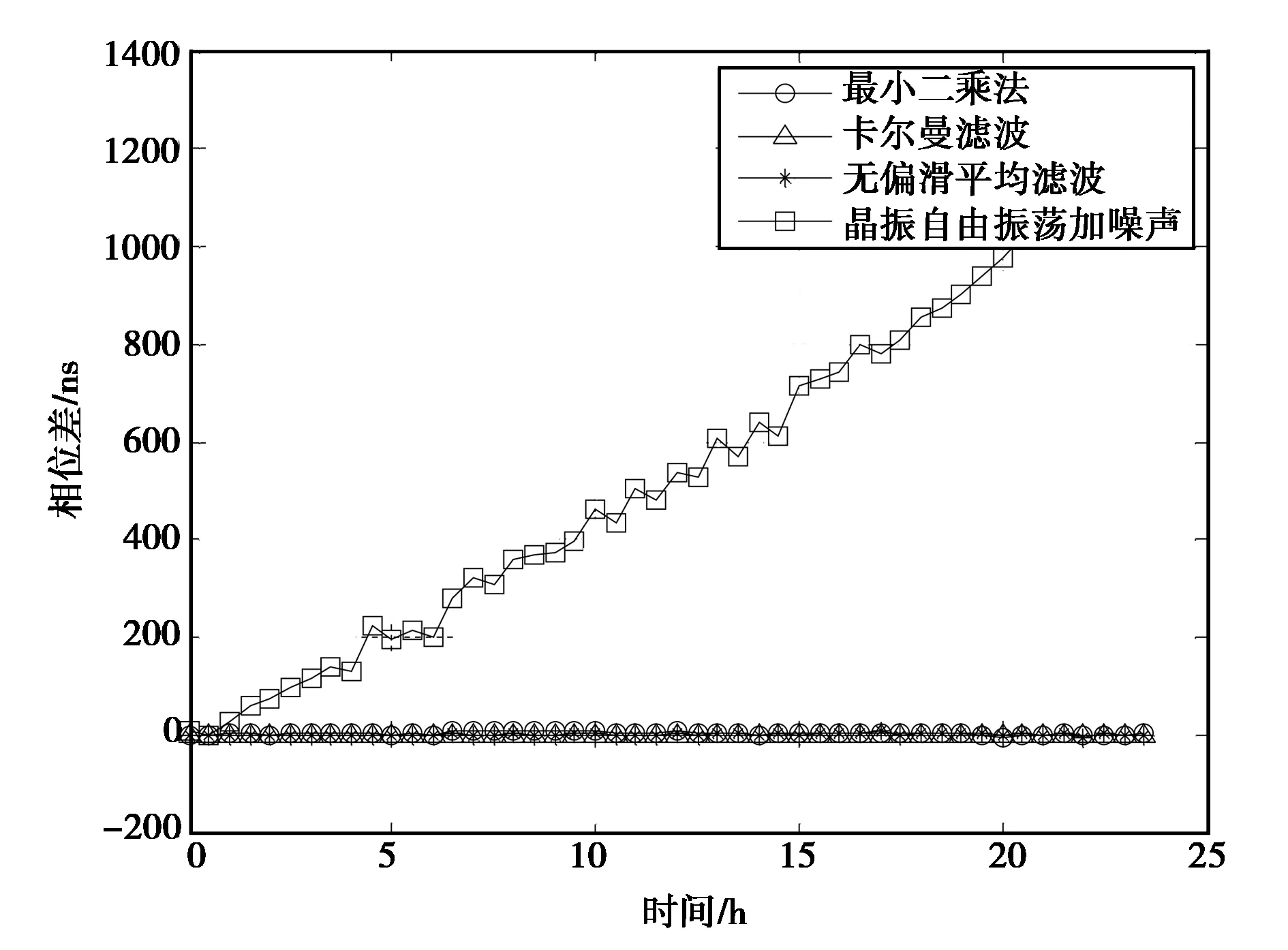
图3 晶振驯服结果比较

图4 三种方法驯服结果比较

三种方法对晶振输出的短期稳定度、长期稳定度[2,5-6]、24 h相位漂移等指标进行了对比,结果如表1所示。

表 1 三种方法的指标比较

根据上述方法比较及实验结果,可以得出以下结论:

1) 三种方法均能实现晶振的驯服,驯服后系统的短期稳定度指标相对于晶振指标没有明显恶化,在长期稳定度指标方面得到明显提升,提高三个量级;

2) 在实时驯服方面,最小二乘法基于平方和最小的准则,需要一段时间的数据采集拟合才比较准确,无法进行实时驯服;无偏滑动平均滤波随窗口的向前滑动可随窗口的滑动进行实时驯服;卡尔曼滤波利用“预测-实测-修正”反复递推迭代方式,在实时驯服方面最具优势;

3) 在驯服时间方面,卡尔曼滤波能使数据快速收敛,驯服时间最短;无偏滑动平均滤波则需等一个窗口值测量完毕才能进行驯服;最小二乘法实现驯服时间最长;

4) 在守时能力方面,卡尔曼滤波算法能对下一步测量进行预测守时能力最好,而最小二乘法,无偏平均滑动滤波两种方法只能根据信号中断前得测量值进行守时,效果不明显。

5 结束语

本文分析了基于GNSS的晶振驯服技术工作原理,对比分析了最小二乘法、无偏滑动平均滤波法、卡尔曼滤波法三种主要的晶振驯服方法,并对这些方法进行了仿真实验,在实际运用方面进行了比较,给出了几种方法的优缺点,目前卡尔曼滤波法由于其在滤除噪声、守时方面具有优势运用较为广泛。本文可以为驯服晶振在GNSS授时接收机的应用提供一定的技术借鉴。

[1] 贺洪兵. 基于GPS 的高精度时间同步系统的研究设计[D]. 成都: 四川大学, 2005.

[2] 孙江涛.基于GPS的1PPS的二级频标驯服技术[D].西安：西安电子科技大学,2010.

[3] 向为,徐博,牟卫华, 等. 基于锁相环的GNSS授时接收机钟差校准算法[J].国防科技大学学报, 2013, 35(2): 115-119.

[4] 马煦,孔维,孙海燕.基于GPS驯服时钟的频率校准系统的设计[J].电讯技术,2011,51(10):109-112.

[5] 张杰,周栋明. GPS驯服中无偏滑动平均滤波算法的研究[J].电子学报,2013,41(2):412-416

[6] 樊多盛,施韶华,李孝辉. 基于GPS 接收机的铷原子钟驾驭方法研究[J], 电子测量与仪器学报,2013,27(10):980-984.

[7] 崔保健,王玉珍. GPS 驯服铷钟频标数据处理方法研究[J]. 电子测量与仪器学报,2010,24 (9):808-813.

[8] 范文晶. 基于 GPS 信号锁定二级频标技术的研究与实现[D]. 西安:西安电子科技大学, 2010.

AnalysisofDisciplinedCrystalOscillatorMethodBasedonGNSS

XUEYicong,GONGHang,LIUZengjun,ZHUXiangwei

(SatelliteNavigationR&DCenter,NationalUniv.ofDefenseTechnology,Changsha410073,China)

Contrast to the huge demand in measurement and testing, monitoring and communication, telecommunications and electricity and finance, a standard frequency source of high stability and high precision is crucial. GNSS disciplined crystal oscillator has combined the advantages of GNSS pulse per second signal which has good long-term stability and OCXO (Oven controlled crystal oscillators)which has good short-term stability. So GNSS disciplined crystal oscillator is widely applied for its high precision and low cost. In this paper, least squares algorithm, unbiased moving average filtering and Kalman filtering have been analyzed and compared.Those main filtering methods was applied to crystal oscillators which controlled in the same way.Their advantages and shortcomings have also been summed in this paper. Some meaningful suggestions are provided for the use of disciplined crystal oscillator in GNSS timing receiver.

GNSS; disciplined crystals oscillator; Least Square; Kalman filtering

10.13442/j.gnss.1008-9268.2017.04.007

P228.4

A

1008-9268(2017)04-0038-05

2017-03-10

联系人: 薛毅聪 E-mail: xueyicong123@163.com

薛毅聪(1986-)，男，硕士研究生，主要从事GNSS时频基准生成与测量技术研究。

龚航(1984-)，男，博士，讲师，主要从事GNSS时间同步与时间频率系统技术研究。

刘增军(1982-)，男，博士，讲师，主要从事卫星导航系统研究。

朱祥维(1980-)，男，博士，硕士生导师，副研究员，主要从事卫星导航系统研究。