BeSiN2和MgSiN2晶体稳定性和电子结构的第一性原理研究

王克龙，高尚鹏

(复旦大学 材料科学系，上海 200433)

BeSiN2和MgSiN2晶体稳定性和电子结构的第一性原理研究

王克龙，高尚鹏

(复旦大学 材料科学系，上海 200433)

自然条件下，BeSiN2和MgSiN2以正交晶系(α相)存在.施加压力之后，这两种材料会产生新的相(分别记作β相，γ相和δ相).运用密度泛函理论对材料的晶格参数进行了模拟；使用线性响应函数方法(密度泛函微扰理论)计算了材料的声子色散关系，得出：在无外界压力时，γ-BeSiN2，δ-BeSiN2和γ-MgSiN2结构不稳定，而其余各相可以稳定存在.运用密度泛函理论(分别使用PBE泛函和HSE泛函)得到其能带结构：其中β-BeSiN2和β-MgSiN2具有直接带隙，而其他6种相都是间接带隙；之后运用多体微扰理论框架下的GW方法对BeSiN2和MgSiN2布里渊区高对称点的能量值进行了修正；其中α-MgSiN2的带隙宽度为5.55eV，和实验值5.6eV吻合.

能带结构；BeSiN2；MgSiN2；声子色散；GW方法

碱土金属元素与氮化硅陶瓷的键合机制[1]以及碱土金属硅氮化合物(MSiN2，M=Be，Mg，Ca)的光学性能[2]近年来受到关注.碱土金属硅氮化合物可用于发光二极管中的荧光转换[2].MSiN2材料具有耐高温、化学稳定、高热导率、高硬度等优良的性质[3].自然条件下，BeSiN2和MgSiN2以一种类似于纤锌矿结构(α相)的形式存在，可以看作III族氮化物中的Al/Ga/In元素被II族的Be/Mg和IV族的Si取代.

Römer等[4]对碱土金属的硅氮化合物进行了系统的研究，通过比较焓值的大小对其高压下可能存在的结构进行了探索.在76GPa时，α相BeSiN2转化为一种体心立方结构(γ相)；在常压下，另外一种体心立方结构(β相)和α相的焓值相差很小(小于0.01eV).在25GPa时，MgSiN2由α相转化为三方晶系结构(δ相).此后，Boer等[5]对α-MgSiN2的能带结构做了研究.他们分别使用赝势平面波方法和全电子势方法对能带结构进行计算；使用X射线发射光谱(X-ray Emission Spectra,XES)对禁带宽度和电子态密度进行了测量，得到禁带宽度为(5.6±0.2)eV.Råsander等[6]使用赝势平面波方法，运用不同的交换关联势(局域密度近似和广义梯度近似)对α相和δ相MgSiN2的晶体参数和电子结构进行了计算.

使用局域密度近似和广义梯度近似时，密度泛函理论在计算激发态相关性质的时候存在明显的低估.采用HSE(Heyd-Scuseria-Ernzerhof)杂化泛函要求较大的计算量，却能得到更加精确的能带结构.而使用多体微扰理论框架下的GW方法也可以准确的预测禁带宽度等能带特征，可广泛的应用于碱金属、碱土金属、过渡金属、半导体和绝缘体、表面态等领域[7].

1 计算方法

1.1晶格优化

使用ABINIT[8-9]软件进行晶格优化.赝势选择投影缀加平面波(Projector Augmented Wave,PAW)方法，交换关联势选择为广义梯度近似中的PBE(Perdew-Burke-Ernzerhof)[10]，自洽计算的能量收敛判据选择为10-9Hartree.倒空间网格划分采用Monkhorst-Pack方法：α-BeSiN2为3×3×3，β-BeSiN2为4×4×4，γ-BeSiN2为4×4×4，δ-BeSiN2为6×6×6；α-MgSiN2为3×3×3，β-MgSiN2为4×4×4，γ-MgSiN2为4×4×4，δ-MgSiN2为6×6×6.晶格优化方法选择为BFGS(Broyden-Fletcher-Goldfarb-Shanno)拟牛顿算法.截断能设置，BeSiN2：40Hartree；MgSiN2：50Hartree.其中能量单位1Hartree=27.21eV.

1.2声子色散谱计算参数

声子性质的计算采用Quantum Espresso[11]软件包.自洽计算选择的赝势方法为模守恒[12]的Troullier-Martins赝势.该赝势在原子的截断半径内使用泰勒级数对全电子势进行模拟，保证了在截断半径处赝势和全电子势的零阶到四阶导数一致性，该赝势既比真实势光滑，计算上更加方便，又保证了电子波函数一定的精确性.交换关联势也是PBE.截断能设置，BeSiN2：30Hartree；MgSiN2：35Hartree.Monkhorst-Pack倒空间网格划分的参数：α-BeSiN2为4×4×4，β-BeSiN2为6×4×4，γ-BeSiN2为6×4×4，δ-BeSiN2为8×4×4；α-MgSiN2为4×4×4，β-MgSiN2为6×4×4，γ-MgSiN2为6×4×4，δ-MgSiN2为8×4×4.声子的振动频率首先在所划分的网格上进行计算，得到原子间作用力常数矩阵(Matrix of Interatomic Force Constants)之后，再对色散谱中布里渊区各点进行计算.

1.3电子能带结构计算参数

使用ABINIT进行能带计算.首先用密度泛函理论对上述5种结构进行能带计算.使用的晶格参数是理论优化得到的数值.所计算的能带数分别是：α-BeSiN2为60，β-BeSiN2为36，γ-BeSiN2为36，δ-BeSiN2为20；α-MgSiN2为60，β-MgSiN2为36，γ-MgSiN2为36，δ-MgSiN2为20.选用的晶胞均为原胞(primitive cell).各结构晶胞所含的原子数分别为：α相为16，β相为8，γ相为8，δ相为4.赝势构造方法为PAW，交换关联泛函选择为PBE.截断能和倒空间网格划分方式与计算晶格常数时一致.

作为比较，又采用HSE泛函进行了计算.赝势类型选择为模守恒.截断能设置，BeSiN2：26Hartree；MgSiN2：33Hartree.倒空间网格划分：α-BeSiN2为3×2×3，β-BeSiN2为4×4×5，γ-BeSiN2为4×4×5，α-MgSiN2为3×2×3，δ-MgSiN2为5×5×5.

然后运用多体微扰理论对布里渊区高对称点的能级进行修正.α相属于正交晶系，高对称点包括Г-Z-T-Y-S-X-U-R；β相和γ相属于体心四方晶系，高对称点包括Z-Г-X-P-N；δ相属于三方晶系，高对称点包括F-Г-Z-L.α-BeSiN2的Monkhorst-Pack网格划分为4×4×4，修正的能带数是第35到38条.β-BeSiN2和γ-BeSiN2的倒空间网格划分为4×4×4，修正的能带数是第17到20条.δ-BeSiN2的倒空间网格划分为6×6×6，修正的能带数是第8到11条.α-MgSiN2的倒空间网格划分为4×4×4，修正的能带数是第47到50条.β-MgSiN2和γ-MgSiN2的倒空间网格划分为4×4×4，修正的能带数是第23到26条.δ-MgSiN2的倒空间网格划分为6×6×6，修正的能带数是第11到14条.

2 结果与讨论

2.1晶格参数

对于BeSiN2和MgSiN2两种材料，α相和β相存在一定的相似性：二者的M(M=Be，Mg)原子位于氮原子构成的四面体中心，硅原子也位于氮原子构成的四面体中心.而γ相的M原子和硅原子都位于6个氮原子构成的八面体中心，该结构类似于NaCl结构.δ相的M原子和硅原子也被6个氮原子包围，成为八面体中心.BeSiN2和MgSiN2的晶胞结构见图1(见第580页).

表1和表2(见第580页)给出了BeSiN2和MgSiN2的晶体学参数.各结构的第1行晶格常数为本研究得到的结果，使用的交换关联势是广义梯度近似(General Gradient Approximation,GGA)；第2行是Römer等使用局域密度近似(Local Density Approximation,LDA)得到的结果.α-BeSiN2和α-MgSiN2天然存在，其晶格常数的实验值分别列于第3行.最右边的两列分别是各个结构的空间群号和各原子具体的Wyckoff位置.

对比BeSiN2和MgSiN2同一相的晶格参数可以得到，BeSiN2的晶格参数值较小.比如α-BeSiN2的x轴长度为4.995Å，α-MgSiN2的x轴长度为5.306Å.这是由于Be原子比Mg原子半径要小一些，使得Be-N键长比Mg-N键长小.

图1 MSiN2的晶体结构示意图Fig.1 Crystal structures of MSiN2

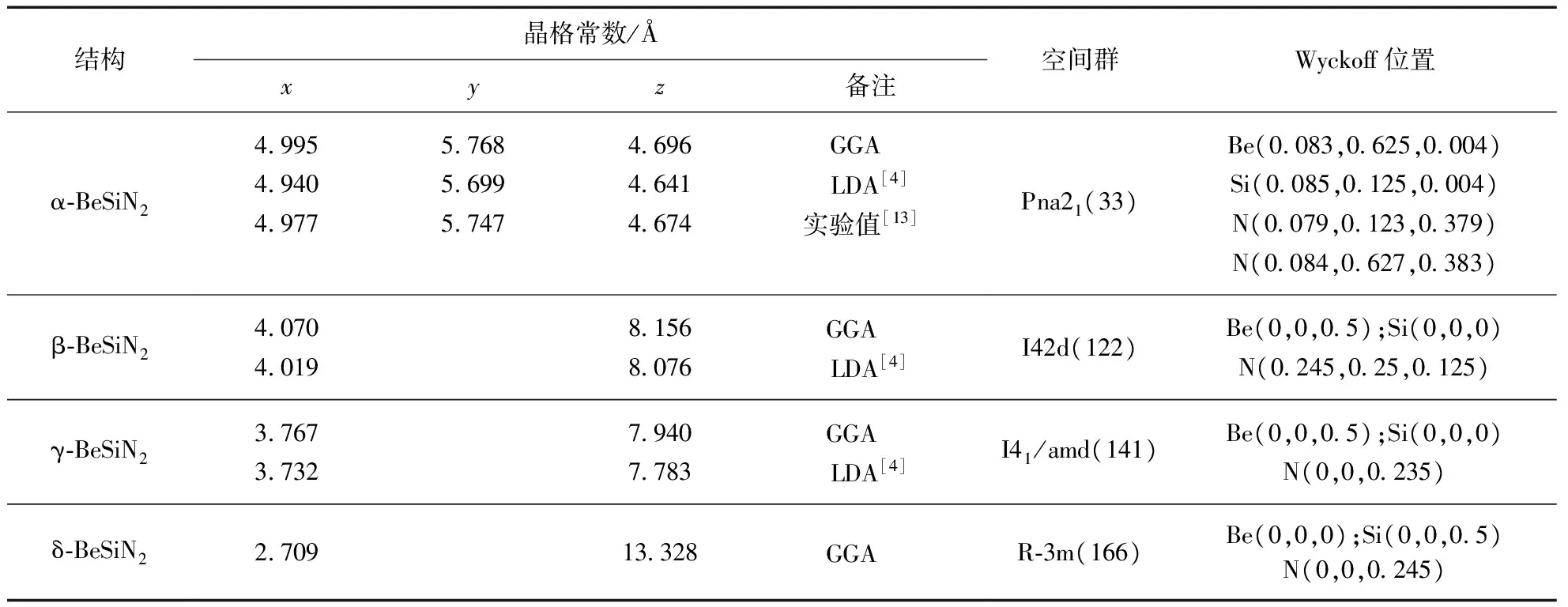
表1 BeSiN2的晶体学参数Tab.1 Crystal parameters of BeSiN2

表2 MgSiN2的晶体学参数Tab.2 Crystal parameters of MgSiN2

对于α-BeSiN2和α-MgSiN2来说，使用GGA得到的晶格常数比实验值普遍偏大，和经验上的GGA结果相符，这是由于GGA有使得化学键伸展的趋势；本研究中理论值和实验值的误差在0.3%到0.7%之间.而使用LDA常常会使得晶格参数的计算值偏小：其误差在0.9%以内.在BeSiN2和MgSiN2的体系中，只有δ-MgSiN2的z轴长度在使用LDA时比实验值偏大，其计算结果为4.995Å，而实验值为4.992Å.因此使用密度泛函理论对晶格参数的计算较为精确.而晶格优化能够快速收敛也得益于BFGS拟牛顿算法能够在减小计算量的同时保证精确性.

2.2声子色散谱和结构稳定性

通过计算各晶体的声子色散谱可以判断其结构稳定性.图2和图3(见第582页)给出了各相的声子谱图.左边红线表示布里渊区内声子的振动频率，右边绿线表示声子的态密度(Phonon Density of States,Ph-DOS).α-BeSiN2和β-BeSiN2的声子不存在虚频；而γ-BeSiN2和δ-BeSiN2存在虚频.因此α-BeSiN2和β-BeSiN2可以稳定存在，而γ-BeSiN2和δ-BeSiN2不能稳定存在.α-MgSiN2，β-MgSiN2，δ-MgSiN2的声子谱都不存在虚频，在无外界压力时能稳定存在.γ-MgSiN2存在严重的虚频，达到了-400cm-1，不稳定.

图2 BeSiN2的声子色散Fig.2 Phonon dispersion of BeSiN2

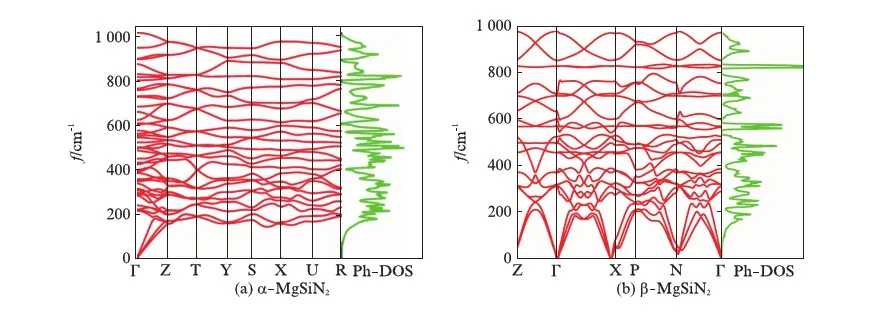
图3 MgSiN2的声子色散Fig.3 Phonon dispersion of MgSiN2

通过比较不同相的焓值也可以得到其相对稳定性结果：

H=E+PV，

其中：H为焓值；E为体系能量；P为压强；V是体积.

在压强为零时，焓值等于能量值，因此可以通过比较总能(total energy)来确定相对稳定性.使用PAW赝势和GGA交换关联泛函对各相的总能进行了计算.

表3 BeSiN2和MgSiN2的总能Tab.3 Total energy of BeSiN2and MgSiN2

根据表3中的数据，α-BeSiN2和β-BeSiN2的总能值十分接近，其差别小于0.01eV.因此β-BeSiN2在无外界压力下时是稳定的.而γ-BeSiN2的总能值比α-BeSiN2高出2.07eV，该数值可以表明其不稳定.δ-BeSiN2的总能值比α-BeSiN2高出2.51eV，其在零压力时也不稳定.Römer等通过计算高压下各相焓值，得到在临界压强76GPa时，α-BeSiN2和γ-BeSiN2的焓值产生交叠，发生相变.

β-MgSiN2和基态(α-MgSiN2)的能量值仅相差0.19eV，可以稳定存在.γ-MgSiN2和基态的能量值相差1.78eV，在零压时不稳定.δ-MgSiN2和基态的能量值相差1.12eV，属于亚稳态.Råsander等得到：在20GPa时，α-MgSiN2和δ-MgSiN2的焓值达到一致；高于20GPa时，δ-MgSiN2焓值逐渐低于α-MgSiN2的焓值.

对比上述总能的结果与声子谱的结果，可以得出β-BeSiN2，β-MgSiN2和δ-MgSiN2在零压时可以稳定存在；而γ-BeSiN2，δ-BeSiN2和γ-MgSiN2在零压时不稳定.

2.3电子能带结构

材料对光的吸收及发射和电子的能量跃迁相关，通过计算其能带结构可以得到丰富的信息.首先运用密度泛函理论(Density Functional Theory,DFT)进行能带计算，然后用多体微扰理论的GW近似(格林函数G与库伦屏蔽作用W)对高对称点的能量值进行修正.表4给出了使用GW近似得到的价带顶和导带底的布里渊区点和能量值.8种结构的禁带宽度处于4到7eV之间，属于宽禁带半导体，其能量对应的光波位于中紫外区.β-BeSiN2和β-MgSiN2是直接带隙，另外6种结构为间接带隙.

α-MgSiN2的实验值是(5.6±0.2)eV，和GW的结果一致(5.55eV)，而GGA得到的结果是3.98eV，误差为29%.使用HSE泛函得到的值为5.32eV，比实验值小0.3eV.运用全电子势和GGA得到的禁带宽度4.17eV，和赝势方法计算结果相比，并没有显著地提高精度.

使用DFT-GGA的禁带宽度值均比GW近似的结果小，二者的偏差在1.2到1.7eV之间.使用DFT-HSE得到的禁带宽度值和GW的结果十分接近，对于本研究中的材料来说，二者的差异均小于0.23eV.对于δ-MgSiN2，Råsander等使用HSE泛函和PAW势得到的禁带宽度为5.87eV[6]，这和GW的结果5.76eV非常接近，而本研究中使用HSE和模守恒势得到的结果是5.86eV.

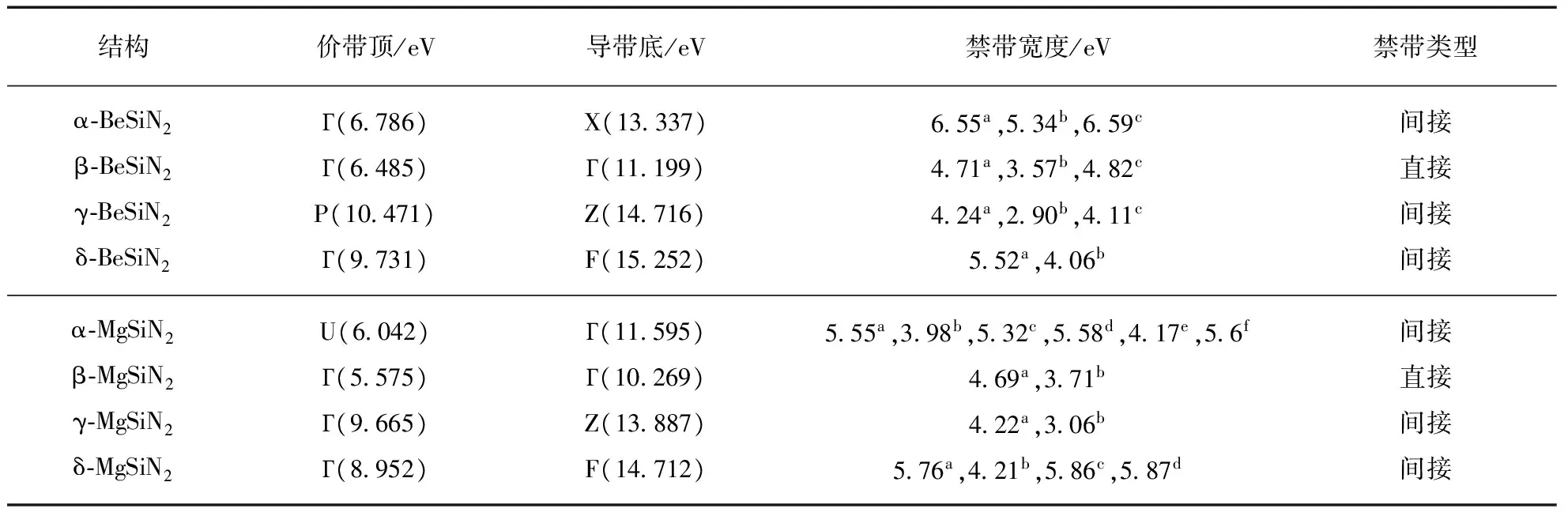
表4 BeSiN2和MgSiN2的禁带宽度Tab.4 Band gap of BeSiN2 and MgSiN2

a本研究的结果：GW近似；b本研究的结果：密度泛函理论，GGA-PBE泛函，PAW势；c本研究的结果：密度泛函理论，HSE杂化泛函，模守恒势；d文献[6]：密度泛函理论，HSE杂化泛函，PAW势；e文献[5]：密度泛函理论，GGA-PBE泛函，全电子势；f文献[5]：实验值.

通过对BeSiN2和MgSiN2进行横向比较，可以发现二者在具有相同结构时拥有较为接近的禁带宽度.比如β-BeSiN2禁带宽度为4.71eV，β-MgSiN2禁带宽度为4.69eV，仅相差0.02eV.γ相的两种材料禁带宽度也是相差0.02eV，δ相的相差0.24eV.只有α相的相差较大：α-BeSiN2比α-MgSiN2高出1.00eV.对于两种材料，均只有β相是直接带隙半导体.

观察图4和图5(见第584页)可以更加直观地得到能带信息.实线表示使用DFT-GGA得到的能带，小方块◆是运用GW修正之后的能带值，所修正的是能量最低的2条导带数值和能量最高的2条价带.图中多处GW修正值在价带处只有一个值，这表示能量最高的2条价带是简并的.

可以看出，在价带上，DFT-GGA和GW的结果很接近.如对于α-BeSiN2，使用DFT-GGA得到的价带顶数值为6.63eV，而GW值为6.78eV，差异为0.15eV，其他各结构也是如此：使用两种计算方法得到的价带的结果差异在0.2eV以内.但是导带的情况却不一样.从图中可以明显看出导带的方块点(GW值)比导带的实线(DFT-GGA值)高出1到2eV.比如对于α-BeSiN2来说，其导带底的DFT-GGA结果是11.76eV，其GW结果为13.33eV，相差1.57eV.但是两种方法在计算极值点的位置时得到的结果是一致的，因此得到的禁带类型(直接带隙或间接带隙)也是一致的.通过对两种方法导带和价带结果的对比可以看出，采用GGA交换关联能的密度泛函理论在计算基态能量时可以取得精确的结果，但在计算激发态能量时误差较大(1～2eV).

图4 BeSiN2的电子能带结构Fig.4 Electronic band structures of BeSiN2

图5 MgSiN2的电子能带结构Fig.5 Electronic band structures of MgSiN2

3 结 论

本研究运用密度泛函理论对BeSiN2各相和MgSiN2各相的总能值进行了比较，并运用响应函数方法对其声子谱做了计算.结果表明：无外界压力时，α-BeSiN2、β-BeSiN2、α-MgSiN2、β-MgSiN2、δ-MgSiN2是稳定存在的；γ-BeSiN2、δ-BeSiN2和γ-MgSiN2是不稳定的.使用DFT-GGA对材料的晶格常数做了计算，得到的晶格参数与实验值相比误差小于0.7%.同一结构的BeSiN2比MgSiN2晶格参数小.运用DFT-GGA，DFT-HSE和GW方法分别计算了能带结构.其中由DFT-GGA方法计算得到的禁带宽度比实验值偏小，对于α-MgSiN2来说，误差为29%；由DFT-HSE方法计算得到的禁带宽度结果为5.32eV，误差小于5%；而由GW计算得到的结果为5.55eV，和实验值(5.6±0.2)eV一致.由此可以比较上述3种方法在计算能带结构时的特点：DFT-GGA和实验值相差较大(30%左右)；GW和DFT-HSE结果精确(误差5%以内).对于本研究中的体系，运用DFT-HSE得到的禁带宽度值和GW近似的结果十分接近，二者之间的差别均小于0.23eV.同一结构的BeSiN2和MgSiN2禁带类型一致，禁带宽度较为接近(均小于1.0eV).

[1] ZIEGLER A,IDROBO J,CINIBULK M K,etal.Interface structure and atomic bonding characteristics in silicon nitride ceramics [J].Science,2004,306(5702)：1768-1770.

[2] MUELLER-MACH R,MUELLER G,KRAMES M R,etal.Highly efficient all-nitride phosphor-converted white light emitting diode [J].PhysicaStatusSolidi(a),2005,202(9)：1727-1732.

[3] NORDBERG L O,NYGREN M,KLL P O,etal.Stability and oxidation properties of RE-α-sialon ceramics (RE=Y,Nd,Sm,Yb) [J].JournaloftheAmericanCeramicSociety,1998,81(6)：1461-1470.

[4] RÖMER S R,KROLL P,SCHNICK W.A density functional study of the high-pressure chemistry of MSiN2(M=Be,Mg,Ca)：Prediction of high-pressure phases and examination of pressure-induced decomposition [J].JournalofPhysics：CondensedMatter,2009,21(27)：275407.

[5] BOER T,BOYKO T D,BRAUN C,etal.Band gap and electronic structure of MgSiN2determined using soft X-ray spectroscopy and density functional theory [J].PhysicaStatusSolidi-RapidResearchLetters,2015,9(4)：250-254.

[7] ARYASETIAWAN F,GUNNARSSON O.The GW method [J].ReportsonProgressinPhysics,1998,61(3)：237.

[8] GONZE X,AMADON B,ANGLADE P,etal.ABINIT：First-principles approach to material and nanosystem properties [J].ComputerPhysicsCommunications,2009,180(12)：2582-2615.

[9] GONZE X,JOLLET F,ARAUJO F A,etal.Recent developments in the ABINIT software package [J].ComputerPhysicsCommunications,2016,205：106-131.

[10] PERDEW J P,BURKE K,ERNZERHOF M.Generalized gradient approximation made simple [J].PhysicalReviewLetters,1996,77(7)：3865.

[11] GIANNOZZI P,BARONI S,BONINI N,etal.QUANTUM ESPRESSO：A modular and open-source software project for quantum simulations of materials [J].JournalofPhysics：CondensedMatter,2009,21(39)：395502.

[12] HAMANN D,SCHLÜTER M,CHIANG C.Norm-conserving pseudopotentials [J].PhysicalReviewLetters,1979,43(20)：1494.

[13] ECKERLIN P.Zur Kenntnis des Systems Be3N2-Si3N4,IV.Die Kristallstruktur von BeSiN2[J].ZeitschriftFürAnorganischeUndAllgemeineChemie,1967,353(5-6)：225-235.

[14] WINTENBERGER M,TCHEOU F,DAVID J,etal.A refinement of the structure of the nitride MgSiN2：A study by neutron diffraction [J].ZeitschriftFürNaturforschungB,1980,35(5)：604-606.

FirstPrincipleStudiesontheStabilityandElectronicStructuresofBeSiN2andMgSiN2

WANGKelong,GAOShangpeng

(DepartmentofMaterialsScience,FudanUniversity,Shanghai200433,China)

BeSiN2and MgSiN2own potential applications in luminescence.Naturally,they exist in orthorhombic crystals (α phase).Under external pressure,both of them transform into new phases (β,γ and δ phase).Lattice parameters of BeSiN2and MgSiN2polymorphs are calculated by employing density functional theory.Phonon dispersions are obtained by linear response functions (density functional perturbation theory).γ-BeSiN2,δ-BeSiN2and γ-MgSiN2are dynamically unstable,while all the other phases are stable at ambient pressure.Band structures are calculated by employing both PBE and HSE functional,results indicate that only β-BeSiN2and β-MgSiN2have direct band gaps among 8 phases.Band energies at high symmetry points in Brillouin zone are corrected by many-body perturbation theory.α-MgSiN2has an indirect band gap of 5.55 eV,which is close to experimental result 5.6 eV.

band structure; BeSiN2; MgSiN2; phonon dispersion; GW method

0427-7104(2017)05-0578-08

2017-04-19

上海市教育委员会科研创新项目(15ZZ001)；上海市科学技术委员会科研计划项目(14521100606)

王克龙(1992—)，男，硕士研究生，通信联系人，E-mail：14210300011@fudan.edu.cn.

O471.5

A