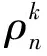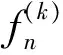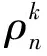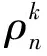分担连续函数的全纯函数正规族
2017-11-09刘芝秀李运通黄小杰
刘芝秀,李运通,黄小杰
(1.南昌工程学院 理学院,南昌 330099;2.陕西铁路工程职业技术学院 教务处,渭南 714000)
分担连续函数的全纯函数正规族
刘芝秀1,李运通2,黄小杰1
(1.南昌工程学院 理学院,南昌 330099;2.陕西铁路工程职业技术学院 教务处,渭南 714000)
研究了分担连续函数的全纯函数族的正规性问题,推广了一些已有的结论.设F为定义在区域D上的全纯函数族,h1,h2为两个连续函数满足对∀z∈D有h1(z)≠h2(z),并设k≥2为正整数.若∀f∈F,有f(z)=hi(z)⟹|f(k)(z)|≤|hi(z)|,i=1,2,则F为D上的正规族;并举例说明了k=1时,结论不成立.此外,还将分担值条件用拓扑度条件代替得到了一个涉及拓扑度条件的全纯函数族正规定则.
正规族;全纯函数;值分布;拓扑度
1 引言和主要结果
本文继文献[1]后用拓扑度理论研究了分担连续函数的全纯函数族的正规性问题,有关值分布和正规族等方面的概念结论详见文献[2-4],下面仅扼要介绍正规族、分担值和拓扑度的概念及记号.
设D为平面区域,F为D上的亚纯函数族,若对任意的函数列{fn}⊂F存在子列在D上局部一致收敛于一亚纯函数或局部一致趋于∞,则称F是D上的正规族.
设f(z),g(z),a(z)均为D上的函数,若f(z)-a(z)=0,必有g(z)-a(z)=0,则记为f(z)=a(z)⟹g(z)=a(z).所以,若f(z)-a(z)和g(z)-a(z)有相同的零点,则可记为f(z)=a(z)⟺g(z)=a(z),称f(z)与g(z)IM分担a(z).
有关拓扑度的概念详见文献[5],设M为形式(f;U;y)的集合,这里U为中的有界开区域,f:U→为一连续函数,yf(∂U),则存在一确定的整值函数d:M→满足一定的条件,此函数d:M→称为拓扑度.特别地,若f为一非常数全纯函数,则d(f;U;0)为f(∂U)围绕0的回转数.
Schwick[6]首先把分担值与正规族联系起来并证明了定理A.
定理A[6]设F为区域D上的亚纯函数族,a1,a2,a3为3 个相互判别的有穷复数.若∀f∈F,f(z)=ai⟺f′(z)=ai,i=1,2,3,则F为D上的正规族.
近年来,不少学者研究此类问题产生了许多新方法与技巧,并导出了很多结果与新问题.例如,关于分担函数的正规族问题,Pang等[7],Lü等[1]证明了下列结论.
定理B[7]设F为定义在区域D上的全纯函数族,h(z)为不恒为0的全纯函数.若∀f∈F,f(z)=0⟹f′(z)=0且f′(z)≠h(z),则F为D上的正规族.
定理C[1]设F为定义在区域D上的全纯函数族,设h1,h2为两个连续函数满足h1(z)≠h2(z)对任意z∈D.若∀f∈F,有f(z)=h1(z)⟹f′(z)=h1(z)和f(z)≠h2(z),则F在D上正规.
定理D[1]设F为定义在区域D上的全纯函数族,设h1,h2,h3为3个连续函数满足对∀z∈D,hi(z)≠hj(z),i≠j.若∀f∈F,有f(z)=hi(z)⟹f′(z)=hi(z),i=1,2,3,则F为D上的正规族.
本文推广了上述定理,证明了下面的结论.
定理1设F为定义在区域D上的全纯函数族,h1,h2为两个连续函数满足对∀z∈D,h1(z)≠h2(z),并设k≥2为正整数.若∀f∈F,有f(z)=hi(z)⟹|f(k)(z)|≤|hi(z)|,i=1,2,则F为D上的正规族.
注1定理1中条件k≥2是不能去掉的,因为当k=1时定理1的结论是不成立的,下面的例子说明了这个事实.
例1设D为单位圆,令h1(z)=ez,h2(z)=-ez,且fn(z)=ezsin(nz),n=1,2,….则

但是{fn}在z=0不正规.

注2类似定理1的证明,定理C中的条件f(z)=h1(z)⟹f′(z)=h1(z)可以减弱为f(z)=h1(z)⟹|f′(z)|≤|h1(z)|.
由于全纯函数的拓扑度d(f;U;0)为f(∂U)围绕0的回转数,再注意到辅角原理则可以考虑把分担值条件用拓扑度条件来代替.
定理2设F为定义在区域D上的全纯函数族,设h1,h2为两个连续函数满足h1(z)≠h2(z)对任意z∈D,k≥1为正整数,假设下述条件成立.
(i) 对任意区域Δ,常数ρ,b和任意f∈F,若ρz+b∈D对任意z∈Δ,有
d(f(ρz+b)-h1(ρz+b);Δ;0)=d(f(k)(ρz+b)-h1(ρz+b);Δ;0),
这里d(f;Δ;0)为拓扑度;
(ii)
f(z)=h2(z)⟹|f(k)(z)|≤|h2(z)|.
则F为D上的正规族.
注3由定理2的证明方法可以看出,定理2中的条件(ii)同样可以用拓扑度条件d(f(ρz+b)-h2(ρz+b);Δ;0)=d(f(k)(ρz+b)-h2(ρz+b);Δ;0)一同代替掉,F仍然为正规族.
2 几个引理
为了证明定理,首先给出下述引理.
引理1[8]设F为定义在区域D上的亚纯函数族,若F在z0∈D不正规,则存在
(a) 点列zn∈D,zn→z0;
(b) 函数列fn∈F;
(c) 正数点列ρn→0.
满足fn(zn+ρnξ)=gn(ξ)→g(ξ)局部一致收敛,其中g为一非常数亚纯函数.
引理2[5]拓扑度函数满足下列性质:
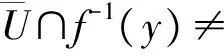
Hurwitz定理在亚纯函数正规族证明中往往能起重要的作用,但是,对于连续函数,此定理不成立,不过有类似Hurwitz定理作用的下述引理.
引理3设fn(n=1,2,…)为一连续函数列,在D局部一致收敛于一个连续函数f,若d(f,Uz0,w)≠0,{Uz0}是z0的邻域基,则存在一数列{nk}⊆+和一点列znk满足znk→z0且fnk(znk)=w.
证 设Ur={z||z-z0| d(fn;Ur;w)=d(f;Ur;w)≠0. 注4[1]特别地,若f是一个非常数全纯函数且f(z0)=0,则可得d(f;Ur;0)为f(∂Ur)围绕0的回转,由辐角定理可得d(f;Ur;0)为f在Ωr取0值的次数.故d(f;Ur;0)≠0,那么存在一个数列{nk}⊆+和一点列znk满足znk→z0且fnk(znk)=0. 注5下列例子说明了引理3(注4)中条件d(f,Uz0,w)≠0(f为全纯函数)是必须的. 假设F在z0不正规,则根据引理1,可选择函数列(fn)⊆F,数列(zn)和正数列(ρn)满足zn→z0,ρn→0和 gn(ζ)=fn(zn+ρnζ)→g(ζ) (1) (2) 和 Hn(ζ)=fn(zn+ρnζ)-h1(zn+ρnζ)→g(ζ)-h1(z0)=H(ζ) (3) 接下来,将证明g(ζ)-h1(z0)仅有至少k+1重零点. 假设H(ζ0)=g(ζ0)-h1(z0)=0.注意到Hn→H在局部一致收敛和引理3的注4,则存在子列{ζn}满足ζn→ζ0和(对足够大的n) Hn(ζn)=fn(zn+ρnζn)-h1(zn+ρnζn)=0. 它表明g(ζ)-h1(z0)仅有至少k+1重零点.类似地,可得g(ζ)-h2(z0)仅有至少k+1重零点. 综合hi(z0)≠hj(z0)(i≠j)和第二基本定理,有 矛盾.故定理1得证. 假设F在z0不正规,则根据引理1,可选择函数列(fn)⊆F,数列(zn)和正数列(ρn)满足zn→z0,ρn→0和 gn(ζ)=fn(zn+ρnζ)→g(ζ) (4) Hn(ζ)=fn(zn+ρnζ)-h1(zn+ρnζ)→g(ζ)-h1(z0)=H(ζ) (5) 和 (6) 因H为整函数,所以由辐角定理可得d(H;Δr;0)等于H在Δr上的零点个数,即d(H;Δr;0)=p.注意到fn(zn+ρnζ)-h1(zn+ρnζ)→H(ζ)在局部一致收敛,可得(当n足够大) d(fn(zn+ρnζ)-h1(zn+ρnζ);Δr;0)=d(H;Δr;0)=p. 通过假设(i)得 显然 另外,应用定理1的方法,可证g(ζ)-h2(z0)仅有k+1重零点. 进而,应用第二基本定理可得 矛盾.故定理2得证. [1] LÜ F,ZHOU F.A new study on normal families concerning continuous functions [J].ActaMathematicaScientia,2014,34A(6):1348-1352. [2] GU Y X,PANG X C,FANG M L.Normal families and its application [M].Beijing: Science Press,2007. [3] YI H,YANG C.Uniqueness theory of meromorphic functions [M].Beijing:Science Press,1995. [4] YANG L.Value distribution theory [M].Berlin:Springer-Verlag,1993. [5] DEIMLING K.Nonlinear functional analysis [M].New York: Spring-Verlag,1985. [6] SCHWICK W.Sharing values and normality [J].ArchMath,1992,59(2):50-54. [7] PANG X C,FANG M L,ZALCMAN L.Normal families of holomorphic functions with multiple zeros [J].ConformalGeometry&DynamicsoftheAmericanMathematicalSociety,2007,11(8):101-106. [8] ZALCMAN L.Normal families:New perspectives [J].BullAmerMath,1998,35(3):215-230. NormalFamiliesofHolomorphicFunctionsSharingContinuousFunction LIUZhixiu1,LIYongtong2,HUANGXiaojie1 (1.CollegeofScience,NanchangInstituteofTechnology,Nanchang330099,China; 2.Dean’sOffice,ShaanxiRailwayInstitute,Weinan714000,China) It studies the normality of family of holomorphic functions sharing continuous function and extends some existing conclusions.LetFbe a family of holomorphic functions defined on domainD,h1,h2be two different continuous functions satisfied ∀z∈D,h1(z)≠h2(z),andk≥2 be a positive integer.If ∀f∈F,such thatf(z)=hi(z)⟹|f(k)(z)|≤|hj(z)|,i=1,2,thenFis a normal family; An example is given to explain that the conclusion does not hold whenk=1.In addition,a normal criterion concerning topological degree is also got by replacing shared value condition with topological degree condition. normal family;holomorphic function;value distribution;topological degree 0427-7104(2017)05-0533-04 2016-01-30 南昌工程学院青年基金 (2014KJ025);陕西铁路工程职业技术学院基金(2013-12) 刘芝秀(1982—),女,硕士研究生;黄小杰(1983—),男,博士,讲师,通信联系人,E-mail:359536229@qq.com. O174.52 A
3 定理1的证明
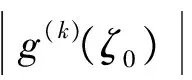
4 定理2的证明