基于支持向量机的脱硝效率预测模型研究
2017-11-09崔海波杨浩楠耿向瑾
崔海波, 杨浩楠, 耿向瑾, 李 斌, 邓 煜
(1. 云南电力试验研究院(集团)有限公司 动力研究所,云南 昆明 650217;2. 华北电力大学 能源动力与机械工程学院,河北 保定 071003)
基于支持向量机的脱硝效率预测模型研究
崔海波1, 杨浩楠2, 耿向瑾1, 李 斌2, 邓 煜2
(1. 云南电力试验研究院(集团)有限公司 动力研究所,云南 昆明 650217;2. 华北电力大学 能源动力与机械工程学院,河北 保定 071003)
脱硝效率受到众多关联性较强的因素影响,使得脱硝效率难以准确地实时测量。采用皮尔逊相关系数与反应机理结合的方法选取辅助变量,运用支持向量机建立以选取的辅助变量为输入脱硝效率为输出的预测模型。并基于某电厂脱硝系统实际运行数据对模型进行训练验证。结果表明:预测模型相关系数高达 99.897 9%,均方误差为6.574 68×10-5;大部分的样本点误差在-1.0~1.0之间,部分误差趋于0值,最大误差绝对值不超过1.8。说明该模型的预测精度较高,且具有良好的推广能力,能较好地满足工程实际需求。
脱硝效率; 皮尔逊相关系数; 反应机理; 支持向量机; 预测模型
0 引言
随着节能减排政策的大力推行,国家对氮氧化物排放的把控越发严格。在“十三·五”规划中,国家进一步限制了污染物的排放[1]。而“超低排放”政策的提出更是需要让火电厂优化改造脱硝系统。而国内各电厂机组已基本完成对脱硝系统的改造。目前我国火电厂使用最广泛的脱硝技术是选择性催化还原脱硝技术,该技术具有高脱除率、技术成熟、二次污染小等优点,是我国火电厂脱除NOx最有效的方法。
脱硝效率作为评价脱硝系统NOx脱除程度的主要评价指标,能够实时有效地评价脱硝系统运行性能。烟气连续排放检测系统(CEMS)是现阶段我国各火电厂主要使用的NOx排放检测设备。该系统可用来检测火电厂排放的NOx浓度从而可以计算出脱硝效率[2]。但是CEMS系统工作复杂,系统元件长时间工作会影响测量的准确性,另外昂贵的设备安装费用也会增加电厂的成本投资。由于我国的大部分燃煤火电厂,燃烧的煤成分比较稳定,为利用软测量技术间接测量NOx排放浓度提供了可能,所以针对脱硝效率监测的问题,部分学者提出利用软测量技术对脱硝效率进行预测分析[3-6]。他们利用多元回归算法、神经网络、遗传算法或偏最小二乘法等对脱硝效率进行建模预测,取得了较好的预测效果,但是由于辅助变量选取较少,数据样本偏少等原因,使得文献中预测结果仍然存在着较大的误差,同时缺乏一定的推广能力。而支持向量机作为软测量技术的一种,具有解决非线性问题预测精准、泛化性强等特点[7],该方法在工程实践中已经有许多的成功应用[8-14]。学者将支持向量机应用于燃烧效率预测与优化、变工况负荷预测以及飞灰含碳量预测等方面都取得了符合实际要求的结果。文献[15]比较了神经网络,偏最小二乘和支持向量机算法对脱硫效率预测的结果,说明支持向量机算法的预测结果更精准且更符合工程实际。综合以上原因,本文建立基于支持向量机的脱硝效率预测模型预测脱硝效率,并利用火电厂实际运行数据对模型进行训练验证和对预测结果进行分析。
1 支持向量机的建模原理
支持向量机是基于统计学理论的监督学习模型,最早在1995年由CorinnaCortes等人提出[16]。该算法采用结构风险最小原理和VC维理论对有限的样本在学习能力和模型的复杂性之间寻求最优点,从而获得最好推广能力。
1.1支持向量机建模原理
支持向量机可以被看做一种广义的线性分类器,其通过非线性变换将输入控件变换到一个高维的特征空间,并在新的空间中寻找最小的线性分界面。具体原理如图1所示。图1表示支持向量机分类模型,其中,两类圆点分别代表两类训练样本,x1、x2为样本的特征项,H为分界面,H1、H2分别表示平行于分界面H且过离分界面最近的样本点的平面。在该模型中,为了提高模型的泛化性和确保经验风险最小化,分界面在使两类样本点正确分离开的同时还要确保最大化两类样本点之间的分类间隔M。
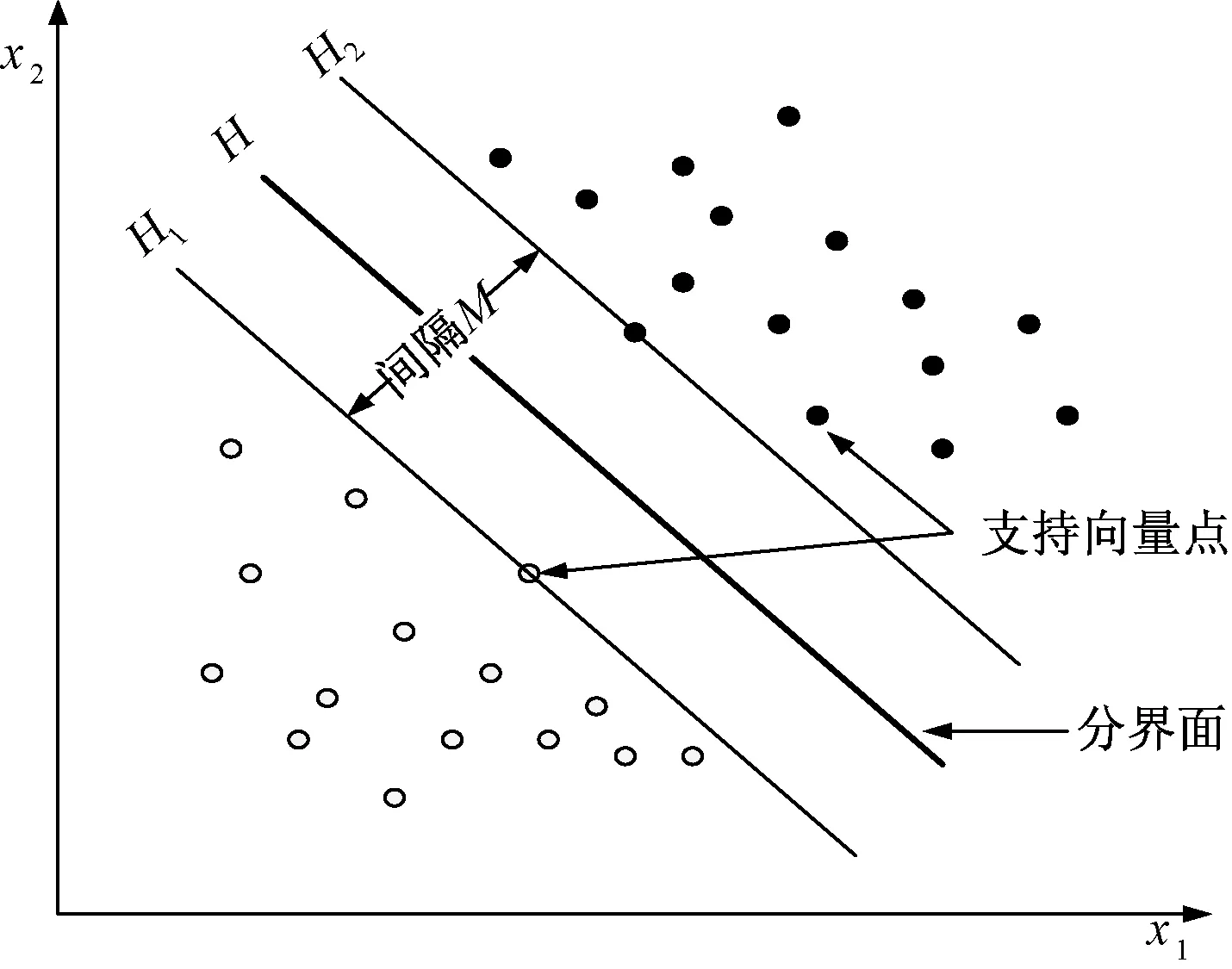
图1 支持向量机原理示意图
SVM模型的求解过程是将问题转换成为一个凸二次优化,在上面的理论分析中存在全局最佳点,有效地解决局部极值问题。下面对支持向量回归机进行简单的介绍。
假设给定训练集:
T={(x1,y1),…,(xl,yl)}∈(Rn×y)l
(1)
其中,xi∈Rn,yi∈y=R,i=1,…,l,据此寻找Rn上一个函数Φ(x),以便用y=Φ(x)来推断任一输入辅助变量x所对应的输出值y。
通过优化目标函数来实现对支持向量机目标函数的回归,优化模型如公式(2)与公式(3):
(2)
(3)

(4)
式中:K(xi,x)为核函数。本文算法中的回归函数是利用高斯径向基核函数(RBF)作为核函数来构建实现。其中:
K(xi,x)=exp(-γ||xi-x||2),γ>0
(5)
高斯径向基核函数可以使模型的精确度更高,将其运用在回归预测中有较好的预测效果,同时具有较好的推广能力。
1.2支持向量机参数选择
预测模型性能主要取决于核函数参数g和惩罚参数c这2个参数的选取。为了保证预测的准确性及模型的可行性,在选取合理的核函数的同时,也要合理的选取核函数参数g和惩罚参数c。本文采用交叉验证的方法实现对脱硝预测模型2个重要参数g和c的精确选取。将参数进行2次离散化筛选,分别为粗略筛选和精细筛选。先将范围都设定为2-8~28,参数c和g的步长设定为1,经过粗略筛选之后得到较优的核函数参数g和惩罚参数c为256和0.329 88。粗略筛选如图2所示。
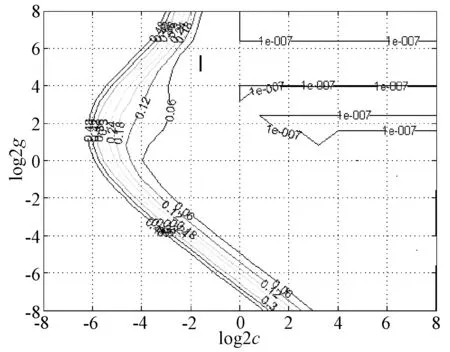
图2 脱硝参数粗略筛选等高线图
根据粗略筛选结果缩小筛选范围至2-4~24,步长缩减至0.5进行精细筛选,筛选后的最终核函数参数g和惩罚参数c为16和0.5。精细筛选参数如图3所示。

图3 脱硝参数精细筛选等高线图
2 辅助变量选取
辅助变量的选取是运用支持向量机建立预测模型的主要步骤之一。由于辅助变量直接影响模型的准确度以及泛化性,所以在选取辅助变量时需要考虑多个因素,例如变量的类型、数目等,这些因素是密切相关的,但又相互制约。为了准确地选取辅助变量建立精确度更高的预测模型,本文采用皮尔逊相关系数与反应机理共同作用选取辅助变量。
2.1基于皮尔逊相关系数的辅助变量选取
从数据集中选取烟气量、烟气入口NOx浓度、烟气出口NOx浓度、烟气入口O2浓度、烟气出口O2浓度、接触时长、氨逃逸量和喷氨量8个变量作为待选变量。
皮尔逊相关系数又称皮尔逊积矩相关系数,它反映了2个定距变量间联系的紧密程度,用于度量2个变量之间的相关性(线性相关性),其值介于-1与1之间,一般用r表示,具体计算公式如下:
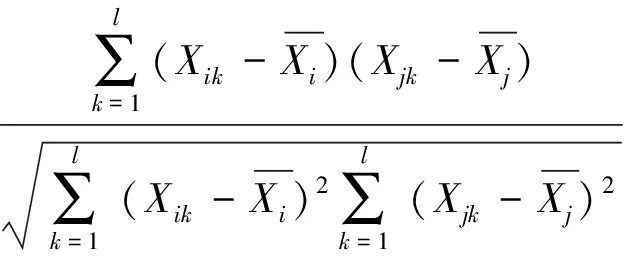
(6)
式中:Xi、Xj为定距变量;l为样本量。
利用SPSS数据分析平台计算8个待选变量与主导变量之间的皮尔逊相关系数。具体数据如表1所示。
皮尔逊相关系数r直接反映2个变量的相关性。当r>0时表示2个变量是正相关,即一个变量会随另一个变量的增大而增大;反之,当r<0时表示2个变量是负相关,即一个变量会随另一个变量的增大而减小。r的绝对值大小直接表明变量间相关性强弱。通常将0.8
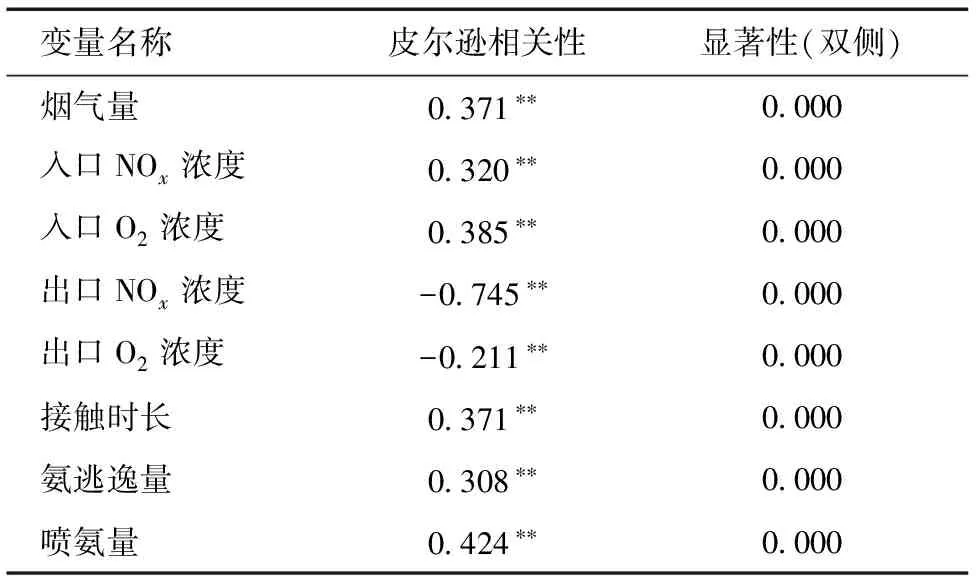
表1 脱硝系统皮尔逊相关系数表
注:**表示在0.01水平(双侧)上显著相关。
2.2基于反应机理的辅助变量选取
皮尔逊相关系数仅仅从变量间相关性出发选取辅助变量,存在一定的片面性,为了使预测模型的结果更精确,利用脱硝系统反应机理再次筛选待选变量。
(1)烟气量。在其他条件不变的情况下,脱硝效率与烟气量呈反比,即脱硝效率随着烟气量的减小而增加,这主要是因为烟气量增大会导致烟气流速增大,从而缩短烟气在催化剂模块的停留时间,反应物的接触时长会降低。
(2)烟气入口NOx浓度。在烟气量一定的情况下,烟气入口NOx浓度直接决定进入脱硝系统的NOx量。当喷氨量不变时,NOx量越大,烟气出口NOx浓度就越大,即系统脱硝效率的越小,反之亦然。
(3)接触时长。烟气在SCR反应器中与催化剂的接触时长是脱硝系统的一个关键的设计参数。接触时长增大有利于反应气体在催化剂微孔内的扩散、吸附、反应和产物气的解吸、扩散,从而提高脱硝效率,但若接触时间过长,会产生NH3的氧化反应,将会导致脱硝效率下降。
(4)氨逃逸量。氨逃逸量是衡量脱硝系统运行状态以及经济性的一个重要指标。脱硝效率随着氨逃逸量的增大而增大,最终稳定在一个数值[17]。
(5)喷氨量。在结构参数和其他运行参数不变的情况下,喷氨量与脱硝效率呈正比关系,喷氨量越大,脱硝效率越大,最终脱硝效率会趋于一个稳定的值。
(6)O2浓度。O2浓度会影响到NOx的生成,但是,在脱硝系统运行过程中,进出口O2浓度对脱硝效率影响较小,所以不能作为一个预测脱硝效率的辅助变量。
综上所述,通过皮尔逊相关系数与反应机理共同作用选取了烟气量、烟气入口NOx浓度、烟气出口NOx浓度、接触时长、氨逃逸量和喷氨量6个变量作为脱硝效率预测模型的辅助变量。
3 脱硝效率预测
脱硝效率预测模型的建立是在MATLAB平台下实现的。并利用某电厂脱硝系统实际运行数据对建立的模型进行验证。
3.1脱硝效率预测训练结果分析
随机选取50组脱硝系统实际运行数据作为模型的训练样本,通过训练模型训练样本,建立以辅助变量作为输入,脱硝效率为输出的预测模型。训练结果如图4所示。由图可见,训练样本的预测值与实际值变化趋势基本一致,每个点都高度吻合,个别点甚至完全重合。模型的相关系数为99.897 9%,均方误差MSE为6.574 68×10-5,说明模型具有较好的拟合特性。

图4 预测模型训练结果图
为了确定模型的精确度,将做出如图5所示的误差图。由图可得,误差分布在0值两侧,大部分样本点的误差集中在-0.2与0.2之间,最大绝对值小于0.25,说明预测模型具有较好的预测精度。
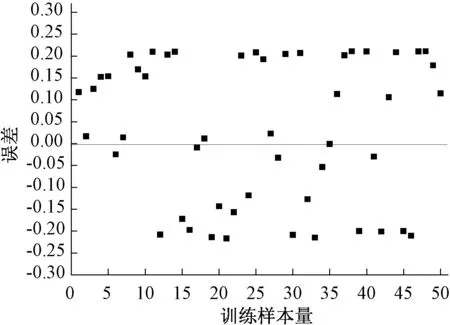
图5 预测模型训练误差分布图
3.2脱硝效率预测验证结果分析
上述分析说明预测模型具有良好的精确性,但不能确定模型的泛化性。为了证明模型的推广能力,从数据中再随机选取除训练样本外的20组脱硝系统实际运行数据对模型进行验证。验证结果如图6与图7所示。
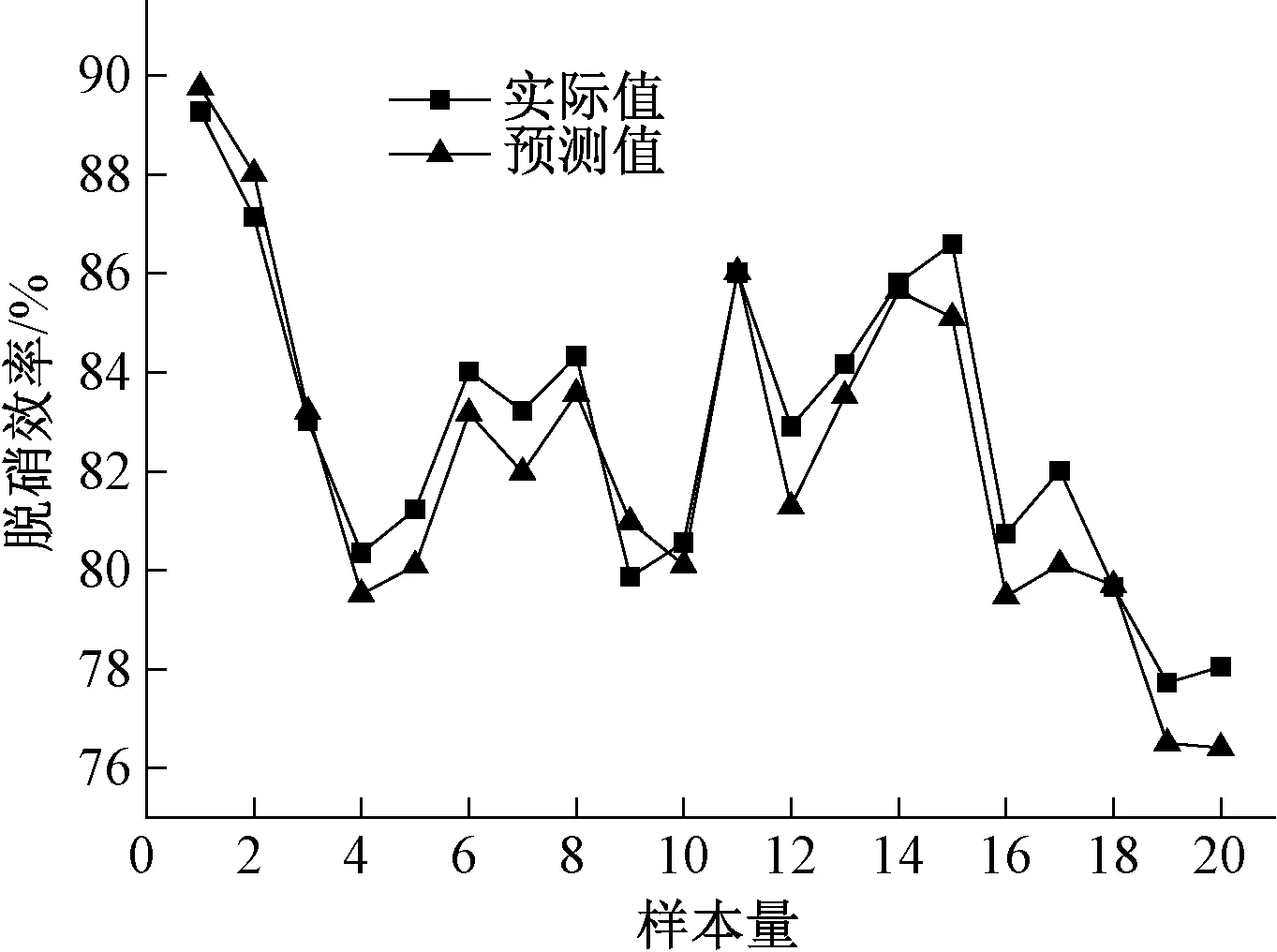
图6 预测模型验证结果图
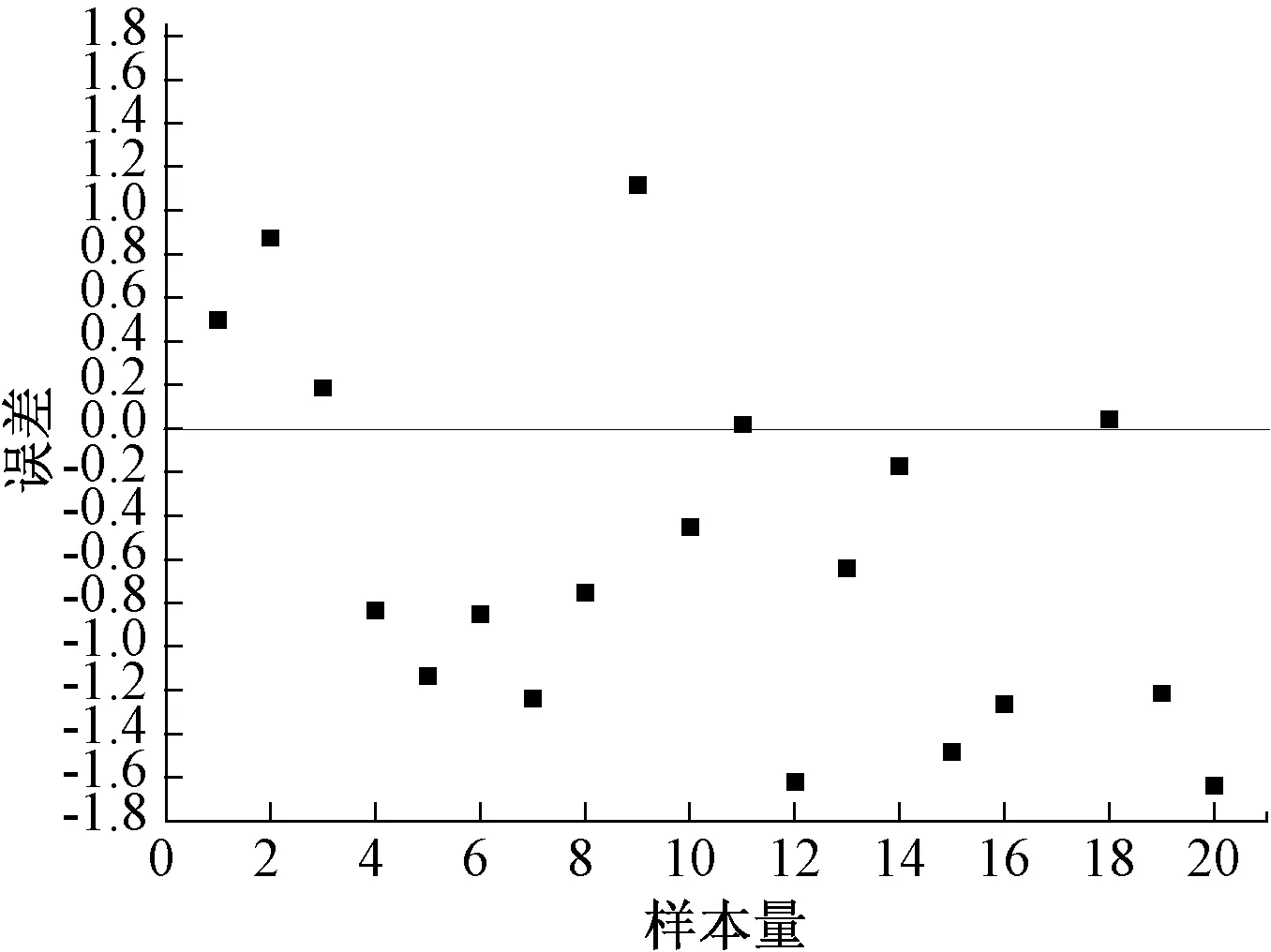
图7 预测模型验证误差分布图
由图6可见,图中2条曲线的走势一致,在各个折点均呈现较好的拟合特性,且在大部分样本点上出现高度重合现象。从图7可知,样本点的误差较多分布在0侧以下,说明预测值多数小于实际值,但误差最大绝对值小于1.8,个别样本的相对误差趋近0。综上可得该模型能精确地预测脱硝效率,且具有很好的推广能力。
4 结论
本文基于支持向量机算法建立了针对选择性催化脱硝效率的预测模型,并利用电厂脱硝系统实际运行数据对所建立的预测模型进行训练与验证。最终得出:
(1)利用皮尔逊相关系数与反应机理结合的方法选取的辅助变量可以很好地预测脱硝效率。
(2)通过采用交叉验证的方法对脱硝预测模型2个重要参数g和c进行粗略和精细2个步骤的选取,最终得到g和c分别为16和0.5。利用此方法可以提高脱硝预测模型的精确度。
(3)基于支持向量机算法建立的脱硝效率预测模型具有良好的拟合特性与泛化性,预测值与实际值变化趋势基本一致,相关系数可达99.897 9%;误差集中分布在-1.0~1.0之间,最大误差绝对值不超过1.8,能较好地满足工程实际需求。
[1] 中华人民共和国国家发展和改革委员会. “十三·五”规划纲要,2016.
[2] 郑海明,蔡小舒. 烟气连续排放监测系统计量相对准确度测试评估[J].计量学报,2007,28(1):85-88.
[3] 靳晓洁. TiO2光催化同时脱硫脱硝效率预测研究[D].保定:华北电力大学,2008.
[4] 归毅. 基于BP神经网络的SCR脱硝效率预测模型研究[D].保定:华北电力大学,2011.
[5] 赵毅,靳晓洁,赵莉,等. 预测TiO2光催化烟气同时脱硫脱硝效率的遗传程序设计方法研究[J]. 热力发电,2009,38(10):15-19.
[6] 秦天牧,刘吉臻,杨婷婷,等. 火电厂SCR烟气脱硝系统建模与运行优化仿真[J]. 中国电机工程学报,2016,36(10):2699-2703.
[7] 俞金寿.软测量技术及其应用[J].自动化仪表,2008,29(1):1-7.
[8] LI B, ZHENG D, SUN L, et al. Exploiting multi-scale support vector regression for image compr-ession[J].Neurocomputing,2007,70(4):849-858.
[9] CH S, ANAND N, PANIGRAHI B K. Streamflow forecasting by SVM with quantum behaved particle swarm optimization[J].Neurocomputing,2013,101(2):18-23.
[10] HONG W C. Traffic flow forecasting by seasonal SVR with chaotic simulated annealing algorithm[J].Neurocomputing,2011,74(2):2096-2107.
[11] 麻红波,余瑞锋,倪艳红,等.基于GSA-LSSVM的循环流化床锅炉飞灰含碳量预测[J].锅炉技术,2016,47(2):53-56,72.
[12] 尹凌霄,王明春,尚强. 基于支持向量机和粒子群算法的电站锅炉燃烧优化[J]. 锅炉技术,2014,45(2):13-17.
[13] 周尚珺玺,马立新.基于入侵杂草优化算法的支持向量机负荷预测[J]. 电力科学与工程,2017,33(2):35-40.
[14] 林德平.支持向量机在预测配煤灰熔点中的应用[J]. 电力科学与工程,2015,31(8):66-70.
[15] 李斌,邓煜,于文圣,等. 3种软测量技术在预测湿法烟气脱硫效率上应用的比较[J]. 汽轮机技 术,2016,58(3):226-230,234.
[16] VAPNIK V N.The nature of statistical learning theory[M].New York:Springer,1995:138-145.
[17] SI F, ROMERO C E, YAO Z, et al. Inferential sensor for on-line monitoring of ammonium bis-ulfate formation temperature in coal-fired powerplants[J].Fuel Processing Technology,2009,90(1):56-60.
Research on Prediction Model of Denitrification EfficiencyBased on Support Vector Machine
CUI Haibo1, YANG Haonan2, GENG Xiangjin1, LI Bin2, DENG Yu2
(1. Power Institute, Yunnan Electric Power Test&Research Institute(Group)Co. Ltd.,Kunming 650217,China; 2. School of Energy Power and Mechanical Engineering, North China Electric Power University, Baoding 071003, China)
The denitrification efficiency is influenced by many factors with strong correlation, which makes the denitrification efficiency difficult to measure in real time. In this paper, the auxiliary variables are selected by the combination of Pearson correlation coefficient and response mechanism, and the support vector machine is used to establish the prediction model with auxiliary variables as input and denitrification efficiency as output. And then the model is trained and verified based on the actual operation data of the denitrification system of a power plant. The results show that the correlation coefficient is 99.8979% and the mean square error is 6.57468 × 10-5. Most of the sample points have the errors between -1.0 and 1.0, and some errors tend to 0, and the maximum error is no more than 1.8. It shows that the prediction accuracy of the model is good and satisfactory, and it has good generalization ability and can meet the practical needs.
denitrification efficiency; Pearson correlation coefficient; response mechanism; support vector machine; prediction model
10.3969/j.ISSN.1672-0792.2017.10.006
X773
A
1672-0792(2017)10-0034-06
2017-07-24。
国家自然科学基金(51606066)。
崔海波(1979-),男,工程硕士,主要从事脱硫脱硝系统运行优化等方面的研究工作。
