基于经验模式分解的神经网络组合风速预测研究

勾海芝， 赵 征， 夏子涵

(华北电力大学 控制与计算机工程学院，河北 保定 071003)

基于经验模式分解的神经网络组合风速预测研究

勾海芝， 赵 征， 夏子涵

(华北电力大学 控制与计算机工程学院，河北 保定 071003)

为了提高风电并入电网的安全性，需要对风功率进行提前预测。风速预测是风功率预测的关键，而风速的不稳定性是预测的难点。为了降低风速的不稳定性，提高预测精度，提出经验模式分解法将风速分解并重组成2组不同的序列，对高频分量采用神经网络组合预测，剩余分量采取BP神经网络预测，并对两分量预测结果等权相加得预测结果。针对不同的样本进行建模预测，验证了该方法的适用性。并比较了GRNN、BP、LS-SVM 3种方法不同组合方式的预测精度，证明了在该组合方法中3种方法优势互补。

风速； 经验模式分解； GRNN； BP； LS-SVM； 组合预测

0 引言

近几年，环境污染、能源危机以及全球变暖等诸多问题日益严峻，新能源的开发利用迫在眉睫。我国将大力发展风电作为新能源战略的重点。风能的不稳定性和随机性会对电网的安全产生不利的影响。对风能进行有效地预测是减小风能对电网的冲击，提高风电在电力市场所占份额的有效途径。风速预测是风能预测的前提和基础，高精度的风速预测为风能预测提供了保障。

风速预测方法可以分为物理方法、统计方法。物理方法实质是利用气压气温等关键气象数据以及地表因素建立模型，获取某一点的风速预测值。统计方法是通过历史风速和风电场风速来建立模型，描述输入输出之间的映射关系，预测风速值。常用的统计方法包括神经网络法[1]、灰色预测法[2]、支持向量机法[3]等。在实际中常采用物理方法与统计方法相结合来达到较高精度的预测。文献[1]针对印度西部地区的多山区域，结合温度、气压、太阳辐射、海拔高度等因素建立神经网络模型预测每日的平均风速，预测结果的平均绝对百分比误差达到4.55%。文献[4]结合风机地理位置的相关性，引入了基于相关系数的回归分析方法，提高了风速的预测精度。在国内，大多数的研究集中在对统计方法的改进、优化、组合。文献[5]研究组合预测，发现组合预测精度高于任何一种单一预测精度，但是这种高精度的预测受单一模型预测误差之间关系的影响。文献[6]采用遗传算法优化BP神经网络的权值和阈值，提高了风速预测精度，改善了网络性能。除了优化算法本身，针对风速本身的特性，结合了一些先进算法从而提高预测精度。文献[7-8]针对风速序列的不平稳性，分别采用小波分解、经验模式分解法将风速序列分解为一系列简单的序列，并对这些序列一一预测，降低了序列不稳定性对预测精度的影响。

风速的不稳定性使预测的难度增加。针对此本文提出采用经验模式分解法将风速分为若干分量，并按照分量的特点重组成2组时间序列。针对其中最高频分量采用神经网络组合预测，另一分量采用BP神经网络预测，并比较对高频分量不同组合方法的精度，从而确定采用GRNN，BP，LS-SVM 3种方法的组合预测提高了预测精度。除此之外采用不同风速样本验证该方法的有效性以及适用性。

1 经验模式分解法

1.1经验模式分解

经验模态分解(EMD Empirical Mode Decomposition)算法是Hilbert-Huang变换(HHT)的核心算法。EMD算法的目的在于将性能不好的信号分解为一组性能较好的本征模函数(Intrinsic Mode Function，IMF)，其结果是将信号中不同尺度的波动或趋势逐级分解开来[9]。相对于小波分解法该方法更加简单，不需设定任意基函数。本征模函数需要满足以下2个条件：

条件1 信号的极值点数目和过零点数目的差值最多为1[10]；

条件2 由局部极大值和局部极小值构成的上包络线和下包络线的平均值为零。

EMD算法的计算步骤如下[11]：

(1)分析时间序列的变化趋势，找出序列x(t)的局部极大值点和极小值点。

(2)步骤(1)已经确定了局部极值点，采用3次样条函数把上述所有局部极大值点连接起来形成上包络线emax1(t)，而所有极小值点形成下包络线emin1(t)。应当注意的是，所有的数据点在上包络线和下包络线中间。

(3)确定均值包络线。将每一组局部极大值点和局部极小值点取平均值，将这些均值连接起来形成均值包络线。即均值包络线在上下包络线的中部。记为m1(t)。

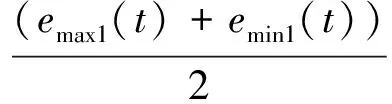
(1)

(4)计算原始序列x(t)与均值m1(t)的差值，记为

d1(t)=x(t)-m1(t)

(2)

(5)如果d1(t)符合上述IMF的2个条件，将d1(t)作为第1个被分解出的IMF分量：若不符合，将d1(t)作为原始待分解的时间序列。在此基础上继续重复执行步骤(1)～(4)，假设重复循环k次，得到d1k(t)=d1(k-1)(t)-m1k(t)满足上述IMF的条件。记c1(t)=d1k(t)，则c1(t)为x(t)经EMD分解后的第1个IMF，即IMF1。

(6)将分量c1(t)从原始时间序列x(t)中分离出来，将剩余分量r1(t)=x(t)-c1(t)当作新的原始待分解序列。继续重复执行步骤(1)～(5)，得到m个IMF，如果剩余项r(t)变成一不再发生变化的常数或单调变化的函数，则EMD分解过程结束。

经上述过程显示，原始序列x(t)可表示为m个IMF和最终余项的和。

(3)

式中：ci(t)为第i个IMF分量，代表了第i个被分离出来的信号分量，这些信号的特征尺度不同；r(t)为反映原始信号变化趋势的剩余分量项。

1.2经验模式分解法对数据处理

取部分样本数据对数据进行EMD分解，分解结果如图1所示。图中，signal对应原始信号x(t)，IMF1～IMF9分别对应公式(3)中的c1(t)～c9(t)，res对应r(t)。相对于其他分量，IMF1分量的规律性要差，反映了风速的高频不稳定部分。

图1 EMD分解图

将图1中最高频分量IMF1叫做分量2，剩余其他分量即IMF2-IMF9，res重组为一个分量叫做分量1。运用BP神经网络分别对两分量建模，神经网络实际网络输出与目标输出的回归曲线如图2，3所示。

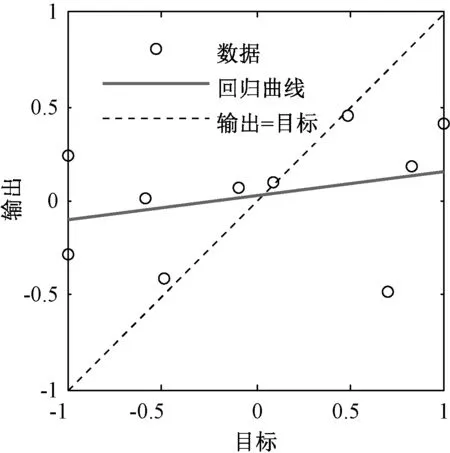
图2 BP神经网络对分量2的回归曲线

在图2中，对于分量2，BP神经网络的拟合效果很差，网络输出与目标输出的相关系数小于0.4，回归曲线斜率0.13，说明了仅使用BP神经网络法对分量2不能得到很好的预测效果；在图3中，分量1的神经网络输出与目标输出相关系数大于0.96，回归曲线的斜率是0.98，表明分量1仅使用BP神经网络有较好拟合效果。这一拟合结果在一定程度上说明了，最高频分量的预测是风速预测准确性的关键环节，最高频分量的预测效果如果能够改善，预测精度就能够有所提高。

2 基于经验模式分解的神经网络组合预测模型

2.1BP网络

BP神经网络是目前应用最广泛的神经网络模型之一。BP神经网络应用梯度下降法通过信号正向传播和误差反向传播不断地修正网络权值和阈值从而使网络的输出值与期望值均方差最小，即输出值无限的接近期望值[6]。

2.2GRNN网络

广义回归神经网络[8](GRNN)是一种径向基神经网络，对于非线性系统的映射能力很强，学习速度较快，相对于传统的RBF具有很明显的优势。当数据较少时，预测效果相对较好。除此之外，在不平稳数据的处理上，GRNN网络也表现出了较大优势。

2.3最小二乘支持向量机

支持向量机需要的数据少，训练速度快，对于解决非线性问题有很大的优势，其中的最小二乘支持向量机[3]将传统支持向量机的不等式约束条件转变为等式约束条件，这样二次规划问题的求解就被转化为线性方程组的求解问题。在这个过程中，计算过程被简化，加快了计算速度，同时预测精度也得到了一定提高。其目标函数为

(4)

约束条件为

yi=ωT.φ(xi)+b+ξi,i=1,…,m

(5)

式中：c是惩罚参数；ξi为误差向量；ω表示权重向量；b表示偏差；φ(xi)表示原始变量数据映射之后的值。根据公式(4)和(5)建立的拉格朗日函数公式为：

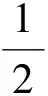
(6)

利用最小二乘法，得回归预测函数为

(7)

式中：αi为拉格朗日算子；K(x,xi)=〈φ(x),φ(xi)〉为核函数。

2.4基于经验模式分解的神经网络组合预测

基于经验模式分解的神经网络组合算法的流程图如图4所示。

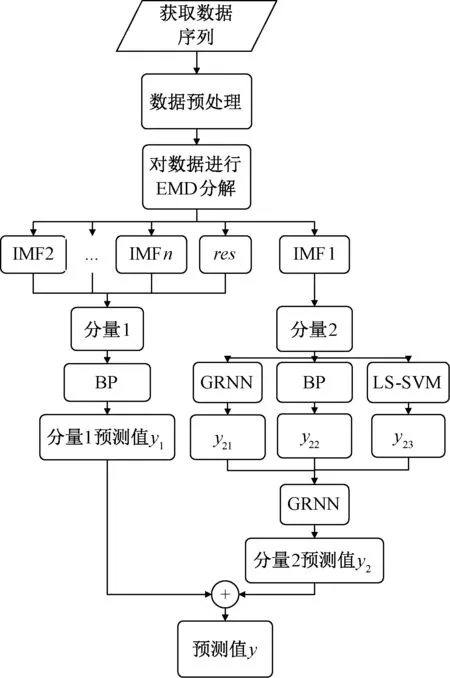
图4 算法流程图

基于经验模式分解的神经网络组合算法将风速样本数据经过经验模式分解得到m个IMF分量和一个剩余分量res。由于IMF1分量随机性要强，规律性差，所以将其他分量IMF1分量与其他分量分割开来，其他分量的和被称为分量1，IMF1分量被称为分量2。对分量1建立BP网络模型进行预测，得出预测结果y1。对分量2分别采用GRNN、BP、LS-SVM、预测得出预测结果y21、y22、y23，并将三预测结果建立GRNN模型进行组合预测，得出分量2的最后预测值y2。y1、y2等权相加得出最后风速预测值y。

3 实例

3.1数据描述

分别采用两电厂8～9月份每小时平均风速数据作为样本数据，如图5所示。其中样本1平均风速为2.28 m/s，风速平均变化量为1.11 m/s，风速变化范围为0～12 m/s，样本2平均风速为6.24 m/s，风速平均变化量为0.73 m/s,风速变化范围为1.5～16 m/s。从数据分析可以看出样本1平均风速低，但是风速更加不平稳；样本2平均风速高，风速变化平稳。

图5 样本风速数据

针对2个不同样本，根据2.4节所述采用经验模式分解法对数据进行分解，并重组为分量1和分量2，对分量1采用BP网络预测，对分量2分别采用BP，GRNN，LS-SVM进行预测，并将预测结果采用GRNN网络组合预测。除此之外，将上述3种方法分别两两组合预测分量2，比较最终风速预测结果。

3.2结果及分析

两风速样本基于EMD的神经网络组合风速预测效果和传统神经网络风速预测结果图如图6、7所示。在图中，无论对于风速样本1还是样本2，本文提出的方法预测结果均能较好的跟踪风速变化。在图6中，对于数据样本1，风速变化范围大，变化快，在风速较低的第1～11点，取得了很好地预测效果，在19～20点，虽然风速变化快，预测风速与实际风速差别较小，其他的风速点预测效果欠佳；在图7中，对于数据样本2，风速变化范围小，风速预测效果几乎与风速变化同步，改善了传统神经网络预测的滞后性，在变化突兀的时间点1～10，出现了相对较大的偏差。

图6 样本1风速预测结果

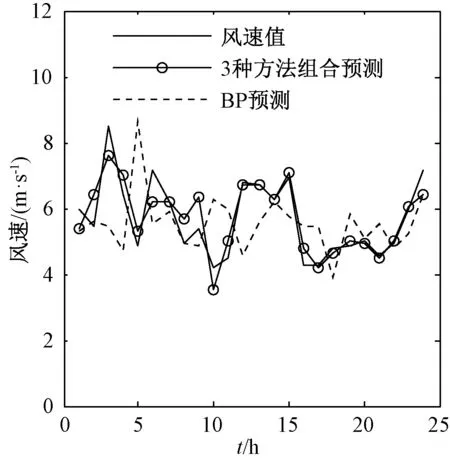
图7 样本2风速预测结果

在预测结果误差图8和图9中，采用GRNN，BP，LS-SVM 3种方法对分量2组合预测与采用任意两种方法的组合预测相比，预测优势不是很明显，但是在变化较大的点，预测精度得到了改善，预测误差得到降低。因此证明了在此类预测方法中，3种方法对于提高风速的预测精度均发挥了一定的作用。并且对于样本1，3种方法组合优势明显。

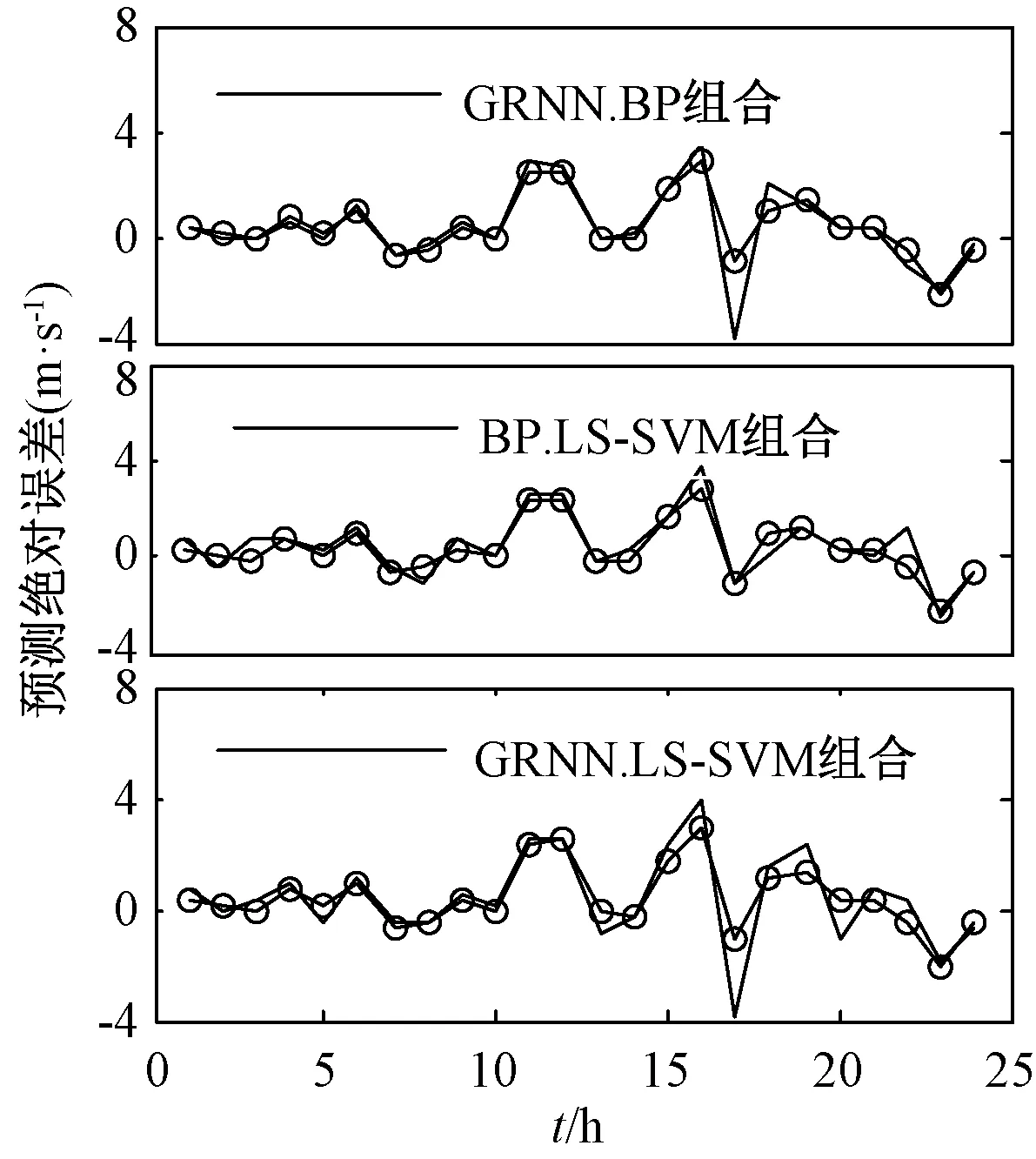
图8 样本1预测绝对误差

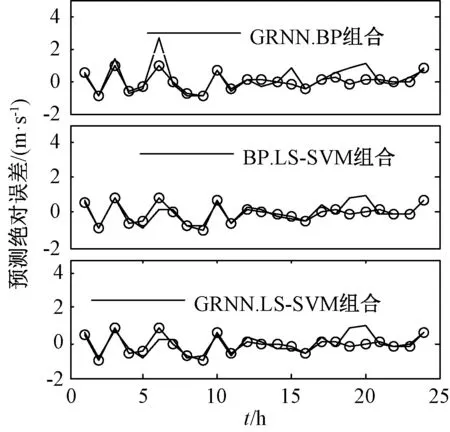
图9 样本2预测绝对误差

为了比较各种预测方法的精度采用平均绝对百分比误差和均方根误差作为评价标准[8]。平均相对误差绝对值为

(8)

均方根误差为

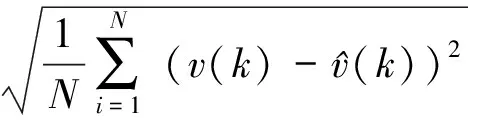
(9)

由表1数据可以看出，采用经验模式分解法的预测精度均高于原BP神经网络。对于样本1和样本2，预测精度均得到较大程度地提高，说明本文提出方法对于稳定性不同的的序列均能改善其预测精度。对于数据样本1，风速平均变化量较大，不稳定性强，仍取得了较好的预测效果，表明文中预测方法对于降低序列的不平稳性有很强的优势。从表中数据仍能明显的看出，对变量2采用3种方法组合预测效果要优于任何一种方法单独预测，以及任一两种方法组合预测，表明了3种方法结合了每一种方法的优势，达到了提升预测精度的目的。

表1 不同方法预测结果表

注：①②③分别为GRNN，BP，LS-SVM方法。

4 结论

风速不稳定性会降低风速预测的精度。经验模式分解法对于处理不平稳序列有很强的优势。本文应用经验模式分解法处理风速时间序列，根据分解序列的特点将序列分解成分量1和分量2，对分量1采用BP网络预测，对分量2采用BP、GRNN、LS-SVM 3种方法组合预测。预测结果显示，此类组合方式有效的结合每一种预测方法的优点，改善了原有神经网络预测的滞后性，降低了风速不平稳性对风速预测效果的影响,提高了预测精度。

[1] RAMASAMY P， CHANDEL S S，YADAV A K．Wind speed prediction in the mountainous region of India using an artificial neural network model[J]．Renewable Energy，2015，80(8):338-347.

[2] 李颖男，赵征.基于灰色理论的风电功率预测研究[J].电力科学与工程，2016，32(8):32-36.

[3] 周腊吾，陈静，戴浪.基于最小二乘支持向量机的风速组合预测模型[J].科技导报，2011，29(7):66-68.

[4] 王印松，苏子卿.一种基于相邻风机测量数据相关性分析的风速预测方法[J].华北电力大学学报(自然科学版)，2015，42(2):91-96.

[5] 彭怀午，刘方锐，杨晓峰.基于组合预测方法的风电场短期风速预测[J].太阳能学报，2011，32(4)：543-547.

[6] 王德明，王莉，张广明.基于遗传BP神经网络的短期风速预测模型[J].浙江大学学报(工学版)，2012，46(5):837-841，904.

[7] 高阳，钟宏宇，陈鑫宇，等.基于神经网络和小波分析的超短期风速预测[J].可再生能源，2016，34(5):705-711.

[8] 王韶，杨江平，李逢兵，等.基于经验模式分解和神经网络的短期风速组合预测[J].电力系统保护与控制，2012，40(10):6-11，18.

[9] SHENGWEI F.A hybrid model of EMD and multiple-kernel RVR algorithm for wind speed prediction[J].International Journal of Electrical Power & Energy Systems，2016，78(6):910-915.

[10] WANG S X， ZHANG N， WU L， et al.Wind speed forecasting based on the hybrid ensemble empirical mode decomposition and GA-BP neural network method[J].Renewable Energy，2016，94(8):629-636.

[11] 刘辉，张雷，田红旗，等.基于经验模式分解和自适应神经模糊推理的风速短期智能预测混合方法[J].中南大学学报(自然科学版)，2016，47(2):676-682.

Research on Neural Network Combined Wind Speed Prediction Based on Empirical Mode Decomposition

GOU Haizhi， ZHAO Zheng， XIA Zihan

(School of Control and Computer Engineering, North China Electric Power University, Baoding 071003，China)

In order to improve the safety of the wind power integrating into the power grid, it is necessary to predict the wind power ahead of time. The wind speed prediction is the key to wind power prediction, and the instability of wind speed becomes the conundrum for the prediction. In order to reduce the instability of wind speed and improve prediction accuracy, an empirical mode decomposition method is proposed to decompose the wind speed into two groups of different sequences, and the high frequency components are predicted by neural network combination while the residual components are predicted by BP neural network. The prediction results are obtained by adding the two components calculated by the above two networks respectively. The applicability of the method is verified by modelling different samples. And three different methods, GRNN, BP, and LS-SVM, are combined in different ways to conduct the prediction, and the accuracies are compared. The results show that they have their own advantages with different combinations, which confirms that these three methods could complement each other.

wind speed; empirical mode decomposition; GRNN; BP; LS-SVM; combimation prediction

10.3969/j.ISSN.1672-0792.2017.10.011

TM614

A

1672-0792(2017)10-0062-06

2017-06-29。

新能源电力系统国家重点实验室开放课题(LAPS16008)。

勾海芝(1991-)，女，硕士研究生，研究方向为风速预测及风功率预测研究。