双曲正切跟踪微分器设计及相平面分析
2017-11-09刘延泉郭佳颖
刘延泉, 郭佳颖
(华北电力大学 控制与计算机工程学院,河北 保定 071003)
双曲正切跟踪微分器设计及相平面分析
刘延泉, 郭佳颖
(华北电力大学 控制与计算机工程学院,河北 保定 071003)
针对离散跟踪微分器(Han-TD)加速度函数结构复杂、参数整定繁琐的不足,提出了双曲正切函数改进微分器的加速度函数。双曲正切函数是一种光滑连续非线性函数,该函数在坐标零点附近呈线性特性,所以消除震颤效果显著。通过使用李雅普诺夫第二定理从理论证明了改进跟踪微分器的全局收敛的稳定特性。使用相平面法寻找微分器奇点的稳定结点,进一步指导参数的整定。通过MATLAB仿真,比较双曲正切跟踪微分器(Tanh-TD)与Han-TD的跟踪微分性能和滤波特性。仿真结果表明,双曲正切跟踪微分器对输入信号的跟踪可以实现快速无超调,滤波性能更优,且提取的微分信号较为理想,具有工程实用价值。
双曲正切函数; 跟踪微分器; 李雅普诺夫第二定理; 相平面
0 引言
跟踪微分器(TD)最早由韩京清等研究学者于1994年提出,实现了从含有噪声的测量信号以及不连续信号中提取出连续滤波信号和微分信号的功能[1]。由于跟踪微分器具备良好的信号滤波和求导特性,其在电动机控制[2]、机器人[3]、飞行器[4]等控制系统中有广泛的应用。针对跟踪微分器系统,许多学者对其加速度函数进行了分析研究,并给出了改进方案。文献[5]通过对滑模算法的分析,提出了将滑模技术应用于微分器中,但由于该控制器中存在切换函数,系统易出现抖振问题且参数不易整定。文献[6]针对离散跟踪微分器和快速型跟踪微分器的研究,提出了将非线性的幂指函数应用于微分器,改进后的微分器具有较好滤波特性以及良好的动态响应,但加速度函数过于复杂。文献[7]提出高增益微分器,能够准确求取时间导数,但对高频噪声不敏感且易出现峰值现象。
本文将使用具有光滑非线性特性的双曲正切函数改进跟踪微分器的加速度,改进后的控制器不但跟踪速度较快,而且没有超调现象,对输入信号实现良好的滤波和微分效果。
1 跟踪微分器设计
设计跟踪微分器的核心为加速度函数,加速度函数的选取决定了跟踪微分器的性能好坏。目前,跟踪微分器主要从线性加速度跟踪微分器和非线性加速度跟踪微分器2类进行分析研究[8]。在零点附近,函数具有线性特性可获得良好的稳态性能;在远离零点时,函数具有符号函数特性可具备良好的动态性能。设计新的跟踪微分器可以从函数特性角度去构造选取。
1.1双曲正切加速度函数
双曲正切加速度函数f(x)=tanh(x)定义如下:

(1)
定义域区间(-∞,+∞);

(2)
由式(1)和式(2)可推,双曲正切函数是奇函数。
(3)
由上式(3)可知,f′(x)的值永远大于等于1,所以f(x)单调递增。

(4)
双曲正切函数及其导数图像如图1所示。

图1 双曲正切函数及其导数曲线
从图1曲线以及导数极限(4)可知,在原点附近,双曲正切函数呈线性特性,在X趋于无穷大,函数f(x)为饱和函数,即双曲正切是一个非线性光滑函数[9]。
1.2微分器结构及稳定性分析
双曲正切跟踪微分器结构如式(5)所示:
(5)
式中:v(t)为系统的输入信号;x1(t)为系统跟踪信号;x2(t)为系统跟踪微分信号;R,a1,a2,b1,b2为系统调节参数。
定理1:对于系统
(6)
如果a1,a2,b1,b2均为正数,则系统在原点(0,0)呈全局一致渐进稳定特性。
证明:选取(0,0)领域内的Lyapunov函数
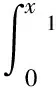
(7)
由于a1,b1为正数,当x1≠0时,x1与tanh(b1x1)符号相同,所以x1·(a1(tanh(b1x1)))>0,即
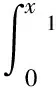
(8)
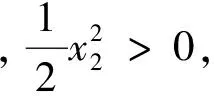
对v(x1,x2)的时间t求导可得:

(9)

(10)

定理2:对于系统
(11)
如果a1,a2,b1,b2均为正数,x1(t)→0,x2(t)→0 (t→∞),则对任意有届可积函数v(t)和任意常数T>0,式(11)的解x1(t)满足:
(12)
定理2该定理从理论上阐明了系统在任意时间常数T内,当R趋于无穷大时,系统跟踪信号x1(t)无限接近系统的输入信号v(t)。
2 相平面分析
相平面分析法不仅能够自动精确地绘制控制系统的相平面图,还能够快速地分析系统各个参数对控制系统的影响,从而研究出系统参数整定规律。本文主要使用相平面法来寻找微分器奇点的稳定结点,指导系统参数的整定。
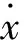
(13)
x1=x2=0,所以φ(x1,x2)=0

(14)

因此,可将系统(11)近似为线性系统:
(15)
式(15)的系数矩阵:
该特征值
(16)
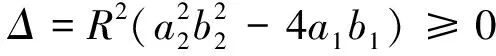
如图2所示,当X取不同值时,该微分器系统的相轨迹总是沿着同样的2个方向平行趋于奇点(0,0)。从图中还可得出,当奇点为稳定结点类型时,系统是直接收敛,且跟踪微分器系统处于过度过程产生的振荡比较小。

图2 稳定结点相轨迹图
3 系统参数整定
从式(5)可知,系统需要整定的参数有R,a1,a2,b1,b2。R值越大,系统的跟踪速度越快,但是信号微分效果会变差,即降低了系统的滤波特性。a1和b1参数对系统的跟踪速度影响作用相似,当a1或b1增大,系统的跟踪速度将变快,同时降低了系统的滤波性能。a2和b2参数对系统的微分效果影响相似。当a2或b2增大,系统的跟踪速度会降低,但提升了系统的滤波特性。因此,可以先设定b1,b2的值,再设定R值调节微分器的跟踪效果,最后通过调节a1,a2的值来平衡系统跟踪和微分的整体效果。
4 仿真结果及分析
为了验证双曲正切跟踪微分器的改进效果,使用MATLAB工具进行仿真,将改进的跟踪微分器和文献[10]提出的快速离散跟踪微分器进行比较,从而分析系统的控制效果。
4.1跟踪和微分性能
系统输入信号选取幅值为1的方波信号。当比较系统的跟踪性能时,仿真中双曲正切跟踪微分器的参数为:R=10,a1=4,a2=4,b1=1,b2=1快速离散跟踪微分器的参数为:R=50,h=0.01。当比较系统的微分性能时,快速离散跟踪微分器R值改为100。微分性能相似比较跟踪信号曲线如图3所示,跟踪性能相似比较微分信号曲线如图4所示。
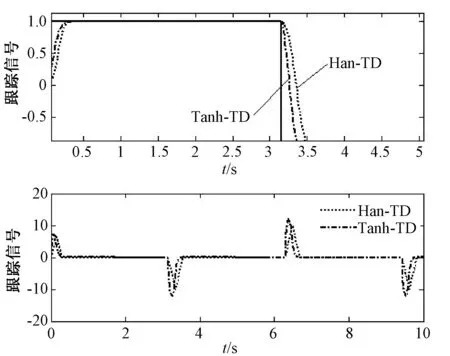
图3 微分性能相似比较跟踪信号曲线
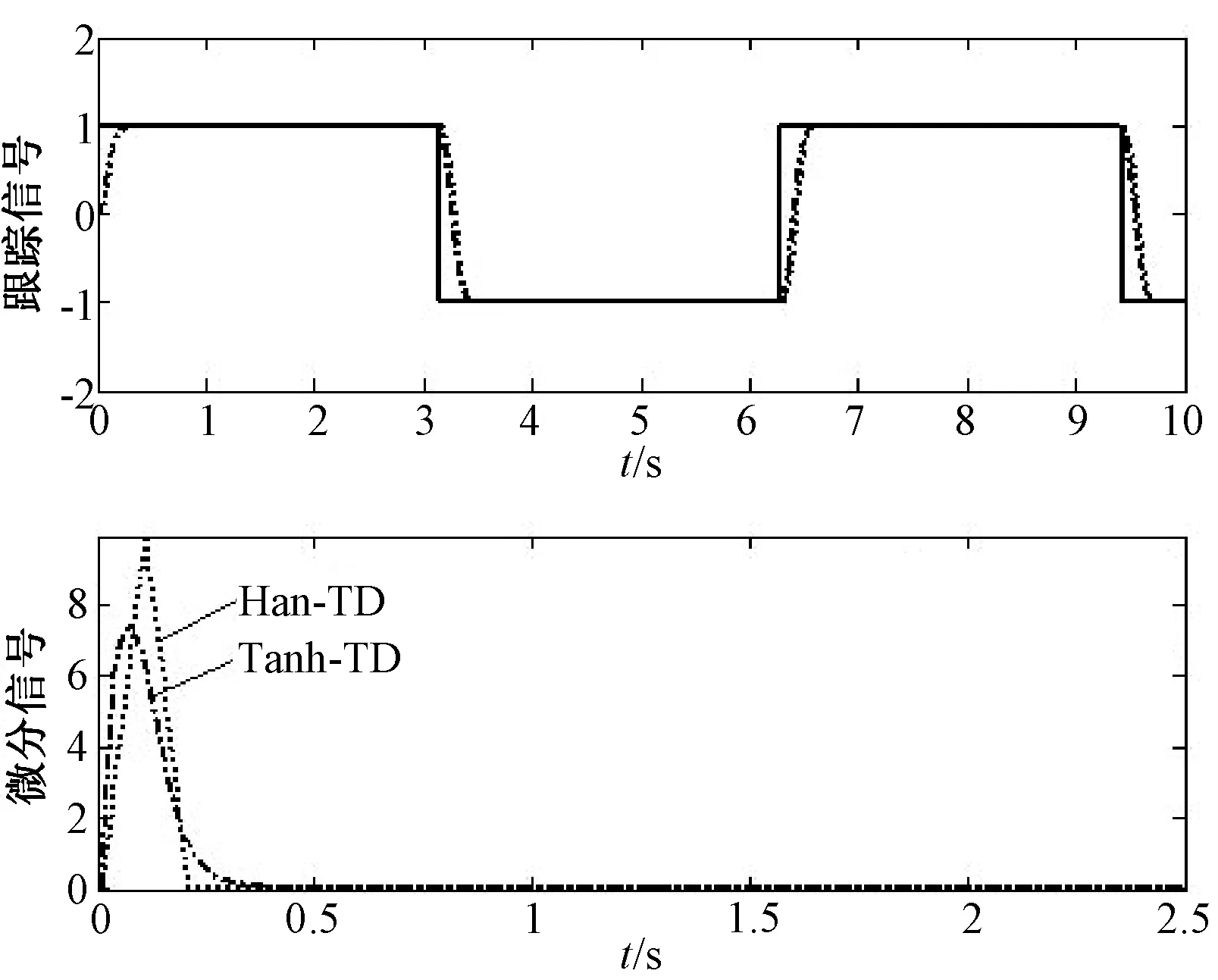
图4 跟踪性能相似比较微分信号曲线
从图3可以看出,当系统微分性能比较相似的时候(指此时达到相同峰值),2种跟踪微分器都能较快地跟踪输入的方波信号,但双曲正切跟踪微分器的响应速度优于快速离散跟踪微分器,即跟踪效果更优,且二者均无超调现象。从图4可以看出,当系统跟踪效果相似的时候(指此时跟踪曲线重合),双曲正切跟踪微分器的微分信号曲线峰值低于快速跟踪微分器,且双曲正切跟踪微分器输出的微分信号呈钟形曲线,Han-TD输出的微分信号呈三角形曲线,可见Tanh-TD的微分性能更好。
4.2滤波性能
在幅值为1的方波信号中加入方差为0.05的随机噪声信号,观察双曲正切跟踪微分器的滤波性能,滤波信号曲线如图5所示。

图5 滤波信号曲线
图5的上半幅为2种跟踪微分器对噪声污染的方波信号的跟踪曲线,其中,输入的噪声信号均值为0。从图中可以看出,双曲正切跟踪微分器能较好地从被噪声污染的方波信号中提取出原信号。图5的下半幅为2种跟踪微分器对噪声污染的方波信号的微分信号曲线,从图中可知,Han-TD对噪声微分作用比较强,Tanh-TD能较好地避免对噪声信号的放大作用。可见,相对于快速离散跟踪微分器(Han-TD),双曲正切跟踪微分器能更好地过滤噪声信号,输出的微分信号也相对较好,即Tanh-TD滤波性能较好。
5 结论
针对目前经常使用的快速离散跟踪微分器的不足,设计了双曲正切跟踪微分器,双曲正切加速度函数形式结构简单,调节参数方便,具备良好的稳态性能和动态性能。通过理论证明了改进的跟踪微分器拥有全局收敛的稳定特性,通过参数调整保障了系统奇点类型为稳定结点。仿真结果表明,双曲正切跟踪微分器比快速离散跟踪微分器具有更强的跟踪性能和微分效果以及更好的滤波特性,具有工程实用价值。
[1] 李杰,齐晓慧,万慧,等. 自抗扰控制:研究成果总结与展望[J]. 控制理论与应用, 2017,34(3):281-294.
[2] 左月飞,刘闯,张捷,等. 永磁同步电动机转速伺服系统PI控制器的一种新设计方法[J].电工技术学报,2016,31(13):180-188.
[3] 李殿起,段用. 用跟踪微分器实现机器人自抗扰控制[J].兵工学报,2016,37(9):1721-1729.
[4] 庄超玮,蒋炳炎,赵党军,等.基于跟踪微分器的四旋翼飞行器控制器[J].计算机仿真,2015,32(5):114-118.
[5] 姚刚.机电系统加速度估计方法与应用[D].哈尔滨:哈尔滨理工大学,2015.
[6] 史永丽,候朝桢.改进的非线性跟踪微分器设计[J].控制与决策,2008,23(6):647-650.
[7] AHRENS J H, KHALIL H K.High-gain observers in the presence of measurement noise:A switched-gain approach[J].Automatica,2009,45(4):936-943.
[8] 王新华,刘金琨.微分器设计与应用-信号滤波与求导[M].北京:电子工业出社,2010:96-106.
[9] 于伟锋,陈鸿伟.基于试验和BP神经网络的CFB锅炉脱硫效率研究[J].电力科学与工程,2013,29(8):50-56.
[10] 韩京清.自抗扰控制技术-估计补偿不确定因素的控制技术[M].北京:国防工业出版社,2008:66-72.
Design and Phase Plane Analysis of a Hyperbolic Tangent Tracking Differentiator
LIU Yanquan, GUO Jiaying
(School of Control and Computer Engineering, North China Electric Power University, Baoding 071003, China)
According to the deficiencies of the discrete tracking differentiator (Han-TD) acceleration function, such as complex structure and parameter setting, an acceleration function of a hyperbolic tangent function improvement differentiator is proposed. The hyperbolic tangent function is a smooth continuous nonlinear function, which is linear in the vicinity of coordinates 0, so the effect of eliminating the tremor is remarkable. By using Lyapunov’s second theorem, the stability of the global convergence of the improved tracking differentiator is proved theoretically. The stability node of the singularity of the differential device is found by using phase plane method, and the parameter tuning is further guided. The tracking differential performance and filtering characteristics obtained by hyperbolic tangent tracking differentiator (Tanh-TD) and Han-TD respectively are compared by MATLB simulation. The simulation results show that the hyperbolic tangent tracking differentiator can realize the fast non-overshoot with better filtering performance, and the differential signal of extracting is ideal, which has the practical value for engineering.
hyperbolic tangent function; tracking differentiator; Lyapunov’s second theorem; phase plane
10.3969/j.ISSN.1672-0792.2017.10.013
TM273
A
1672-0792(2017)10-0074-05
2017-05-02。
刘延泉(1963-),男,副教授,主要研究方向为PLC、DCS及其应用、协调控制系统优化等方面。郭佳颖(1992-),女,硕士研究生,主要研究方向为先进控制理论及其在电力系统中的应用。
