基于雷达测量的炮位和落点快速预测方法研究*

陈健伟,王良明,李子杰

(南京理工大学能源与动力工程学院,南京 210094)

基于雷达测量的炮位和落点快速预测方法研究*

陈健伟,王良明,李子杰

(南京理工大学能源与动力工程学院,南京 210094)

针对利用雷达测量数据进行炮位和落点预测时“先跟踪,后预测”缺乏快速性的问题,提出一种以雷达采样点数为分段参量将抛物线近似、最小二乘拟合、非线性滤波等算法进行综合的炮位预测分段算法和落点预测加权算法。以某120 mm迫弹为例进行仿真,结果表明,炮位预测分段算法能够在雷达获取两组测量数据时开始预测;落点预测加权算法在雷达获取首个测量数据时即进行预测,且在雷达采样数据较少时具有比非线性滤波算法更高的落点预测精度。

雷达数据处理;非线性滤波;炮位预测;落点预测

0 引言

炮位侦校雷达的主要功能有两个:一是通过搜索跟踪敌方弹丸并推算出发射该弹丸的火力装备的位置坐标;二是通过跟踪己方弹丸获取量测数据并预测弹丸落点坐标,供己方进行射击校正。由于其具有探测距离远、反应速度快、机动性能强的优点,在现代化战争中发挥着越来越重要的作用[1]。

目前国内外利用量测数据进行弹道预测的方法主要有两种;一是基于先验样本的机器学习算法,由于炮位侦校雷达对弹道辨识的实时性要求较高,且难以提供机器学习所需的大量准确的先验样本,因此该算法不适用于炮位侦校雷达数据处理;二是应用较为广泛的基于弹道模型的卡尔曼滤波估计算法。文献[2]则利用了无迹卡尔曼滤波算法对测量数据进行处理并进行弹道预测,同时对EKF和UKF两种算法进行了分析比较;文献[3]在传统扩展卡尔曼滤波基础上引入渐消因子,形成渐消记忆卡尔曼滤波,使得滤波精度和收敛性有了一定提高;文献[4]采用粒子滤波算法对弹道下降段进行跟踪并外推炮位,获得了比扩展卡尔曼滤波更高的精度。

采用卡尔曼滤波算法进行弹道预测的前提是必须能够获取足够的量测数据,而在工程实践中,雷达所能获取的数据量往往受到各种条件的限制,当雷达量测数据较少时,就会导致滤波精度严重下降,从而影响炮位或落点的预测。文中基于此,将分段理论与加权理论应用于炮位和落点预测,对多种外弹道数据处理方法进行综合,提高雷达采样数据较少时的弹道预测精度,使雷达能够实现“边跟踪,边预测”,提高其数据处理的快速性。

1 基于雷达数据的弹道滤波

1.1 非线性滤波算法

由外弹道理论[5]可知,炮弹的飞行轨迹为非线性过程,因此需采用非线性系统的滤波技术对炮位侦校雷达数据进行处理,目前应用较为广泛的有扩展卡尔曼滤波(EKF)算法和无迹卡尔曼滤波(UKF)算法[6]。

扩展卡尔曼滤波通过泰勒级数展开这一手段将非线性滤波问题转化为近似的线性滤波问题,利用线性滤波的相关理论来解决原非线性滤波问题的,为一种次优滤波算法。

基于无迹变换(UT)的UKF算法不需要对系统非线性状态和量测模型进行线性化,而是对系统状态向量概率密度函数(PDF)近似化,近似化之后的PDF仍然满足高斯分布,但其表现形式变为一系列选取好的采样点。EKF算法和UKF算法过程推导及变量定义详见文献[6,8]。

1.2 滤波模型

考虑到炮位侦校雷达数据处理的快速性要求,这里采用形式较为简单的质点弹道模型[7]进行滤波。

(1)

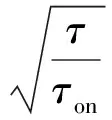
取状态变量为:

X=[x,y,z,vx,vy,vz,c]T=[x1,x2,x3,x4,x5,x6,x7]T

(2)

记量测变量为:Y=[rβε]T,根据地面坐标系与雷达天线坐标系的转换关系[7],建立如下量测方程:

(3)

式中：d为雷达量测噪声,在仿真研究中假设d为一零均值高斯白噪声,且有:d～N(0,R),其余滤波变量计算过程可参考文献[7]。

2 炮位快速预测方法

兼顾炮位侦校雷达实时性和准确性的工作要求,本节将外弹道数据处理中常用的几种方法进行综合,提出一种炮位快速预测算法。

2.1 抛物线近似法[9]

当雷达获得两组量测数据后,通过卡尔曼滤波技术无法获得准确的弹道参数来进行弹道解算。若忽略空气阻力,可以用弹丸在真空中的飞行轨迹为一抛物线这一性质来进行粗略的弹道轨迹预测。

以时间t为参量的坐标形式的弹丸抛物线弹道方程:

x=v0cosθ0t

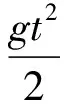
(4)

式中:v0为弹丸初速;θ0为射角;g为重力加速度。

如图1所示,在雷达天线直角坐标系下XOY平面内,炮位侦校雷达获取敌方来袭炮弹飞行过程中的两点数据P1(r1,β1,ε1)和P2(r2,β2,ε2),两点间的弹丸飞行时间为Δt,炮弹出炮口到飞行至P1的时间为T,两点的高度分别为:

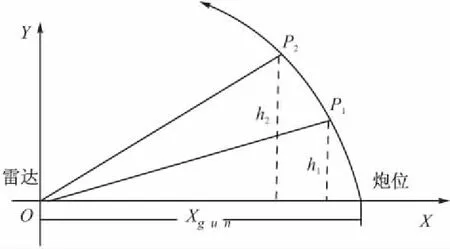
图1 XOY平面内抛物线弹道示意图

经计算推导可得地面坐标系下炮位距雷达站距离:

Xgun=r1cosβ1cosε1+T·(r1cosβ1cosε1-

r2cosβ2cosε2)/Δt

(5)

同理可得Zgun,并进而求得炮位坐标。

2.2 最小二乘拟合法

弹丸飞行弹道近似为一抛物线,因此,可将炮位侦校雷达获得的n个测量数据转换至雷达天线直角坐标系下,即(xi,yi,zi)(i=1,2,…,n),在雷达天线坐标系O1-XRYRZR内对数据点(yi,xi)和(yi,zi)分别进行最小二乘拟合,得到拟合函数后即可求出雷达天线坐标系下敌方炮位海拔hgun对应处的(xgun,zgun)。

2.3 分段预测算法

在雷达采样点数较少时,采用滤波算法进行炮位外推会产生较大误差,基于此,设计分段预测炮位方案,其流程如图2所示。

图2 分段炮位预测流程图

图2中,n为雷达采样点数,当雷达采样点达到2个时,即根据抛物线弹道外推炮位;当雷达采样数据为3个到5个时,采用最小二乘拟合的方法外推炮位;当雷达采样点数逐渐增多,达到5个以后时,则通过非线性滤波算法进行炮位预测。

3 落点快速预测算法

由于校射模式下已知我方发射弹丸的发射条件以及弹丸参数,因此可结合理论弹道对炮弹落点进行预测。

3.1 方案弹道结合测量数据的预测方法

当雷达获取第一个测量数据时,经坐标转换后可以根据该数据得到发射坐标系下包含噪声的弹丸位置信息(xm,ym,zm),无法得到弹丸飞行的速度信息。根据炮弹飞行的理论弹道,可以求得炮弹在该位置处的理论速度(vxl,vyl,vzl),以该点的理论速度作为落点预测的速度信息,结合理论弹道模型便可求出炮弹的落点。

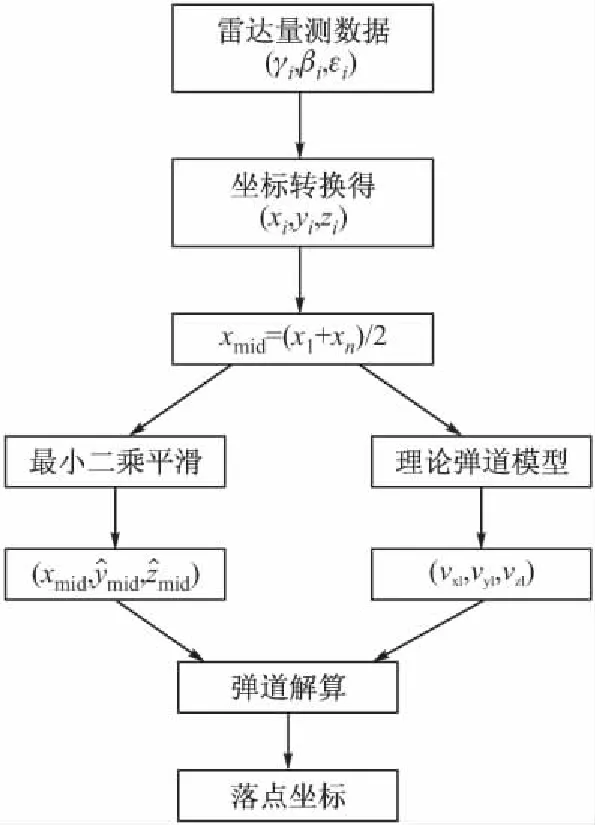
图3 结合理论弹道的落点预测算法流程

3.2 加权预测算法

当雷达测量数据较少时,滤波估计的误差波动较大,落点预测精度较差,因此只采用3.1节所提出的方法进行落点预测;当测量数据逐渐增多时,滤波估计的误差逐渐收敛且波动减小,这时,将非线性滤波预测方法和3.1节结合理论弹道的落点预测方法同时进行,将两种方法预测的结果进行加权平均。落点预测算法与雷达采样点数关系如图4所示。设非线性滤波落点预测结果为Rf,其对应权值为Wf;结合理论弹道的落点预测结果为Rl,其对应权值为Wl,满足Wf+Wl=1,则最终的落点预测结果为:

R=RfWf+RlWl

(6)

通过对预测结果的加权平均处理,减小非线性滤波在雷达采样数据较少时的预测偏差,提高落点预测的准确度。

对于几种算法权重的取值作如下规定:

(7)

4 算例仿真及分析

以某120 mm迫击炮弹为例,通过弹道方程组解算出炮弹飞行弹道数据,经雷达坐标转换后加入噪声,模拟雷达实际获得的测量数据,利用该数据对上述炮位与落点预测方法进行仿真计算。

4.1 炮位预测仿真

仿真条件为:炮弹初速300 m/s,射角45°,炮位与雷达站距离6 000 m,炮位相对雷达站方位33 mil,炮位与雷达站高程差50 m,雷达采样间隔为0.2 s,炮弹出炮口后4 s雷达开始跟踪,雷达系统的测量误差为σr=10 m,σβ=2 mil,σε=2 mil。

同时采用非线性滤波算法和综合算法进行炮位预测,得到炮位预测误差与雷达采样点数之间的关系,为便于观察前几个雷达采样点的炮位预测误差,截取前20个采样点并作炮位预测误差曲线如图4和图5所示。

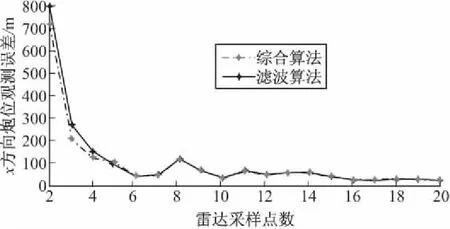
图4 x方向炮位预测误差

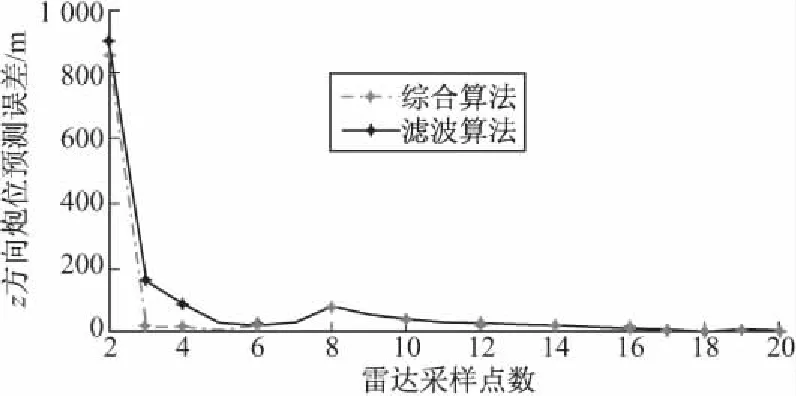
图5 z方向炮位预测误差

由图4和图5可以看出,在雷达获取前几个采样数据时,采用滤波算法外推炮位的误差较大,而采用上述分段算法,炮位预测的误差有一定程度的减小,且抛物线两点外推和最小二乘拟合算法简单,能够满足炮位侦察的快速性要求;当雷达采样点逐渐增多时,滤波算法的炮位预测误差迅速降低。因此,上述根据雷达采样数据个数而设计的分段预测方法,具有一定的工程参考价值。

4.2 落点预测仿真

落点预测的仿真条件为:炮弹理论初速300 m/s、实际初速306 m/s,射角为50°,射向0°,雷达相关采样参数同炮位预测仿真条件。令全弹道等效平均风为:wx=2 m/s、wz=2 m/s,其余按照炮兵标准气象条件计算。

按表1仿真条件,取分段采样点数分别为:n1=5,n2=15对上述落点加权预测算法进行仿真,并与单纯的非线性滤波落点外推结果进行比较,结果如表1所示。

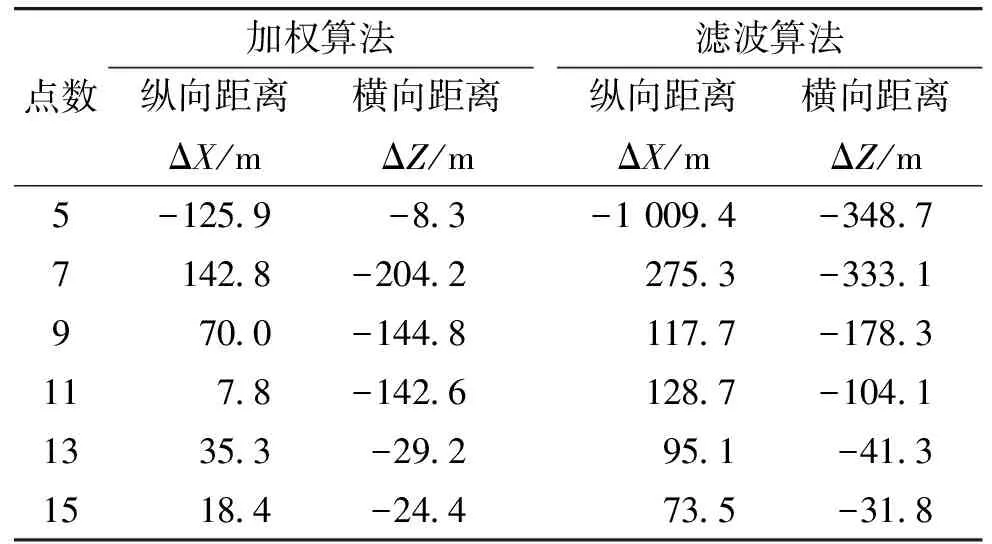
表1 加权算法落点预测坐标值比较

由表1可以看出,雷达采样点数较少时,滤波算法的落点预测误差较大;随着采样点数的增多,滤波算法的落点预测误差有所减小,但加权算法的预测误差要小于滤波算法。

由此可见,在雷达采样数据较少,不足以进行较为精确的滤波估计时,采用加权算法对炮弹的落点进行预测,能够获得比单独使用滤波估计更为理想的结果,且在雷达获取少量数据时便可开始预测落点,一定程度上满足了炮位侦校雷达数据处理的实时性要求,具有一定的工程参考价值。

5 结论

基于弹道理论,以雷达采样点数为分段依据,提出一种将抛物线近似、最小二乘拟合、非线性滤波三种方法进行分段综合的炮位快速预测算法;提出一种将理论弹道模型预测与非线性滤波预测加权综合的落点快速预测算法。以某120 mm迫弹为例进行仿真计算,仿真结果表明:

1)分段炮位预测算法能够在雷达获取两组测量数据时即开始预测炮位,实现炮位预测的快速性。

2)加权落点预测算法能够在雷达跟踪测量目标开始便进行落点预测,在雷达跟踪目标初始阶段能够获得比滤波算法更准确的预测结果。

两种方法较好的满足了炮位侦校雷达数据处理的快速性要求,但对于其他弹型以及有控弹丸,文中方法是否适用,还有待后续深入研究及完善。

[1] 唐吉祥,沈云山.卡尔曼滤波器在炮位侦察雷达中的应用 [J].电光与控制,2004,11(1):48-49.

[2] 杨荣军,王良明,修观,等.利用雷达测量数据的实际弹道重建 [J].弹道学报,2011,23(3):43-46.

[3] 李超旺,高敏,方丹,等.基于渐消记忆滤波的弹道修正弹落点预测 [J].弹箭与制导学报,2015,35(3):134-142.

[4] 胡献君,王航宇,周德超粒子滤波跟踪弹道下降段在炮位侦察中的应用 [J].现代防御技术,2013,41(1):104-109.

[5] 徐明友.高等外弹道学 [M].北京:高等教育出版社2003:174-178.

[6] KANDEPU R,FOSS B,IMSLAND L.Applying the unscented Kalman filter for nonlinear state estimation [J].Journal of Process Control,2008,18(7/8):753-768.

[7] 韩子鹏.弹箭外弹道学 [M].北京:北京理工大学出版社,2008:72-74.

[8] 何友,修建娟,张晶炜,等.雷达数据处理及应用 [M].北京:电子工业出版社,2006:42-47.

[9] 李云,陈春,刘玉文,等.利用有限的弹道参数外推炮位与炸点的数学模型 [C]∥中国兵工学会弹道专业委员会弹道学术交流会,2001:240-243.

ResearchonQuickPredictionofPointofFallandArtilleryLocationBasedonRadarMeasurement

CHEN Jianwei,WANG Liangming,LI Zijie

(School of Energy and Power Engineering,Nanjing University of Science and Technology,Nanjing 210094,China)

Aming at the problem that “First tracking,then prediction” lacked rapidity when using radar measured data to predict artillery location and point of fall,the artillery location prediction segmentation algorithm and point of fall prediction weighted algorithm was proposed,which used radar sampling points as piecewise parameters,and synthesized parabola approximation,lease square fitting,nonlinear filtering algorithms.A 120 mm shell was as an example for simulation,the result indicated that the artillery location prediction segmentation algorithm could start predicting after radar got two groups of measured data.The point of fall prediction weighted algorithm started predicting when the first measured data was got,meanwhile,the approach could acquire more accurate results when the sampled data was quite few compared with the nonlinear filtering algorithm.

radar data processing; nonlinear filtering; artillery location prediction; point of fall prediction

10.15892/j.cnki.djzdxb.2017.02.034

2016-05-11

陈健伟(1990-)男,江苏盐城人,博士研究生,研究方向:弹箭飞行与控制理论。

TJ012.3

A