基于调频傅里叶变换的低信噪比ISAR成像*

姜敏敏,张业荣

(1 南京信息职业技术学院,南京 210023; 2 南京邮电大学,南京 210003)

基于调频傅里叶变换的低信噪比ISAR成像*

姜敏敏1,张业荣2

(1 南京信息职业技术学院,南京 210023; 2 南京邮电大学,南京 210003)

针对LFM体制下ISAR雷达在低信噪比下对未知运动目标成像的难题,提出利用调频傅里叶变换的方法进行积累成像方法。在分析了脉间目标LFM回波信号特征的基础上,将目标回波信号在快慢时间域进行联合匹配和积累,通过能量积累后的目标位置估计搜索出目标的精确运动参数,并构建补偿函数实现目标运动补偿,从而获得低信噪比下的精确ISAR像。计算机仿真结果进一步表明了该方法能在低信噪比下稳健成像。

调频傅里叶变换;低信噪比;ISAR成像;运动参数估计

0 引言

地基飞行器探测一般是由窄带大功率探测雷达实现,但是为了有效识别目标还需利用成像雷达进行成像。一般成像雷达的作用距离低于探测雷达,如何在探测到目标之后尽快“提前”成像,有针对性地进行防御,是成像雷达需要进一步提升低信噪比下成像能力的一个动力。

采用线性调频(LFM)脉冲串的逆合成孔径雷达(ISAR)的成像方法基本可以分为脉冲相干累积方法(如R-D算法)和基于瞬时参数估计的瞬时成像方法(如各种时频分析算法)两类。而瞬时成像算法通常只利用一个或少数几个回波能量来成像,在低信噪比情况下将无法应用,所以只能求助于脉冲相干累积方法。

如果目标回波信噪比很低,ISAR雷达必须相干累积较多的脉冲才能获得足够的信号能量,另外,积累时间长也能增大雷达观测角度,提高方位分辨率。当然,长时间积累过程中如果目标作复杂运动,将使成像算法中的运动补偿环节难以精确实现,所以文中针对平稳弱目标进行分析。

现有文献针对低信噪比累积成像方法主要有:改进的包络对齐方法[1]、基于Keystone变换校正距离走动的方法[2]、基于图像的处理方法[3-4]等。对于改进的包络对齐方法,其出发点是脉冲压缩包络特征能识别,只能应用于噪声不太强的情况。对于Keystone变换方法,由于Keystone变换对噪声不敏感,是较好的解决方法。但是Keystone变换有以下一些问题:只能初步对齐包络,不能解决相位误差,存在插值误差,无法估计目标速度等。所以Keystone变换方法应用有一定局限性。而图像处理方法必须基于图像信噪比不太低的情况下才能实现散射点的提取。

针对现有文献的不足,文中提出了一种快-慢时间联合调频傅里叶变换的低信噪比成像方法,该方法利用线性调频信号的特征,在快时间维通过调频率和频率的自动搜索,得到目标速度和位置估计,同时在慢时间维通过自动搜索调整脉冲间位置,使目标距离像“凝结”在初始时刻位置上,最终可以完成若干个脉冲的能量累积。该方法的优点在于:不需要进行运动补偿和包络对齐处理;能同时完成成像和运动参数估计;对线性调频信号而言是一种线性化方法。

该算法虽然是一种二维参数搜索方法,但可以通过由粗到精的循环估计方法有效降低运算量。通过文中的分析可知,该算法的实际运算量不大,能满足工程需求。

1 调频傅里叶变换的定义

调频傅里叶变换[5]是匹配傅里叶变换[6]的一种极坐标表示方法,由于其变换核是线性调频函数,所以对于线性调频信号而言是一种线性变换。

对于一个二次相位信号:

s(t)=exp[j2π(fct+0.5γt2)]

(1)

式中：载波频率fc和调频率γ是信号参数。

其调频傅里叶变换为:

(2)

式中：f和μ是调频傅里叶变换的参数。

可以看出,在调频傅里叶变换生成的f-μ谱图中,当f=fc,μ=γ时,出现信号的相参积累峰值,其实质是通过线性调频形式的变换核去自动匹配待解信号,在参数完全匹配情况下能量达到峰值。

离散调频傅里叶变换的计算可以分两步进行,首先构造调频信号和二次相位信号相乘去调频,然后通过FFT得到离散调频傅里叶变换结果。如果调频率参数搜索个数为M,则其计算的主体部分就是M次FFT,所以其计算量不高。

2 联合调频傅里叶变换的构建

ISAR雷达发射LFM脉冲串,一个具有P个散射点的目标反射的回波信号可以表示为:

(3)

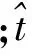
对于平稳飞行目标而言,在整个累积时间内目标相对雷达视线的转动角度很小,在目标尺寸不大的情况下,由转动引起的散射点径向位移相对于由径向速度引起的位移来说是很小的,对于平动补偿而言可以不考虑。那么只考虑目标径向运动情况下,Rim可以在全时间下表示为:

(4)

式中:tm为慢时间;Ri0为第i个散射点在初始时刻相距雷达的径向距离;v为目标径向速度。

去斜参考信号可以表示为:

(5)

式中：Rref为参考距离。Rref的获得对于宽、窄带交替ISAR雷达而言可以通过窄带雷达跟踪搜索得到,而对于单一宽带ISAR雷达而言必须通过目标速度估计来跟踪获得。在极低信噪比下,单一宽带ISAR雷达通过常规方法将很难能实现目标运动参数估计和跟踪。需要说明的是,文中算法在联合调频傅里叶变换的有效累积脉冲中设置固定的初始参考距离,以保证参考距离在累积脉冲中没有误差。

将回波信号和参考信号进行差频处理得到的差频信号为式(6)所示。

(6)

可以看出,差频后的信号在一个脉冲持续时间内,是关于快时间的二次相位信号,且其中存在的未知量为目标的速度和散射点的径向距离,那么可以设置速度和距离为待搜索参数去进行调频傅里叶变换,在速度和距离估计准确时可以得到积分的峰值。而从慢时间来看,各个脉冲的差频信号只是由于目标运动速度导致信号在频率项和初始相位项产生变化,而信号结构不变。所以,对于M个脉冲而言,整体的未知参数同样只有速度和散射点距离,那么可以构想将M个脉冲联合进行调频傅里叶变换,一样可以得到相应的速度和距离的二维参数估计。这样联合M个脉冲进行调频傅里叶变换,就可以充分利用M个脉冲的能量进行积累,理论上使参数估计的信噪比提升了M倍。

从这个思路出发可以构造一种快-慢时间联合调频傅里叶变换如式(7)所示。

(7)

经过这样的变换,从u-w的二维分布中就相应可以得到v和Ri0的估计。在该积分公式中可以看出,由于变换核是线性调频函数,只对差频信号s1中的线性调频函数分量进行能量匹配累积,而对s1中的噪声分量不存在能量匹配,所以信噪比相当于提升了M倍。且该公式表明,由于同时利用了幅度和相位信息,信号能量能完全匹配,可以达到信噪比的极限。

3 应用联合调频傅里叶变换的ISAR成像算法

根据前文的分析,可以构造出在极低信噪比下,联合快-慢时间维数据进行调频傅里叶变换的ISAR成像算法。对于单一宽带ISAR,其算法步骤描述如下:

1)假定ISAR雷达总观测脉冲数为N,根据信噪比改善需求,从N个脉冲中选取前2M个,构成联合调频傅里叶变换的累积脉冲。针对一定的成像空域,构造一个固定的初始参考距离,在所有回波中都采用该参考距离形成去斜参考信号,这样可以保证联合调频傅里叶变换的累积脉冲参考距离准确。对这2M个回波脉冲逐个进行差频处理,得到2M个差频信号。

2)根据式(7)构造前M个差频信号的快-慢时间联合调频傅里叶变换。通过变换可以得到这M个回波期间的平均速度v和第一个回波时刻目标距离Ri0的估计。这一步实际上得到了M个脉冲能量的累积,所以信噪比理论上可以提高M倍。

3)选取第2～(M+1)个差频信号,重复上一步的处理,就可以得到第2～(M+1)个回波期间的平均速度v和第二个回波时刻目标距离Ri0的估计。

(8)

(9)

可以看到式(9)的第一个指数项通过傅里叶变换后就是目标的距离像,而第二个指数项则对应方位向成像。可见通过上面的补偿已经消除了由于目标运动速度引起的脉内走动。

6)将前M个补偿后的差频信号逐个进行傅里叶变换,可以得到相应的M个目标距离像,这些距离像的位置其实是和联合调频傅里叶变换得到的M个目标距离Ri0的估计是一一对应的。当然这些直接傅里叶变换距离像信噪比很低,是完全淹没在噪声中的。

7)将上一步得到的M个距离像依据第4)步得到的目标运动轨迹,进行插值移位,即实现了前M个距离像的包络对齐。

8)将前M个包络对齐后的信号在慢时间维进行傅里叶变换,就可以得到目标的二维ISAR像。

以上步骤得到了前2M个脉冲中前M个的相干累积成像结果。对于后续的成像,同样以2M个脉冲为单位,按照以上的成像算法便可得到相应成像结果。

对于宽、窄带交替体制雷达而言其成像方法和前述步骤一致,同时由窄带雷达提供的参考距离和目标速度粗估计,可以缩小算法参数搜索范围,减小运算量。

文中提出的算法解决了极低信噪比下脉冲能量的相干累积,且可以实现目标成像和运动参数估计。

4 算法复杂度分析

文中算法的主体部分是利用调频傅里叶变换实现目标运动参数估计。所以以下主要分析目标参数搜索的计算量。

根据式(7),对于N点采样信号的调频傅里叶变换计算量约为N次复数乘法。

对于目标参数搜索来说,文中提出的调频傅里叶变换方法是要进行距离和速度的二维参数搜索,搜索量由距离和速度搜索范围大小和精度确定。例如,速度搜索窗为100 m/s、搜索精度为1 m/s和搜索距离窗为100 m、搜索精度为1 m的搜索,信号采样点数N取1 024,则计算量约为100×1 024×1 024次复数乘法,显然这个计算量较高。

但是由于文中的调频傅里叶变换方法是两个参数的估计,可以通过两个参数循环估计方法有效降低计算量。比如:可以先在距离区间固定一个距离值,以10 m/s的速度精度离散距离区间,即速度区间离散10个点,这样的调频傅里叶变换计算量约为10×1 024次复数乘法;然后利用估计出的速度值固定速度,且以10 m的距离精度离散距离区间,即距离区间离散10个点,这样的调频傅里叶变换计算量约为10×1 024次复数乘法;下一步,利用估计出的距离值固定距离,且以1 m/s的速度精度离散速度估计值附近的20 m/s范围,离散出20个点,这样的调频傅里叶变换计算量约为20×1 024次复数乘法;利用估计出的速度值固定速度,且以1 m的距离精度离散距离估计值附近20 m的范围,离散出20个点,这样的调频傅里叶变换计算量约为20×1 024次复数乘法。通过这种方法,总的计算量从约100×100×1 024次复数乘法变为了约60×1 024次复数乘法,计算量得到了大大降低。当然该方法会带来一定的能量失配,但其失配程度很低,并不会影响算法的信噪比性能。

同时该方法没有包络对齐或Keystone插值等运算量大的步骤,且方法本身运算量不高,总体成像时间可以得到保证,能满足工程需求。

5 仿真分析

在以下的仿真实验中采用以下雷达参数,雷达发射LFM脉冲串,其中心频率为f0=10 GHz,脉冲持续时间T1=5 μs,采样点数N=1 000,带宽B=500 MHz,脉冲重复周期T2=500 μs,总观测脉冲数M=400。在文中仿真中,每个雷达回波被添加了一定量的白噪声。

实验1联合调频傅里叶变换的性能分析

雷达对如图1所示的一个十字架目标成像,目标初始距离R0=50 km,径向速度v=5 000 m/s,绕中心点转动速度4°/s。

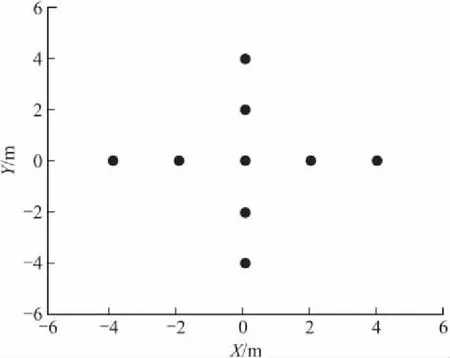
图1 目标形状

图2 SNR=30 dB时目标的速度和位置估计

SNR=30 dB时,对于前200个脉冲的差频信号利用式(7)进行联合调频傅里叶变换得到的目标速度和位置估计结果如图2所示。图3显示了SNR=30 dB时,第一个脉冲的去斜脉压结果。图2的含义是通过200个脉冲能量累积得到的速度和目标第一个脉冲时刻的位置估计,由于目标位置的估计消除了由高速运动引起的脉内走动,所以目标位置估计是精确的,而脉冲压缩结果出现了由于高速引起的位置偏移。同样可以看出在高信噪比下速度的估计也是很精确的。联合调频傅里叶变换还带来了一个额外好处,即在距离向能量较小的点与能量较大的点的幅度差相比脉冲压缩的幅度差小得多,弱散射点更易凸显出来。

图3 SNR=30 dB时脉冲压缩结果

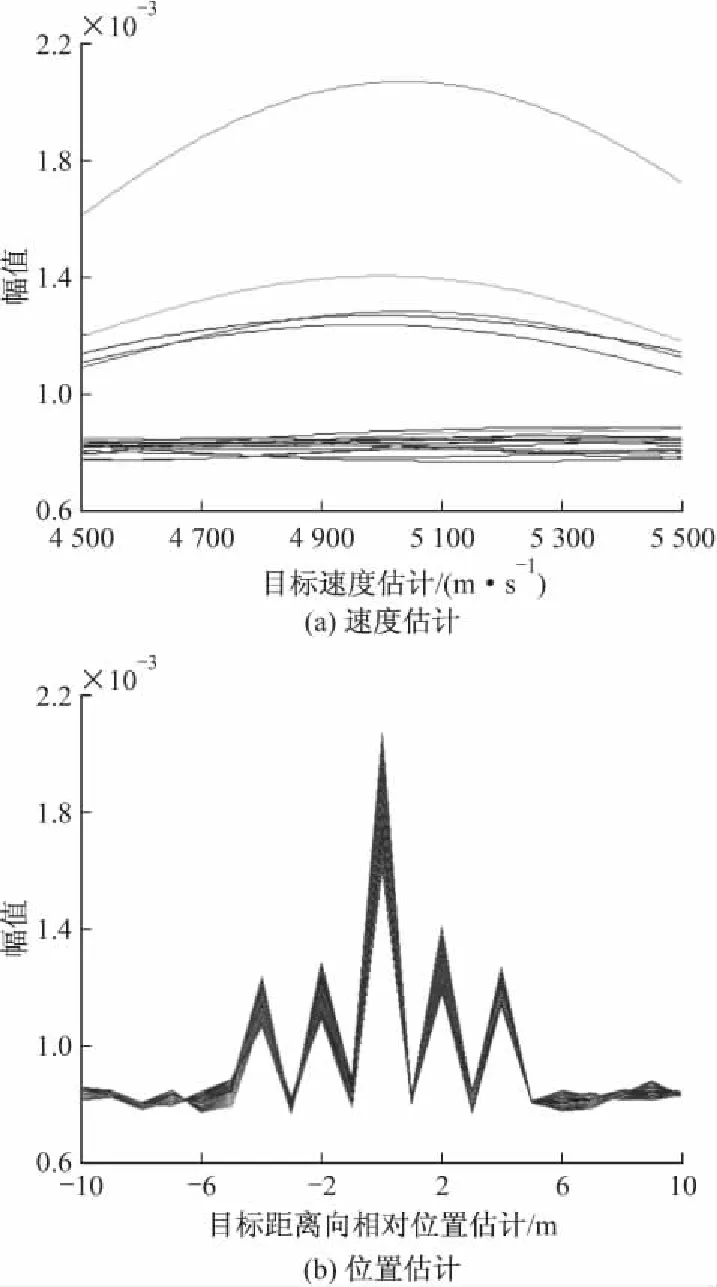
图4 SNR=-20 dB时目标的速度和位置估计

SNR=-30 dB时,对于前200个脉冲的差频信号利用式(7)进行联合调频傅里叶变换得到的速度和目标位置估计结果如图4所示,此时目标的速度估计出现了一些偏差,而目标位置估计精确。图5显示了SNR=-30 dB时,第一个脉冲的去斜脉压结果。对比图4和图5,在此信噪比情况下,去斜脉冲压缩结果已经分辨不出目标的真实位置了,而目标位置的估计则由于200个脉冲能量累积的改善而显得非常清楚。这充分显示了文中的联合调频傅里叶变换方法对于信噪比的改善能力。

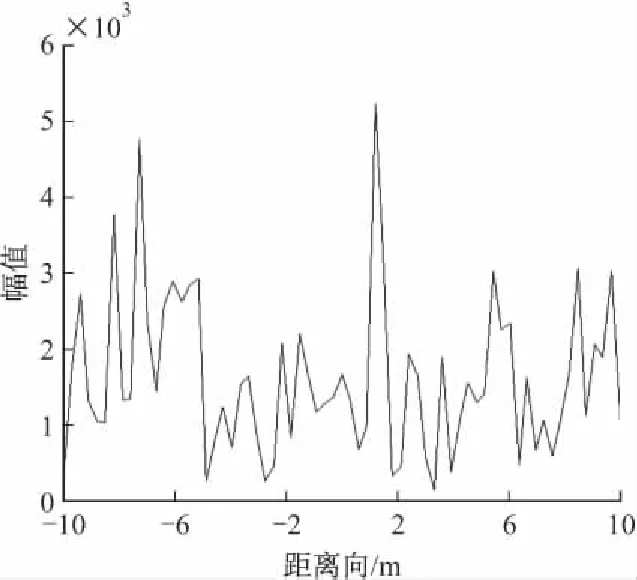
图5 SNR=-20 dB时脉冲压缩结果

根据文中提出的应用调频傅里叶变换的ISAR低信噪比成像算法,在SNR=-27 dB时,可以得到如图6所示的成像结果。可以看到成像结果能清晰分辨出目标,说明文中算法是正确的。

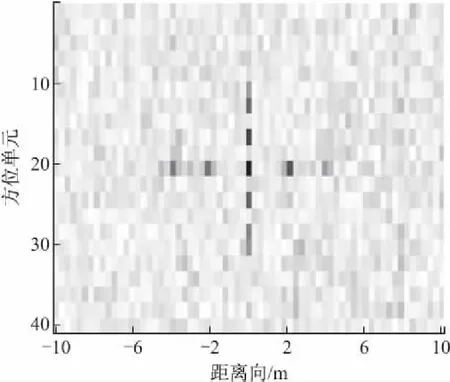
图6 SNR=-27 dB时目标的成像结果

实验2文中算法与其它文献的对比

雷达对如图7所示的一个飞机目标成像,目标初始距离R0=50 km,径向速度v=5 000 m/s,绕中心点转动速度4°/s,定义差频信号的信噪比SNR=-18 dB。

图7 目标形状

为了证明文中算法的优越性,与文献[2]和文献[3]的方法进行了比较。

对于文献[2],对前100个脉冲进行处理,其方法是先通过Radon变换估计目标初速度,消除多普勒模糊;用Keystone变换校正线性距离走动,得到对准的距离像;对各距离单元利用修正的离散调频傅里叶变换(MDCFT)结合逐次消去(CLEAN)方法得到多普勒像。该方法得到的是图8所示成像结果,可以看出该方法在SNR=-18 dB时可以从图像中分辨出目标。

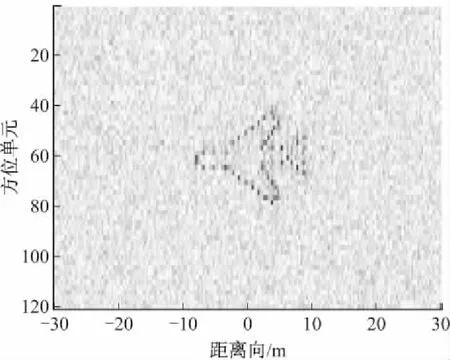
图8 文献2成像结果

对于文献[3],对于前100个脉冲进行处理,其方法对于回波直接采样信号,利用二维ISAR图像熵为目标函数,结合阻尼牛顿法进行最优化求解,以完成平动分量的估计。该方法得到的是图9所示成像结果,可以看出该方法在SNR=-18 dB时不能成像,这是因为该方法以图像熵为衡量标准,在低信噪比下无法正确收敛,所以得不到成像结果。

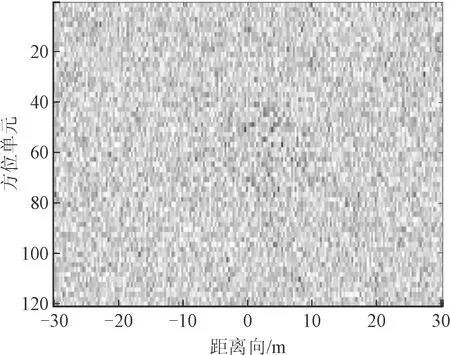
图9 文献3成像结果

对于文中方法,对于前200个脉冲进行处理,得到的是图10所示成像结果,可以看出其成像信噪比很高。通过和文献的比较,可以看出文中方法的抗噪性能最强。

图10 文中算法成像结果

6 结论

采用LFM脉冲的ISAR雷达要在低信噪比下获得成像结果,必须对脉冲压缩结果进行相干累积。文中通过构造快-慢时间联合调频傅里叶变换,获得了比现有文献更高的信噪比性能,实现了平稳目标在极低信噪比下的相干累积ISAR成像和跟踪。

[1] 刘志凌,廖桂生,杨志伟.低信噪比条件下一种迭代加权拟合的ISAR包络对齐方法 [J].电子学报,2012,40(4):799-804.

[2] 陈文驰,刘飞.一种低信噪比下的ISAR成像实现方法 [J].电波科学学报,2010,25(3):585-589.

[3] 杨磊,熊涛,张磊,等.低信噪比联合自聚焦ISAR成像平动补偿 [J].西安电子科技大学学报,2012,39(6):70-78.

[4] 张龙,张磊,邢孟道.一种基于改进压缩感知的低信噪比ISAR高分辨成像方法 [J].电子与信息学报,2010,32(9):2263-2267.

[5] 付耀文,胡杰民,黎湘.基于调频傅里叶变换的匀加速转动目标ISAR成像 [J].系统工程与电子技术,2011,33(12):2608-2612.

[6] 王盛利,李士国,倪晋麟,等.一种新的变换-匹配傅里叶变换 [J].电子学报,2001,29(3):403-405.

ISARImagingBasedonFrequencyModulatedFourierTransforminLowSNREnvironment

JIANG Minmin1,ZHANG Yerong2

(1 Nanjing College of Information Technology,Nanjing 210023,China; 2 Nanjing University of Posts and Telecommunications,Nanjing 210003,China)

In order to obtain the unknown motion target imaging under low SNR in the LFM system,a new accumulation imaging method based on frequency modulated Fourier transform was proposed.Based on the characteristics of the target’s LFM radar interpulse echo signals,the target’s echo signals were jointly matched and accumulated in fast-slow time domain.Through the target position after energy accumulation,the target’s accurate motion parameters could be searched out.After that,the compensation function was constructed to compensate the target motion,so as to obtain the accurate ISAR image.Computer simulation results showed that the proposed method could be robust under low SNR.

frequency modulated Fourier transform; low SNR; ISAR imaging; motion parameter estimation

10.15892/j.cnki.djzdxb.2017.02.032

2016-04-01

国家自然科学基金(61071022),江苏省高校品牌专业建设工程资助项目(PPZY2015A092)资助

姜敏敏(1983-),女,安徽蚌埠人,讲师,硕士,研究方向:雷达信号处理。

TN958.3

A