一种变形翼的气动特性数值模拟研究*

王贤勇,何小辉,雷娟棉,余少文

(1 江南工业集团有限公司,湖南湘潭 411207; 2 北京理工大学,北京 100081)

一种变形翼的气动特性数值模拟研究*

王贤勇1,2,何小辉1,雷娟棉2,余少文2

(1 江南工业集团有限公司,湖南湘潭 411207; 2 北京理工大学,北京 100081)

为研究可变形翼在动态变形过程中的气动特性,文中利用数值模拟软件FLUENT中的动网格技术,模拟了可变形翼在不同变形速度下的变展长、变后掠和变翼型等变形过程的气动特性。结果显示翼的不同变形方式和变形速度对翼的气动特性产生不同的影响,变展长受变形速度的影响不大,而变后掠和变翼型对变形速度比较敏感。分析结果对可变形飞行器的研究具有重要的意义。

可变形翼;气动特性;变展长;变后掠;变翼型

0 引言

传统的飞行器发展很快,但由于几何形状基本不变,所以只能完成一些单一的任务。然而技术的飞速发展使得我们对飞行器的多功能化要求也在不断提高,因此可变形飞行器应运而生。可变形飞行器是一种全新概念的多用途、多形态飞行器,它能够根据飞行环境和作战任务等的需要进行自适应变形,以发挥飞行器最优的飞行性能[1]。与现有飞行器改变控制面的传统方法不同,它可以有效地实现外形的光滑连续变形。可变形飞行器的构想主要来源于仿生,精髓是集成[2]。高新技术的基础研究和技术的进步,尤其是微电子、计算机与信息处理、隐身技术、复合材料以及航空航天等高新技术的快速发展,为可变形飞行器的研究奠定了基础[3]。

文中采用数值模拟的方法,研究了可变形翼在变形过程中的气动特性,旨在探讨可变形翼在连续变展长、变后掠和变翼型过程中变形对自身气动特性的影响。

1 计算方法

文中求解的是定常和准定常雷诺平均N-S方程组,用有限体积法对控制方程进行离散,采用耦合解算技术进行求解,并应用多重网格技术加速收敛。

1.1 基本方程

将积分形式的Navier-Stokes方程写为:

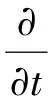
(1)

式中:W、F和G定义为:

矢量M为源项。其中ρ、v、E和p分别为密度、速度、单位质量的总能和流体压力;τ为黏性应力张量;q为热流通量。E与H的关系为:

E=H-p/ρ

(2)

其中:

H=h+|v|2/2

(3)

1.2 湍流模型

湍流模型采用S-A模型:S-A(Spalart-Allmaras)模型是一个相对简单的一方程湍流模型,是为了涉及壁面约束流动的航天应用而特别设计的,对有逆压梯度的边界层显出了良好的计算结果。

S-A模型不必计算与当地剪切层厚度相关的长度尺度,而且在壁面附近不需要非常精细的网络,只需与代数模型相当的网格即可,因此计算比较容易。此外,S-A模型中输运变量的近壁梯度远小于κ-ε模型中输运变量的梯度,这使得当非层状网格用于近壁时模型对数值误差不太敏感。

S-A模型的输运方程:

(4)

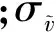
1.3 动网格技术

可变形翼的变展长、变后掠和变翼型等变形过程是连续的,为了使数值模拟更接近于真实,在数值模拟的过程中,采用了动网格技术使可变形翼的三维模型在计算过程中实现连续变形。

文中通过UDF调用网格变化的宏使得可变形翼的轮廓连续变化,同时采用两种网格重构方法(光顺法和局部重构法)对变形区域的网格进行重构。

2 变形翼机构

为了验证可变形翼在翼型、后掠角(或前掠角)以及展长三方面都可以实现主动变形的可行性,文中设计出了一种可变形翼的变形机构。

如图1所示,弦向梁上下表面整齐布满可任意伸缩的柱形结构,这种柱形结构可以在程序的控制下以某种速度达到需要的长度。

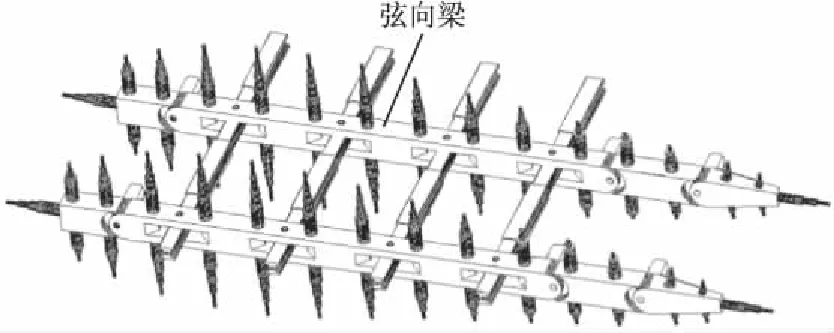
图1 变形机构单元结构图

如图2所示,通过展向梁内部伸缩机构的动作,使得展向梁单元伸长或收缩,从而实现可变形翼的展长变化。

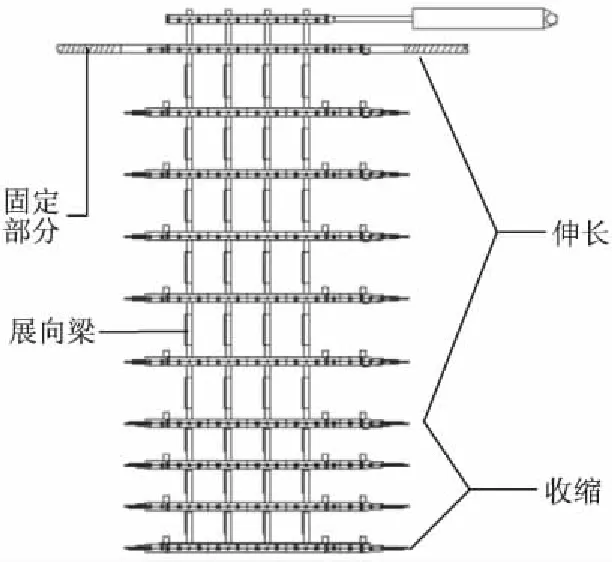
图2 变展长结构图

如图3所示,通过控制变后掠液压缸的伸缩,使得展向梁与弦向梁相对转动,从而实现可变形翼的后掠(或前掠)角的变化,且后掠(或前掠)角的变化量等于弦向梁和展向梁之间夹角的改变量。

图3 变后掠结构图

如图4所示,当前后缘的弦向梁转动时,翼型就会出现相应的弯度;当弦向梁上的伸缩杆装置依照程序伸缩时,翼型就会有相应的变形。

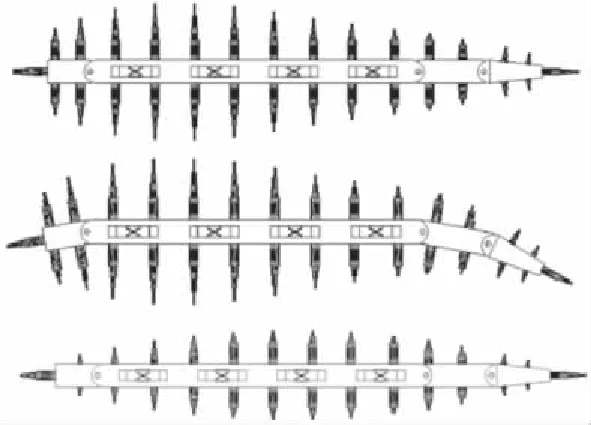
图4 变翼型结构图

3 数值模拟

3.1 可变形翼变展长的数值模拟

对如图5所示的具有亚声速翼型(NACA0012)的翼面进行了展长连续非定常变化过程绕流场的数值模拟[4],通过程序控制翼在模拟计算的过程中能够以某一速度增加展长,这里采用的速度是0.035 m/s。计算域采用非结构网格离散,在翼面展长变化的非定常流场模拟过程中,通过网格的变形、重构实现对动态变化流场域的离散。

图5 可变展长的三维翼

图6和图7分别给出了三种不同马赫数下翼面展长逐渐增大时其升、阻力系数的变化曲线。由升力系数曲线可知,随着展长的连续增大,三种不同马赫数下的升力值也在连续增大,这有两个原因:一是由于展长增加,弦长不变,则展弦比增加,所以升力系数导数增加,从而升力系数增大;二是由于展长增加,弦长不变,翼面积增加,从而升力系数增大[5]。因此飞行器需要较大升力时,可将展长增大,比如飞行器在起飞阶段时,可将展长增加到最大,从而可获得较大的升力,减小了起飞距离,起飞后再将展长相应减小,从而减小阻力,降低能耗,增加航程。

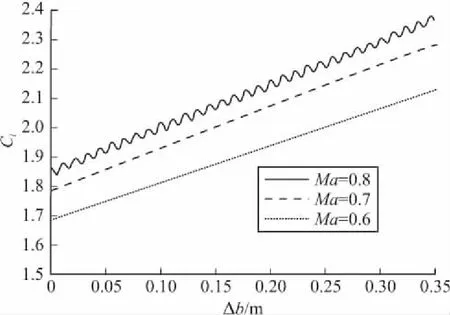
图6 升力系数随展长变化量的变化曲线

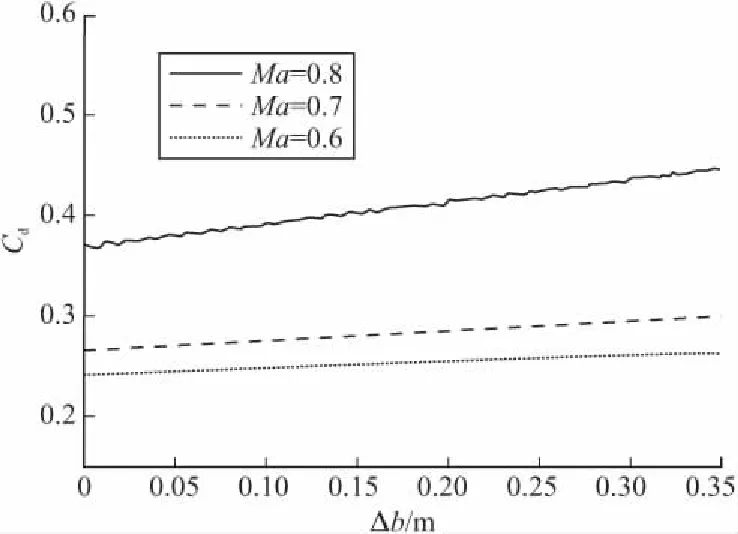
图7 阻力系数随展长变化量的变化曲线

3.2 可变形翼变后掠角的数值模拟

可变后掠翼的飞行器很早就存在了,但是它们的翼都是刚性变形的,这样就存在一个缺点,即当后掠角改变后,由平行于来流方向的平面切割翼所得到的翼型也发生了改变,从而使得对气动特性的控制变得更加复杂。

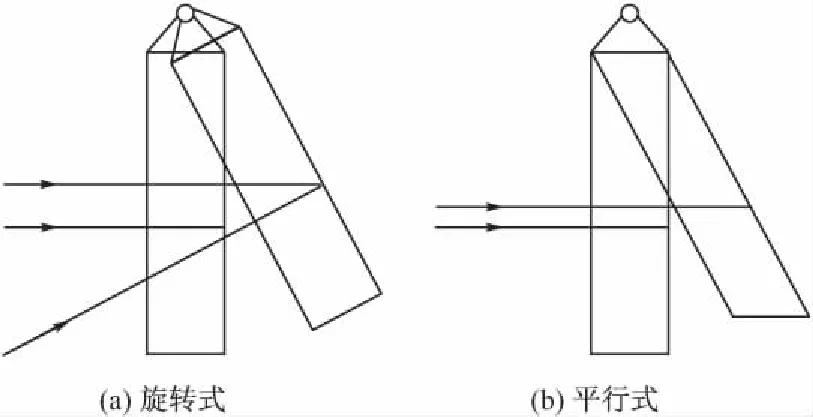
图8 两种不同变后掠方式的平面示意图

文中采用的可变形翼的机构,是通过翼自身形状的变化来改变后掠角的大小,且平行于来流方向的平面切割翼所得到的翼型并不发生变化(如图8),从而对气动特性的控制大大简化[6]。

翼型采用的是六角形翼,后掠角最大为45°,来流Ma=1.5,攻角α=4°,变后掠采用两种角速度,分别为ω=78.540 rad/s和ω=7.854 rad/s。在数值模拟计算过程中,通过程序来控制网格点的运动(如图9)。

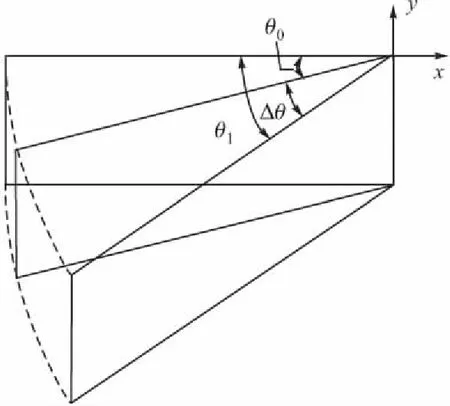
图9 翼面后掠角变化过程示意图

(5)

θ0=ω×t

(6)

θ1=θ0+Δθ

(7)

(8)

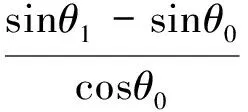
(9)

z1=z

(10)

式中:dt为非定常数值模拟计算的时间步长;t为非定常数值模拟计算的总时间;x、y、z为翼上任意某一点的坐标值,通过编程,利用式(8)、式(9)和式(10)来控制翼上网格点的坐标变化,从而控制网格点的运动。

图10和图11分别给出了翼面在两种后掠角变化速度下,翼的升力系数变化曲线和阻力系数变化曲线。由图10和图11可以看出在变形较慢的情况下,升力和阻力随着后掠角的增大变化较平滑,而在变化较快的情况下,变形开始和结束时升力和阻力都有明显扰动,这是因为翼在变后掠的过程中会引起来流相对于翼的速度的变化,而且翼从一种外形变化到另外一种外形时,建立相应的流场也需要时间。

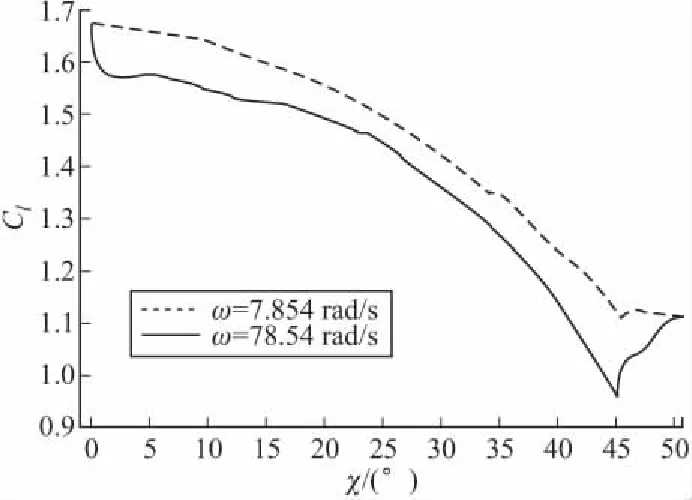
图10 翼面升力系数随后掠角变化量的变化曲线

图11 翼面阻力系数随后掠角变化量的变化曲线

翼的弦长为1 m,展长为3 m,在ω=78.54 rad/s和ω=7.854 rad/s两种不同变形速度下,翼尖处速度分别为V1=235.62 m/s和V2=23.56 m/s,来流速度为V∞=510 m/s,V1/V∞=0.462,V2/V∞=0.046,显然,V2相对来流速度较小,影响并不明显,而V1的大小接近来流速度的一半,此时翼尖相对来流的瞬时速度为274.38 m/s,从翼尖到翼根,前缘速度是不断减小的。且有:

(11)

式中:b为展长;l为当前点到翼根的横向距离。

因此,来流相对翼的整体速度明显减小,于是翼在刚开始变形时,升力和阻力会产生一个明显下降的扰动,变形结束时,升力和阻力又会有一个明显回升的扰动,从整个过程来看,变化过程中的升、阻力相对于变化较慢的准定长状态时的升、阻力是一个整体向下平移的效果。由此可见,变化速度较大时,在变形开始和结束时的升、阻力会有明显的扰动,从而会对飞行器飞行过程中的稳定性带来一定影响,若扰动大到某个程度,甚至会给飞行器带来失速坠机的危险,而变形速度太慢又有可能达不到变形本身的目的,因此,飞行器在变形时,选择一个最佳的变形速度非常重要。

3.3 可变形翼变翼型的数值模拟

文中对翼型由亚声速翼型(NACA0012)变为超声速翼型(双弧形翼型)的过程进行了非定常和准定常数值模拟,其中来流马赫数Ma=2.0,攻角α=4°,整个变形过程所用时间ΔT=0.1 s。

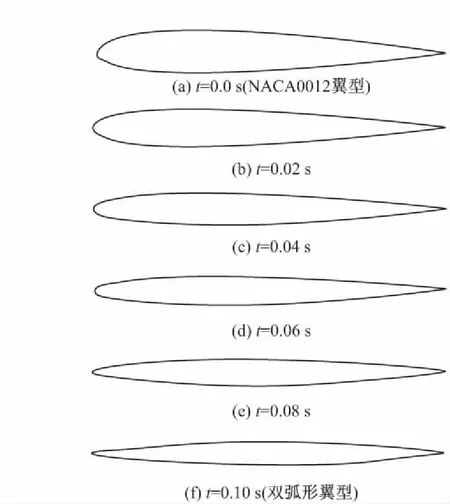
图12 亚声速翼型连续变为超声速翼型不同时刻翼型图

图12给出了翼型从亚声速的NACA0012翼型变为超声速双弧形翼型的变形过程中不同时刻的翼型图。图13为翼型从NACA0012翼型变为双弧形翼型非定常模拟和准定常模拟的升力系数变化曲线。从图中可以看出,随着翼型从亚声速翼型到超声速翼型的变化,翼型的升力系数总体呈增大趋势。这是因为翼型前缘产生了激波,随着翼型的变形,激波强度减弱,但是在攻角的影响下,上翼面激波强度的减弱速度快于下翼面激波强度的减弱速度,因此上翼面的压力减小的更快,使得升力增大。

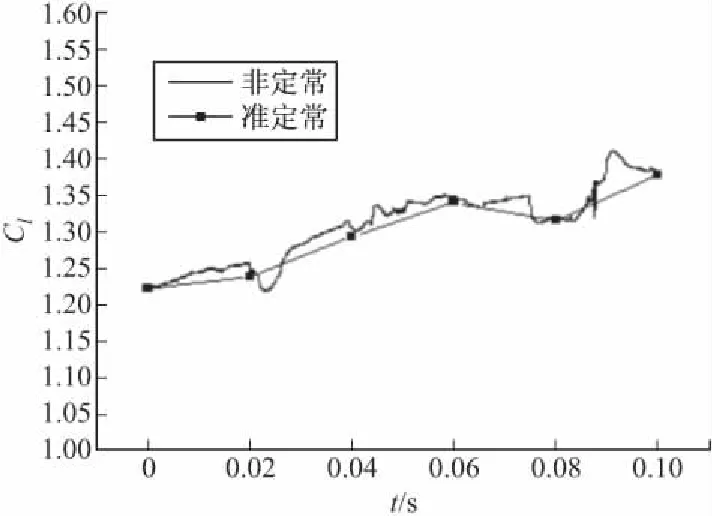
图13 升力系数随翼型变形的变化曲线(Ma=2.0,α=4°)

图14给出了翼型从亚声速翼型变为超声速翼型的过程中,非定常模拟和准定常模拟的阻力系数变化曲线。从图14中可以看出,随着翼型从亚声速翼型到超声速翼型的变化,翼型的阻力系数呈减小趋势。无论是脱体激波还是贴体激波,激波强度都在减弱,激波阻力减小,而激波阻力对翼型阻力起决定性作用,因而阻力随着激波阻力的减小而减小。

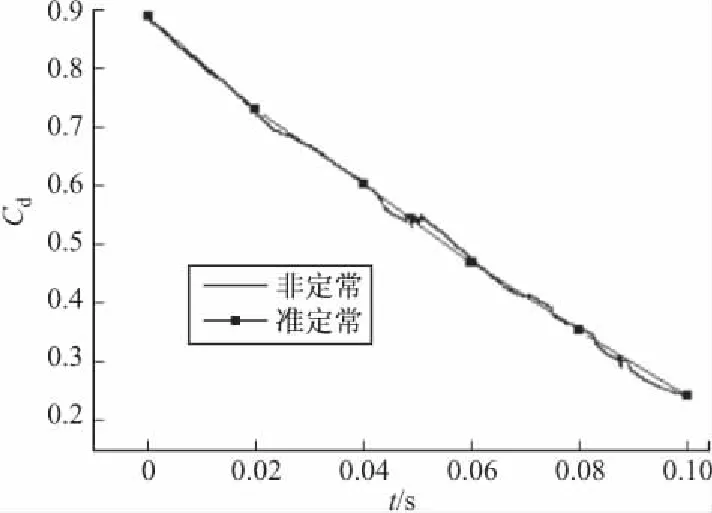
图14 阻力系数随翼型变形的变化曲线(Ma=2.0,α=4°)

从图13、图14中可以看出,翼型从亚声速翼型变为超声速翼型的过程中,非定常模拟的结果与准定常模拟的结果基本一致;但非定常模拟的升力系数与非定常模拟的阻力系数相比波动较大,因此升力系数受非定常变形的影响较明显。

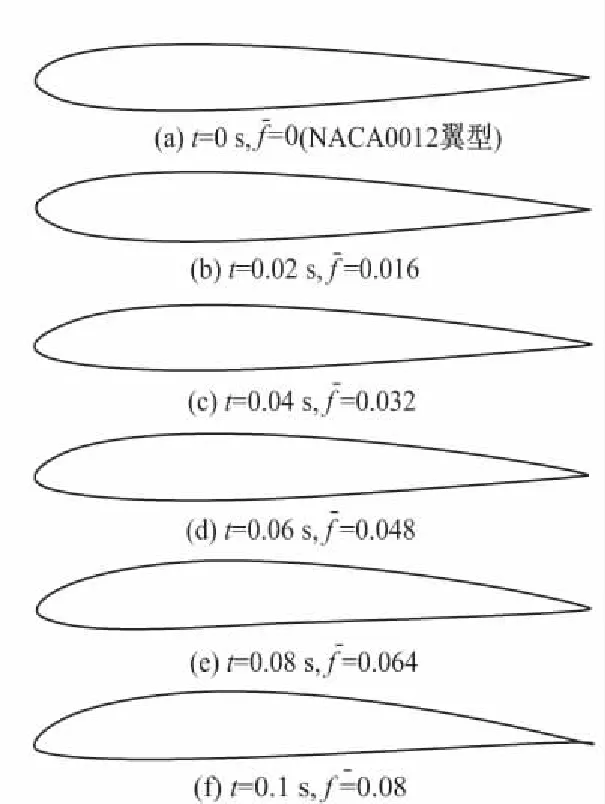
图15 亚声速翼型连续变弯度过程中不同时刻翼型图

图16给出了NACA0012翼型变弯度过程中非定常数值模拟和准定常数值模拟计算得到的升力系数变化曲线。从图16中可以看出,随着翼型弯度的不断增大,翼型的升力系数逐渐增大,升力特性变好。非定常变形得到的升力系数在变形的中前期比准定常得到的升力系数小,但在变形快结束时与准定常得到的升力系数趋于一致。

图17给出了NACA0012翼型变弯度过程中非定常数值模拟和准定常数值模拟计算得到的阻力系数变化曲线。从图中可以看出,随着翼型弯度的不断增大,翼型的阻力系数逐渐增大,阻力特性变差。两种变形方式下的阻力系数差别不明显。

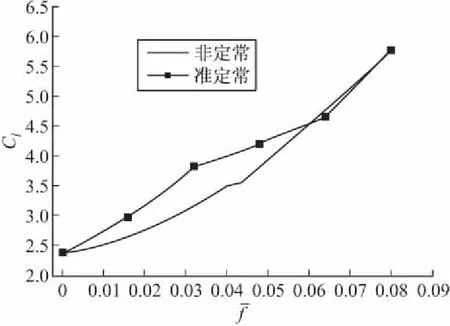
图16 升力系数随翼型弯度增大的变化曲线(Ma=0.6,α=4°)

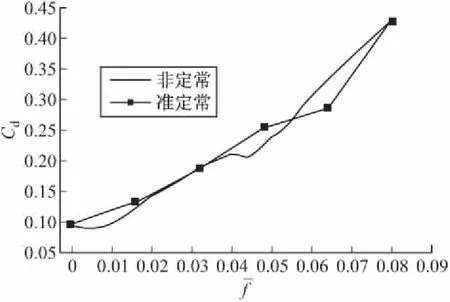
图17 阻力系数随翼型弯度增大的变化曲线(Ma=0.6,α=4°)

从图16、图17中可以看出,NACA0012翼型弯度增大的过程中,非定常数值模拟得到的升力系数比准定常数值模拟得到的升力系数要小;非定常数值模拟得到的阻力系数与准定常模拟得到的阻力系数基本一致。由此可知,非定常模拟得到的气动特性比准定常模拟得到的气动特性略差,翼型的变形速度对动态气动特性有不可忽略的影响。

4 结论

总结上述计算结果可得:

1)随着展长的连续变大,翼的阻力系数和升力系数都在连续增加,且低速连续变形时,可认为是准定常过程。

2)变后掠角变形对变形速度比较敏感,在较大速度下变形时,变形开始和结束阶段升、阻力会有较大的阶跃式扰动,对飞行器的稳定性有一定影响,因此,选用最佳的变形速度非常重要。

3)翼型做非定常变化时,升力系数对变形速度较敏感,阻力系数变化不大。

4)翼的不同变形方式和变形速度对翼的气动特性产生不同的影响,通过对可变形翼的有效控制,得到合适的实时气动特性是可行的,对可变形飞行器的研究具有一定的参考价值。

[1] JOSHI Shiv P,TIDWELL Zeb.Comparison of morphing wing strategies based upon aircraft performance impacts:AIAA 2004-1722 [R].2004.

[2] 李军府,艾俊强,董海锋.飞机变形技术发展探究 [J].航空科学技术,2009(2):3-6.

[3] 崔尔杰,白鹏,杨基明.智能变形飞行器的发展道路 [J].航空制造技术,2007(8):38-41.

[4] 陈钱,尹维龙,白鹏,等.变后掠变展长翼身组合体系统设计与特性分析 [J].航空学报,2010,31(3):506-513.

[5] LEITE A,VALE J，LAU F，et al.Development of morphing strategies for flight demonstrator RPV:AIAA 2009-2134 [R].2009.

[6] GANDHI N,COOPER J，WARD D，et al.A hardware demonstration of an integrated adaptive wing shapeand flight control law for morphing aircraft:AIAA 2009-5890 [R].2009.

[7] GRIGORIE T L，BOTEZ R M，POPOV A V.Adaptive neuro-fuzzy controllers for an open-loop morphing wing system:AIAA 2009-5893 [R].2009.

NumericalSimulationofAerodynamicCharacteristicsofaDeformableWing

WANG Xianyong1,2,HE Xiaohui1,LEI Juanmian2,YU Shaowen2

(1 Jiangnan Industries Group Co.Ltd,Hunan Xiangtan 411207,China; 2 Beijing Institute of Technology,Beijing 100081,China)

In order to study the aerodynamic characteristics of deformable wing in the process of dynamic deformation,the moving mesh technique in numerical simulation software FLUENT was used to simulate the aerodynamic characteristic of deformable wing at different deformation speed in different deformation process,such as variable span,variable sweep and variable airfoil.The results showed that different deformation mode and deformation speed of the wing had different impact on the aerodynamic characteristics of the wing,and variable span had little effect on deformation speed.The variable sweep and variable airfoil were sensitive to it.The analysis results were of great significance to the study of deformable aerocrafe.

deformable wing; aerodynamic characteristics; variable span; variable sweep; variable airfoil

10.15892/j.cnki.djzdxb.2017.02.029

2016-05-11

王贤勇(1984-),男,山东阳谷人,工程师,硕士,研究方向:可变形飞行器。

V211.41

A