基于ADAMS的无人机零长发射动力学仿真及分析*
2017-11-09杨龙军
石 林,马 威,杨龙军
(江西洪都航空工业集团有限责任公司,南昌 330024)
基于ADAMS的无人机零长发射动力学仿真及分析*
石 林,马 威,杨龙军
(江西洪都航空工业集团有限责任公司,南昌 330024)
针对无人机零长发射系统研制需要,以无人机零长助推火箭发射段为主要研究对象,利用ADAMS建立了无人机发射动力学仿真模型,分别对质心偏心和助推火箭推力偏心工况进行动力学仿真,获取了发射过程中无人机质心位移和角度的变化规律,分析了无人机与发射架的安全距离。结果表明:无人机质心偏心和推力偏心影响其运动姿态,且推力偏心的影响更明显,无人机在发射过程中能够安全离开发射架。
无人机;零长发射;仿真;模型
0 引言
无人机的快速发展引发了层出不穷的军事学术、装备技术等相关问题的研究,并在未来会有越来越广泛的应用[1]。火箭助推零长发射方式是地面发射无人机时用得较多的发射方式,该发射方式具有便捷、快速,对发射场地无严格要求,适合于野战环境等优点,与发射方式配套的发射系统同时由于体积小、机动性强、适应性强等特点,使其在无人机系统中具有重要而特殊的地位[2-3]。
对于研制阶段的无人机系统,开展零长发射试验来确定各种设计参数还比较困难,采用ADAMS仿真软件,以多体系统动力学理论为基础,把无人机和发射系统简化为多刚体系统[4],对无人机质心偏心和推力偏心工况进行发射动力学仿真,为验证无人机零长发射可行性和安全性提供了有效可行的方法,对无人机总体作战性能的提高具有重要的意义。
1 无人机零长发射系统介绍
无人机零长发射系统按照结构特点分为发射架和无人机两大部分。无人机机身前方和后部共有4个支撑轴约束在发射架上,无人机下方后端装有助推火箭,无人机零长发射系统如图1所示。发射架主要由发射架体、翻转机构、后支撑、剪切销机构等组成,其中发射架体是发射架的主承力件,为发射架各机构的安装平台,翻转机构是无人机前支撑轴约束点,后支撑是无人机后支撑轴约束点,当助推火箭达到一定的推力情况下,剪切销剪断,无人机脱离翻转机构的约束而离开发射架。
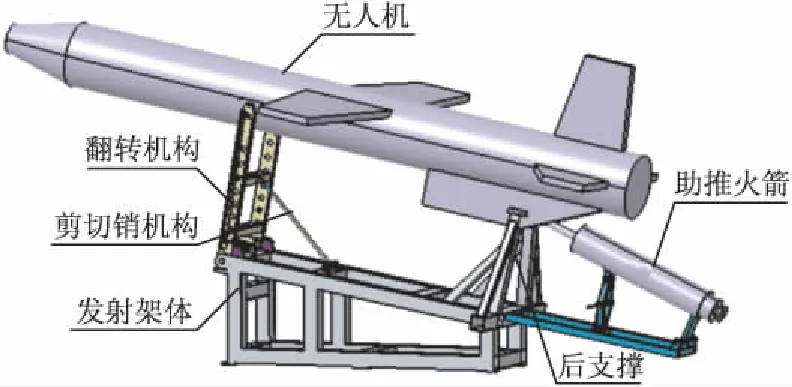
图1 无人机与发射架
2 无人机零长发射仿真模型
2.1 模型假设
为了研究问题的需要,计算中模型作了如下假设:
1)将无人机和发射架作为刚体,在运动过程中,形状、质量、质心都不发生改变[5];
2)仿真忽略助推火箭与无人机脱离现象;
3)不考虑振动问题,忽略发射架和无人机的振动;
4)不考虑风的影响。
2.2 模型导入及约束添加
将无人机与发射架的三维数模简化,然后导入ADAMS中,将无人机和发射架均作为刚体,添加约束条件,发射架体与大地固定连接,后支撑与发射架体固连,助推火箭和无人机作为一个整体,用固定副连接;剪切销机构转杆与发射架体之间为转动关系,翻转机构与发射架体之间为转动关系,用旋转副连接;由于无人机前、后支撑轴与翻转机构、后支撑之间相对运动时会发生碰撞,因此需要创建接触(contact)进行约束。
其中,以无人机质心为原点,以平行于地面的无人机行进方向为X轴,以垂直向上方向为Y轴,根据笛卡尔坐标系建立Z轴。在ADAMS中建立无人机的发射动力学仿真模型。
2.3 设置仿真参数
无人机发射仰角为10°,无人机轴线和助推火箭轴线夹角为13°,助推火箭推力按常温工作状态下的推力曲线进行加载,在ADAMS中推力加载调用格式为:AKISPL(time,0,SPLINE_CW,0)。
取翻转机构扭簧扭矩为17.5 N·m,取剪切销机构扭簧扭矩为1.8 N·m;闭锁力为4 000 N,根据推力曲线可知,靶机解锁时间约为0.005 s,将剪切销设置成固定副,利用仿真控制脚本语句来描述,控制描述语句为:SIMULATE/DYNAMIC,END=0.005,STEPS=10;DEACTIVATE/JOINT,ID=28。设置仿真时间End Time为0.5 s,仿真步长Steps为1000。
2.4 零长发射动力学方程的建立
ADAMS建模方法采用第二类拉格朗日方程,选取系统内每个刚体质心的笛卡尔坐标和确定刚体方位的欧拉角作为广义坐标,即:
则对每个刚体,建立对应于6个广义坐标带乘子的拉格朗日方程为:
完整约束方程时:f(q,t)=0
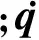
3 发射仿真结果及分析
3.1 无人机发射仿真结果
1)理想工况
在理想工况下,此时质心偏心0 mm,助推火箭推力偏心0′时,无人机质心的位移和角度随时间的变化规律,如图2和图3所示。
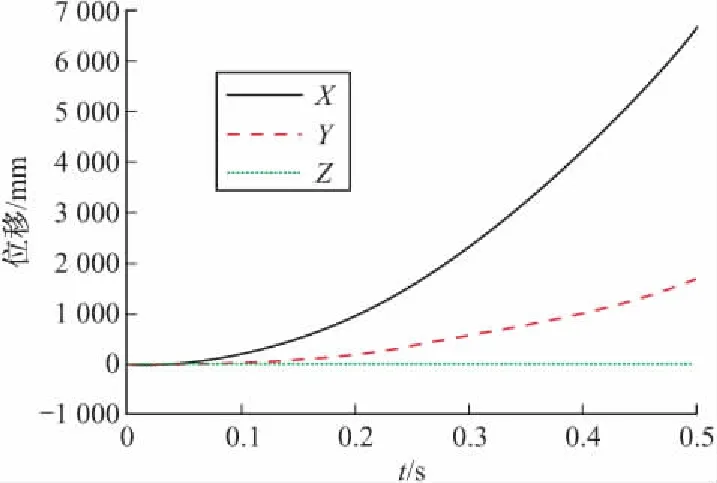
图2 无人机质心位移曲线
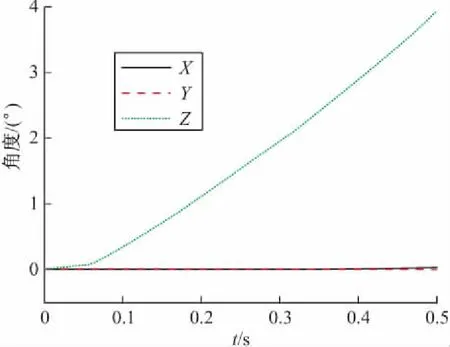
图3 无人机角度曲线
2)无人机质心偏心计算
分别取无人机质心侧向偏心0.2 mm、0.4 mm、0.6 mm工况,对其在0.5 s发射阶段进行动力学仿真,得出无人机发射过程中的位移和角度随时间的变化规律。仿真结果表明:随着无人机质心偏移距离的增大,无人机质心X、Y向位移的变化不明显,Z向位移偏移量随之增加;俯仰角的变化不明显,滚转角和偏航角的偏移量也随之增加。由于滚转方向转动惯量远小于偏航方向,使滚转角的偏移量大于偏航角,因此,质心偏心对滚转角影响更大。
Z向位移、滚转角和偏航角的变化规律如图4~图6所示。
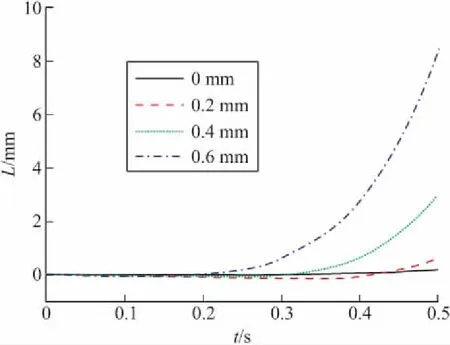
图4 无人机质心Z向位移曲线
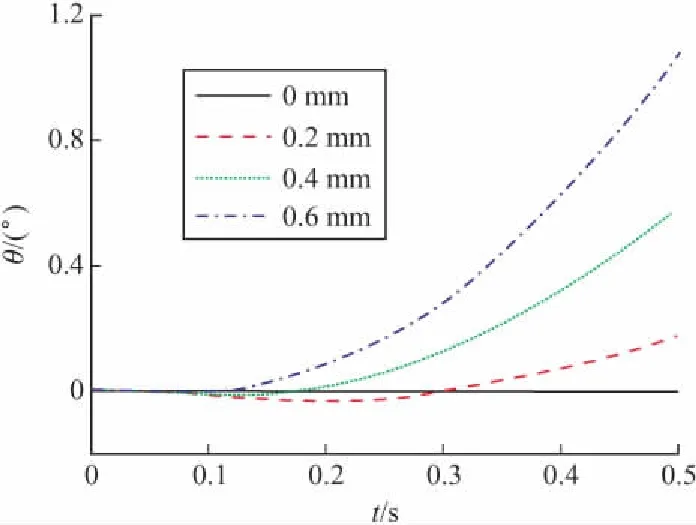
图5 无人机质心X向滚转角曲线
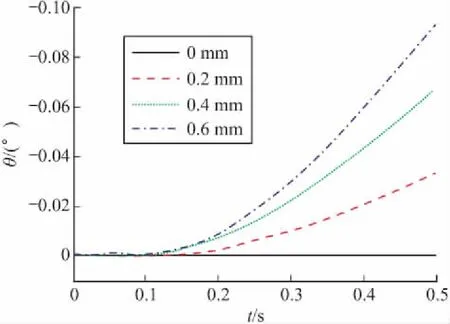
图6 无人机质心Y向偏航角曲线
3)助推火箭推力偏心计算
分别取无人机助推火箭推力偏心3′,6′,9′工况,对其在0.5 s发射阶段进行动力学仿真,得出无人机发射过程中的位移和角度随时间的变化规律。仿真结果表明:随着无人机助推火箭推力偏心角度的增大,无人机质心X、Y向位移的变化不明显,Z向的位移偏移量随之增加;俯仰角的变化不明显,滚转角和偏航角的偏移量也随之增加。若推力偏心角度较大,导致滚转角和偏航角偏移量过大,不利于无人机的稳定发射,因此,在研制设计时需要控制助推火箭推力的偏心角度。
Z向位移、滚转角和偏航角的变化规律如图7~图9所示。
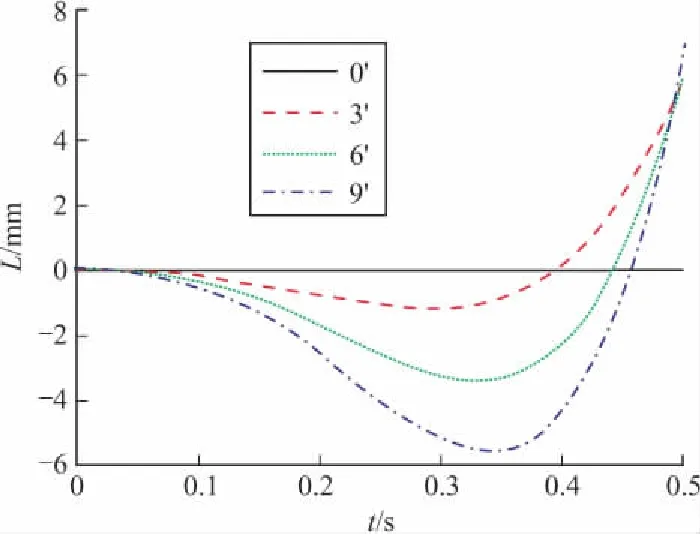
图7 无人机质心Z向位移曲线
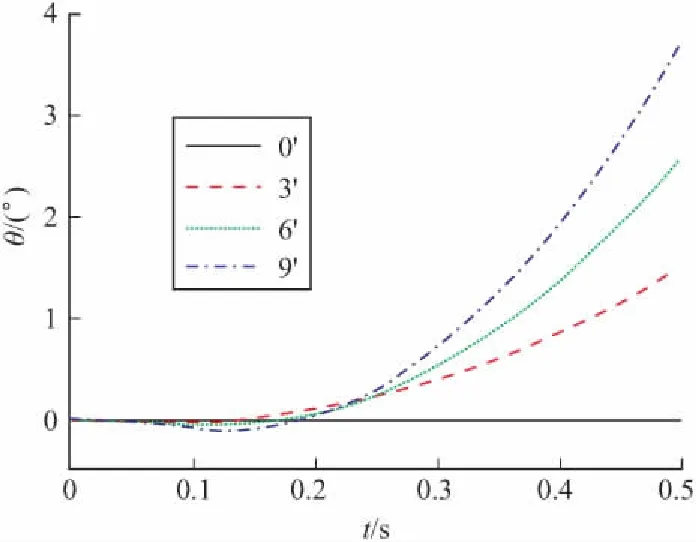
图8 无人机质心X向滚转角度曲线
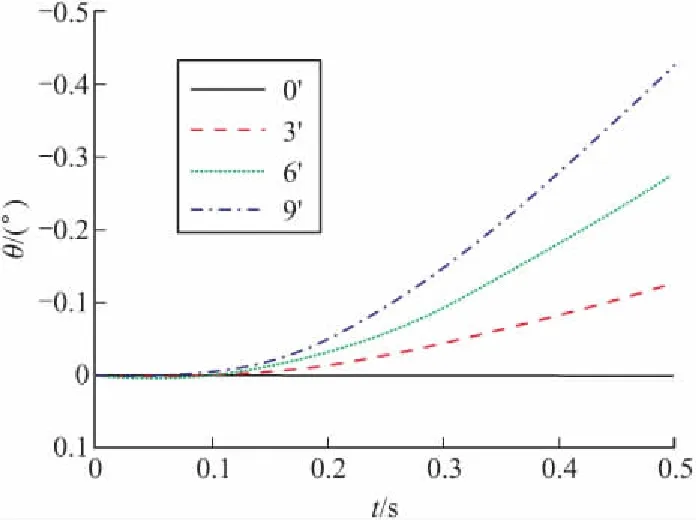
图9 无人机质心Y向偏航角度曲线
3.2 发射安全距离分析
无人机发射初始阶段,无人机助推器与发射架距离存在一定风险,助推火箭与发射架可能发生干涉的位置如图10所示。
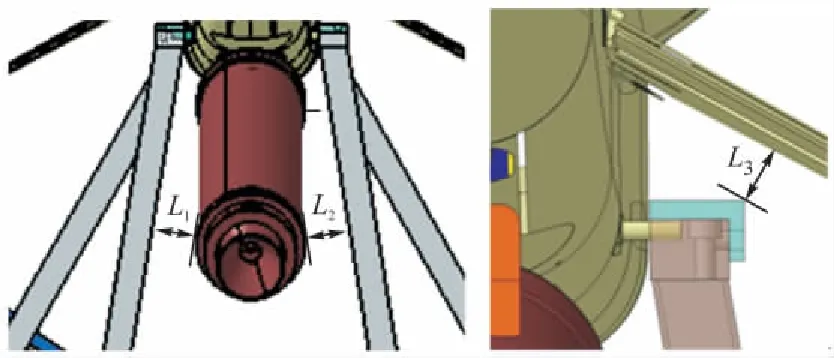
图10 无人机与发射架距离较短位置
由仿真结果可得:各工况下,无人机在0.203s时刻,助推火箭后端到后支撑侧向的距离L1和L2达到最小值;无人机在0.129 2s时刻,尾翼到导轨的距离L3达到最小值,间距如表1所示。
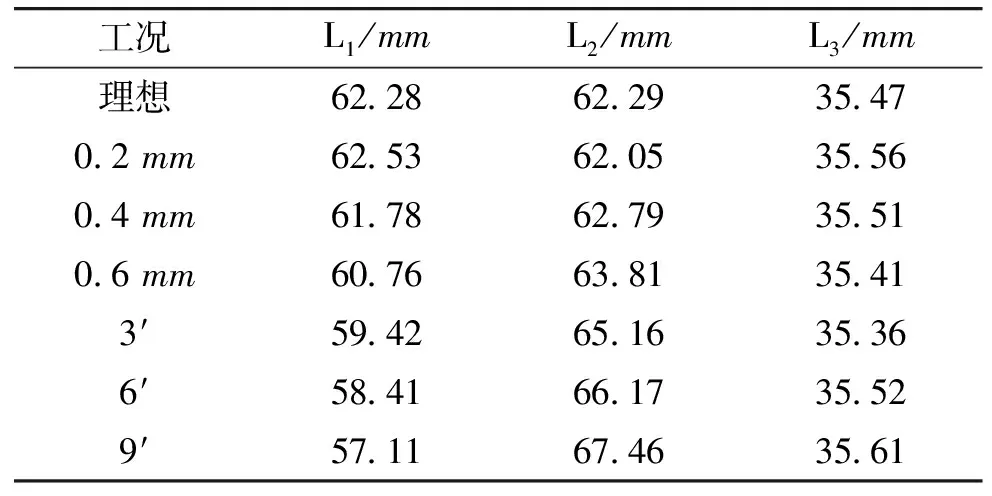
表1 助推火箭与发射架间距
表1表明,在质心和火箭推力偏心工况下,随侧向偏移量增大,助推火箭到侧支架的距离L1和L2之间的偏差越来越大;在质心偏心0.6mm工况下偏移量为3.05mm,在推力偏心9′工况下,偏移量达到了10.35mm;尾翼到导轨的距离L3变化不明显,偏移值在设计值范围内,满足发射安全性要求。无人机与发射架之间的距离L1、L2和L3均大于最小安全设计值,因此无人机在发射过程中能够安全离开发射架,不会发生干涉。
4 结论
仿真结果表明:无人机质心偏心和助推火箭推力偏心对无人机位移和角度有一定的影响,且推力偏心的影响更明显,因此在无人机系统研制过程中,质心和推力偏心均不能过大,控制助推火箭与无人机的安装精度尤为重要;根据发射安全距离分析可知:无人机与发射架不会发射干涉,最小安全距离也满足零长发射要求。
[1] 盛怀洁.无人机发射回收方式面面观 [J].无人机,2004(3):42-44.
[2] 余勇.无人机是如何起飞和回收的 [J].兵工科技,2006(10):60-61.
[3] 马威,过海峰,姜宁.海军通用无人机及其起降方式分析 [J].飞航导弹,2006(12):37-40.
[4] 张胜三,顾银芳.倾斜零长发射技术研究 [J].导弹与航天运载技术,2009(6):41-45.
[5] 廖莎莎,吴成.机载导弹发射动力学建模与虚拟样机仿真 [J].北京理工大学学报,2011,31(9):1013-1017.
SimulationandAnalysisofUAVZero-lengthLaunchingDynamicsBasedonADAMS
SHI Lin,MA Wei,YANG Longjun
(Jiangxi Hongdu Aviation Industry Group Corporation Limited,Nanchang 330024,China)
According to the requirement of UAV zero-length launching system development,the launch section of UAV zero-length lauching was taken as the main research object,and Adams was used to establish UAV launching dynamics simulation model.The dynamic simulation of centroid eccentricity and the thrust eccentric condition of booster rocket was carried out,and the centroid displacement and the angle change law of UAV in launching process were obtained.And the safety distance between the UAV and launcher was analyzed.The results showed that the centroid eccentricity and thrust eccentricity affected the motion attitude of UAV,and the influence of thrust eccentricity was more obvious.The UAV could safely leave the launcher during launching.
UAV; zero-length launching; simulation; model
10.15892/j.cnki.djzdxb.2017.02.009
2016-05-05
石林(1980-),男,江西鄱阳人,高级工程师,研究方向:发射、机械、液压、仿真。
V553
A
