铁基超导体中非磁性杂质引起的隙内束缚态

刘志海, 刘江山, 马建明, 郑铁军, 张德刚

(1. 四川师范大学 物理与电子工程学院, 四川 成都 610101; 2. 成都纺织高等专科学校 基础部, 四川 成都 611731)

铁基超导体中非磁性杂质引起的隙内束缚态

刘志海1, 刘江山1, 马建明1, 郑铁军2, 张德刚

(1. 四川师范大学 物理与电子工程学院, 四川 成都 610101; 2. 成都纺织高等专科学校 基础部, 四川 成都 611731)

铁基超导体中单个非磁性杂质引起的隙内束缚态可以用来区分S-波和S±-波配对对称性.基于一个两轨道四带紧束缚模型,研究在具有S±-波配对对称性的铁基超导体中单个非磁性杂质对局域态密度的影响,获得杂质共振峰的高度、位置与杂质势的关系.发现在一定的杂质势范围内正、负能侧杂质共振峰出现的位置是对称的,当VS>0.40 eV时,正能侧的共振峰分裂为2个峰,VS=0.70 eV附近区间,在次近邻点上的局域态密度中可以观察到4个明显的杂质共振峰,分别位于ω±3.4 meV和ω±2.2 meV处，像这样的隙内束缚态可以通过扫描遂穿实验直接观测.

铁基超导体; 超导序参量; 非磁性杂质; 隙内束缚态

新型超导材料铁基超导体的发现[1-5],为高温超导电性的研究提供了新的平台.到目前为止,已获得的铁基超导材料的最高转变温度高达55 K[2].与铜氧化物超导体类似,铁基超导体也有一个层状结构,超导电性来自于FeAs层中的电子库伯对.与铜氧超导体不同的是,铁基超导体中每个Fe原子位于相邻的4个As原子组成的四面体的中心,每个元胞中的2个As原子分别位于Fe-Fe平面上方和下方.能带计算[6-7]和ARPES实验[8-12]已经揭示铁基超导体中存在围绕Γ(0,0)点的2个空穴型费米面和围绕M(π,π)点的2个电子型费米面.

在铁基超导电性的研究中,超导序参量的配对对称性一直是一个核心的问题.大量的理论研究[13-17]以及通过STM实验描绘的Fe(Te,Se)材料中准粒子干扰模式与磁场的关系[18]都表明,铁基超导体中电子型费米面和空穴型费米面上的超导序参量带有相反的符号.众多实验[19-23]也揭示了各个费米面上的超导能隙是无节点的、接近各向同性的,因此d-波及p-波配对可以被排除.所以一般认为铁基超导体中的超导序参量为具有带间符号反转的S±-波配对,但也有研究[24-25]认为其超导序参量可能为S++-波配对,即各向异性的S-波配对.相对于d-波及p-波配对,S-波和S±-波配对更难以区分,因为除了沿着M点的2个费米面上的超导序参量反号外,二者具有相似的对称性.

众所周知,杂质的研究是高温超导电性研究的一个重要手段[26].在铁基超导体的超导序参量的研究中,非磁性杂质散射会在S±-波配对对称性中引起隙内束缚态,而这样的束缚态不会出现在S-波配对对称性中[27-29],通过STM实验描绘铁基超导体中杂质点及其邻近点上的局域态密度可以直接地观测非磁性杂质引起的隙内束缚态.铁基超导体中单个非磁性杂质引起的隙内束缚态可以作为S±-波配对对称性存在的信号.

本文的研究将基于一个两轨道四带紧束缚模型[27].该模型充分考虑了Fe-Fe平面上、下方配体As原子对该平面内电子态的影响,对于研究铁基超导材料晶体裂开的表面层或表面敏感实验中的层是十分必要的.该模型不仅成功地解释了STM实验所观察到的间隙铁杂质引起的零能束缚态[30]、畴壁结构[31-32],重复了核磁共振以及中子散射实验获得的超导相图[33-34],也成功地解释了STM实验观察到的涡流核中的负能共振峰[35-36].本文将基于该理论模型,通过调节非磁性杂质势的大小,研究铁基超导体中单个非磁性杂质引起的隙内束缚态.

1 理论模型

在两轨道四带紧束缚模型中,考虑了每个元胞中包含2个Fe原子和2个As原子,每个Fe原子包含2个简并轨道dxz、dyz.因为与Fe原子相邻的4个As原子有2种不同的排列方式,所以可将其晶格划分为亚晶格A和亚晶格B,每个亚晶格中包含一种Fe(A或B)原子和一种As(A或B)原子,As原子位于Fe-Fe平面上方(A)或下方(B).

两轨道四带紧束缚模型的哈密尔顿量为

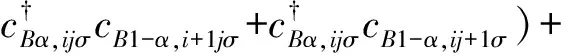
(1)

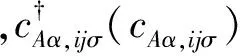
利用傅里叶变换式

将实空间的哈密尔顿量变换到动量空间并化简得

(2)

作参数替换

(3)

并将H0写成矩阵形式,可得到如下方程

(4)

由于波函数不为零,解方程可得

(5)

解得的对应本征函数为

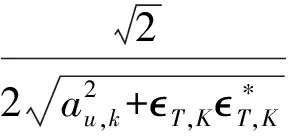
(6)

其中,下脚标0、1分别代表简并轨道dxz、dyz,u(ν)=0、1代表不同的能带,晶格常数取a=1.

为了将哈密尔顿量H0对角化,作如下正则变换

(7)

最终得到哈密尔顿量H0的如下对角形式

(8)

其中

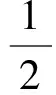
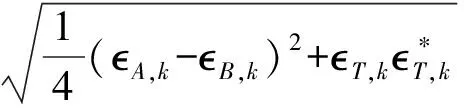
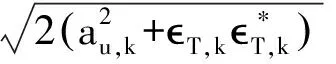
为了探究铁基超导体的超导电性,引入平均场BCS哈密尔顿量

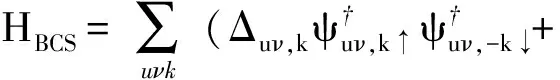
(9)

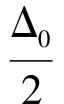
H=H0+HBCS+HNMI,

(10)

作波戈留波夫变换,令

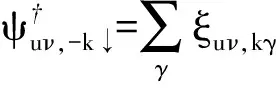
(11)

可将总的哈密尔顿量H对角化得

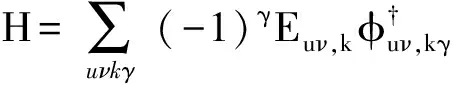
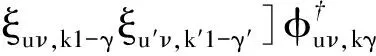
(12)

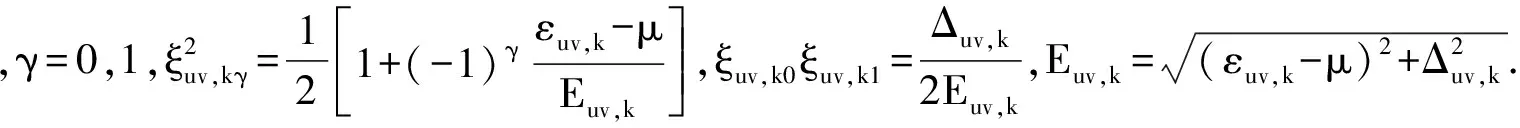
为了解出局域态密度的表达式,构造格林函数

(13)

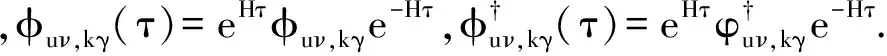
求解可得

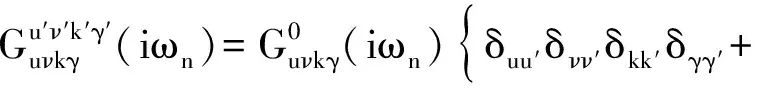
(14)

两轨道四带紧束缚模型中亚晶格A、B上的局域态密度分别为:

(15)

(16)

式中

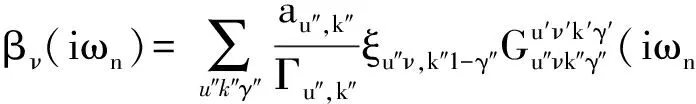
在本文的计算中,采用文献[27]中给出的参数,取Δ05.8meV,t1=0.5,t2=0.2,t3=-1.0,t4=0.02,μ=-0.49eV对应于理想电子掺杂(15%).

2 非磁性杂质引起的隙内束缚态

图1中描述的是根据 (15)和(16) 式计算得到的无杂质时(Vs=0)亚晶格A和B原点处的局域态密度,可以明显地观察到无杂质时亚晶格A、B原点处的局域态密度曲线基本重合.存在一大一小2个能隙Δ=5.8meV,Δ2=4.8meV,这与铁基超导体的多费米面结构有关,较小能隙来自于β费米面[19-20],该计算结果与S.Grothe等[37]通过STM实验观测到的结果吻合.

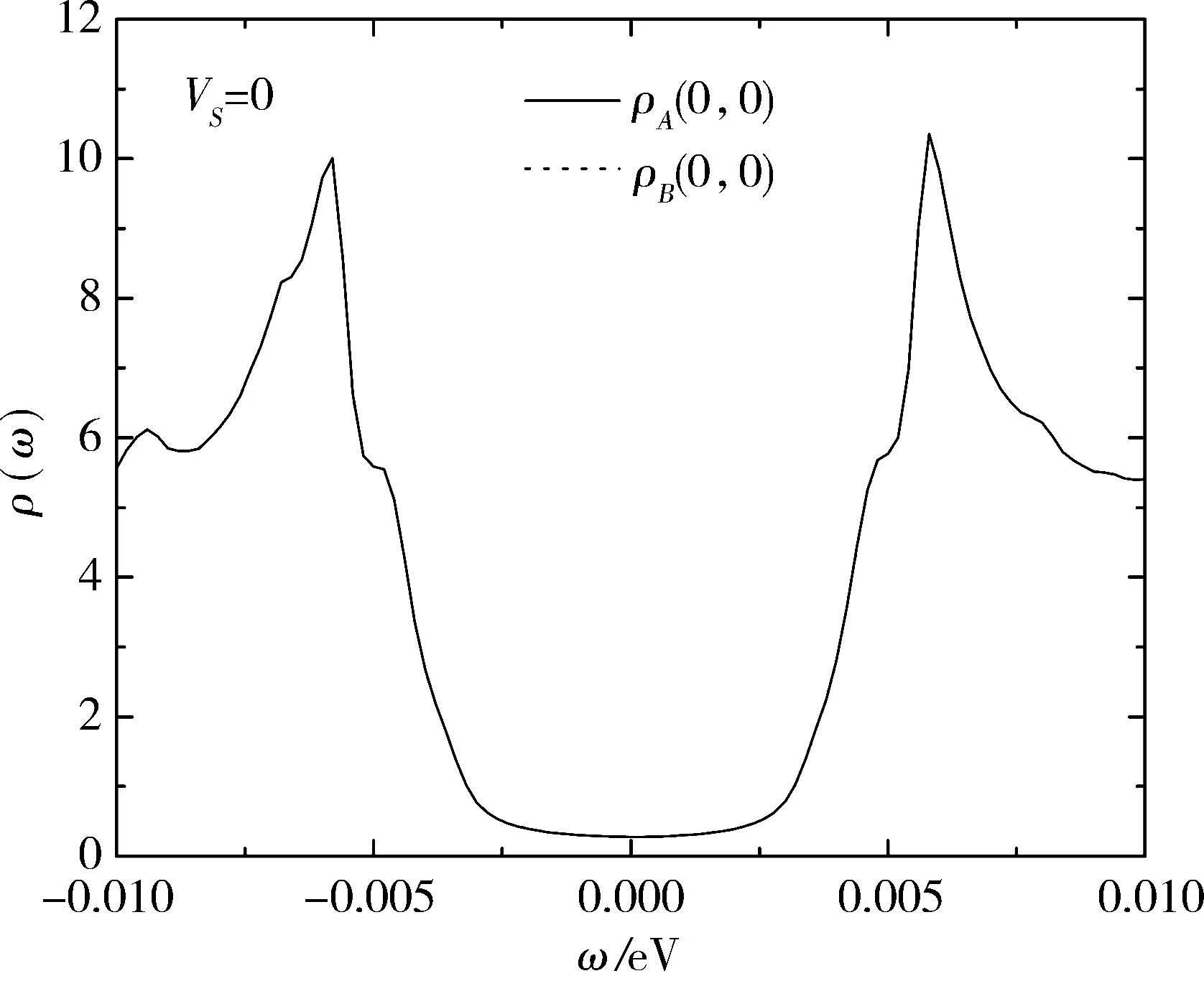
图 1 无杂质时亚晶格A、B原点处的局域态密度

下面计算一个位于亚晶格A原点处的单个非磁性杂质对局域态密度的影响.图2为杂质势(VS>0,排斥势)取不同值时在杂质点、最近邻点以及次近邻点上的局域态密度.在杂质点上,当VS=0.13 eV时,仅能在ω-3.4 meV处观察到明显的杂质共振峰.随着VS的增大,在正能侧对称的位置也出现共振峰;当VS=0.22 eV时杂质共振峰分别出现在ω±2.8 meV处,正、负能侧共振峰高度的变化趋势均为先增大然后逐渐减小;当VS<0.40 eV时,两侧峰的位置都逐渐向零能移动;VS<0.80 eV时,较高的峰均出现在负能侧.

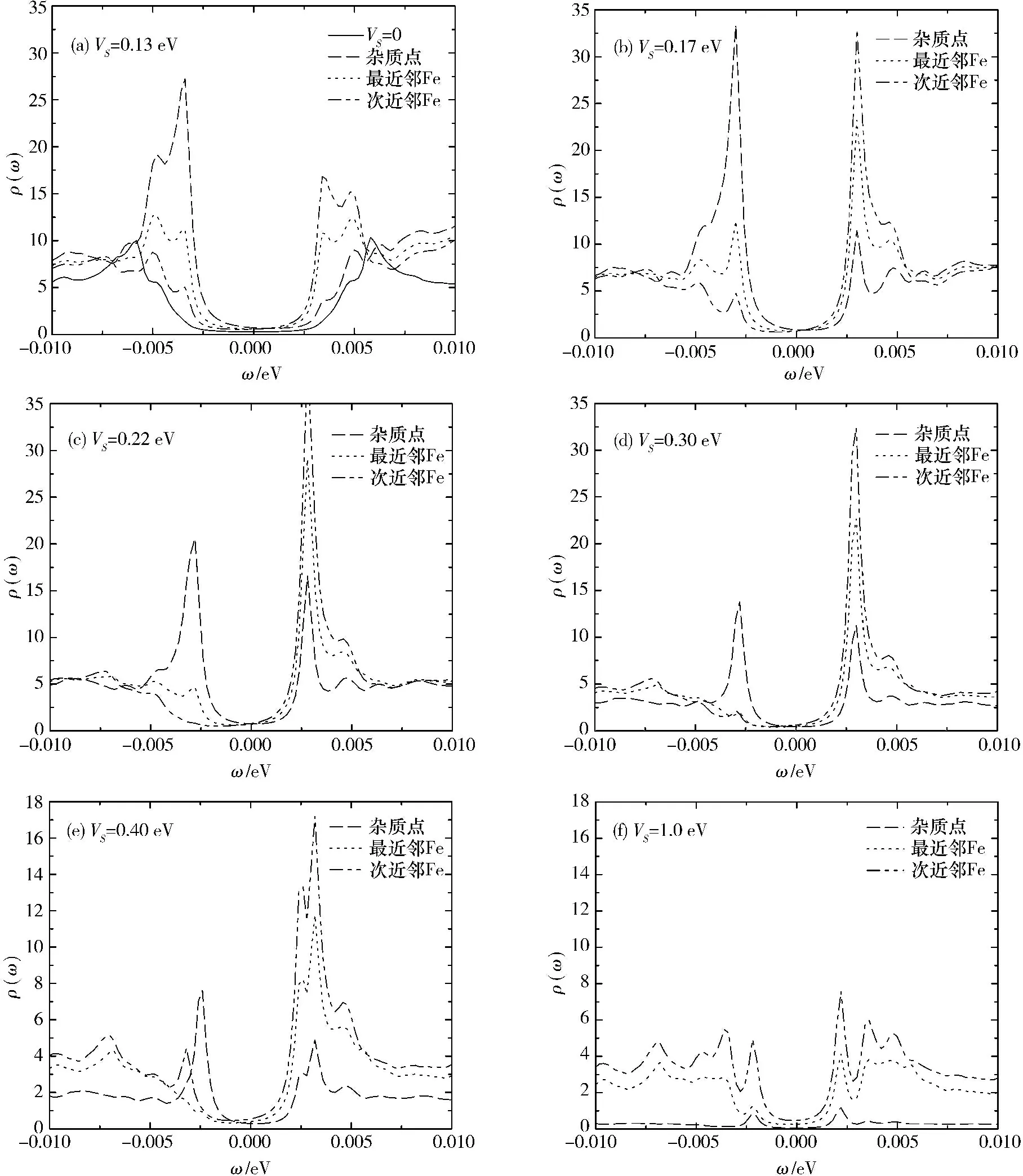
图 2 排斥势(VS>0)时杂质点、最近邻点、次近邻点上的局域态密度

在最近邻点上,当VS=0.13 eV时,可以观察到2个杂质共振峰,分别位于ω±3.4 meV处,随着VS的增大,共振峰高度的变化趋势与杂质点相同;VS<0.35 eV时,正、负能侧共振峰出现的位置也与杂质点相同,但较高的峰出现在正能侧,负能侧的峰较不明显;当VS在0.35 eV～1.0 eV范围内时,在负能侧观察不到明显的杂质共振峰.

在次近邻点上,当VS=0.13 eV时,也可在ω±3.4 meV处观察到2个杂质共振峰,但当VS在0.17 eV～0.30 eV范围内时负能侧的共振峰消失;VS>0.30 eV时在负能侧重新出现可观察到的杂质共振峰,但负能侧共振峰出现的位置与杂质点不再相同,如图2(e);当VS<1.0 eV时较高的峰均出现在正能侧.

随着VS继续增大,3个点上的局域态密度值都逐渐降低,当VS→+时,杂质点上的局域态密度趋于零.此外,在图2(e)中可以明显地观察到在杂质点、最近邻点以及次近邻点上的局域态密度中位于正能侧的杂质共振峰均分裂为2个峰.

为了详细地研究图2(e)中正能侧共振峰的分裂,分析了VS>0.40 eV时3个点上的局域态密度的变化情况,随着VS的增大,正能侧2个共振峰的绝对高度都在降低,但靠近零能的峰相对于靠近能隙边缘的峰变得更高;VS<1.0 eV时靠近零能的峰逐渐向零能移动,靠近能隙边缘的峰则逐渐向能隙边缘移动.图3给出了VS=0.70 eV时在杂质点、最近邻点以及次近邻点上的局域态密度.在次近邻点上,可以明显地观察到在ω±3.4 meV和ω±2.2 meV处共存在4个杂质共振峰.在最近邻点上,可以观察到2个杂质共振峰分别位于ω+3.4 meV和ω+2.2 meV处,虽然在ω-3.4 meV和ω-2.2 meV处观察不到明显的共振峰,但经过对数据仔细地分析可以发现,在最近邻点上的局域态密度中在上述2点都存在极大值.在杂质点上,在ω±2.2 meV和ω+3.4 meV处共可观察到3个杂质共振峰,同样分析数据可以发现,在杂质点上的局域态密度中在ω-3.4 meV处也存在极大值.

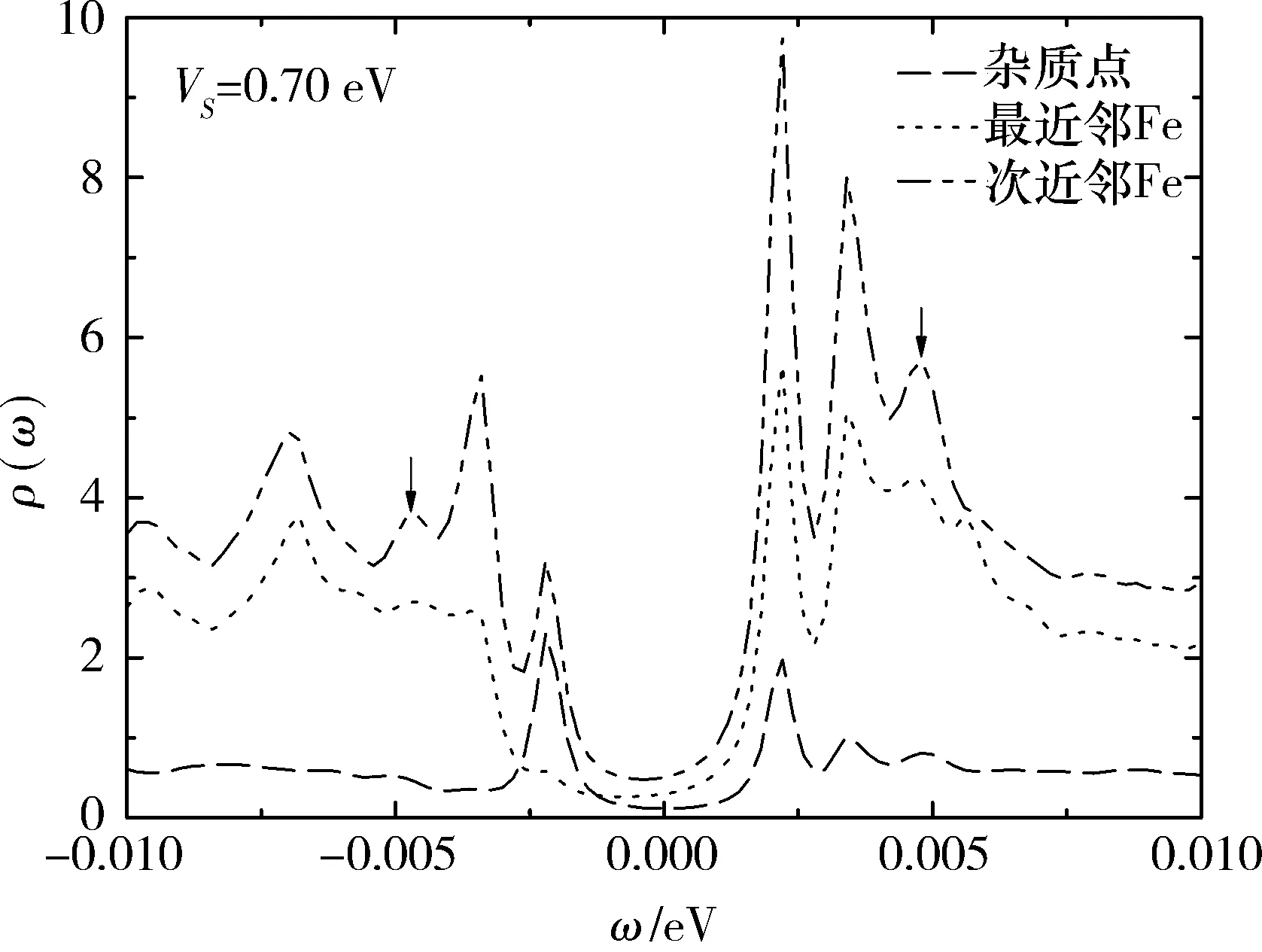
图 3 VS=0.70 eV时杂质点、最近邻点、次近邻点上的局域态密度

注：箭头代表较小能隙(Δ2=4.8 meV)的相干峰

图4中描述的是杂质势为吸引势(VS<0)时的情况.在杂质点上,当VS=-0.13 eV时,仅能在ω+4.2 meV处观察到一个杂质共振峰.随着|VS|的增大,峰的位置逐渐向零能移动,局域态密度值逐渐减小并趋于零,在负能侧始终没有共振峰出现.在最近邻点上,|VS|<1.0 eV时,在正、负能侧均观察不到明显的杂质共振峰,当VS=-1.0 eV时,其局域态密度中存在一个共振峰,位于ω-2.8 meV处.在次近邻点上,当VS=-0.13 eV时,可以在ω-4.2 meV处观察到一个杂质共振峰,共振峰的位置随|VS|的变化趋势与杂质点相同,当VS=-1.0 eV时,其局域态密度中存在2个共振峰,分别出现在ω-3.8 meV和ω-2.8 meV处.3个点上的局域态密度值都随着|VS|的增大而减小,当VS→-时,杂质点上的局域态密度趋于零.

图2(a)和4(a)中都给出了VS=0时的局域态密度,通过对比可以明显地看出,与排斥势相比,吸引势时杂质共振峰的高度更低、峰出现的位置更加靠近能隙边缘,吸引势对局域态密度有较小的影响.当VS>0.13 eV时,局域态密度中较小能隙Δ2依然能够被清晰地观察到,但较大能隙Δ的相干峰则完全消失,如图2,非磁性杂质对较大能隙Δ有较强的抑制作用.当|VS|<0.11 eV时,无论对于排斥势还是吸引势,在3个点上的局域态密度中均未观察到明显的隙内束缚态.

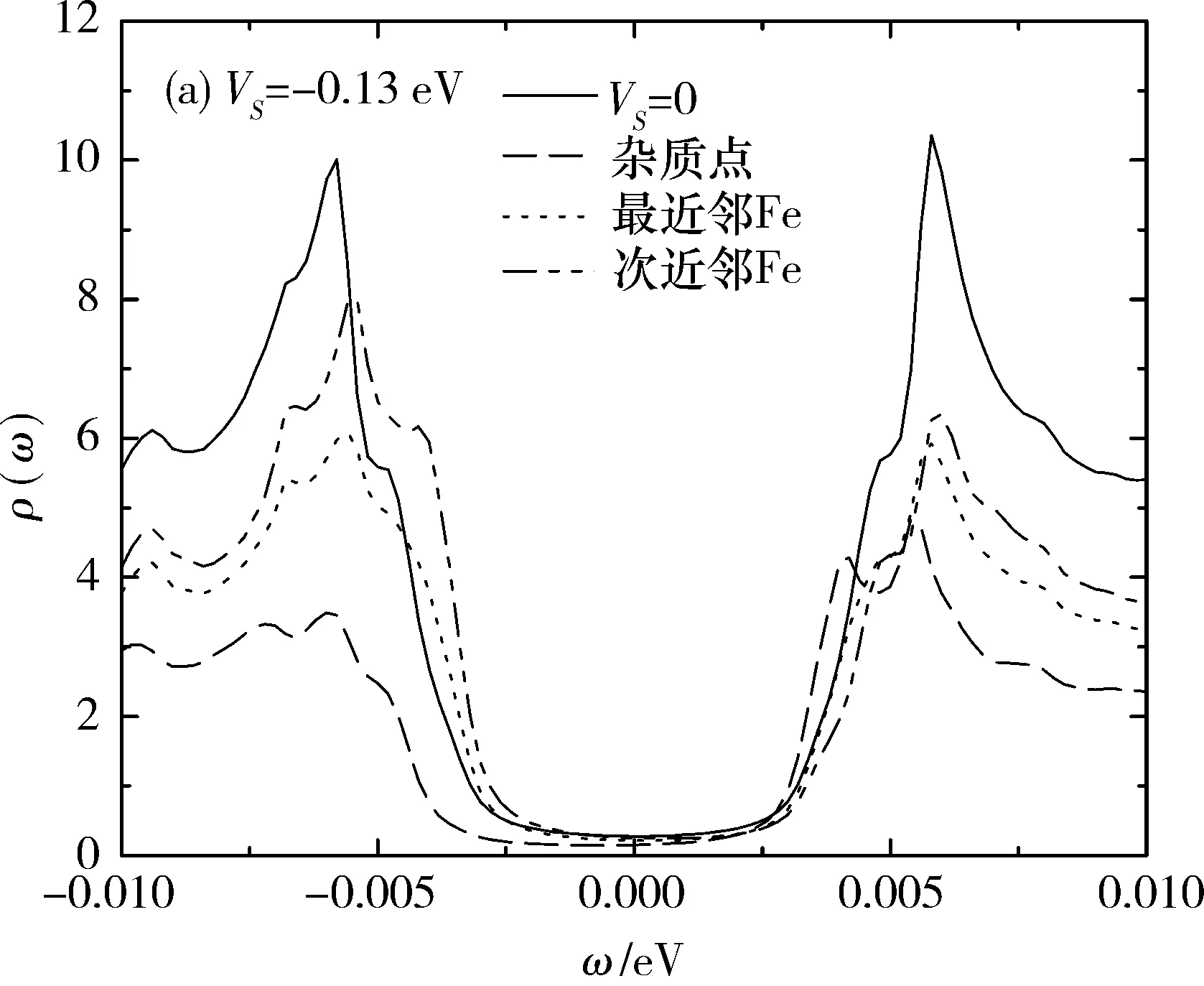
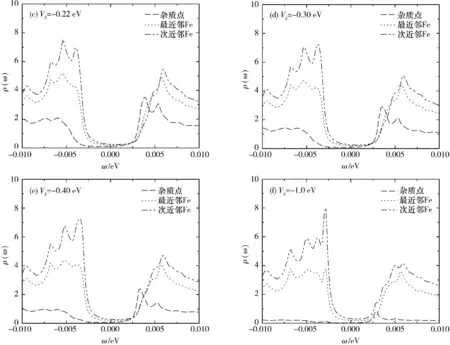
图 4 吸引势(VS<0)时杂质点、最近邻点、次近邻点上的局域态密度

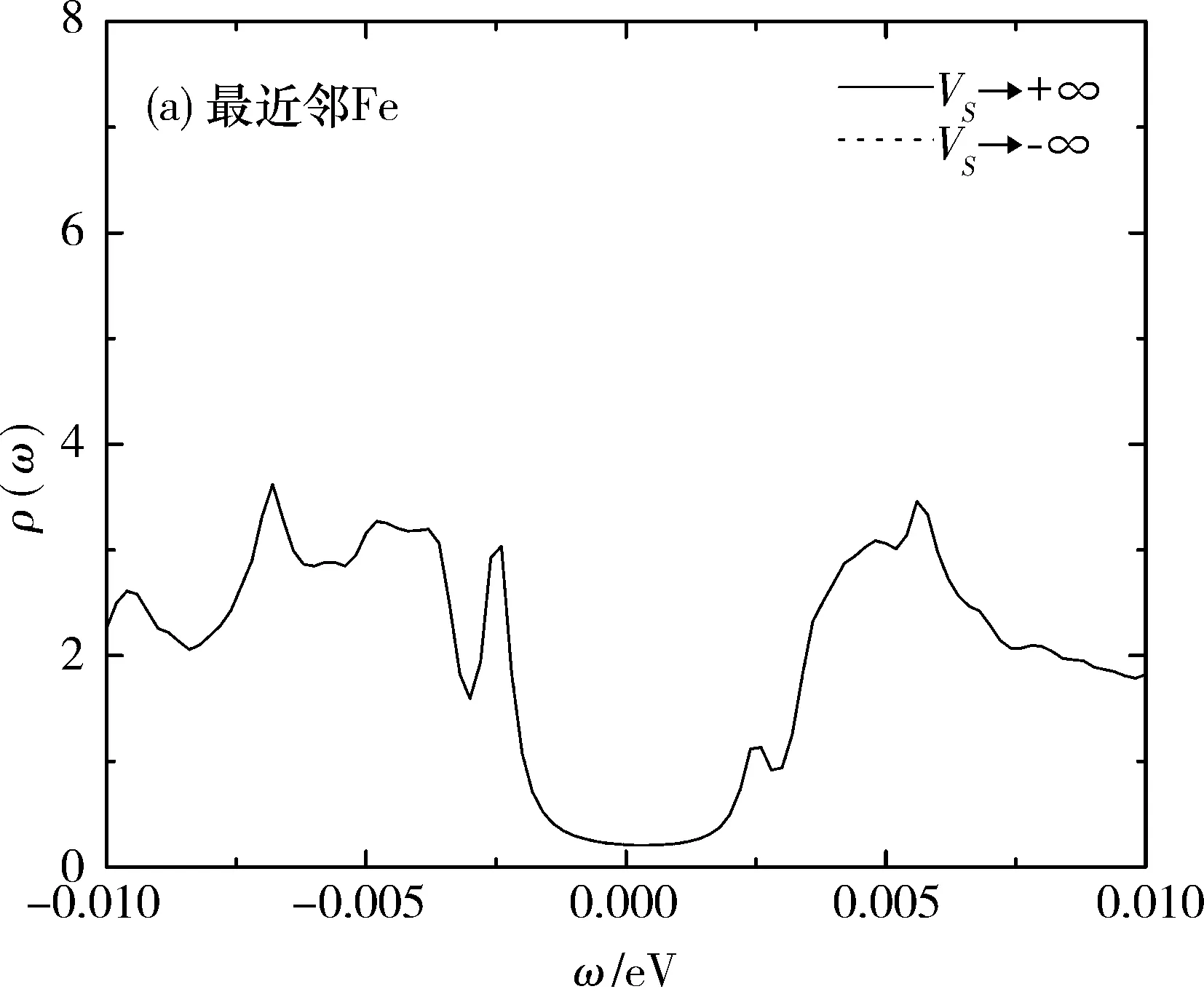
我们也计算了杂质势取幺正极限(VS→)时的情况,如图5所示.当VS→时,杂质点上的局域态密度趋于零,最近邻点和次近邻点上的局域态密度的变化趋势相同,较高的峰都出现在负能侧,但次近邻点上的共振峰高度更高.当VS→+和VS→-时,最近邻点和次近邻点上的局域态密度曲线分别重合.在次近邻点上的局域态密度中可以明显地观察到4个杂质共振峰,分别位于ω±3.6 meV和ω±2.4 meV处.

3 结果与讨论

本文基于一个铁基超导体的两轨道四带紧束缚模型,详细地研究了在具有S±-波配对对称性的铁基超导体中一个位于亚晶格A原点处的非磁性杂质对局域态密度的影响.通过调节非磁性杂质势VS的大小,详细地分析了在不同杂质势下单个非磁性杂质引起的隙内束缚态,获得了杂质共振峰的高度及位置随杂质势VS的变化规律,与Kariyado等[28]基于一个五轨道模型研究得出的变化规律定性一致.我们也计算了杂质势取幺正极限时的情况,当VS→时,杂质点上的局域态密度趋于零,在最近邻点和次近邻点上的局域态密度中在靠近能隙边缘处可以观察到明显的隙内束缚态.本文中发现当杂质势在一定范围内时,正、负能侧杂质共振峰出现的位置是对称的,当VS>0.40 eV时,正能侧的杂质共振峰分裂为2个峰,在VS=0.70 eV附近区间,在次近邻点上的局域态密度中可以观察到4个杂质共振峰,分别位于ω±3.4 meV和ω±2.2 meV处.铁基超导体中单个非磁性杂质引起的隙内束缚态可以用来区分其超导序参量的S-波和S±-波配对对称性,而这样的隙内束缚态能够通过STM/STS实验描绘的杂质点及其邻近点上的局域态密度图像直接观测.

[1] KAMIHARA Y, WATANABE T, HIRANO M, et al. Iron-based layered superconductor La [O1-xFx] FeAs (x=0.05-0.12) with Tc= 26 K[J]. Am Chem Soc,2008,130(11):3296-3297.

[2] ZHI A R, WEI L, JIE Y, et al. Superconductivity at 55 K in iron-based F-doped layered quaternary compound Sm [O1-xFx] FeAs[J]. Chin Phys Lett,2008,25(6):2215.

[3] CHEN X H, WU T, WU G, et al. Superconductivity at 43 K in SmFeAsO1-xFx[J]. Nature,2008,453(7196):761-762.

[4] CHEN G F, LI Z, WU D, et al. Superconductivity at 41 K and its competition with spin-density-wave instability in layered CeO1-xFxFeAs[J]. Phys Rev Lett,2008,100(24):247002.

[5] WEN H H, MU G, FANG L, et al. Superconductivity at 25 K in hole-doped (La1-xSrx) OFeAs[J]. Euro phys Lett,2008,82(1):17009.

[6] SINGN D J, DU M H. Density functional study of LaFeAsO1-xFx:a low carrier density superconductor near itinerant magnetism[J]. Phys Rev Lett,2008,100(23):237003.

[7] NEKRASOV I A, PCHELKINA Z V, SADOVSKII M V. Electronic structure of prototype AFe2As2and ReOFeAs high-temperature superconductors:a comparison[J]. JETP Lett,2008,88(2):144-149.

[8] LU D H, YI M, MO S K, et al. Electronic structure of the iron-based superconductor LaOFeP[J]. Nature,2008,455(7209):81-84.

[9] LIU C, SAMOLYUK G D, LEE Y, et al. K-doping dependence of the Fermi surface of the iron-arsenic Ba1-xKxFe2As2superconductor using angle-resolved photoemission spectroscopy[J]. Phys Rev Lett,2008,101(17):177005.

[10] ZABOLOTNYY V B, INOSOV D S, EVTUSHINSKY D V, et al. (π,π) Electronic order in iron arsenide superconductors[J]. Nature,2009,457(7229):569-72.

[11] TERASHIMA K, SEKIBA Y, BOWEN J H, et al. Fermi surface nesting induced strong pairing in iron-based superconductors[J]. Proceedings of the National Academy of Sciences,2009,106(18):7330-7333.

[12] SEKIBA Y, SATO T, NAKAYAMA K, et al. Electronic structure of heavily electron-doped BaFe1.7Co0.3As2studied by angle-resolved photoemission[J].New Physics,2009,11(2):025020.

[13] KUROKI K, ONARI S, ARITA R, et al. Unconventional pairing originating from the disconnected Fermi surfaces of superconducting LaFeAsO1-xFx[J]. Phys Rev Lett,2008,101(8):087004.

[14] MAZIN I I, SINGH D J, JOHANNES M D, et al. Unconventional superconductivity with a sign reversal in the order parameter of LaFeAsO1-xFx[J]. Phys Rev Lett,2008,101(5):057003.

[15] TSAI W F, YAO D X, BERNEVIG B A, et al. Properties of Josephson junctions involving the cos(kx)·cos(ky) pairing state in iron pnictides[J]. Phys Rev,2009,B80(1):012511.

[16] NOMURA T. Perturbation theory of high-Tc superconductivity in iron pnictides[J].Physical Society of Japan,2009,78(3):034716.

[17] GHAEMI P, WANG F, VISHWANATH A. Andreev bound states as a phase-sensitive probe of the pairing symmetry of the iron pnictide superconductors[J]. Phys Rev Lett,2009,102(15):157002.

[18] HANAGURI T, NIITAKA S, KUROKI K, et al. Unconventional s-wave superconductivity in Fe (Se,Te)[J]. Science,2010,328(5977):474-476.

[19] DING H, RICHARD P, NAKAYAMA K, et al. Observation of Fermi-surface-dependent nodeless superconducting gaps in Ba0.6K0.4Fe2As2[J]. Euro Phys Lett,2008,83(4):47001.

[20] NAKAYAMA K, SATO T, RICHARD P, et al. Superconducting gap symmetry of Ba0.6K0.4Fe2As2studied by angle-resolved photoemission spectroscopy[J]. Euro Phys Lett,2009,85(6):67002.

[21] HASHIMOTO K, SHIBAUCHI T, KATO T, et al. Microwave penetration depth and quasiparticle conductivity of PrFeAsO1-ysingle crystals:evidence for a full-gap superconductor[J]. Phys Rev Lett,2009,102(1):017002.

[22] EVTUSHINSKY D V, INOSOV D S, ZZBOLOTNYY V B, et al. Momentum dependence of the superconducting gap in Ba1-xKxFe2As2[J]. Phys Rev,2009,B79(5):054517.

[23] WANG X P, QIAN T, RICHARD P, et al. Strong nodeless pairing on separate electron Fermi surface sheets in (Tl,K) Fe1.78Se2probed by ARPES[J]. Euro Phys Lett,2011,93(5):57001.

[24] KONDO T, SANTANDER-SYRO A F, COPIE O, et al. Momentum dependence of the superconducting gap in NdFeAsO0.9F0.1single crystals measured by angle resolved photoemission spectroscopy[J]. Phys Rev Lett,2008,101(14):147003.

[25] KONTANI H, ONARI S. Orbital-fluctuation-mediated superconductivity in iron pnictides: analysis of the five-orbital Hubbard-Holstein model[J]. Phys Rev Lett,2010,104(15):157001.

[26] BALATSKY A V, VEKHTER I, ZHU J X. Impurity-induced states in conventional and unconventional superconductors[J]. Reviews of Modern Physics,2006,78(2):373.

[27] ZHANG D. Nonmagnetic impurity resonances as a signature of sign-reversal pairing in FeAs-based superconductors[J]. Phys Rev Lett,2009,103(18):186402.

[28] KARIYADO T, OGATA M. Single-impurity problem in iron-pnictide superconductors[J]. J Phys Society Jpn,2010,79(8):1154-1174.

[29] TSAI W F, ZHANG Y Y, FANG C, et al. Impurity-induced bound states in iron-based superconductors with s-wave coskx·coskypairing symmetry[J]. Phys Rev,2009,B80(6):064513.

[30] ZHANG D. In-gap bound states induced by interstitial Fe impurities in iron-based superconductors[J]. Physica C:Superconductivity and Its Applications,2015,519:43-46.

[31] HUANG H, ZHANG D, ZHOU T, et al. Domain walls in normal and superconducting states of iron pnictides[J]. Phys Rev,2011,B83(13):134517.

[32] LI B, LI J, BASSLER K E, et al. Magnetic domain walls induced by twin boundaries in low doped Fe-pnictides[J].New Physics,2013,15(10):103018.

[33] LAPLACE Y, BOBROFF J, RULLIER-ALBENQUE F, et al. Atomic coexistence of superconductivity and incommensurate magnetic order in the pnictide Ba (Fe1-xCox) 2As2[J]. Phys Rev,2009,B80(14):140501.

[34] ZHOU T, ZHANG D, TING C S. Spin-density wave and asymmetry of coherence peaks in iron pnictide superconductors from a two-orbital model[J]. Phys Rev,2010,B81(5):052506.

[35] GAO Y, HUANG H X, CHEN C, et al. Model of vortex states in hole-doped iron-pnictide superconductors[J]. Phys Rev Lett,2011,106(2):027004.

[36] SHAN L, WANG Y L, SHEN B, et al. Observation of ordered vortices with Andreev bound states in Ba0.6K0.4Fe2As2[J]. Nature Physics,2011,7(4):325-331.

[37] GROTHE S, CHI S, DOSANJH P, et al. Bound states of defects in superconducting LiFeAs studied by scanning tunneling spectroscopy[J]. Phys Rev,2012,B86(17):174503.

In-gap Bound States Induced by a Nonmagnetic Impurity in Iron-based Superconductors

LIU Zhihai1, LIU Jiangshan1, MA Jianming1, ZHENG Tiejun2, ZHANG Degang1

(1.CollegeofPhysicsandElectronicEngineering,SichuanNormalUniversity,Chengdu610101,Sichuan;2.DepartmentofFundamentalEducation,ChengduTextileCollege,Chengdu611731,Sichuan)

In-gap bound states induced by a nonmagnetic impurity can be used to distinguish the S-wave and S±-wave pairing symmetry in iron-based superconductors. Based on a two-orbit four-band tight binding model, the effect of single nonmagnetic impurity effects on the local density of states in iron-based superconductors with the S±-wave symmetry is studied. The dependence of the intensities and positions of the impurity resonance peaks and the strength of impurity potential was obtained. The resonance peaks at positive and negative energies are symmetric in a certain range of the impurity potential. The impurity resonance peak at positive energy splits into two peaks whenVS>0.40 eV. An impurity withVS=0.70 eV induces four impurity resonance peaks on the next-nearest-neighbor site atω=±3.4 meV andω=2.2 meV, respectively. Such in-gap bound states could be observed by scanning tunneling microscopy experiments.

iron-based superconductors; superconducting order parameter; nonmagnetic impurity; in-gap bound states

2016-09-27

四川省“千人计划”资助项目(34125003)

*通信作者简介：张德刚(1962—)，男，教授，主要从事超导理论、自旋电子学和统计模型精确解的研究，E-mail：degangzhang@yahoo.com

O48

A

1001-8395(2017)05-0666-09

10.3969/j.issn.1001-8395.2017.05.018

(编辑 郑月蓉)