基于MFC的地势起伏度计算程序设计与实现
2017-11-07赵强
赵强


DOI:10.16660/j.cnki.1674-098X.2017.25.151
摘 要:地势起伏度是划分地貌类型的一项重要指标,提取地势起伏度的关键在于确定最佳分析区域窗口单元的选择,统计学上的均值变点法为目前最常用最有效的方法之一。其通常由人工计算法计算得出,该方法计算效率和准确度均较低。本文设计并实现一套基于MFC开发框架,结合STL模版类库的地势起伏度计算程序。选用青藏高原部分地势起伏度值为数据样本,实现均值变点法算法,通过实验,得到的结果准确且计算速度高,本程序将提高地势起伏度计算效率,得到广泛使用。
关键词:地势起伏度 均值变点法 MFC STL 程序设计
中图分类号:P20 文献标识码:A 文章编号:1674-098X(2017)09(a)-0151-05
Abstract: The relief degree is an important index of classification of geomorphologic types, The key to the extraction of topographic relief is to determine the optimal window unit of the analysis area. the Mean change-points method of statistics is one of the most commonly used and most effective methods. It is usually calculated by manual calculation. It has low computational efficiency and accuracy. In this paper, we design and implement a program based on MFC(MicroSoft Foundation Classes) development framework and STL(Standard template Library) Library. The part of the Qinghai-Tibetan Plateau is chosen as the data sample to realize the mean point change algorithm. Through experiment, The experiment results show that the results are accurate and the calculation speed is high. This program will improve the efficiency of relief calculation and widely used.
Key Words: Relief amplitude; Mean Change-Point method; MFC; STL; Programing
地势起伏度(Relief Amplitude)是指在所指定的分析区域内所有栅格中最大高程与最小高程的差,是反映地形起伏的宏观地形因子[1]。地势起伏度是划分地貌类型的一项重要指标。提取地势起伏度的关键在于确定最佳分析区域窗口单元的选择。利用DEM数据提取地势起伏度能够快速、直观地反映地形的起伏特征。本文以大尺度SRTM3-DEM为实验数据源,利用统计学上的均值变点法提取实验区地势起伏度并分级分析的算法,基于MFC编程框架以及STL模板类库实现基于研究区网格单元与平均地势起伏度对应关系计算均值变点分析结果的程序。经实验,本程序能够完全准确实现依据算法,计算准确度、速度均有提高。获得的结果可获得实验区域内地势起伏度最佳统计单元。
1 相关研究
针对不同地貌区域的地势起伏度计算已经有较多的研究,郑琴文、冯玉祥、王玲等在GIS系统的基础下,采用领域分析方法提取地势起伏度,运用均值变点分析法对其进行了最佳统计单元的计算[2-4];唐飞等基于DEM和TM影像利用ArcMap中邻域分析工具对准噶尔盆地及其西北山区地势起伏度进行研究最终确定了该地区地势起伏度计算的最佳统计单元[5];何文秀等运用地理信息系统窗口分析和统计分析等方法利用DEM数据研究了宁夏彭阳县的地势起伏度[6];赵斌滨等分析人工作图法与均值变点法是判断最佳统计单元相对有效的方法[7]。
MFC(Microsoft Foundation Class,微软基础类库)是微软公司为了简化程序员的开发工作所开发的一套C++类的集合,是一套面向对象的函数库,以类的方式提供给用户使用。可以用它来编写 Windows 应用程序。使用 MFC 类库和Visual C++提供的高度可视的应用程序开发工具,可使应用程序开发变得更简单,极大地缩短开发周期,提高代码的可靠性和可重用性[8,9]。
STL(Standard Template Library)标准模板库是C++标准规范的主要内容之一,其本身为几类“容器”的集合,其目的为构建标准化组件,以减少在编写应用程序过程中重复开发相同功能的代码,根据需要可以选择最优的数据结构组件实现高效的数据管理[10]。
2 变点分析法计算地势起伏度原理
本文试验数据选用基于SRTM3-DEM的数据青藏高原国内部分,其平面基准为WGS84,高程基准为EGM96,置信度达90%。对实验区的DEM数据进行拼接与投影转换处理。投影方式选择等面积圆锥投影,第一标准纬线定为25°N,第二标准纬线定为47°N,中央经线定為105°E,基准面选用Krasovsay_1940,将DEM栅格单元重采样为90m[11]。
应用窗口递增分析法来计算实验区中地势起伏度的最佳统计面积。分析窗口类型选择矩形,计算网格2×2、3×3、4×4、……32×32的地势起伏度,对计算得到的不同窗口下的地势起伏度,我们取各自的地势起伏度平均值(表1)然后与各单元窗口相对应的面积作对数拟合曲线。在面积从100~200之间出现曲线由陡变缓的点,而该点对应的面积即是我们寻找的最佳统计单元面积。endprint
利用均值变点法,计算出拟合曲线上由陡变缓的点位。基于变化网格大小区域的方法,计算出对应网格大小面积内平均地势起伏度值,将此平均地势起伏度值作为计算最佳统计面积的参考样本序列,对其对应的格网面积求单位面积上的平均地势起伏度,并求其自然对数构建原始样本序列。变点的存在使样本分段后的统计量Si的变化趋势会有一个转折。而该转折点处可以很直观得到网格半径大小,从而该网格半径所对应的区域面积即为最佳统计面积。
计算均值变点分析法计算过程如下[12]:
(1)令i=2,…,N,对每个i将样本分为两段:X1,X2,…,Xi-1和Xi,Xi+1,…,XN。
计算每段样本的自述平均值和及统计量。
(2)统计量:
和
(3)期望值:
(4)通过观察计算结果很容易就能得到统计结果趋势变化的点。
通过变点即可确定格网半径大小,从而确定最佳统计面积。
3 计算程序设计实现
利用输入样本数据,通过算法公式计算得出每段样本的前半段算术平均值和后半段算术平均值,以及输出统计量。基于MFC对话框程序构建,利用STL对数据进行管理。架构图如图1所示。
3.1 数据输入
由于样本数据量较小,可以选择手工输入或数据文件导入的形式,定义基于STL的map模板,第一个参数保存格网半径,即模版保存数据中的key数据,变量类型定义为整型值;第二个参数为不同格网大小范围内平均地势起伏度的平均值。数据从外部读入软件后,在内存中以map的形式组织保存。
3.2 数据预处理
单元格网面积相同,原始样本序列采用格网半径从2开始,依次递加1的方式取格网。随着格网半径的增加,样本格网的面积也在増加,而所取格网面积内的平均地势起伏度由于面积的増大,起伏度值也在増大。为了更好地找到拟合曲线上由陡变缓的这一临界点,我们需要对格网面积内再取单位网格面积的平均地势起伏度,并对其求自然对数来构建真正的原始样本序列。
所以在初始样本序列插入计算平均地势起伏度值的函数中,对平均地势起伏度值进行预处理,即定义原始样本构建函数:
selType CReliefDlg::insertReliefs(int num, double relief)
其中在构建计算用的平均地势起伏度原始样本序列ReliefMap中时,需要先进行平均格网地势起伏度的自然对数运算:
relief = log(relief / (num*num))
运算结果再插入原始样本序列中:
m_Reliefs.insert(make_pair(num, relief));
其中变量m_Reliefs为std::map
3.3 算法实现
由均值变点分析法,对样本序列进行计算时,需要设定一个起始i值,i值即为格网半径数变化序列,计算时将样本从当前i值处,分为前后两段样本,并且要对每段样本的算术平均值和分段样本的统计量。这也就相当于样本数量是动态变化的,而动态变化的数值需要通过函数参数传入计算过程。
由此,将求平均值的算法和求统计量的算法定义两个函数分别为:
double CReliefDlg::getAverValue(int iBeginPos, int iEndPos)
double CReliefDlg::getReliefS(int iBeginPos, int iEndPos)
通过输入样本序列的起始位置和终止位置来确定样本序列的内容和长度,而这一数值又同时与ReliefMap中第一个参数网格值相对应。故可以直接根据传参对样本序列Map进行遍历计算,得出当前动态样本序列的平均值和统计量;
在计算分段样本序列的基础上,对所有平均地势起伏度样本进行循环处理,依次计算当前样本递进时不同位置分段样本序列的统计量和算术平均值,并计算分段后的统计量Si的值,此值也正是我们需要求出并加以分析的结果。
3.4 程序实现
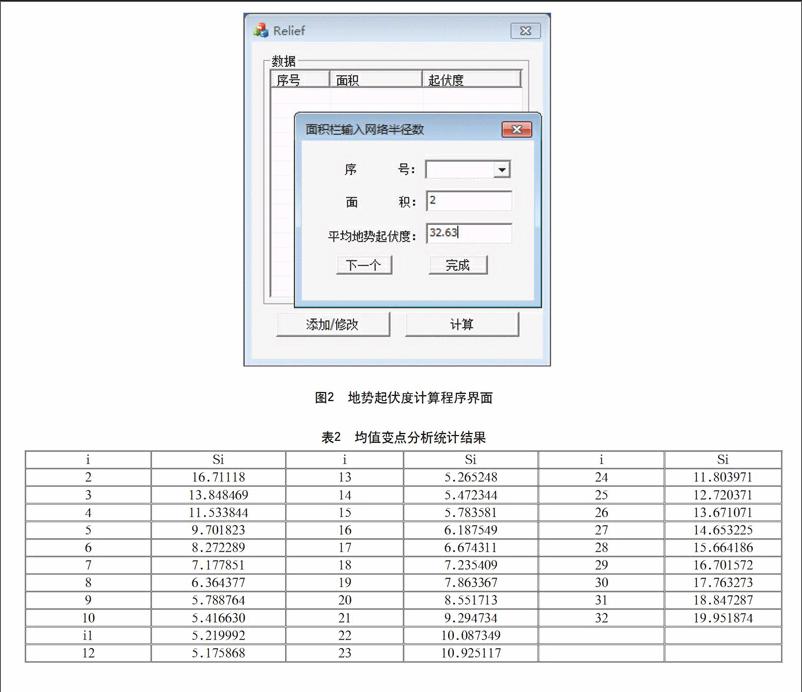
C++编程语言与MFC编程框架相结合,基于MFC可视化界面设计,程序主界面包含ListBox控件用于输入数据显示及修改、“添加/修改”按钮用于打开手动数据输入对话框以及启动起伏度值计算并输出计算结果的“计算”按钮,如图2。
手动数据输入对话框包含一个ComboBox下拉框控件,用于显示当前输入数值的序号,面积为EditBox,用于输入格网单元半径,平均地势起伏度即为对应网格大小区域内平均地势起伏度的值,一个数值输入完成,点击“下一个”即进行下一个地势起伏度值的输入,“完成”按钮即输入结束,手动数据输入对话框自动关闭,点击主界面“计算”按钮,计算Si值并输出到文本文档中。
3.5 结果输出
计算出Si值后,仍将其放入ReliefMap类型map模板数据结构中,利用STL中的map结构对其进行存储和管理,结果可以在主程序界面中的ListBox控件里插入显示,也可以文件形式输出保存到硬盘中。
4 数据验证
依据表1中的数值,输入程序后,计算可得均值變点分析的统计结果(表2)。
根据表2的分析计算结果可以很轻松得出均值变点分析结果曲线,如图3。
图中Si值为纵轴,i值为横轴,可以很清楚看出有一个很明显的趋势转折,格网半径i从2开始到12,其Si的值均为下降趋势;而格网半径i从12到31过程中,Si的值是呈上升趋势,即i=12这一点处即为我们的变点处,格网半径为12也即为要求的最佳统计单元格网半径,其对应的面积即为最佳统计面积,与实验预期结果一致。
5 结语
对地势起伏度计算中基于平均地势起伏度和变点分析法求最佳统计面积是地势起伏度研究中比较重要的研究方法之一。本文基于MFC利用模板庫STL对以上地势起伏度计算方法进行程序实现,并针对特定实验区数据计算,得到的结果与预期结果一致。本文设计实现的程序具有计算速度快、结果准确精度高、界面美观易操作等特点。本文首次将基于MFC的C++程序应用在地势起伏度计算方面,增加了地势起伏度计算的手段,在创新性和实用性方面具有一定价值。
参考文献
[1] 涂汉明,刘振东.中国地势起伏度研究[J].测绘学报,1991,20(4):311-319.
[2] 郑琴文,马维峰,刘文婷,等.三峡库区地势起伏度研究[J].厦门理工学院学报,2014,22(5):82-87.
[3] 冯玉祥,邓青春,杨海青,等.基于变点分析法提取元谋县地形起伏度[J].四川林勘设计,2015(3):28-33.
[4] 王玲,吕新.基于DEM的新疆地势起伏度分析[J].测绘科学,2009,34(1):113-116.
[5] 唐飞,陈曦,程维明,等.基于DEM的准噶尔盆地及其西北山区地势起伏度研究[J].干旱区地理,2006,29(3):388-392.
[6] 何文秀,石云,马超.基于DEM的彭阳县地势起伏度分析[J].宁夏工程技术,2016,15(1):30-32.
[7] 赵斌滨,程永锋,丁士君,等.基于SRTM-DEM的我国地势起伏度统计单元研究[J].水利学报,2015,46(6):284-290.
[8] 聂斐,殷兴辉.基于MFC的实时数据动态显示界面设计[J].电子设计工程,2013,21(10):136-138.
[9] 裴亮,蔡锋,李国庆.DLT程序设计与应用[J].测绘工程,2003,12(4):50-54.
[10] 赖祥芳.选择合适的STL容器[J].数字技术与应用,2015(9):177.
[11] 韩海辉,高婷,易欢,等.基于变点分析法提取地势起伏度——以青藏高原为例[J].地理科学,2012,32(1):101-104.
[12] 项静恬,史久恩.非线性系统中数据处理的统计方法[M]. 北京:科学出版社,1997.endprint
