多变点位置的识别隐马尔科夫链方法
2021-10-25郭卫娟
郭卫娟
(湖北第二师范学院a.数学与经济学院;b.大数据建模与智能计算研究所,武汉 430205)
1 变点问题简介
变点序列数据是数理统计中经常遇见的一个序列,在该序列中,各个子部分的总体的分布并不是一样的,对于这类问题,通常的处理方式是先识别该序列中的变点的位置,然后就可以利用相邻的两个变点之间的分布是相同的,进而来估计该部分的分布。
其一般模型如下:

(1)


2 状态转移概率
为此建立如下模型:在时刻,定义状态(i=0,1,2,…,t-1)表示离t最近的前向变点位置在t-i位置上,记其概率为p(Ct=i|xt-1,xt-i+1,…xt-1),意思即xt-i,xt-i+1,…xi-1这个观测值是独立同分布,例如(Ct=0|xt-i,xt-i+1,…xt)表示xi-1是变点,i=t-1表示该序列无变点。这与传统的马尔科夫链相比,就是将隐马尔科夫链中有限个状态改成成了与当前时刻t相关的一个变量。这样将会导致转移概率矩阵维数无限增大,因此为了最大程度上简化状态转移概率矩阵,为此笔者再假设模型(1)满足如下特征:
p(Ct=i|xt-i,xt-i+1,…,xt-1)=p(Ct-k=i|xt-k-i,xt-k-i+1,…xt-k+1),
也就是连续的i个观测值是同一分布(大部分参考文献称该值为链长,用字母g表示)与该观测值的起点位置无关,这样,整个状态概率概率就简单的由链长的概率分布确定了。考虑到本文是从当前时刻开始,逐步向前查找最近的变点 ,若令p表示每个观察值可能是变点的概率,即
p(xi是变点)=p

=p(1-p)i-1i=0,1,2,…,t-1。即此时链长g服从几何分布Ge(p) 。
实际上为链长g可以为取值于i=0,1,2,…,t-1的任意离散型分布,同样可以计算该分布的生存函数。利用生存函数可以计算出各个状态之间的转移概率。
则有各个状态之间的转移概率计算如下:



(1)若位置t-1是为变点,则此时离t最近的前向变点就是t-1,此时j=0,

(2)若位置t-1是为变点,则此时离t最近的前向变点就是t-1,此时j=i+1,

特别的,若链长g服从几何分布Ge(p),则利用(2)式可知其对应的状态转移概率为:
TP=(t=j│t-1=i)

3 模拟和计算
因为该模型的重点是识别变点的位置,也就是识别当前时刻该序列所处的状态,因此按照隐马尔科夫链模型,主要是学习该模型的参数,然后采用最大后验概率进行模式(隐含状态)识别问题。实际上,本文的主要工作就是从最后一个观察值,采用前向传导算法找出该序列中所有的变点位置。也就是主要是求给定观测值下链长的概率分布。为此采用贝叶斯方法。方法如下:
(1) 初始化令p(C1=0│x1) =0
(2)递推公式:

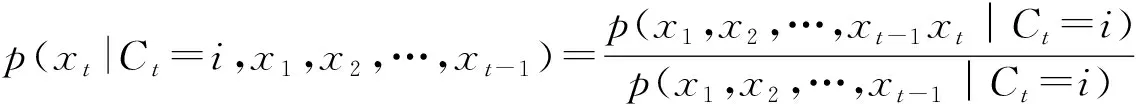
上式p(Ct=i|x1,x2,…,xt)和p(Ct-1=i|x1,x2,…,xt-1)形式一致,因此可以建立二者之间的递推关系,若记b(t,i)=p(Ct=i|x1,x2,…,xt),则有递推公式

由此可以计算出全部的b(t,i),i≤t≤n。
(3)随机模拟方法:令T0=n,k=0,从b(T0,i)抽样,得到Tk,然后令k=k+1,若Tk>0,则继续从b(Tk-1,i)中抽样,这样就得到一序列变点位置,Tk-1,Tk-2,…T1。为提高精度,本文重复抽样1000次,最后用均值估计Tk-1,Tk-2,…,T1。

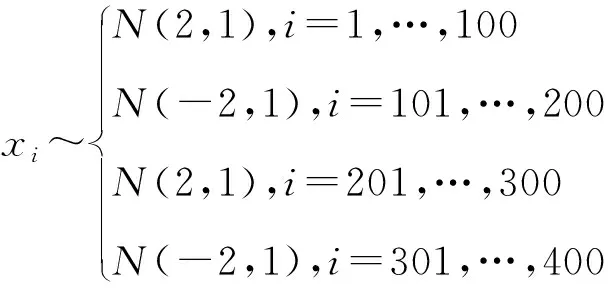
显然模拟数据一共是400个,有4个变点,位置分别位于第100,200,300,400处。因此假设p=0.04.
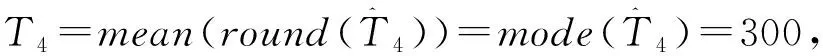

图1 有4个变点的实际图像
实际上,该方法主要问题是求出全部变点位置,而对参数估计值并未做出更多改进,因而,参数估计部分由于不同,必然会带来一定的估计偏差,这是笔者下一步努力的方向。总的来说,该方法不失为多个变点位置估计的一种好方法。
