触及题目的背后——谈高三数列复习

● (常州市第一中学,江苏 常州 213003)

2017-08-30

江苏省教育科学“十二五”规划课题(B-a/2015/02/008)

陆建明(1981-)，男，江苏溧阳人，中学一级教师.研究方向数学教育.

触及题目的背后
——谈高三数列复习

●陆建明
(常州市第一中学,江苏 常州 213003)

文章从2017年江苏省南通市二模数学卷第20题引入，探索此题的背景，指出评讲高三数列压轴题应该兼顾一轮、推而广之、旁征博引，从而真正实现高三复习定位于突出重点、掌握思想、学会探究的目标，即提升能力,力争突破难题.

等差数列;等比数列;好数列

高三下学期复习,在学生系统掌握了基础知识和基础方法后，教学更多的是以练带动复习，此时教师评讲作业如果和学生一样只是就题论题，那么学生怎会有质的飞跃，怎会有深刻认识，并形成深刻的反思！作为教师，要给学生一碗水，自己必需有一桶水，站在更高的高度看待高三复习，复习目标应该定位于突出重点、掌握思想、学会探究，即提升能力,力争突破难题.下面以2017年江苏省南通市二模数学卷第20题评讲为例，站在更高的高度探索数列终极复习.

例1设数列{an}的前n项和为Sn(其中n∈N*)，且满足：

① |a1|≠|a2|;

②r(n-p)Sn+1=(n2+n)an+(n2-n-2)a1,其中r,p∈R,且r≠0.

1)求p的值；

2)数列{an}能否是等比数列？请说明理由；

3)求证：当r=2时，数列{an}是等差数列.

分析1)p=1；2)利用特值法得到{an}不是等比数列,过程略.

3)证明由题意可得

2(n-1)Sn+1=(n2+n)an+(n2-n-2)a1.

当n=1时，上式恒成立.

当n≥2时，

上式赋n为n+1，得

(2)

式(2)-式(1)，得

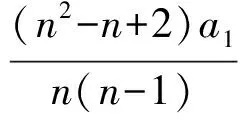
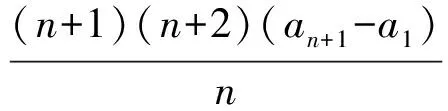
两边同除n+1,得

令bn=an-a1,得

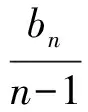
2cn+2=(n+2)cn+1-ncn

即

2(cn+2-cn+1)=n(cn+1-cn).

令dn=cn+1-cn,得

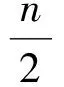
累乘可得

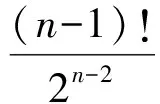
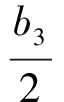
从而

dn=0.

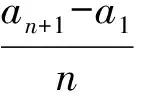
an=a1+(n-1)(a2-a1).

经检验，n=1符合上式.

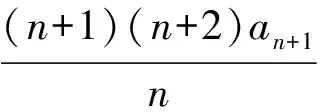
教师引领，站在一定的高度反思这个问题：条件r(n-1)Sn+1=(n2+n)an+(n2-n-2)a1是整个题目的核心，r=2怎么来的呢？事实上，反过来想：如果数列{an}是等差数列，那么可以借助基本量化简得

r(n-1)Sn+1=

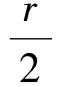
(3)

(n2+n)an+(n2-n-2)a1=

n(n+1)a1+(n-1)n(n+1)d+(n-2)(n+1)a1=

2(n-1)(n+1)a1+n(n+1)(n-1)d,

(4)

对比可以发现，当r=2时，式(3)和式(4)相等，因此可以大胆猜测当r=2时，数列{an}是等差数列.此外，还有其他角度的解释吗？

如果只是满足于解决这一道题目，那么学生不可能发现其背后的问题，更没法做到深度地思考与反思.正好在前面的复习中，我们遇到了一个“好数列”的题目.

例2设数列{an}的前n项和为Sn，我们称满足条件：“对任意的m，n∈N*,均有(n-m)Sn+m=(n+m)(Sn-Sm)”的数列{an}为好数列(问题略).

对于这个问题，我们需要思考的是:上述定义的来源是什么，满足“好数列”的背景是什么？事实上，经过尝试，我们发现等差数列满足上述定义，也就是如果{an}是等差数列，那么可以证得

(n-m)Sn+m=(n+m)(Sn-Sm).

反思第一轮中做过的一道题目：

例3已知数列{an}是等差数列，其前n项和为Sn，且Sn=m,Sm=n(其中m,n∈N*,m≠n)，则Sm+n=-(m+n).

事实上，这是一个很实用的等差数列性质，在文献[1]中有详细解析.由此可以猜想数列中有很多问题都是可以反过来思考的，这与文献[2]的研究思路类似.如：

2)若数列{an}的前n项和为Sn，且对任意的m,n∈N*，都有

(n-m)Sn+m=(n+m)(Sn-Sm),

则{an}是等差数列；

3)若{an}的前n项和为Sn=A-Aqn(其中A是不为0的常数，q≠0且q≠1),则{an}是等比数列；

4)若数列{an}的前n项和为Sn，且对任意m,n∈N*,都有

Sm+n=Sn+qnSm(其中q≠0)，

则{an}是等比数列.

上述含有参数m,n的数列性质，有点类似抽象函数表达式的来源.回到例1，将已知条件作进一步思考：

2(n-1)Sn+1=(n2+n)an+(n2-n-2)a1，

取其中1为任意的正整数m，上式可以变形为

2(n-m)Sm+n= [n2+n-(m2-m)]an+

[n2-n-(m2+m)]am，

我们大胆利用上述思想推而广之.

思路1取m=1，回到例1中的证明.

思路2赋m=2,n=1,得

a1+a3=2a2；

赋m为n+1，得

即S2n+1=(2n+1)an+1；

(5)

再赋m为n+2,n为n-1，得

(6)

由式(5)和式(6)可得

3an+1=2an+2+an-1，

从而 2(an+2-an+1)=an+1-an+an-an-1.

令bn=an+1-an,得

2bn+1=bn+bn-1,

即

2(bn+1-bn)=-(bn-bn-1).

又因为b2-b1=a3+a1-2a2=0，所以

bn-bn-1=0，

即

an+1-an=an-an-1，

故数列{an}是等差数列.

评注上述问题给学生提供了更大的思维空间，并且将问题推广到更一般的情况，让学生从一定的高度进行思考与分析，为日后遇到类似问题提供方法.

例5已知数列{an}的各项均为正数，其前n项和为Sn，且对任意的m,n∈N*,(Sm+n+S1)2=4a2ma2n.

2)求证：{an}为等比数列.

1)解令m=n=1，可得

因为a1>0,a2>0，所以

a2+2a1=2a2，

即

2)证明令m=1,n=2,得

(2a1+a2+a3)2=4a2a4.

令m=n=2,得

S4+S1=2a4,

即

2a1+a2+a3=a4,

从而

a4=4a2=8a1，

于是

a3=4a1.

又(Sn+1+S1)2=4a2na2,(Sn+2+S1)2=4a2na4,两式相除可得

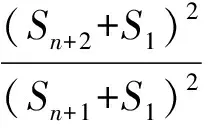
即

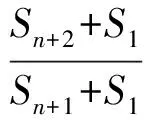
亦即

Sn+2+S1=2(Sn+1+S1)，

进而

Sn+3+S1=2(Sn+2+S1)，

上面两式相减可得an+3=2an+2.经检验：当n≥2时，均有an=2an-1，故数列{an}为等比数列.

数学本身是一个整体，教师只有站在学科的高度看问题，深入挖掘知识点之间的联系，深刻领会数学思想的教育价值，才能充分抓住机会，引导学生从整体、系统的角度进行分析,积极探索数学问题的“本源”，从而积累数学活动的经验，提升数学分析问题、解决问题的能力，提高数学的核心素养.

[2] 陆建根.一道试题的深度研究[J].中学数学教学参考，2016(7):39-41.

O122.1

A

1003-6407(2017)10-20-03