探寻一道统测试题的前世今生
——函数专题复习之以值代参与零点控制
2017-11-07杭州市第十四中学浙江杭州310006
● (杭州市第十四中学,浙江 杭州 310006)
2017-07-02
顾予恒(1981-),男,浙江杭州人,中学一级教师.研究方向数学教育.
探寻一道统测试题的前世今生
——函数专题复习之以值代参与零点控制
●顾予恒李绍塔
(杭州市第十四中学,浙江 杭州 310006)
高考复习不能仅是要把题目做出来,更要研究题目背后蕴含的深刻内涵.文章以2017年浙江省杭州市二模试卷中的一道选择题为例,探究题目本质,追根溯源,探寻题目的前世今生,为高考函数内容复习及加深函数本质理解提供一种示范.
函数;对应关系;以值代参;零点控制
在刚刚结束的2017年浙江省杭州市二模考试中,选择题第9题引起了笔者的注意.学生的得分率不高,有的是通过线性规划的方法把选择题做成了大题,也有的是通过特殊值法猜出了答案,但对本题到底考查了什么内容不甚明了.如果仅以选对答案为问题解决的终点,那么就辜负了命题人的一番良苦用心,不能更好地发挥题目的教育价值.
1 试题呈现
例1设f(x)=x2+ax+b的两个零点为x1,x2,若|x1|+|x2|≤2,则
( )
A.|a|≥1 B.|b|≤1
C.|a+2b|≥2 D.|a+2b|≤2
(2017年浙江省杭州市第二次数学模拟考试第9题)
分析本题是一道与二次函数零点相关的问题,4个选项都值得好好揣摩!
笔者在试卷讲评时设计了以下的问题让学生思考.
思考1如何画二次函数f(x)=x2+ax+b(其中a,b∈R)的图像?
有的说:给我确定的a,b的值,我就能把图像确定下来.这位学生将系数a,b视作二次函数图像变化的一组控制量.
思考2你能画出一个满足题干条件的二次函数图像吗?
有的说:我选取两个满足题干要求的零点,例如x1=0,x2=1,于是图像也被唯一确定下来.这位学生将零点x1,x2视作控制函数图像变化的一组控制量.
方法1由题意知x2+ax+b=0的两根为x1,x2,且x1+x2=-a,x1x2=b.

对于选项A,|a|=|x1+x2|≤|x1|+|x2|≤2,
故选项A不正确.
方法2也可以把|x1|+|x2|≤2视为正方形的可行域,求目标函数|b|=|x1x2|(面积意义)和目标函数|a|=|x1+x2|(线性目标函数)的取值范围(解答略).
评注无论是方法1还是方法2,都源于用函数零点x1,x2来表示参数a,b,本质是在a,b与x1,x2间建立起对应关系.
思考3除了零点,还有没有其他可能的图像控制量?
有学生提出:只要提供函数图像上任意两个点,就可以唯一画出函数图像了.如前面取的两个零点是函数图像与x轴交点的横坐标,即(x1,0),(x2,0)是函数图像上两个特殊的点.

图1
如图1,画出几个临界状态图,如f1(x)=x(x+2),f2(x)=(x+1)2,f3(x)=(x-1)(x+1),f4(x)=(x-1)2,f5(x)=x(x-2).值得注意的是f(x)=x2+ax+b的开口大小已经由二次项系数1决定了,即所有的图像都与f(x)=x2“全等”.
由图1可以发现
即
从而
故
|a+2b|∈[0,4].

至此豁然开朗,这道题的4个选项提供了研究函数问题的一种全新的视角.我们知道,函数最重要的本质是映射(即对应关系),本题可以理解为目标函数在定义域上求值域的问题,关键是将哪个量视为真正的变量,建立起何种对应关系.解决此类问题既可以用函数值来代替参数式(以值代参),也可以用零点关系来代替参数式(零点控制),因题而异,灵活运用.
2 追根溯源
其实这样的视角并非突然从天而降,追根溯源,可以找到众多的前车之鉴.因此研究问题要看它的三生三世,下次遇见时才能十里桃花香.
例2[1]已知函数f(x)=x2+ax+b(其中a,b∈R)在区间(0,1)内有两个零点,则3a+b的取值范围是______.
(2017年浙江省数学高考测试卷第17题)
思考1)求3a+b的取值范围——理解为函数求值域问题;2)变量是哪个:零点;3)对应关系如何?

3a+b=x1x2-3(x1+x2)=
(3-x1)(3-x2)-9∈(-5,0).

图2
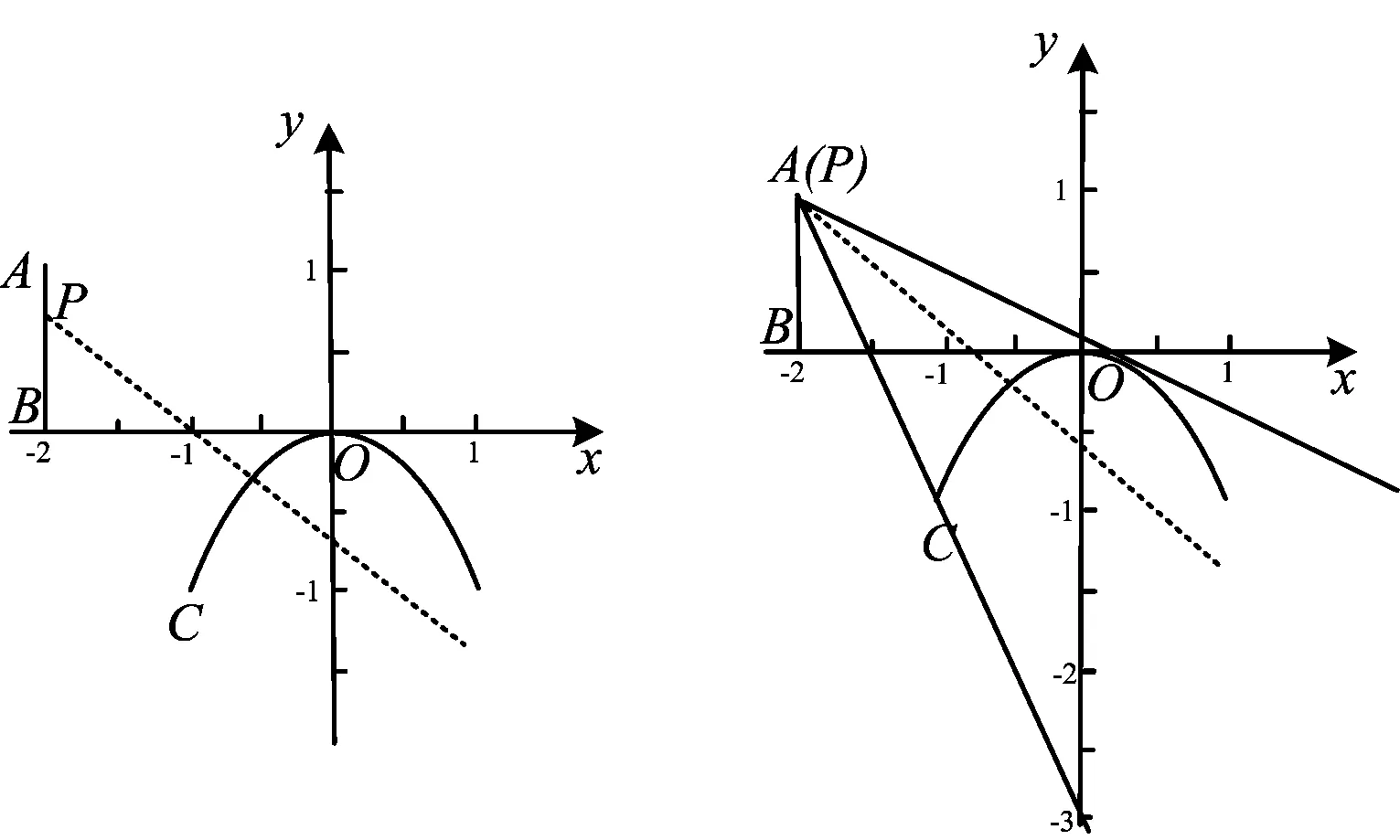
解法2事实上,3a+b=f(3)-9.如图2,画出临界状态的图像,可知f(x)=x2与f(x)=(x-1)2为临界状态,此时4 3a+b∈(-5,0). 评注本题解法1用零点控制完成,最后一步的因式分解是学生们处理的难点,其实它并非从天而降,而是解法2中以值代参的体现. 例3若f(x)=x2+ax+b(其中a,b∈R)在(0,1)内有两个零点,则a2-2b的取值范围是______. (2017年浙江省数学竞赛试题第3题) 解记f(x)=(x-x1)(x-x2)(其中x1,x2∈(0,1)),则 因为x1∈(0,1),x2∈(0,1),所以 评注这道最新的浙江省数学联赛题,在非齐次的目标式a2-2b与零点x1,x2间建立起了对应关系. (2016年浙江省数学高考测试卷第15题) 思考a+b+2c可以视作关于什么变量的函数? 解因为f(0)=c,f(1)=a+b+c,所以 a+b+2c=f(0)+f(1). 由题意知 |f(x)|≤M(a,b,c), 即 -M(a,b,c)≤f(x)≤M(a,b,c), 于是 a+b+2c=f(0)+f(1)≤2M(a,b,c), 即 评注本题将a+b+2c视作由两个函数值f(0)与f(1)一起控制的函数,要求具备良好的识别目标函数的能力. 例5已知b,c∈R,二次函数f(x)=x2+bx+c在(0,1)内与x轴有两个不同的交点,求c2+(1+b)c的取值范围. (2014年浙江省数学竞赛试题第18题) 思考c2+(1+b)c可以视作关于什么变量的函数? 解因为f(0)=c,f(1)=1+b+c,所以 c2+(1+b)c=f(0)f(1). 设f(x)=(x-x1)(x-x2),其中x1,x2∈(0,1)且x1≠x2,则 c2+ (1+b)c=f(0)f(1)= 评注本题和例4如出一辙,与二次函数零点式、基本不等式一同考查,难度有所加大,但还是“原来的配方,熟悉的味道”. 例6[2]设函数f(x)=x2+ax+b(其中a,b∈R),记M(a,b)为y=|f(x)|在[-1,1]上的最大值. 1)已知|a|≥2,求证:M≥2; 2)若M(a,b)≤2,请求出|a|+|b|的最大值. (2015年浙江省数学高考理科试题第18题) 思考1)求|a|+|b|的最大值:函数问题;2)变量是哪个:对于x∈[-1,1],所有的|f(x)|;3)对应关系如何? 因为|a|≥2,即|f(1)-f(-1)|≥4,所以 2M≥|f(-1)|+|f(1)|≥|f(1)-f(-1)|≥4, 从而 M≥2. 2)一方面, |a|+|b|= max{|a+b|,|a-b|}= max{|f(1)-1|,|f(-1)-1|}≤ max{|f(1)|,|f(-1)|}+1≤ M(a,b)+1≤3, 另一方面,当|a|=2,b=-1时,满足M(a,b)=2,此时,|a|+|b|=3. 综上所述,(|a|+|b|)max=3. 评注本题的反解表示,之前很多学生表示看起来都正确却很难想到.如果从以值代参的角度来理解,那么就水到渠成了. 例7[2]设函数f(x)=x2+ax+b(其中a,b∈R),已知函数f(x)在[-1,1]上存在零点,若0≤b-2a≤1,求b的取值范围. (2015年浙江省数学高考文科试题第20题第2)小题) 分析本题可以从规划视角、韦达定理等角度去解决,过程比较繁琐.但如果用代换思想去解决,那么几乎可以秒杀. 解令g(x)=ax+b,h(x)=-x2,则问题可转化为g(x)与h(x)在[-1,1]上的图像有交点. 注意到m=b-2a=g(-2),则直线g(x)=ax+b过点P(-2,m),其中0≤m≤1,即点P(-2,m)在线段AB上运动,如图3所示,b的几何意义是直线在y轴上的截距. 图3 图4 评注本题将函数的零点问题,转化为两个函数图像的交点问题去解决,特别关注题干中出现的参数式b-2a与要求的b的意义. 例8若f(x)=x2+ax+b(其中a,b∈R)在[-1,1]上存在零点,且对任意的t∈[2,3],0≤ta+b≤2,则b的取值范围是______. 分析本题是2015年浙江省数学高考文科试题第20题的改编题,关键在于对条件“对任意的t∈[2,3]总有0≤ta+b≤2”的理解. 图5 图6 评注本题对高考题的改编颇有新意,将点在线段上运动变为线段在矩形区域内运动.若将条件再变化为“存在t∈[2,3],0≤ta+b≤2,”那就与高考题无异了,有兴趣的读者可自行完成. 就教学内容而言,用函数的观点来解决问题,强化函数作为对应关系的理解与应用,是复习函数内容的正确方式.笔者将求目标参数式的取值范围问题视为函数在固定区域上求值域的问题,而“以值代参”与零点控制的技巧都充分体现了函数的对应思想. 高三复习与试题讲解总是密不可分的.试题讲解的第一步,首先是对每一道精彩试题的赏析,只有充分挖掘其内涵和背景,才能发挥试题的最大价值.试题讲解不能只求答案,要让学生知其然,更要知其所以然,这样才能通过讲解少量的试题,就达到让学生“做会一道,通晓一类”的目的. 实现这一目标,要求广大教师不断加强研究,提高自身对数学本质的理解,在高观点下审视数学问题,并通过对教学过程的有效设计和引导,帮助学生更好地掌握数学知识和解题技巧,领会数学思想,形成良好的数学素养. [1] 李学军,曲文瑞.平凡真功显 妙解素养现——由2017浙江省高中数学模拟卷17题说起[J].中学教研(数学),2017(4):39-41. [2] 数学高考研究组.浙江高考数学2004一路走来[M].杭州:浙江大学出版社,2016. O122 A 1003-6407(2017)10-17-04



3 触类旁通


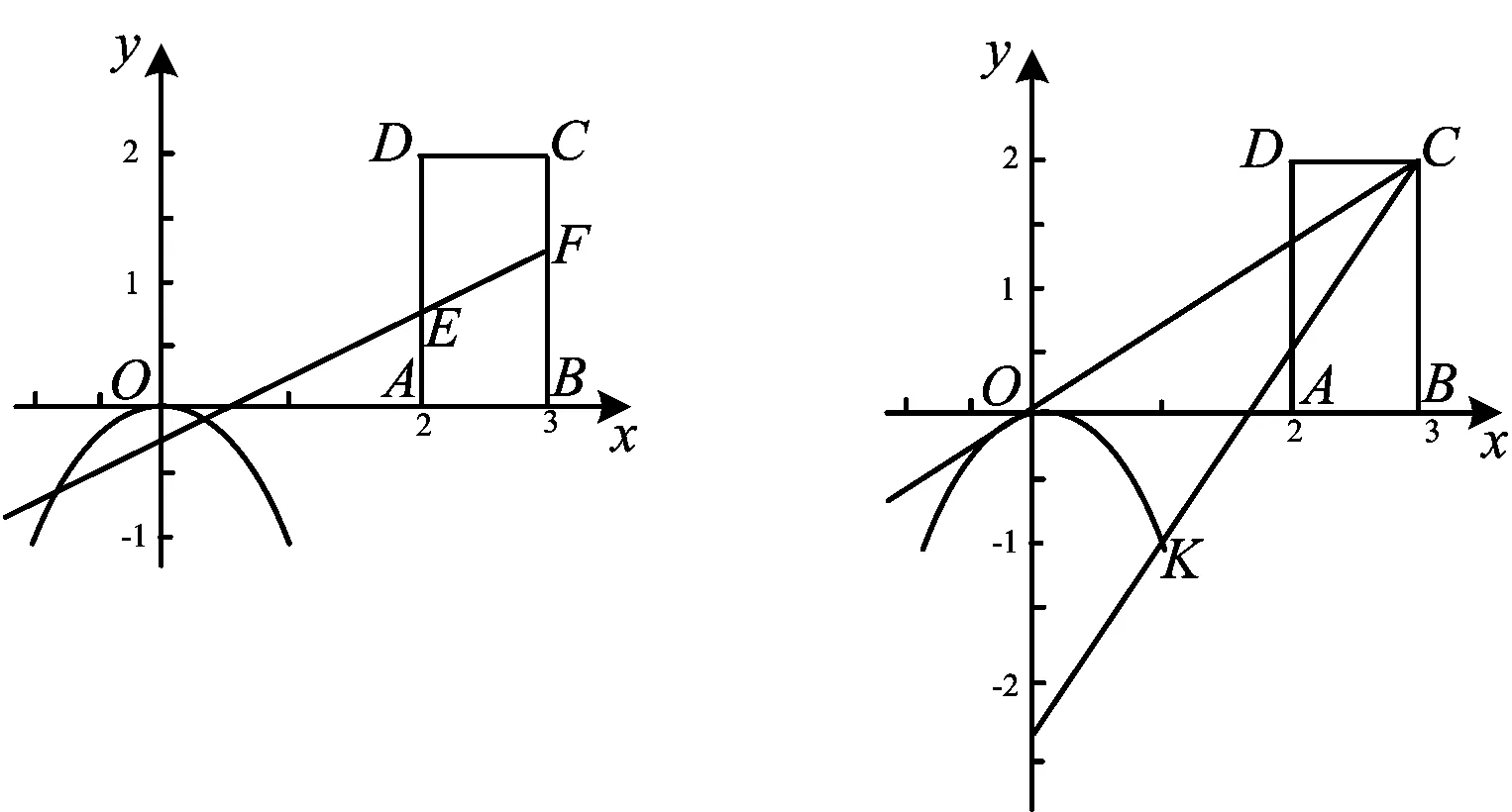
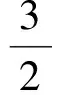
4 教学启示
