基于河流示踪实验的 Bayes 污染溯源:算法参数、影响因素及频率法对比

姜继平,董芙嘉,刘仁涛,袁一星



基于河流示踪实验的 Bayes 污染溯源:算法参数、影响因素及频率法对比

姜继平1,2*,董芙嘉1,刘仁涛1,袁一星1

(1.哈尔滨工业大学环境学院,黑龙江哈尔滨150090；2.南方科技大学环境科学与工程学院,广东深圳518055)

基于贝叶斯理论,结合浓度时间序列方差假定和Adaptive Metropolis MCMC后验采样,建立了用于突发水污染应急溯源的贝叶斯推理方法.该方法结合经验知识和监测事实对源项参数的分布进行推理,直接对溯源结果的反向不确定性用概率分布形式进行表征.依据河流实地示踪剂实验案例,对Bayesian推理溯源的实际效果、后验参数相关性和影响因素等方面进行了验证和测试,结果表明源项参数和方差的后验概率密度的偏度对方差假定敏感,且得到关键参数推荐值:使用RMSE为目标函数;异方差假定中稳定化因子λ1为0, λ2为0.1~0.5;AM采样建议比例因子sd选择0.1~0.3.并对贝叶斯方法和传统基于优化的频率法在求解思路、计算过程、溯源结果等角度进行了深层次的辨析.本研究相关结果为贝叶斯推理技术在污染溯源的实际应用中提供了较为重要的参考价值.

贝叶斯推理；污染源反演；突发水污染；AM采样；河流示踪剂试验

当前,蓄意或非故意的化学品泄露造成的水污染事件仍不断发生.作为典型发展中国家,我国地表水环境一直受到化学品泄露事故的威胁[1-2].其他发展中国家和发达国家,如南非[3]、印度[4]、美国[5]等,也面临类似的困扰和挑战.许多河流污染发生时,污染源未知,肉眼难以辨识.同时不少企业依然存在夜间偷排行为,需要开发基于监测数据的污染源反演技术进行污染溯源.确定污染排放信息是开展应急处置和风险防控的前提[6].

污染溯源技术的理论基础是求解特定情景下的源项反演问题,求解过程融入污染物输移模型.理论上如果对污染输移模型采用负时间步和空间步进行数值计算,应该能求得污染输移历史过程,然而在现实中由于监测误差和数值误差的存在,其不可控的误差反向传播导致了反算结果极大地偏离实际值.该特征就是反问题不适定性的典型表现,也正因为此,在各领域中出现了形形色色的反演技术来求解反问题.

近几年,河流污染源项反演问题开始得到关注,中国学者做了大量工作,提出各类求解方法.例如,解析法[7],基于遗传算法、微分进化算法等的优化法[8-10],地学统计方法[11],反向位置概率密度函数法[12-13],伴随方程法[14]等.都是基于相同的污染物输移、稀释和转化机制,求得源项参数的唯一值,反演结果反向不确定性需要用摄动法等多次计算进行表征.还有从纯数学角度进行污染溯源反问题研究[15-17].2015年后,有人开始从实践角度出发,关注反演的影响因素分析,例如对宽浅河道[18]和二维河道概化下[19]瞬时排放源项反演精度的影响分析.

应用Bayes方法解决科学和工程领域的参数估计研究发展迅速,例如水文学中的地表径流模拟和参数估计[20-22]、土壤环境化学中物化机制的解释[23]等等.近几年,也有人开始将Bayes方法用于水污染溯源,如朱崇[24-26]、毛星[27],陈海洋等[28],曹小群等[29],Wei等[30].有别于确定性的方法,Bayesian反演框架采用信息驱动,组合概率性的先验信息和观测数据中所包含信息,通过贝叶斯推理更新先验信息,得到后验条件概率分布,是不确定性的反演方法,在应急决策风险的不确定性量化方面更有优势.

朱嵩等结合Metroplis-Hastings(MH)采样算法,在假想的10m×4m区域内进行数值实验,反演污染源位置和源强[24,26],这是Bayesian污染溯源较早的尝试,但它更多是框架性、演示性.2012年陈海洋等[28]对Bayesian溯源方法进行了较为细致的推导分析,对关键的误差假设问题进行了初步交代.同样采用MH采样算法,基于更为接近真实水体参数的假想案例对污染源位置、强度河时刻同时反演,并同优化算法进行对比.曹小群等[29]首次采用Adative Metroplis(AM)算法基于假想案例,考虑多点源情形,对污染源位置和强度进行反演.Wei等[30]结合了正向模型参数的不确定性分析,采用AM算法,基于实际河道假想排放情景和数据,对源项三参数进行了反演.

可以看出,目前研究未有人基于实地示踪剂实验和实际的试验监测数据对Bayesian污染源反演方法进行实践测试.特别是需要针对不同特征河流、不同污染排放类型、不同浓度监测精度等实际情形进行对比分析.Bayeisan污染溯源推导过程中关键的误差假定形式没有深入探讨分析,这将影响到似然函数的构建,涉及方法的应用范围.在实际河流尺度和污染排放下,算法参数设置和影响因素也未有报道.Byesian方法同以优化法为代表的确定性方法在计算原理、过程和结果等方面,也未有人进行系统辨析,也有必要结合案例深入探讨.

为此,本文针对突发水污染应急中的污染溯源问题,开展基于河流示踪剂实验的贝叶斯污染溯源研究.采用Adaptive Metropolis算法进行后验概率密度采样,验证与分析不同误差假定下贝叶斯反演技术的有效性、反向不确定性和影响因素,给出操作参数推荐值.并同基于优化的频率法进行对比,深入剖析两者思路、过程和结果的差异.

1 基于Bayesian推理的不确定性应急溯源方法构建

1.1 正向模型

基于污染物对流扩散模型,假设模型参数为常数,污染物在水平和垂直方向上完全混合,通过特征线等方法可以得到不同条件下的水质模型解析解.

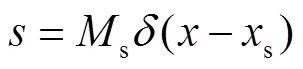
在监测点(,)处的污染物浓度可由下式计算:

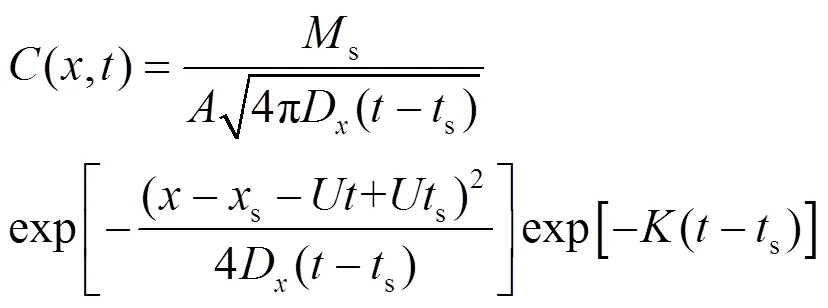
式中:为河流断面面积,m2;D为纵向平均扩散系数,m2/min;为河流平均流速,m;为衰减系数,min-1;为监测时刻,min;为监测点位置,m.

考虑到污染溯源研究中源位置未知,未将坐标原点建立在源排放处和排放时刻.虑到研究问题的特征时间尺度,将时间单位设定为min或者h.

同时对于连续排放源的情境,也可推导出解析解,具体形式可参考文献[31].为对比不同污染传输机制概化的影响,还采用了EPD-RIV1模型[32]和OTIS模型[33]两个基于数值解的一维水质模型.

1.2 应急溯源Bayes理论框架的建立

1.2.1 污染源溯源问题的广义陈述 在河流某断面检出污染物严重超标,在该断面上游开展应急监测,获得个时空采样点的浓度数据,它们和污染物传输机理模型间通过正向模型算子建立联系(式2).该算子即为将模型映射到数据空间的函数.实际上,正向模型算子通常只能是真实物理过程的近似,当使用函数来描述该物理过程时存在系统偏差,可用维向量model来表示.同样也存在一个维向量meas,表示随机测量误差.

式中:为位置污染源参数,为ISP问题中的模型参数.污染溯源的目标是已知监测数据向量估计,或者是的函数(s)[34].需要注意的是,可能是模型边界条件和初始条件而不是模型表达式中的参数.

1.2.2 面向应急溯源的Bayes理论框架 基于污染溯源问题的Bayes公式如下:

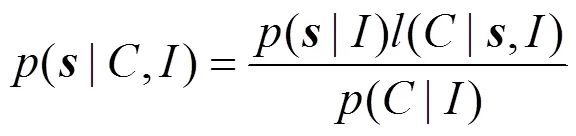
式中:()是源项参数的后验分布,(|)是先验分布,()是似然函数,()是证据,为源项,为浓度监测数据,为背景信息,即用于确定先验分布的信息.

1.2.3 Bayes推理应急溯源方法的建立 基于模型的Bayes推理框架常分为四步:模型构建、后验分布计算、分析后验分布和决策推理[35].

1.2.3.1 第一步:模型构建

(1)溯源问题的Bayesian形式化

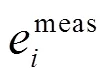
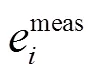
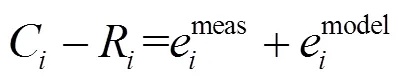
假定这些误差独立(但并不一定同分布),有:

若进一步假定这两类误差都是独立同分布,即所有的meas,i都等于meas,所有的model,i等于model.可推导出似然函数计算公式(7),具体过程可参考[36-37].

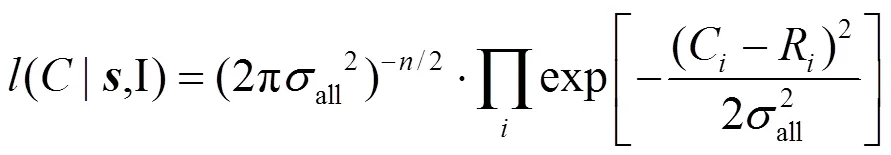
对于异方差非相关误差项,可通过对监测数据进行如下转换而稳定化.Box and Cox[38]证实了它在水文数据中的适用性.

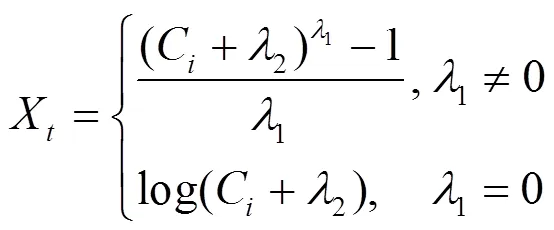
这里,1能从平均残差中估计得到.如果区间平均残差随总平均残差线性增加,就设置1为0.5.如果方差是二次方增加,就设置1为0[20].

基于异方差非相关误差项假定的似然函数可以写为:

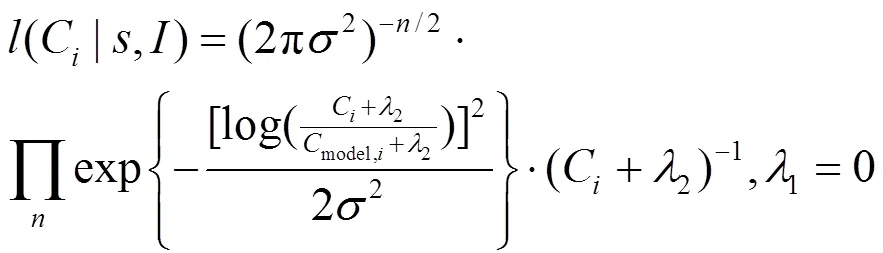
式中:是X的方差.

(2)设置先验概率

用Bayes方法处理统计推理问题的前提是给出参数的先验分布.在文献中提及的方法有客观法、主观概率法、同等无知原则法、共轭先验分布等.在水文学中,常用客观法即经验贝叶斯法,基于大量历史观测数据,如径流量等,得到先验分布,常用的有Gamma分布,正态分布,均一分布等.

河流污染应急溯源中的先验信息常常有限,因此选择均一分布作为优先考虑的先验概率密度函数.当然,如果河流某区段存在大量风险源,如化工区、养殖场等,可优先考虑该污染源出现在该区段的可能性,从而设置综合的概率密度函数.

均一分布的先验概率密度可如下描述:

(|)=常数,∈Real (10)

(3)后验概率密度函数

基于同方差非相关误差项假设的后验概率密度函数可由如下公式描述:

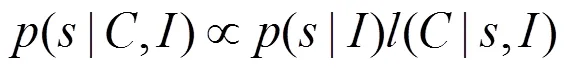
式中:(.)为指示函数.

1.2.3.2 第二步:计算后验分布-MCMC采样

后验分布常常同先验分布是非共轭的,难以近似求解或者是全条件分布,不像已知的任何一个分布.Markov Chain Monte Carlo(MCMC)常被用来快速估计后验分布.最常用的两种MCMC方法是:Metroplis-Hastings(MH)算法[39-40]和Gibbs采样[41].

Marshall等[20]经过一个全面的MCMC算法对比实验后,建议在降雨-径流机理模型中使用Adaptive Metropolis(AM)算法.本文也采用AM算法作为采样方法.

1.2.3.3 第三步:分析后验概率密度

MCMC采样最后收敛到后验概率密度(或者其对数形式),对样本进行统计,如均值、方差、中值、分位数、偏度等可以得到对后验概率密度的描述性统计分析结果.另外,也可以采用数值积分的方法,对各参数的边缘概率密度进行统计.例如,对于s有:

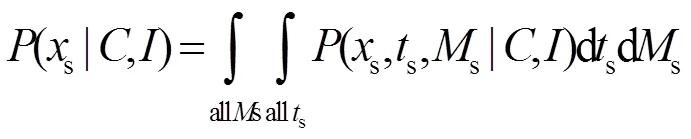
1.2.3.4 第四步:对结果进行推断

依据上述统计分析结果,对污染源信息做最后推断.本文采用中值和贝叶斯区间对源参数结果进行推断.此外,在实际应急响应过程中,还需要结合物理方法进行实地验证,才能最后确定污染源信息.

1.3 后验概率密度采样的AM算法

1.3.1 Markov链及其收敛 Markov链是一个未来状态只和当前状态有关而与过去状态相独立的随机过程.数学上的定义及Markov链收敛到稳态分布的严格数学分析和证明可以参见文献[42].

1.3.2 Adaptive Metropolis算法 Adaptive Metropolis (AM) 算法是一种较好的改进后的MH算法[26,43].其特征是MH算法中的建议PDF基于参数后验协方差得到.该后验协方差矩阵是由过去的迭代结果计算得到,而且每一步都会计算该协方差矩阵.这样,建议分布通过刚刚获取的后验分布信息进行更新.在第步[43],考虑用一个多变量正态分布来表示建议PDF.其均值用当前样本的平均值,而协方差采用矩阵.该协方差矩阵在前面0步中已经固定了一个值0并且通过下面的方式进行后续的更新:

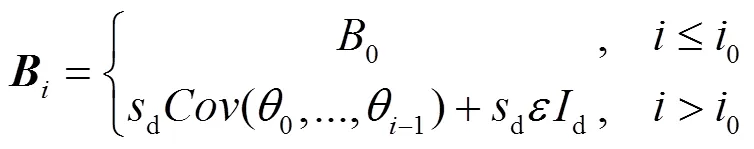
式中:是一个数量很小的参数,被用来确保B不会变得奇异,sd是比例参数,依赖于参数向量的维数,确保建议状态有合理的接受率(例如25%~75%).第+1个迭代步的协方差计算成本较低,它符合下面的公式:

建议协方差的计算需要定义一个任意的初始协方差0.为让该过程自动进行,设置这个初始协方差为先验分布条件下的参数的初始协方差,例如最初的5%迭代步长的参数的协方差.

综上,实现AM算法的步骤如下:

(1)初始化=0

(2)a. 为当前迭代步选择B,采用公式(13)计算.

b. 为生成建议参数值*,其中*~N(θ,B).

c. 计算接受率:

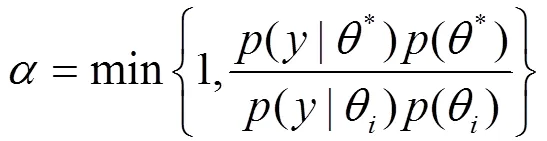
式中:(|) 是似然函数,()是的先验分布.

d. 生成~U[0,1].

e. 如果<,接受θ+1=*,否则设置θ+1=θ.

(3)重复步骤(2).

对于参数值在约束区间外的情形,设置接受率为零.AM算法的一个最大优点是整个参数集同时被更新,减少了计算时间和复杂度.这对于参数高度相关的情形尤为适用(后面可以看到,溯源计算会出现此情形).它与大多数经典算法不一样,后者对每一采样得到的参数需要有不同的建议分布,致使在参数分块采样(block)时极大增加了复杂度.AM采样的有效性和遍历性特征,可参考文献[44].

1.3.3 Markov链的收敛诊断 诊断Markov链收敛方法已经很多[45],其中最为常用是Gelman 和Rubin 1992年开发以及Raftery和Lewis于同年开发的统计方法.本文采用Gelman-Rubin潜在规模减缩因子(potential scale reduction factor, PSRF)来诊断模型的收敛.R的计算如下所示:

式中:是次平行采样链条的平均值的方差,是个链内方差平均值, df是渐进Student t分布的自由度.更多信息可参见文献[45].需要注意的是,PSRF统计是基于多条链平行采样的结果,假如是单一长链采样,可以把链分为三段进行统计.另外通过样本轨迹图也可以对收敛性做出定性分析.

2 基于实地示踪实验的污染溯源

2.1 示踪剂实验

结合论文研究目标,寻找到USGS开展的三个典型河流示踪剂实验用于污染溯源研究,重新构建溯源情景并整理其监测数据.其中以Truckee River示踪剂实验为主,用于算法验证; Lagan River 和West Hobolochitto Creek示踪剂实验为辅,用于对比和影响因素分析.这三个案例有着不同的河道形态与水动力特征及污染物排放特征,案例分别标识为Case-T1,T2和T3.

2.1.1 Truckee River示踪剂实验 Truckee River位于美国加利福尼亚州Tahoe City和内华达州Vista之间.Rivord等在2006~2007年间进行了三次示踪剂实验,为管理河流发生的突发污染事件和污染传输预测提供数据支持.当时河流流量介于143ft3/s和2660ft3/s之间.荧光罗丹明B(RWT),即示踪的‘污染物’,沿此河流三个位置注入,在下游监测其流经过程,具体操作和说明在文献[47]和[48]中有详细介绍.基于上述示踪剂实验,Rivord等人率定并建立了Truckee River的OTIS模型.

本文采用Truckee River中段进行的示踪剂实验.中段长约44km,设置4个采样点(6~9号站点).2006年7月29日6点5分,1.3kg RWT在5号点释放,接近加利福尼亚特拉基的Glenshire Driver,示踪剂浓度数据在6~9号点检测得到.

2.1.2 Lagan River示踪剂实验 2004年11月与2005年4月间,在北爱尔兰的Lagan River进行了8次示踪剂投放实验,用来测量河流的复氧系数[49],试验河段长2.6km.2004年12月10号进行的B号测试监测数据用于溯源反演.惰性气体氙、氪在6个大气压下通入水中耗时30s,31.8min后,在下游1200m 和2600m 处的站点1和2监测穿透曲线,采样每隔数min进行1次.更多细节见文献[49].

2.1.3 West Hobolochitto Creek示踪剂实验 Rathbun于1975年7月在美国密西西比州West Hobolochitto Creek进行了多次气体示踪剂实验来测量大气复氧速率系数[46].West Hobolochitto Creek为一条水文特征复杂既有死水区又有激流的小溪.研究河段长4190m,实验时河流处在低流量条件.

本研究采用了Rathbun的“2号实验”. Rathbun通过多孔管扩散器在100分钟左右的时间内将1.9kg乙烯示踪剂气体注入到河流中.同时,水溶性RWT在同一地点注入.两示踪剂的浓度在注入点下游五个站点进行监测.有关示踪实验更多细节可参考[46].本研究将用于溯源反演的应急监测情景设置为:在示踪剂释放点下游2680m、3370m、4190m处设置3个监测站点在示踪剂排放后的389分钟时开始监测,持续了3.5h,每十分钟采样1次.

2.2 正向模型参数化

采用Truckee River中段示踪剂实验案例(Case-T1)进行溯源反演.正向模型首先采用点源污染瞬时排放一维模型(式1),模型参数设置见表1.

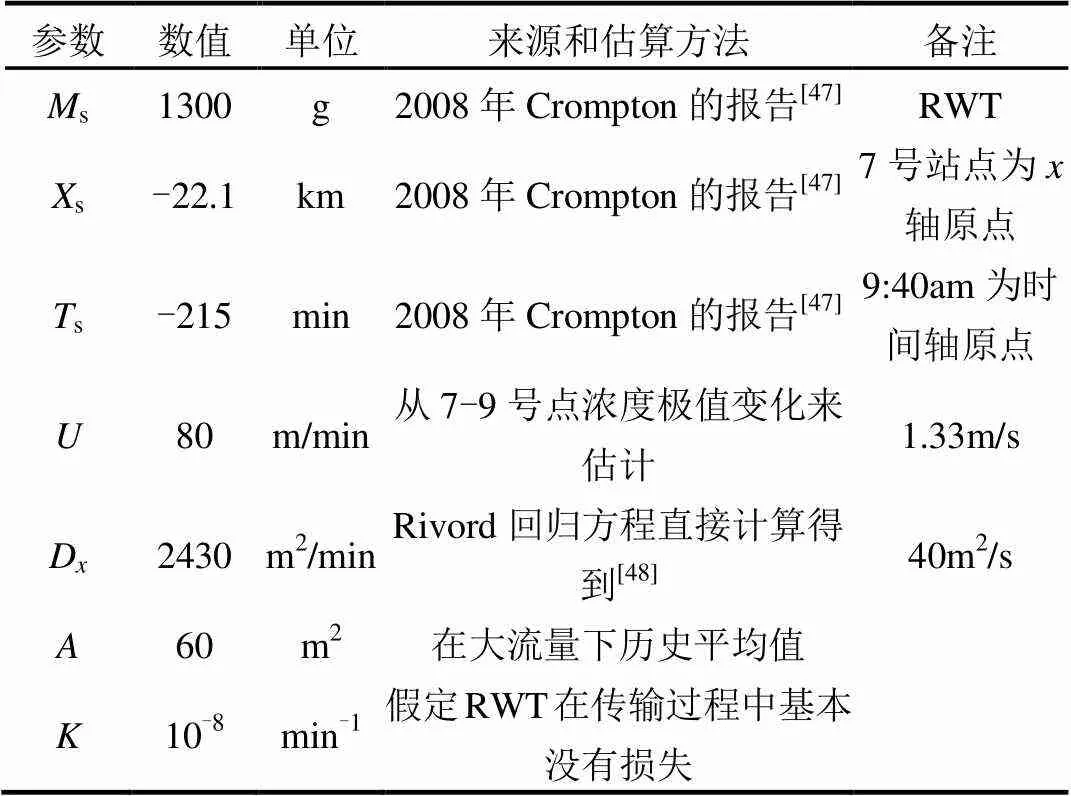
表1 Truckee River案例源项参数和正向模型设置

2.3 采样算法参数设置

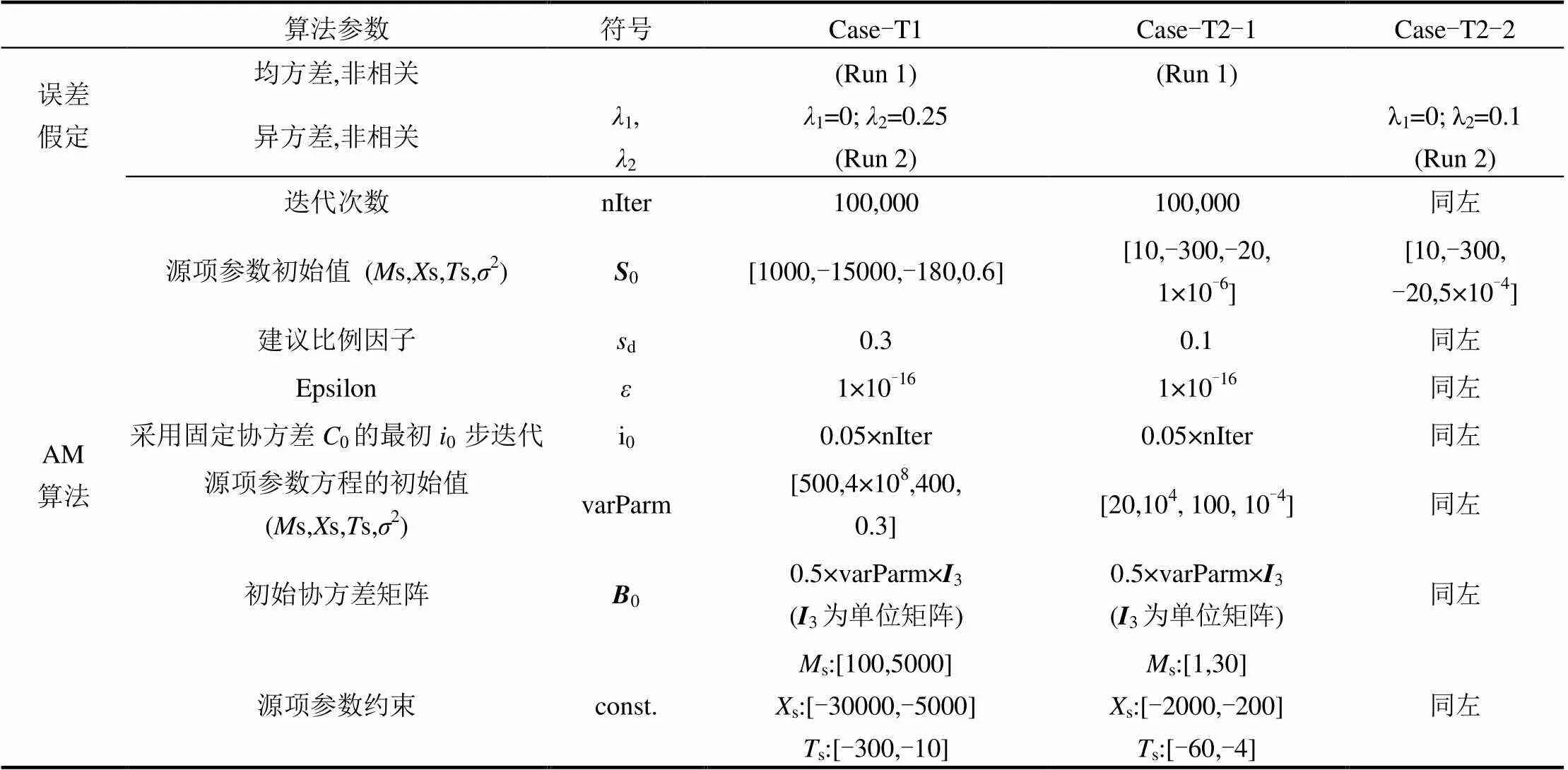
表2 Truckee River案Bayesian溯源中AM采样参数设置

污染源参数分布设定s~U(100,5000),s= U(-30000, -1000),s=U(-300,-10),其中U为均一分布.先验概率密度就是它们的联合分布.同时先假定误差均方差非相关,似然函数用(7)式表示.采样次数设定为100,000,起初20,000次不参与最后样本统计,只取后面80,000个Markov链样本进行分析,考察后验概率密度及不确定性.如果在初次运行中接受率未处于25%~75%,需要人工交互通过调节建立比例因子(proposal scaling factor, sd)来调整建议密度.另外,算法实现中对似然函数进行了对数处理,其他参数设置在表2中.

2.4 溯源反演结果

Case-T1溯源计算结果显示总体PBIAS(平均值百分比偏差)为95%,接受率为35%,在可接受范围内.污染源反演后验分布的概要统计量列在表3中.用样本均值表示对污染源的参数估计.

可见溯源结果与真实污染源情况非常接近而且标准差很小,Bayesian算法很好的完成了应急溯源.从偏度(skewness)、均值(mean)和中值(0.5)的一致性可以看出,s,s,s的边缘PDF基本对称,但方差2呈正偏态.为0.05的最高概率密度区间,即贝叶斯区间(Bayesian interval),表明s不确定性最大,而s贝叶斯区间最小.

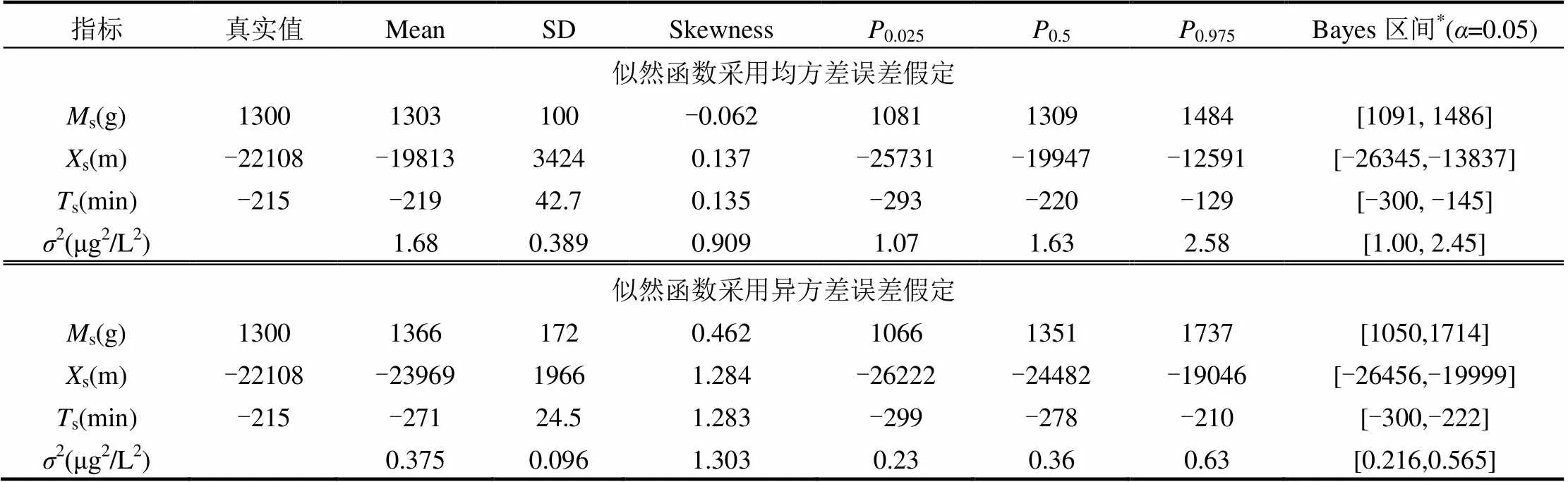
表3 Case-T1(Truckee River)反演结果的概要统计量

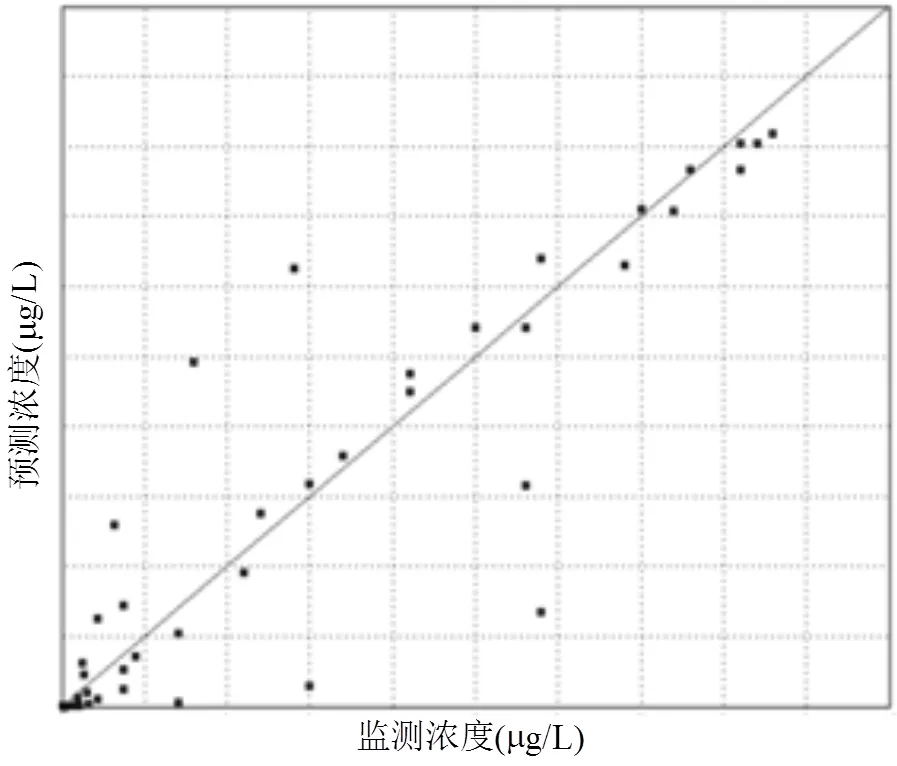
图1 监测浓度和正向预测浓度值对比

PDF曲线通过高斯核对Markov链中后80,000个样本进行估计得到.PDF曲线形态也定性佐证了上述分析结论.

图1表示在后验概率密度极值处计算得到的污染源参数浓度值与实测浓度值,数据对称集中地分布在=直线两侧.表3也对后验分布百分位数0.025、0.5和0.975进行了统计.全部迭代过程后验参数及其均值迭代轨迹绘于图3和图4中.可以看出,在大约40000步后,所有参数Markov链收敛于极限分布.Gelman-Rubin PSRF诊断得到4个参数的值分别为1.0470, 1.0361, 1.0362, 1.0017,接近于1,也说明Markov链收敛.自相关函数(Autocorrelation function, ACF)分析表明当迟滞大于30个迭代步后,ACF较小,残差均值相关性弱.高ACF意味着链内低混合,常会导致收敛到后验分布较慢.

至此Bayesian推理应急溯源技术完成了反演计算,给出了源项后验信息概率分布形式的结果.在应急响应中,响应人员可以在均值正负一个标准差的范围内,或者贝叶斯区间的范围内进行污染源位置物理搜索和化学确认.对污染物排放总量和时刻也可进行同样的推理.

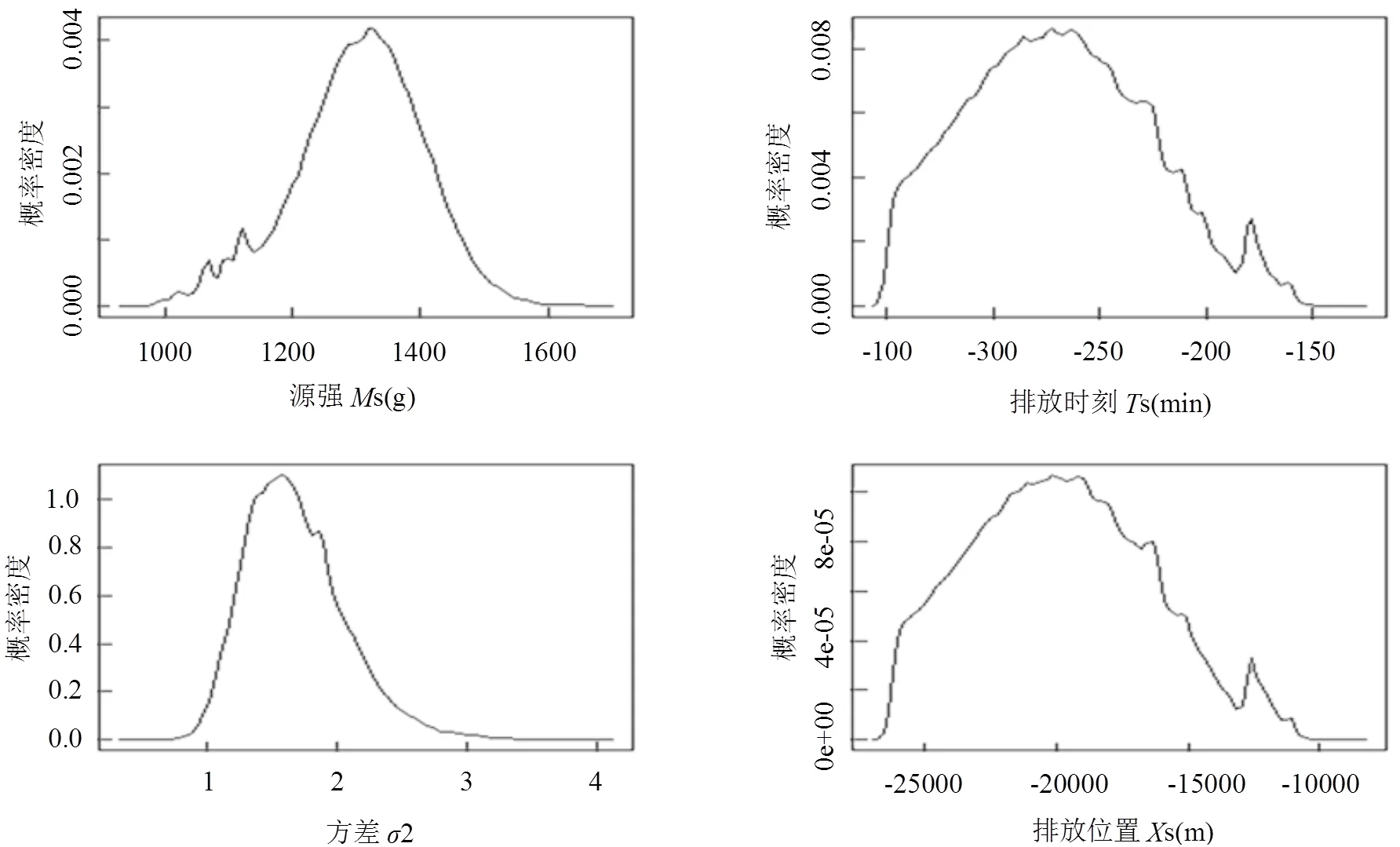
图2 源项参数和方差的后验概率密度曲线

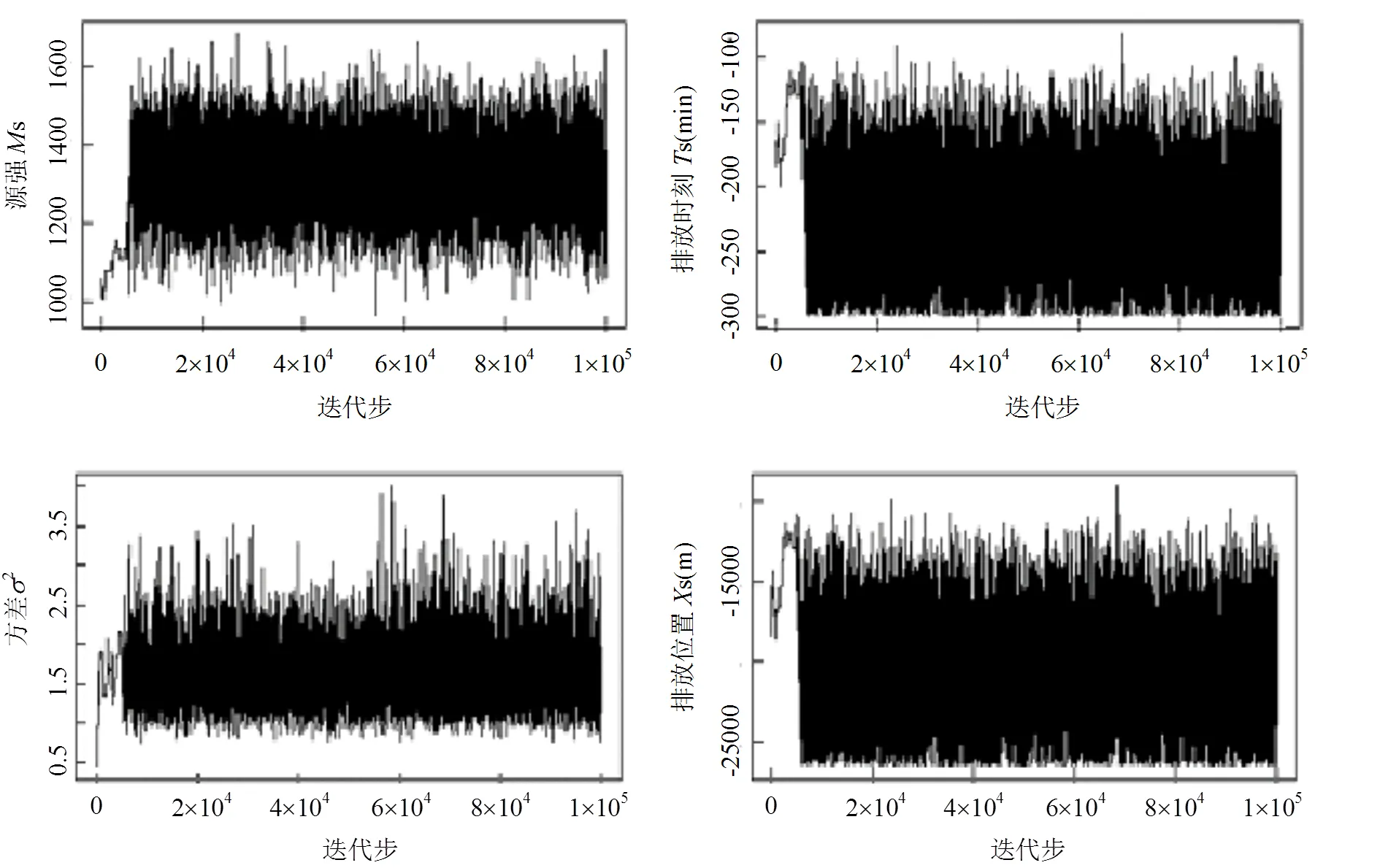
图3 源项参数和方差σ2的迭代轨迹

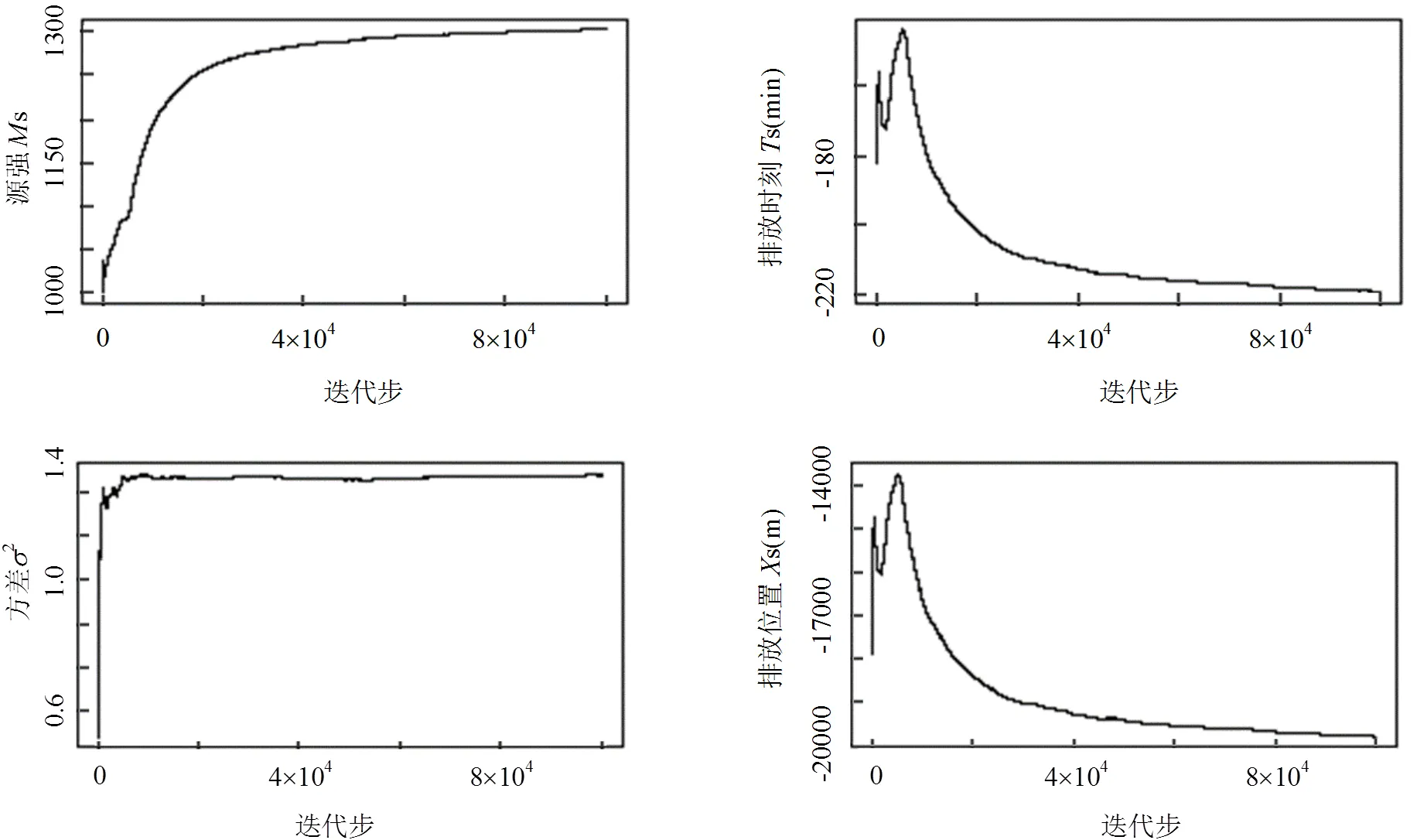
图4 源项参数和方差σ2在MCMC采样过程的均值变化

3 Bayesian推理应急溯源的影响因素分析

3.1 参数相关性分析

源项参数间的相关性必然会对反演结果的分布形式造成影响.对Case-T1案例后验样本中源项参数相关性分析发现s和s的相关系数高达0.999,说明两者存在依赖关系.高相关性容易导致收敛到后验分布变慢,前面研究可以看到Markov链经过上万步迭代才收敛.

实际上,分析无量纲对流扩散方程(式17)即可发现两者确实存在着依赖关系.该线性偏微分方程中系数只有Peclet准数,,该线性系统结构的差异只依赖于参数.小Peclet准数流动是扩散控制而大Peclet准数流动则是对流控制.

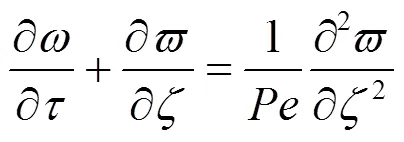
只需确定几何特征尺度,其无量纲时间就可确定,定义应急监测断面间的平均距离为. Truckee River 案例中,以10km计可以计算出为329,为对流控制.对于Case-T2,特征尺度取600m求得为11.7,反演参数相关性将要比Case-T1小.事实上,通过计算发现Case-T2溯源反演源项参数的后验样本中s和s相关系数为0.8,较Case-T1小很多.

3.2 浓度时间序列方差假定的影响

首先考察不同误差项假设的影响.对基于异方差假设似然函数的方法进行计算,结果也列于表3中.可以看出除s的反演结果比均方差假设的结果大外,两者的相差不太大.但是后者的偏度都比较大,正偏斜,说明参数后验PDF的偏度对误差假定是敏感的.Bayes区间也要较同方差假设要小一些.

可初步推断,s和s更适合于用同方差假设而s适合异方差假设,可能也是由混合区影响所致.对于s,不同监测断面距混合区距离不同,造成实测数据同正向模型计算间偏差不同,从而导致异方差的分布形式.这一结论同样被小尺度Lagan River案例所证实.需要注意的是,在具体应用中异方差假设需依据历史观测数据去调节稳定化因子λ1和λ2,这在数据稀缺的环境下存在一定困难.

3.3 后验概率密度采样方法的影响

考察了传统的Metropolis采样和AM采样方法对Case-T1和Case-T2反演结果的影响.其后验参数的差别不大,但是由于传统的Metroplis采样需要对建议概率密度进行测试,比较麻烦.而AM采样方法调节的参数少,不需要考虑寻找合适的建议概率密度函数.

3.4 污染物传输机制概化的影响

对比EPD-RIV1数值解模型和解析解模型的溯源计算可知,前者基于有限差分求解线性代数方程组而后者基于一个代数方程,计算复杂度差一个数量级,所以前者溯源计算要慢些.EPD- RIV1模型可考虑不同曲线形式的污染源输入,更适用于排放历史重构.

OTIS模型和解析解模型溯源计算结果差异不大,主要是因为Truckee River河段不存在死水区.但是由于OTIS模型多了三个参数,河流断面面积、死水区断面面积和死水区同主流区间的传质交换系数,需要更多的事前率定工作,在实际操作过程中比较麻烦.

4 Bayesian推理溯源方法和确定性优化法的对比辨析

传统优化算法,如遗传算法,也能够快速求解简单情景下的污染反演问题,其策略如图5所示.然而优化算法和贝叶斯算法进行溯源分别对应了频率主义(Frequentism)和贝叶斯主义(Bayesianism)两个方法论,目前尚未有人对两者在污染溯源问题上结合案例进行对比辨析,有必要在思路、过程和结果上进行剖析,有益于应用实践.

频率主义和贝叶斯主义的本质区别是对概率定义的差异.前者认为概率表示有限次的重复测量,后者认为概率是对事件认识程度的度量.这两学派围绕此问题在上世纪60年代展开了长久的争论[50-51].关于频率学派和Bayes 学派方法论上区别的更多探讨和解释可参考相关文献和网络资料[50-52].

本文进一步采用遗传优化算法对Case-T1进行溯源计算,重复运行20次统计其结果,见表4. 需要注意的是,也可以采用bootstrap或jackknife重采样进行统计.

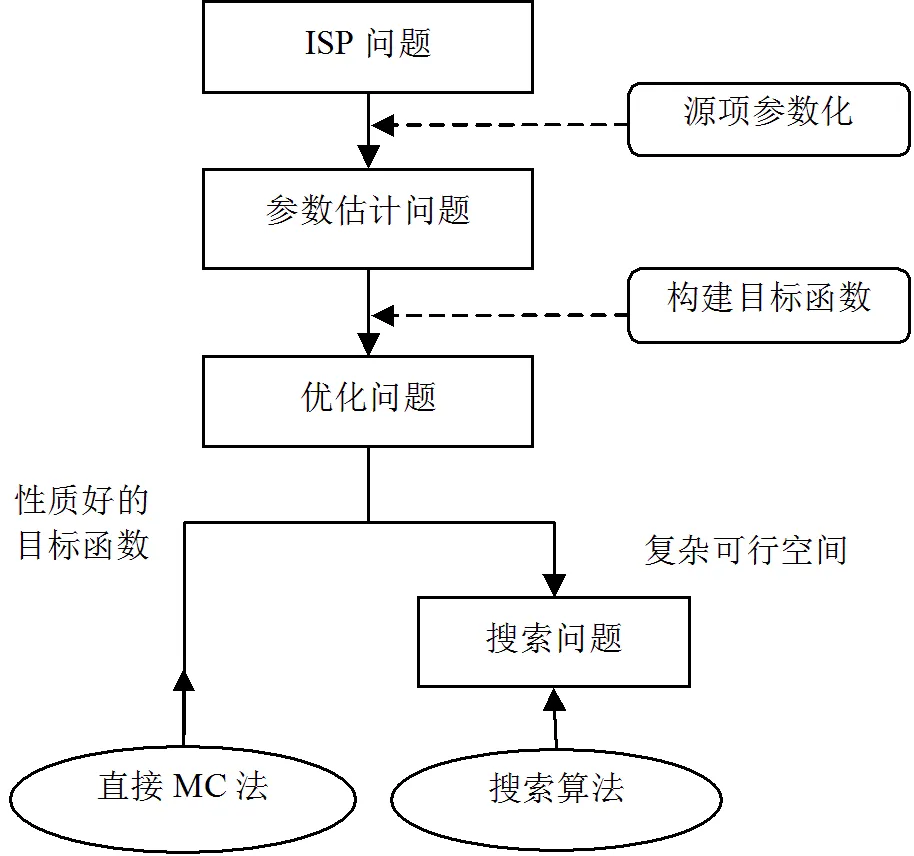
图5 基于优化法的污染溯源求解策略

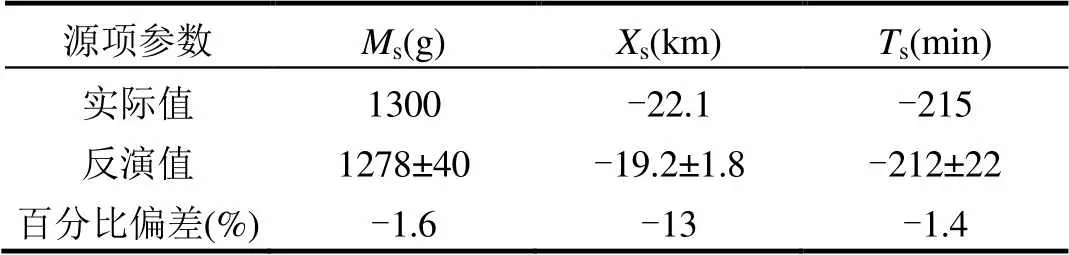
表4 基于遗传算法优化求解的Case-T1反演结果

4.1 求解思路的差异分析

在优化方法中,源项参数是未知固定量,通过优化可以找到这个值或者说可能值.一次优化模拟求得一个最优解,就可以看成一次试验.运行20次对最优解进行统计,用中值和标准差来描述反演结果就是采用了频率的观点.在此,观测数据和正向模型捆绑在一起,参与重复随机试验.

对于本文的Bayesian框架,把源项参数看成未知随机变量而观测数据是确定的知识和信息.溯源反演中估计的是随机变量在特定场合下所取的特定值.例如,可进一步解释:“根据以前对的了解(先验分布)以及现在观察结果(浓度样本C)推断:未知s有60%的可能性在-20km到-40km之间,有30%的可能性-60km到-40km之间.”当然,如果需要一个更确定的解释,可采用后验分布均值(本论文采用该方法)和广义极大似然估计(似然函数最大的位置)等.

此外,Bayesian框架中MCMC只不过是对后验分布的采样,如果可以直接求解似然函数积分方程就可不用MCMC采样.这和图5中直接Monte Carlo法作用完全不一样.两个方法中样本(浓度数据)所起的作用不一样.在Bayes学派中,样本的唯一作用是在于它使对所要估计参数()的认识起了变化.

4.2 计算过程的差异分析

可以说,优化应急溯源是为解决直接蒙特卡洛暴力求解低效耗时的缺点而建立,而Bayesian推理应急溯源是为解决反向不确定性量化困难而建立,两者的计算过程也显然存在差异.从计算复杂度上看,优化算法控制步骤通常为正向计算过程,而Bayes方法控制步骤为后验采样.两者计算收敛都需要调节算法参数来获得.另外,Bayes方法要求应用者对算法参数有一定了解.

在计算过程中,Bayesian推理更多从信息论的角度分析和求解问题,而优化方法更多是数学角度.例如Bayeisan框架中似然函数设置时需要对误差项做出假设,不同假设就附带了对给定问题的不同理解和分析.对先验分布所做的假设也是如此.在Bayesian框架求解过程中注入了不同信息.而对后验分布的分析和推理也是提取信息的过程,优化法中只考虑选择什么样的正向模型,一旦确定后就不考虑其他可用信息.

4.3 溯源结果的差异分析

对Truckee River示踪实验案例的溯源结果进行对比,两者在均值上表现基本一致,尽管Bayesian方法得到的反演结果要略接近真实值.优化法没有给出置信区间(也可通过前述的bootstrap法近似给出),Bayesian推理通过后验样本得到Bayes信任区间为决策者提供决策信心.

在两个方法对标准差的解释也有差异.优化法是20次运行中最优解统计得到的标准差,不能认为是源项参数概率分布的描述.Bayesian方法基于MCMC采样通过参数后验分布而得到标准差,源项参数反向不确定性定量的客观描述,因此更有意义.从而在确定溯源反演方法后,在真实污染事件的溯源反演过程中提高污染物传输建模的精度是减少结构不确定性提高反演准确度的关键之一.

5 结论

5.1 针对贝叶斯推理技术在河流突发污染溯源实际应用中存在的问题,结合实地示踪剂实验数据,开展算法参数、影响因素、同频率法对比辨析的研究. 针对传统MH算法建议密度选择的问题,采用AM算法进行后验概论密度采样;针对监测污染物浓度时间序列不同方差情形,建立不同的似然函数进行溯源.三个示踪剂实验案例,基于AM采样的贝叶斯反演都取得了较好的结果.验证了贝叶斯方法在实际污染溯源中的适用性.

5.2 污染传输的物理机制中源项参数排放时间s和排放时刻s存在固有的相关性,对反演准确度造成影响.源项参数和方差的后验概率密度的偏度对方差假定敏感.对算法使用的目标函数,异方差假定中稳定化因子λ1、λ2,AM采样建议比例因子sd等参数都给出了推荐值.这为贝叶斯推理技术在污染溯源的实际应用提供了较为重要的参考价值.

[1] Xue P, Zeng W. Trends of environmental accidents and impact factors in China [J]. Frontiers of Environmental Science & Engineering in China, 2011,5(2):266-276.

[2] 曲建华,孟宪林,尤 宏.两阶段评估体系筛选水源突发污染应急最优技术方案 [J]. 中国环境科学, 2015,35(10):3193-200.

[3] Staff Reporter. Crocodile River water affected by toxic spill [M/OL]. 2005[2017-03-05].http://mg.co.za/article/2005-12-23- crocodile-river-water-affected-by-toxic-spill.

[4] India Environment Portal [M/OL]. 2017[2017-03-05]http://www. indiaenvironmentportal.org.in/category/thesaurus/water-pollution.

[5] NRC. National Response Center (NRC) data download [M/OL]. [2017-03-05] http://www.nrc.uscg.mil/download.html.

[6] 王圣瑞,张 蕊,过龙根,等.洞庭湖水生态风险防控技术体系研究 [J]. 中国环境科学, 2017,37(5):1896-905.

[7] 陈媛华,王 鹏,姜继平.基于相关系数优化法的河流突发污染源项识别 [J]. 中国环境科学, 2011,31(11):1802-1807.

[8] 彭亚绵,刘春凤,杨爱民.二维对流一扩散方程反问题的遗传算法求解 [J]. 河北理工大学学报(自然科学版), 2008,30(2):84- 87.

[9] 辛小康,韩小波,李 建.基于遗传算法的水污染事故污染源识别模型 [J]. 水电能源科学, 2014,32(7):52-55.

[10] 牟行洋.基于微分进化算法的污染物源项识别反问题研究 [J]. 水动力学研究与进展A辑, 2011,26(1):24-30.

[11] Boano F, Revelli R, Ridolfi L. Source identification in river pollution problems: A geostatistical approach [J]. Water Resources Research, 2005,41(7):1-13

[12] Cheng W P, Jia Y. Identification of contaminant point source in surface waters based on backward location probability density function method [J]. Advances in Water Resources, 2010,33(4): 397-410.

[13] 王家彪,雷晓辉,廖卫红.基于耦合概率密度方法的河渠突发水污染溯源 [J]. 水利学报, 2015,46(11):1280-1289.

[14] 吴自库,范海梅,陈秀荣.对流－扩散过程逆过程反问题的伴随同化研究 [J]. 水动力学研究与进展, 2008,23(2):111-115.

[15] Hamdi A. Inverse source problem in a 2D linear evolution transport equation: detection of pollution source [J]. Inverse Problems in Science and Engineering, 2012,20(3):401-421.

[16] Hamdi A. Identification of point sources in two-dimensional advection-diffusion-reaction equation: application to pollution sources in a river. Stationary case [J]. Inverse Problems in Science & Engineering, 2007,15(8):855-870.

[17] Hamdi A. The recovery of a time-dependent point source in a linear transport equation: application to surface water pollution [J]. Inverse Problems, 2009,25(7):6-23.

[18] 吴一亚,金文龙,吴云波.宽浅河道瞬时源源项反问题及反演精度主要影响因子分析 [J]. 水资源保护, 2015,31(5):58-61.

[19] 高 琦,韩龙喜,陈丽娜.平面二维河道瞬时源反演及反演精度影响分析 [J]. 四川环境, 2016,35(3):67-72.

[20] Marshall L, Nott D, Sharma A. A comparative study of Markov chain Monte Carlo methods for conceptual rainfall-runoff modeling [J]. Water Resources Research, 2004,40(2):1-11.

[21] Campbell E P, Fox D R, Bates B C. A Bayesian Approach to parameter estimation and pooling in nonlinear flood event models [J]. Water Resources Research, 1999,35(1):211-220.

[22] Bates B C, Campbell E P. A Markov Chain Monte Carlo Scheme for parameter estimation and inference in conceptual rainfall- runoff modeling [J]. Water Resources Research, 2001,37(4):937- 947.

[23] Loos M, Krauss M, Fenner K. Pesticide Nonextractable Residue Formation in Soil: Insights from Inverse Modeling of Degradation Time Series [J]. Environmental Science & Technology, 2012,46(18):9830-9837.

[24] 朱 嵩.基于贝叶斯推理的环境水力学反问题研究 [D]. 浙江大学, 2008.

[25] 朱 嵩,刘国华,毛根海.利用贝叶斯推理估计二维含源对流扩散方程参数 [J]. 四川大学学报(工程科学版), 2008,40(2): 38-43.

[26] 朱 嵩,刘国华,王立忠.水动力-水质耦合模型污染源识别的贝叶斯方法 [J]. 四川大学学报(工程科学版), 2009,41(5):30-35.

[27] 毛 星.基于贝叶斯理论的事故场景重建技术 [D]. 天津:南开大学, 2009.

[28] 陈海洋,滕彦国,王金生.基于Bayesian-MCMC方法的水体污染识别反问题 [J]. 湖南大学学报(自然科学版), 2012,39(6):74- 78.

[29] 曹小群,宋君强,张卫民.对流-扩散方程源项识别反问题的MCMC方法 [J]. 水动力学研究与进展A辑, 2010,25(2):127- 136.

[30] Wei G, Chi Z, Yu L, et al. Source identification of sudden contamination based on the parameter uncertainty analysis [J]. Journal of Hydroinformatics, 2016,18(6):919-927.

[31] Thomann R V, Mueller J A. Principal of surface water quality modelling and control [M]. Prentice Hall, 1987.

[32] 谢更新.水环境中的不确定性理论与方法研究—以三峡水库为例 [D]. 长沙:湖南大学, 2005.

[33] Runkel R L. One-dimensional transport with inflow and storage (OTIS): a solute transport model for streams and rivers [M/OL]. Water-Resource Investigations Report, 1998.

[34] Scales J A, Tenorio L. Prior information and uncertainty in inverse problems [J]. Geophysics, 2001,66(2):389-397.

[35] Ntzoufras I. Bayesian modeling using WinBUGS [M]. Hoboken, New Jersey: John Wiley&Sons, 2009.

[36] Keats A, Yee E, Lien F-S. Bayesian inference for source determination with applications to complex urban environment [J]. Atmospheric Environment, 2007,41(3):465-479.

[37] Keats A, Yee E, Lien F S. Information-driven receptor placement for contaminant source determination [J]. Environmental Modelling & Software, 2010,25(9):1000-1013.

[38] Box G E P, Cox D R. An Analysis of Transformations [J]. Journal of the Royal Statistical Society, 1964,26(2):211-252.

[39] Metropolis N, Rosenbluth A W, Rosenbluth M N, et al. Equation of state calculations by fast computing machines [J]. Journal of Chemical Physics, 1953,21(10):87-92.

[40] Hasting W K. Monte Carlo sampling methods using Markov chains and their applications [J]. Biometrika, 1970,57(1):97-109.

[41] Geman S, Geman D. Stochastic relaxtion, Gibbs distirubtions and the Bayesian restoration of images [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1984,6:721-741.

[42] Liu J S. Monte Carlo Strategies in Scientific Computing [M]. New York: Springer-Verlag, 2001.

[43] Haario H, Saksman E, Tamminen J. An adaptive Metropolis algorithm [J]. Bernoulli, 2001,7(2):223-242.

[44] Haario H, Saksman E, Tamminen J. Componentwise adaptation for high dimensional MCMC [J]. Computational Statistics, 2005,20(2):265-273.

[45] Cowles M K, Carlin B P. Markov chain Monte Carlo convergence diagnostics: a comparative review [J]. Journal of the American Statistical Association, 1996,91(434):883-904.

[46] Rathbun R E, Shultz D J, Stephens D W. Preliminary experiments with a modified tracer technique for measuring stream reaeration coefficients [M/OL]. USGS Open-File Report, 1975. http: //pubs.er.usgs.gov/publication/ofr75256.

[47] Crompton J. Traveltime Data for the Truckee River Between Tahoe City, California, and Vista, Nevada, 2006 and 2007. USGS OFR 2008-1084 [M]. 2008.

[48] Rivord J, Saito L, Miller G, et al. Modeling Contaminant Spills in a Regulated River in the Western United States [J]. Journal of Water Resources Planning and Management, 2014,140(3): 343-354.

[49] Reid S E, Mackinnon P A, Elliot T. Direct measurements of reaeration rates using noble gas tracers in the River Lagan, Northern Ireland [J]. Water and Environment Journal, 2007, 21(3):182-191.

[50] Efron B. Why Isn't Everyone a Bayesian? [J]. The American Statistician, 1986,40(1):1-5.

[51] Lindley D V. The Future of Statistics: A Bayesian 21st Century [J]. Advances in Applied Probability, 1975:7.

[52] Efron B. Bayesian inference and the parametric bootstrap [J]. The Annals of Applied Statistics, 2012,6(4):1971-1997.

致谢：感谢新南威尔士大学Ashish Sharma教授对论文的指导, 感谢莫纳什大学马来西亚分校邱顺添教授对论文英文部分的审阅和修订.

Applicability of Bayesian inference approach for pollution source identification of river chemical spills: A tracer experiment based analysis of algorithmic parameters, impacts and comparison with Frequentist approaches.

JIANG Ji-ping1,2*, DONG Fu-jia1, LIU Ren-tao1, YUAN Yi-xing1

(1.School of Environment, Harbin Institute of Technology, Harbin 150090, China；2.School of Environmental Science and Engineering, Southern University of Science and Technology, Shenzhen 518055, China)., 2017,37(10)：3813~3825

Based on Bayes theorem and combined variance assumptions on pollutant concentration time series with Adaptive-Metropolis sampling, a modular Bayesian approach was established targeting at pollutant source identification during spills. This probability approach updated the prior knowledge on source information by combining experiments and monitoring and was able to directly characterize uncertainty due to the inversion process by probability distribution. Source inversion test results from field tracer experiments were investigated to determine the validity of this Bayesian inference approach, correlation of posterior parameter and impact factors. Results indicate that Bayesian approach was successful in identifying the source parameters and could effectively reduce the emergency decision risks. It is shown that the skewness of posterior distribution of source parameters and variation were sensitive to assumed variance. Using RMSE as objective function, test results also suggested that the default parameters for the established Bayesian source inversion method, were as follows: heteroscedasticity setting stabilization factors λ1= 0, and λ2= 0.1-0.5, and AM sampling proposal scale factor sd=0.1-0.3. Comparisons between the Bayesian approach and optimization approach on aspects of solution methodology, computing process and inverse results were made and differentiation were highlighted. This work provides valuable references for the practical usage of Bayesian approach in surface water pollution source identification.

Bayesian inference；source inversion；river chemical spill；Adaptive-Metropolis sampling；river tracer experiments

X52

A

1000-6923(2017)10-3813-13

姜继平(1986-),男,浙江金华人,讲师,博士,主要从事环境数学模型与决策支持系统方向研究.发表论文30余篇.

2017-03-07

国家水体污染控制与治理科技重大专项基金(2012ZX07205-005);中国博士后科学基金(2014M551249)

* 责任作者, 讲师, jjp_lab@sina.com