中等间距并列双钝体箱梁气动干扰效应试验
2017-11-07刘小兵李少杰张胜斌刘庆宽
刘小兵, 李少杰, 张胜斌, 杨 群, 刘庆宽
(1.石家庄铁道大学大型结构健康诊断与控制研究所 石家庄,050043)(2.石家庄铁道大学土木工程学院 石家庄,050043)(3.河北省大型结构健康诊断与控制重点实验室 石家庄,050043)
10.16450/j.cnki.issn.1004-6801.2017.05.029
中等间距并列双钝体箱梁气动干扰效应试验
刘小兵1,3, 李少杰3, 张胜斌3, 杨 群3, 刘庆宽1,3
(1.石家庄铁道大学大型结构健康诊断与控制研究所 石家庄,050043)(2.石家庄铁道大学土木工程学院 石家庄,050043)(3.河北省大型结构健康诊断与控制重点实验室 石家庄,050043)
通过节段模型风洞试验研究了中等间距并列双钝体箱梁的气动干扰效应,分析了气动干扰对上下游箱梁三分力系数和涡振的影响。三分力系数试验风攻角的变化范围为-10~10°,双箱梁模型的净间距与单箱梁模型宽之比D/B的变化范围为0.4~1.0。涡振试验风攻角的变化范围为-4~4°,D/B为0.8。研究结果显示:气动干扰对三分力系数的影响主要表现为对下游箱梁的影响,且体现为减小效应;在水平与负攻角来流条件下,气动干扰对上游箱梁涡振的影响较小,对下游箱梁涡振有显著的放大效应;在正攻角来流条件下,气动干扰效应对下游箱梁涡振的影响较小,对上游箱梁涡振有显著的抑制效应。
并列双钝体箱梁; 气动干扰; 风洞试验; 中等间距
引 言
目前,有关并列双钝体箱梁桥气动干扰效应的研究文献不多。林志兴等[10]在对日本矢田川三跨连续钝体钢箱梁桥进行抗风性能研究时发现,采用中央开槽(即两箱梁完全分离)方案,无论是均匀流场还是紊流场,均会出现比较明显的涡激共振现象。曲慧等[11]通过风洞试验研究了崇启大桥并列双钝体箱梁的气动干扰效应对静力系数的影响,研究表明,由于上游箱梁的遮挡,下游箱梁的阻力系数会明显减小。廖海黎等[12]通过风洞试验研究了崇启大桥并列双箱梁的涡振特性,研究发现,分离双箱梁的涡激响应存在两个涡振区,分别对应上风侧主梁的涡激响应和下风侧主梁的涡激响应。郭春平等[13]以三水河大桥为背景,数值计算了并列双钝体箱梁的静力系数,结果显示,与单幅箱梁相比,下游箱梁的阻力系数和升力系数有所降低。
综上所述,目前并列双钝体箱梁气动干扰效应的研究工作相对较少,且主要是以特定的工程为对象进行抗风研究,参数的变化不多。为了深化对并列双钝体箱梁气动干扰规律的认识,指导实际工程中大跨度并列双钝体箱梁桥的抗风设计,十分有必要展开进一步的深入研究。
1 试验简介
风洞试验在石家庄铁道大学大气边界层风洞中进行,试验流场为均匀流场。以国内某座并列双钝体箱梁桥为工程背景,根据其主跨跨中断面设计制作节段试验模型,模型的几何缩尺比为1∶32。模型的尺寸如图1所示,单幅模型的长度L为2 000 mm,宽度B为370 mm,高度H为110 mm。在上下游模型的中央位置沿周向各布置60个测压孔,考虑到模型尖角处流动参数变化幅度较大,这些位置的测点布置相对较密集。模型表面不同位置测压孔的风压通过电子压力扫描阀测得,电子压力扫描阀的采样频率为330 Hz。单箱梁模型及并列双箱梁的三分力系数测试装置如图2所示,模型刚性悬挂,作用在模型上的三分力可通过对模型表面各测点的压力进行积分得到。单箱梁模型及并列双箱梁模型的涡激振动测试装置如图3所示,模型弹性悬挂,试验参数见表1。模型的振动位移通过激光位移计测得,振动过程中模型表面各测点的动态压力时程通过电子压力扫描阀测得。如图1所示,定义斜向上吹向模型的来流风为正攻角来流风,斜向下吹向模型的来流风为负攻角来流风。
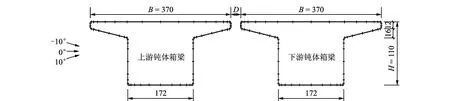
图1 并列双箱梁模型的尺寸及测点布置(单位:mm)Fig.1 Geometry parameters and tap arrangements oftwin parallel box girders with bluff body (unit: mm)

图2 三分力系数测试装置Fig.2 Testing set-up of aerodynamic coefficients

图3 涡激振动试验装置Fig.3 Testing set-up of vortex-induced vibration

模型位置m/kgf/Hz阻尼比/%竖弯频率fh扭转频率fα竖弯阻尼比ξh扭转阻尼比ξα上游钝体箱梁模型19.215.6010.480.910.59下游钝体箱梁模型19.365.5810.270.860.63
基于刚性悬挂节段模型风洞试验分别测试了-10~10°的风攻角范围内单幅钝体箱梁的三分力系数,以及双钝体箱梁在15个不同间距下的三分力系数。双箱梁模型的净间距D与单箱梁模型宽B之比D/B的变化范围为0.025~6。为了便于讨论,将D/B小于0.4和大于1的间距分别定义为小间距和大间距、D/B界于0.4和1的间距定义为中等间距。基于弹性悬挂节段模型风洞试验,测试了-4~4°的风攻角范围内单幅钝体箱梁的涡振特性,以及并列双钝体箱梁在D/B=0.1(小间距)、D/B=0.8(中等间距)和D/B=3(大间距)三个不同间距下的涡振特性。限于篇幅,笔者主要讨论中等间距并列双钝体箱梁的气动干扰效应,分析这种气动干扰对三分力系数和涡振的影响。
2 气动干扰对三分力系数的影响
2.1 并列双钝体箱梁的三分力系数
单箱梁的三分力可用无量纲的三分力系数来表征。三分力系数定义如下
阻力系数CD=2FD/ρU2B
(1)
升力系数CL=2FL/ρU2B
(2)
扭矩系数CM=2MT/ρU2B2
(3)
其中:B为单箱梁模型的宽度;U为来流风速;ρ为空气密度;FD,FL和MT分别为风轴坐标系下单箱梁模型单位长度上的顺风向阻力、横风向升力及绕中心的扭矩。
3.1 护士主观幸福感及婚姻质量现状 调查结果显示,护士主观幸福感总得分平均为(86.35+10.04)分,护士的婚姻质量总得分平均为(427.01+33.89)分。根据得分在73~96分为主观幸福感较高[6]作为标准,得出本研究纳入对象的主观幸福感总体水平良好。这可能是因为已婚护士家庭结构稳定,多数已具有一定的事业、经济基础,熟悉医院医疗工作环境,收入固定,比较满足现状,所以较能安心于本职工作。这与陆彩萍等[7]的研究结果相一致。
三分力的正方向定义如图4所示。
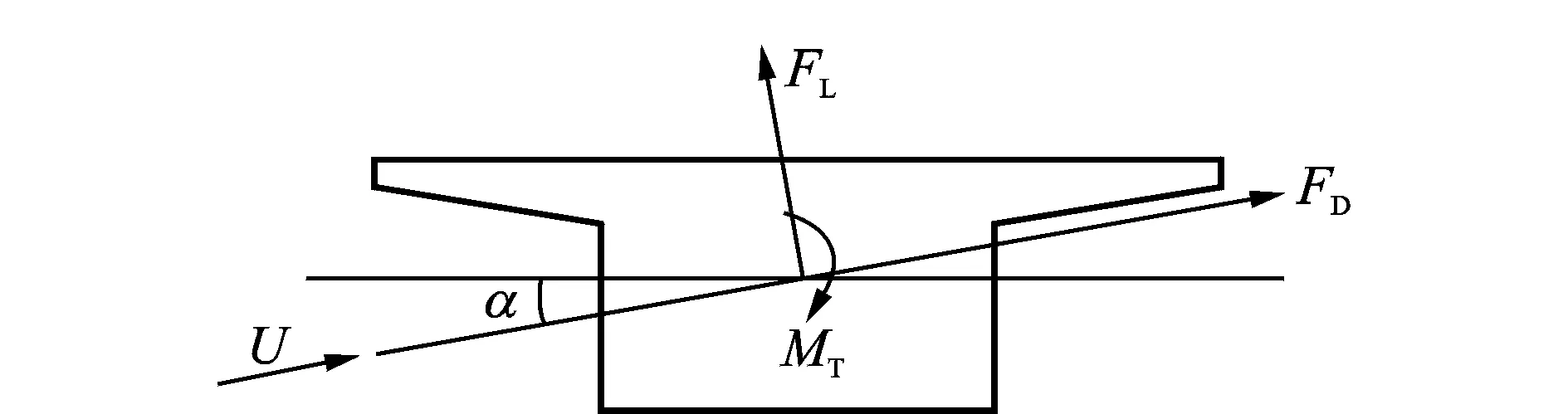
图4 单箱梁模型的三分力示意Fig.4 Illustration of aerodynamic forces of single box girder model
图5显示了单箱梁及并列双箱梁在D/B=0.8时的三分力系数随风攻角的变化曲线。限于篇幅,其他间距下并列双箱梁的三分力系数没有给出。可以看到,单箱梁的阻力系数和扭矩系数随攻角的变化比较平缓,升力系数随攻角的变化比较剧烈。
从整体上看,与单箱梁的三分力系数相比,上游箱梁的三分力系数变化很小,下游箱梁的三分力系数变化较大。这种变化不仅体现在随攻角的变化趋势上,也表现在每个攻角下的具体数值上。
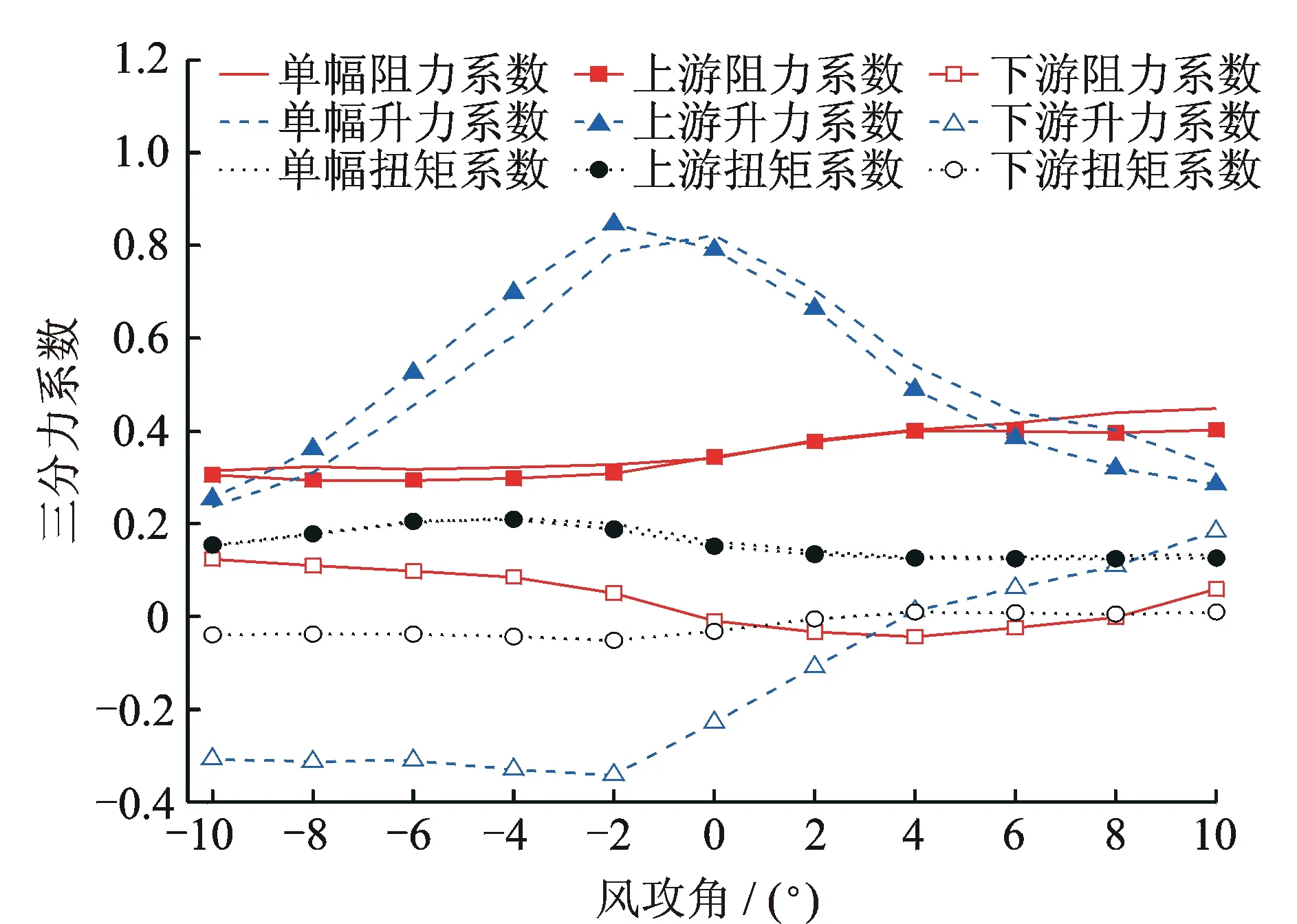
图5 单箱梁及双箱梁(D/B=0.8)的三分力系数随风攻角的变化曲线Fig.5 Variation of aerodynamic coefficients of single and twin box girder with wind attacking angles
2.2 下游钝体箱梁的三分力系数干扰因子
为了定量地评价气动干扰效应对下游箱梁三分力系数的影响,定义如下干扰因子

(4)
从以上定义可以看到:干扰因子大于1,表示气动干扰对下游箱梁三分力系数的增大效应;干扰因子小于1,表示气动干扰对下游箱梁三分力系数的减小效应。
图6给出了下游箱梁的三分力系数干扰因子随风攻角和无量纲间距D/B的变化云图。可以看到:a.阻力系数干扰因子的变化范围约为-0.25~0.55左右,随着间距的变小,阻力系数干扰因子呈现出逐渐减小的变化规律,随着攻角的增大,阻力系数干扰因子大体呈现出先减小后增大的变化规律,在4°攻角左右干扰因子最小;b.升力系数干扰因子的变化范围约为-1.7~0.7左右。同一攻角下,升力系数干扰因子基本不随间距的变化而变化,同一间距下,升力系数干扰因子随着攻角的变小而变小;c.扭矩系数干扰因子的变化范围约为-0.5~0.4左右。随着攻角和间距的变小,扭矩系数干扰因子呈现出逐渐减小的变化规律。

图6 下游箱梁的三分力系数干扰因子云图Fig.6 IF contour of aerodynamic coefficient of leeward box girder
以上分析表明,中等间距并列双钝体箱梁的气动干扰效应对下游箱梁三分力系数有较大的影响,且表现为减小效应。对阻力系数而言,间距越小,减小效应越明显,与其他攻角相比,4°攻角左右时的减小效应更明显;对升力系数而言,减小效应对间距不敏感,攻角越小,减小效应越显著。对扭矩系数而言,攻角和间距越小,减小效应越显著。
文中下游钝体箱梁的三分力系数干扰因子与刘志文等[8]得到的分离双扁平箱梁下游箱梁的三分力系数干扰因子存在较大差别。以阻力系数干扰因子为例,在大体接近的无量纲间距D/B情况下,下游钝体箱梁阻力系数干扰因子明显小很多。笔者认为,这种差异源于箱梁断面的外形差异。与扁平箱梁相比,钝体箱梁的高度更大,因此,上游钝体箱梁对下游钝体箱梁的遮挡效应更显著。
3 气动干扰对涡振的影响
由于涡激振动试验中没有观测到明显的扭转涡振,以下仅讨论气动干扰效应对并列双钝体箱梁竖向涡激振动的影响。

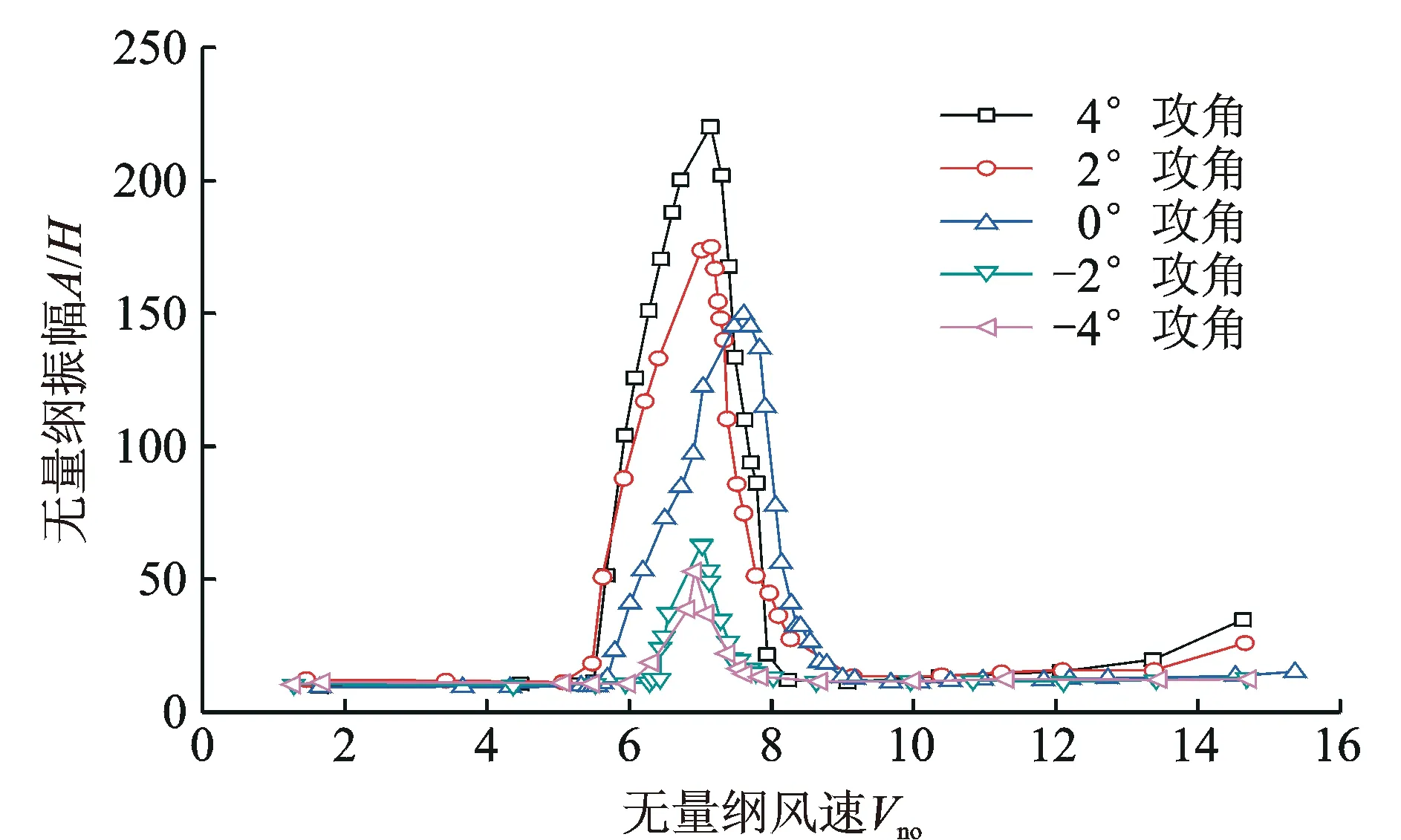
图7 单箱梁的无量纲竖向振幅随无量纲风速的变化曲线Fig.7 Variation of vertical vibration amplitude of single box girder with wind speed
风洞试验观测到,并列双钝体箱梁也发生了竖向涡激振动,上下游箱梁的振动频率相同,均接近竖向固有频率,上下游箱梁的振动并不同步,存在一定的相位差。上下游箱梁的涡振锁定区间、振幅及相位差随着风攻角的变化而变化。

图8 双箱梁(D/B=0.8)的无量纲竖向振幅随无量纲风速的变化曲线Fig.8 Variation of vertical vibration amplitude of twin box girder(D/B=0.8)with wind speed
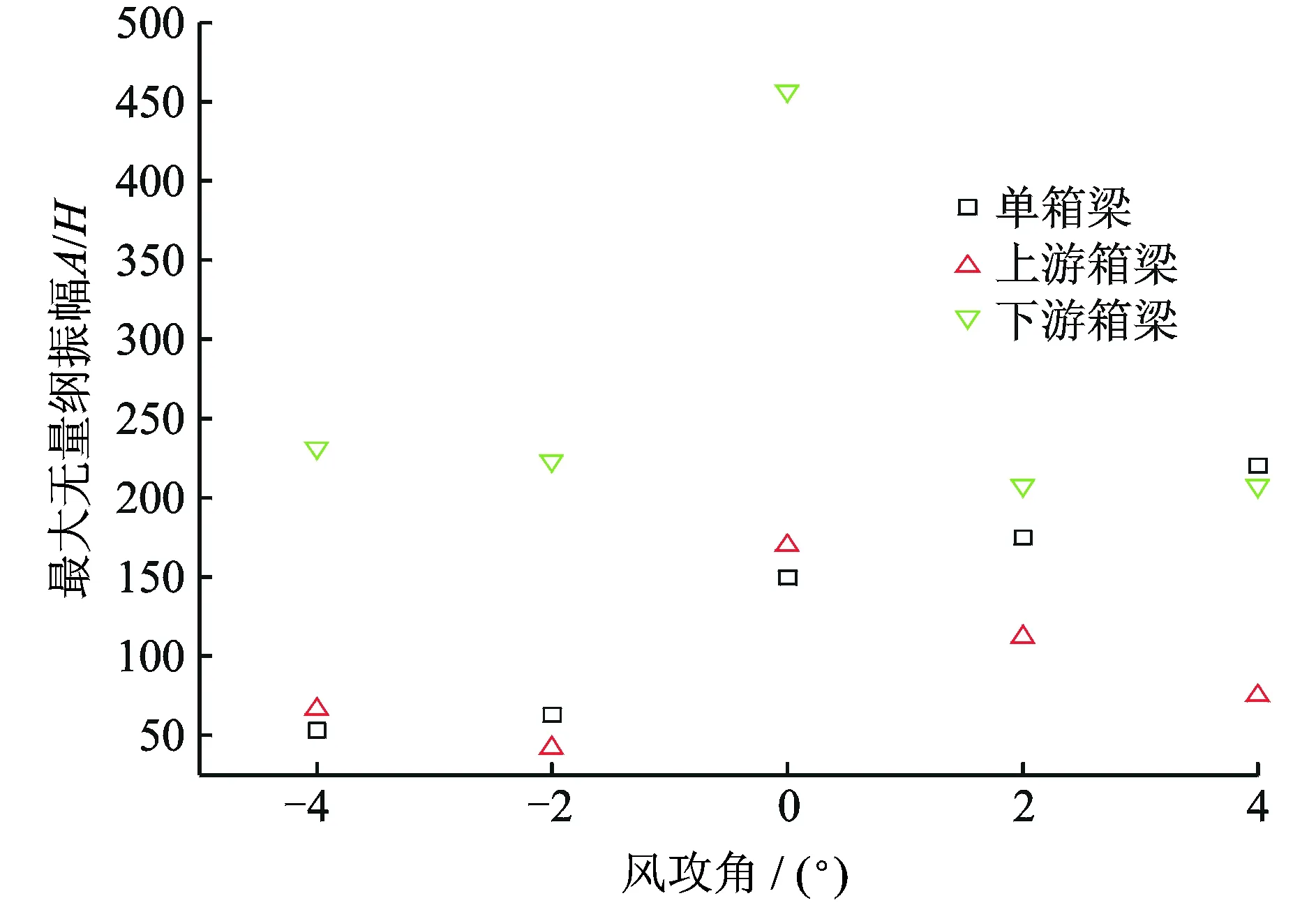
图9 单箱梁与双箱梁的最大无量纲竖向振幅对比Fig.9 Comparison of maximum vertical vibration amplitude of single box girder and twin box girder
图8显示了不同攻角并列双钝体箱梁在D/B=0.8时的无量纲竖向振幅随无量纲风速的变化曲线。图中振幅和风速的无量纲化方式与图7中单箱梁振幅和风速的无量纲化方式一致。为了方便分析气动干扰对涡振的影响,图9显示了不同攻角上下游箱梁的最大振幅,并与单箱梁的最大振幅进行了对比。从图9可以看到,在-4~0°的风攻角范围,上游箱梁与单箱梁的最大振幅大体接近。下游箱梁的最大振幅明显大于单箱梁的最大振幅。在-4,-2和0°风攻角下,下游箱梁的最大振幅分别为单箱梁最大振幅的4.4倍、3.5倍和3.1倍左右。在2°和4°两个正向风攻角下,下游箱梁和单箱梁的最大振幅大体接近。上游箱梁的最大振幅明显小于单箱梁的最大振幅。2°和4°风攻角下,上游箱梁的最大振幅分别仅为单箱梁最大振幅的64%和34%左右。
以上分析表明,在水平与负攻角来流条件下,并列双钝体箱梁的气动干扰对上游箱梁涡振的影响较小,对下游箱梁涡振有显著的放大效应,攻角绝对值越大,放大效应越明显。在正攻角来流条件下,并列双钝体箱梁的气动干扰对下游箱梁涡振的影响较小,对上游箱梁涡振有显著的抑制效应,攻角越大,抑制效应越明显。
4 结 论
1) 当0.4≤D/B≤1(D为双箱梁模型的净间距,B为单箱梁模型宽),风攻角为-10~10°时,并列双钝体箱梁的气动干扰对上游箱梁三分力系数的影响基本可以忽略,对下游箱梁三分力系数有较大的影响,且表现为减小效应。对阻力系数而言,间距越小,减小效应越明显,与其他攻角相比,4°攻角左右时的减小效应更明显;对升力系数而言,减小效应对间距不敏感,攻角越小,减小效应越显著。对扭矩系数而言,攻角和间距越小,减小效应越显著。
2) 当D/B=0.8,风攻角为-4~4°时,在水平与负攻角来流条件下,并列双钝体箱梁的气动干扰对上游箱梁涡振的影响较小,对下游箱梁的涡振有显著的放大效应,攻角绝对值越大,放大效应越明显。在正攻角来流条件下,并列双钝体箱梁的气动干扰对下游箱梁涡振的影响较小,对上游箱梁的涡振有显著的抑制效应,攻角越大,抑制效应越明显。
[1] Seo J, Kim H, Park J, et al.Interference effect on vortex-induced vibration in a parallel twin cable-stayed bridge[J].Journal of Wind Engineering and Industrial Aerodynamics,2013,116: 7-20.
[2] Kimura K, Shima K, Sano K, et al. Effects of seperation distance on wind-induced response of parallel box girders[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96: 954-962.
[3] Laima S, Hui L. Effects of gap width on flow motions around twin-box girders and vortex-induced vibrations[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 139: 37-49.
[4] Kwok K, Qin X, Fok C, et al. Wind-induced pressures around a sectional twin-deck bridge model: Effects of gap-width on the aerodynamic forces and vortex shedding mechanisms[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2012, 110: 50-61.
[5] 朱乐东, 周奇, 郭震山, 等. 箱形双幅桥气动干扰效应对颤振和涡振的影响[J]. 同济大学学报, 2010, 38(5): 632-638.
Zhu Ledong, Zhou Qi, Guo Zhenshan, et al. Aerodynamic interference effects on flutter and vortex-excited resonance of bridges with twin-separate parallel box decks[J]. Journal of Tongji University, 2010, 38(5): 632-638. (in Chinese)
[6] 郭震山, 孟晓亮, 周奇, 等.既有桥梁对邻近新建桥梁三分力系数的气动干扰效应[J]. 工程力学,2010,27(9):181-186.
Guo Zhenshan, Meng Xiaoliang Zhou Qi, et al. Aerodynamic interferences of an existed bridge on aerodynamic coefficients of an adjacent new bridge[J]. Engineering Mechanics, 2010, 27(9): 181-186. (in Chinese)
[7] 陈政清, 牛华伟, 刘志文. 双幅桥面桥梁主梁气动干扰效应研究[J]. 桥梁建设, 2007(6): 9-12.
Chen Zhengqing, Niu Huawei, Liu Zhiwen. Study of aerodynamic interference effect on main girders of twin-deck bridges [J]. Bridge Construction, 2007(6): 9-12. (in Chinese)
[8] 刘志文, 陈政清, 刘高. 双幅桥面桥梁三分力系数气动干扰效应试验研究[J]. 湖南大学学报, 2008, 35(1): 16-20.
Liu Zhiwen, Chen Zhengqing, Liu Gao. Experimental study of aerodynamic interference effects on aerostatic coefficients of twin decks bridges [J]. Journal of Hunan University, 2008, 35(1): 16-20. (in Chinese)
[9] 陈政清, 刘小兵, 刘志文. 双幅桥面桥梁三分力系数的气动干扰效应研究[J]. 工程力学, 2008, 25(7): 87-93.
Chen Zhengqing, Liu Xiaobing, Liu Zhiwen. Study of aerodynamic interference effects on aerodynamic coefficients of twin-deck bridges[J]. Engineering Mechanics, 2008, 25(7): 87-93. (in Chinese)
[10] 林志兴,葛耀君,曹丰产,等.钢箱梁桥的抗风问题及其对策研究[J].同济大学学报,2002,30(5):614-617.
Lin Zhixing, Ge Yaojun, Cao Fengchan, et al. Wind resistant study and prevention research of steel box girder[J]. Journal of Tongji University, 2002, 30(5): 614-617. (in Chinese)
[11] 曲慧, 马如进, 陈艾荣. 分离式钝体钢箱梁静气动力节段风洞试验研究[J]. 结构工程师,2010,26(3): 89-94.
Qu Hui, Ma Rujin, Chen Airong. Study on static aerodynamic force of separate steel box-girder with bluff body via wind tunnel test of sectional model[J]. Structural Engineers, 2010, 26(3): 89-94. (in Chinese)
[12] 秦浩, 廖海黎, 李明水. 大跨度双幅连续钢箱梁桥涡激振动特性风洞试验研究[J]. 振动与冲击, 2014, 33(14): 206-210.
Qin Hao, Liao Haili, Li Mingshui. Vortex induced vibration performance of long span continuous steel twin box beam bridge based on wind tunnel test[J]. Journal of Vibration and Shock, 2014, 33(14):206-210. (in Chinese)
[13] 郭春平, 白桦, 洪光. 双幅桥静分力系数气动干扰效应研究[J]. 重庆交通大学学报:自然科学版, 2011,30(5): 899-902.
Guo Chunping, Bai Hua, Hong Guang. Effects of aerodynamic interference on aerodynamic coefficients of twin-deck bridges[J]. Journal of Chongqing Jiaotong University: Natural Science, 2011,30(5): 899-902. (in Chinese)
国家自然科学基金资助项目(51308359,51378323);河北省高等学校科学技术研究基金资助项目(QN20131169,QN2015213)
2016-12-11;
2017-03-03
TU311; TH113

刘小兵,男,1982年3月生,博士、副教授。主要研究方向为桥梁结构的风荷载与风致振动研究。曾发表《双幅桥面桥梁三分力系数的气动干扰效应研究》(《工程力学》2008年第25卷第7期)等论文。
E-mail:x_b_liu@126.com
