一种基于Viterbi法的改进瞬时转速估计算法

2017-11-07刘永强郝高岩廖英英杨绍普

振动、测试与诊断 2017年5期

关键词：阶次时频代价

刘永强，郝高岩，廖英英，杨绍普

(1.石家庄铁道大学机械工程学院石家庄，050043)(2.石家庄铁道大学土木工程学院石家庄，050043)

10.16450/j.cnki.issn.1004-6801.2017.05.025

一种基于Viterbi法的改进瞬时转速估计算法

刘永强1，郝高岩1，廖英英3，杨绍普1

(1.石家庄铁道大学机械工程学院石家庄，050043)(2.石家庄铁道大学土木工程学院石家庄，050043)

针对无转速计的瞬时转速估计问题及现有方法在抗噪、抗临近阶次和实时性方面的不足，基于Viterbi算法提出了一种改进型瞬时频率估计(instantaneous frequency estimation,简称IFE)方法，并将其应用于变转速工况下滚动轴承的瞬时转速估计。将隐马尔科夫模型中的Viterbi算法引入转频估计，分析了某一时频平面中代价函数的计算次数；根据欧几里得距离函数的性质，提出了代价函数迭代循环停止的新型判定准则。该准则的优点在于可以快速搜索时频平面，寻找到最优的局部路径，提高了IFE精度和计算速度。通过仿真信号和实验数据对该算法进行验证。结果表明：改进后算法效率明显提高，和基于峰值搜索IFE方法相比，改进的Viterbi-IFE方法具有较高的精度和稳定性。

滚动轴承；振动信号；瞬时频率估计； Viterbi算法；代价函数

引言

阶次分析为变转速工况下滚动轴承故障诊断的重要方法之一[1]，该方法中的关键问题就是准确追踪参考轴转速。一般情况下可采用转速计等硬件装置测量转速，但在某些复杂工况下转速计等键相装置不易安装，难以跟踪参考轴转速。针对该问题本研究改进了瞬时频率估计方法，从测量的振动信号中提取出转频信息，继而实现无需转速计的阶次分析。

陈平等[2]研究了基于MUSIC的瞬时频率估计方法，但存在相位重叠且只适用于单分量信号；为实现无转速计的阶次跟踪，郭瑜等[3-5]提出对采集的振动信号进行短时傅里叶变换得到时-频图，再通过局部峰值搜索获得瞬时频率(instantaneous frequency,简称IF)，但该方法的抗噪性及抗临近阶次的能力不足；赵晓平等[6-7]提出基于Viterbi算法的瞬时频率估计方法，但由于该算法较复杂，运算时间较长，无法满足实时分析的要求。Leclere等[8]提出了一种瞬时转速估计算法，不需要进行先验假设，而是由信号瞬时谱产生的概率密度函数来确定转速信息。基于瞬时时间尺度因子估计，Combet等[9]提出了一种瞬时转速相对波动估计方法，该方法采用峭度最大值法获得分析信号的最佳长度，基于短时尺度变换估计瞬时转速信息。Urbanek等[10]基于相空间重构和时频分析，提出一种两步法用于估计瞬时频率，可处理剧烈波动的转速或复杂谱特征信号，但这些算法大多对抗临近阶次和实时性方面没有过多要求。

针对目前算法的不足，笔者研究了Viterbi算法的路径寻优过程及其迭代次数，改进了该算法的寻优方法，并提出了迭代循环停止的新型判定准则。改进后的方法提高了瞬时频率的估算精度和计算速度，为实现无转速计的实时阶次跟踪打下基础。

1 基于Viterbi算法IFE的理论基础

Viterbi算法是针对隐马尔科夫模型提出的[11]：给出一个观测序列O1，O2，O3，…，希望找到观测序列背后的隐藏状态序列P1，P2，P3，…，可采用动态规划的方法来寻找出现概率最大的隐藏状态序列。

基于Viterbi算法的IFE方法的基本思想来源于数字图像处理中的边线追踪(edge-following)算法[12]，其原理是连接地图(时频平面)上的点，使这些点形成的路径的长度值和高度变化值之和尽可能小，这和隐马尔科夫模型中寻找观测序列背后最可能的隐藏状态序列相同[13]。

在一个由N组时间点和M组频率点组成的时频网格中，求出从第一组时间点到最后一组时间点的最优路径。设相邻时间点n1，n2之间的所有路径集合为K。n1，n2之间的最佳路径表达式为

(1)

其中：p(k(n);n1,n2)为沿路径k(n)的代价函数，其为g(x,y)和f(x)之和，时间从n1到n2；函数g(x,y)=g(|x-y|)为关于|x-y|的非增函数，其中x和y分别为路径k(n)和k(n-1)所处的网格位置频率编号，则g(x,y)表示x、y两个连续时间点之间的距离；f(x)为关于x=Sf(n,k(n))的非减函数，其中函数Sf(x,y)为短时傅里叶变换(shorttimeFouriertransformation,简称STFT)后所得时频平面的幅值。

通过这样的定义，时频平面中的频率点所对应的STFT值越大，其成为瞬时频率估计点的概率就越大。函数f(x)定义如下：考虑时刻n，把该时刻的STFT值Sf(n,w)按从大到小的顺序排列

Sf(n,ω1)≥Sf(n,ω2)≥…≥Sf(n,ωj)≥

…≥Sf(n,ωM)

(2)

其中：j∈[1,M]，M为信号频率点数。

f(x)定义为f(Sf(n,ωj))=j-1，该定义使IFE值第j个最大值的概率随着j的增大而线性降低，可保证Sf(n,w)的较大者作为估计结果[14]。

下面对g(x,y)的形式进行讨论。假设信号在持续时间范围内IF值没有发生突变，可将g(x,y)的形式表达为

(3)

若整个信号持续时间范围内IF有突变点，g(x,y)的形式为

(4)

分析式(3)，(4)，当两连续时间点的IF变化小于Δ1，此时距离函数g(x,y)为零，没有距离函数引起的代价。当Δ1→∞时，此时g(x,y)恒为零，估计结果为STFT的最大值。当两连续点的瞬时频率有突变时，即|x-y|>Δ2，g(x,y)=c(Δ2-Δ1)，此时g(x,y)不为|x-y|的函数，而为定值c(Δ2-Δ1)，将距离函数限制在一定范围内，准确追踪到突变点。另外，c和Δ的选择需要根据预提取信号的波动情况而定，波动越大Δ越大。

2 基于Viterbi算法的改进

2.1 改进的迭代算法

在一个由M组频率点和Q组时间点组成的时频网格中，即T={(ni,ωj)|i∈[1,Q],j=[1,M]}，整个时频平面需要计算的路径总数为MQ，但在点数比较多的情况下，计算量非常大，实现起来难度很大。文中采用迭代方法简化计算，并提出代价函数循环停止的判定准则，改进的迭代过程如下。

1) 假设从时刻n1到时刻(ni,ωj)的最优路径Li(n,ωj)已经确定，最优路径表达式为

(5)

其中：n∈[n1,ni]；j∈[1,M]；Kij为从n1到(ni,ωj)的路径的集合；p(k(n);n1,(ni,ωj))为沿路径k(n)的代价函数，最优路径为代价函数最小的那条。

这里对于ni时刻的不同的频率点，均存在一条最优路径，共M条最优路径。则在时间段[n1,ni]中，估计的瞬时频率曲线就取M条最优路径中代价函数最小的那条。表达式为

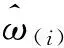
(6)

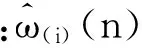
2) 迭代到下一点ni+1的局部最优路径可以表示为

Li+1(n，ωj)=[Li(n，ωl),(ni+1,ωj)]

(j∈[1,M]；l∈[1,M])

(7)

新的代价函数为

p(li+1(n,ωl);n1,(ni+1,ωj))=

p(Li(n,ωl);n1,(ni,ωj))+g(ωl,ωj)+

f(Sf(ni+1,ωj))

(8)

最优路径取代价函数值最小的路径。这里Li+1(n;ωj)对于不同频率点也存在M个局部最优路径。任一时刻均有M个频率点，计算每个频率点的局部最优路径需要计算M次，因此计算出该时刻所有点的局部最优路径共计算M2次，对于整个时频平面Q组时间点，共计算(Q-1)×M2次，远远小于之前MQ的计算量。

为了进一步减小计算量，观察代价函数表达式(8)，p(Li(n;ωl);n1,(ni,ωj))为前ni组时间点局部最优路径的代价函数，g(ωl,ωj)为欧几里得距离|ωl-ωj|的单调增函数。计算局部最优路径时，如果每组时间点中的每个频率点ωj(j∈[1,M])不变，那么所对应的函数值f(Sf(ni+1,ωj))不变。因此采用以下步骤进一步减小计算量。

①令ρ=Δ；

3) 按步骤2)计算每个频率点的局部最优路径。将该时间点的最优路径代价函数作为结果，带入下一时间点代价函数的计算中，依次迭代，求出整个时频平面的最优路径。

2.2 迭代算法仿真算例

假设由M=8和Q=3组成的时频网格的一个元素为fij=f(Sf(ni,wj))，如图1所示。

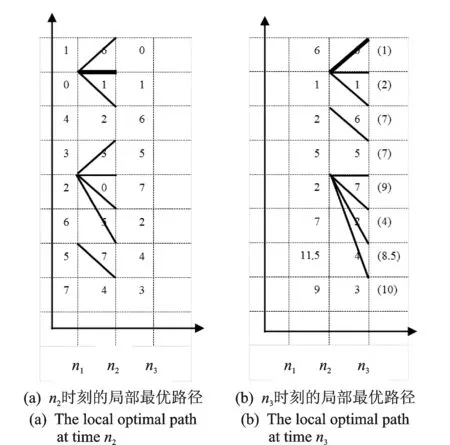
图1 M=8，Q=3迭代过程仿真算例Fig.1 Iterative process when M=8，Q=3

由式(3)计算g(ωi,ωj)=gij，其中c=2.5，Δ=1。连接某时刻的某一频率点与其前一时刻距离最近的3个频率点，即|i-j|≤1时，gij=0。当|i-j|>1时，gij=2.5×|i-j|。

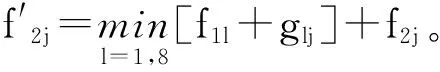
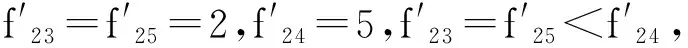
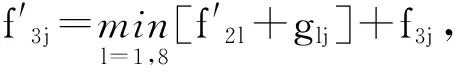
3 算法验证

3.1 线性扫频信号验证

在轴承故障诊断中，轴承振动信号为含噪声的多分量信号，经过预处理后其噪声仍然很大，且可能出现临近阶次。为检验基于Viterbi算法的IFE方法的抗噪和抗临近阶次能力，采用仿真信号进行研究，其瞬时频率如式(9)所示。

ω(t)=2.5πt+30π

(9)

通过该频率调制规律来仿真滚动轴承升速工况振动信号，其多分量信号模型[15]为

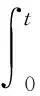
(10)

其中：η(t)为高斯白噪声；信噪比为-9 dB。

时域波形如图2所示。转频从15 Hz线性变化到40 Hz，持续时间20 s。仿真模型中包含转频的一倍频，幅值为1；0.66倍频，幅值为0.8；0.5倍频，幅值为0.7。STFT时频图如图3所示，可以观察到由于噪声影响，各倍频分量并不突出。

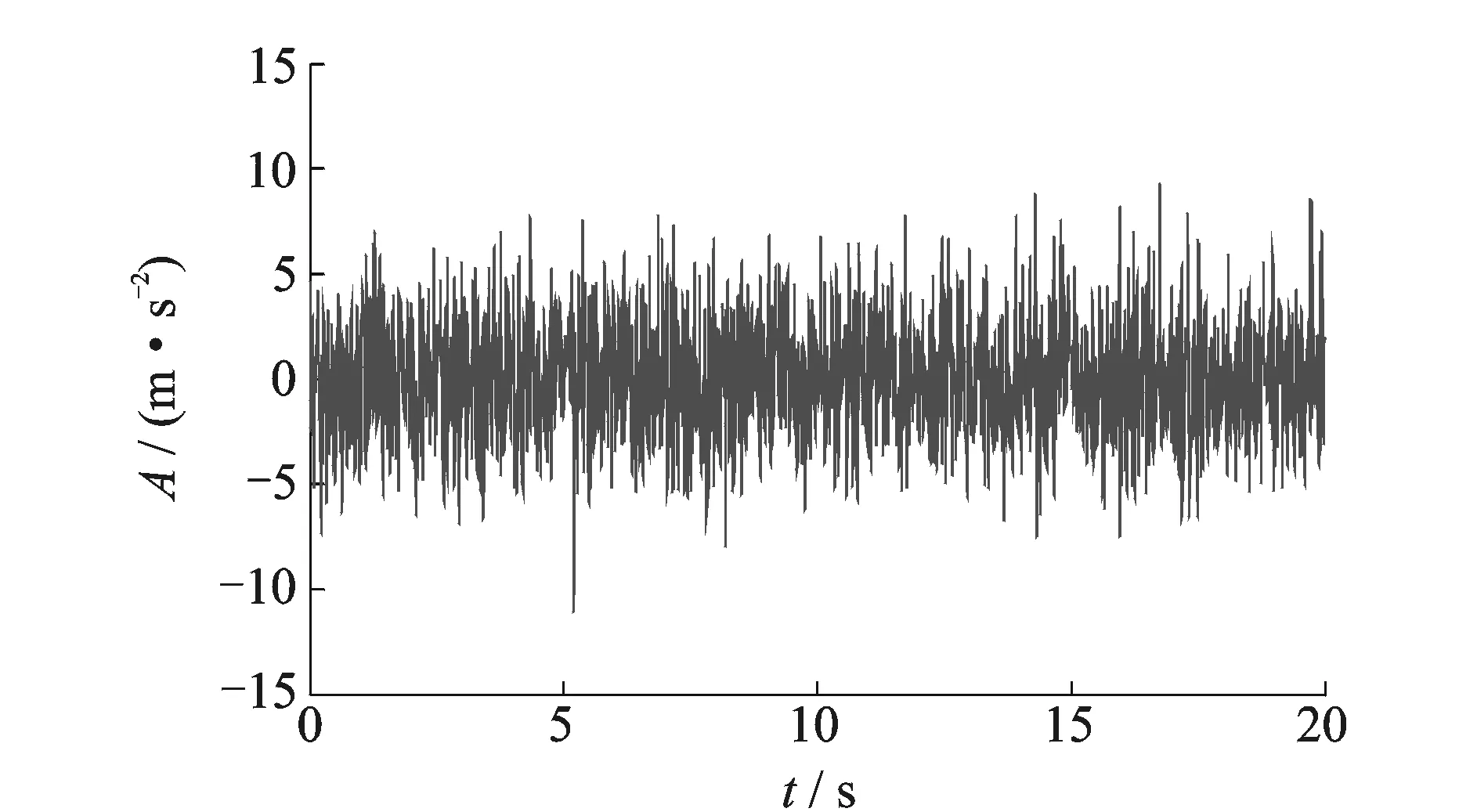
图2 线性扫频时域信号Fig.2 Linear sweep frequency signal in time domain

分别采用局部峰值搜索算法和基于Viterbi算法的IFE方法提取转频，结果如图4所示。图中星点线为基于Viterbi算法的IFE方法得到的转频曲线，短画线为局部峰值搜索法得到的转频曲线，实线为理论转频曲线。

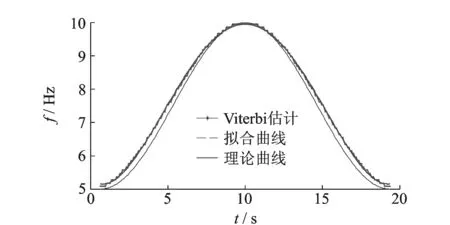
图4 线性扫频信号IFE结果对比图Fig.4 IFE results comparison for linear sweep frequency signal

根据式(11)求两种算法的瞬时频率估计值相对于理论值的百分比误差。

(11)

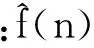
局部峰值搜索算法的误差ξ=43.4%，基于Viterbi算法的IFE误差ξ=3.11%。可以看出在高噪声和出现临近阶次的情况下，局部峰值搜索算法已经失效，抗噪和抗临近阶次的能力有限。而基于Viterbi算法的IFE结果具有很高的精度，在较高噪声干扰下仍可精确进行估计。

3.2 正弦扫频信号

仿真强噪声环境下的正弦扫频信号，并计算其相对于理论值的百分比误差。瞬时频率由式(12)给出。

ω(t)=2π(7.5-2.5cos(t))t=[0,2π]

(12)

正弦扫频信号模型如式(13)所示，其中包含1，2，4阶三个分量[15]。

(13)

其中：η(t)为高斯白噪声；信噪比为-3 dB；采样率为100 Hz。

转频呈正弦规律变化，仿真模型中包含转频的一倍频，即一阶分量，幅值为1；二阶分量，幅值为0.6；四阶分量，幅值为0.4。STFT时频谱如图5所示。

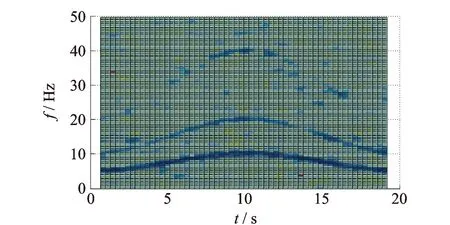
图5 正弦扫频信号STFT谱图Fig.5 STFT for sinusoidal sweep frequency signal

现采用基于Viterbi算法的IFE方法提取第一个分量，结果如图6所示。点线为采用Viterbi算法估计的瞬时频率连线；粗实线为将瞬时频率点采用5次多项式拟合得到的频率曲线；短划线为理论频率曲线。可以看到点线相对于理论值在局部存在一定误差，出现突变点，但转速通常为平稳连续变化，因此这里采用低阶多项式进行拟合，得到比较平滑的估计曲线。拟合曲线相对于理论曲线的百分比误差为ξ=3.45%，可以得出，基于Viterbi算法的IFE方法可以精确估计瞬时转频，具有较好的抗噪性和抗临近阶次的能力。

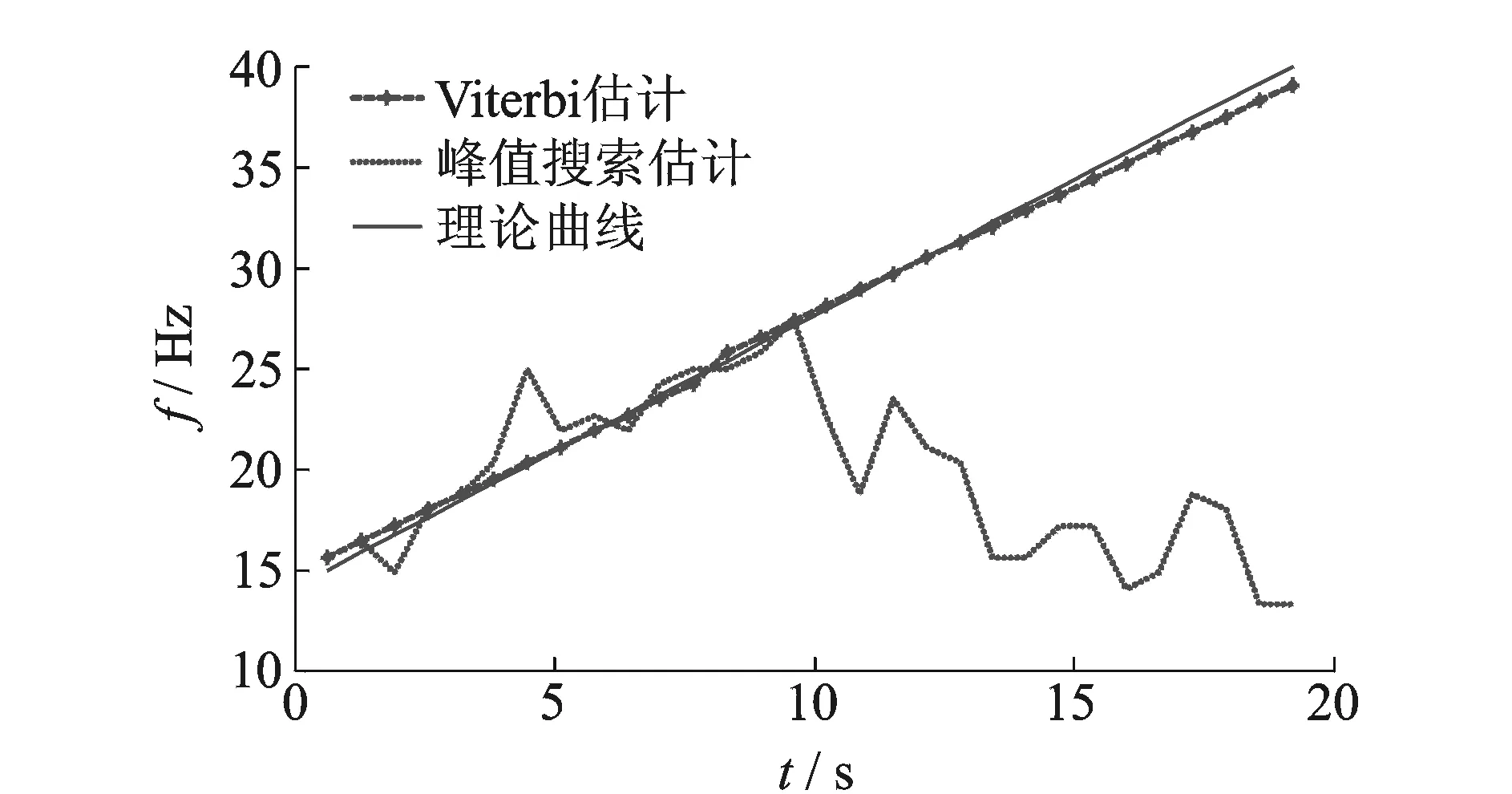
图6 正弦扫频信号IFE结果Fig.6 IFE results for sinusoidal sweep frequency signal

3.3 实验信号

采用QPZZ-Ⅱ型旋转机械振动及故障模拟实验平台进行变转速振动测试试验，实验台如图7所示。

图7 旋转机械振动及故障模拟实验台Fig.7 Test rig of rotating machinery vibration and fault simulation

实验采用NI PXIe 4496数据采集设备，采用PCB 355B03型压电加速度传感器测量振动信号，采样频率为25.6 kHz；采用PCB LaserTach ICP型激光转速传感器测量参考轴转速，采样频率为1 kHz。根据转速脉冲信号采用5点公式法[16]计算参考轴的瞬时转频，并将该方法测得的转频作为参考值。

实验中轴承节圆直径D=38.5 mm，滚子直径d=7.2 mm，滚子个数Z=13，接触角α=0。根据外圈故障特征频率计算公式，得外圈故障特征阶次为

Obpo=Z[1-d/Dcos(α)]/2≈5.284

(14)

模拟转速剧烈波动工况，原始振动信号如图8所示。根据轴承故障诊断实验平台振动信号的特点，采用共振解调方法进行故障特征提取。采集信号通过包络解调就可以得出随转速变化的低频幅值包络信号。

图8 原始时域振动信号Fig.8 Original vibration signal in time domain

为提取低频区段内的转速信息，对信号进行低通滤波和降采样处理，低通滤波截止频率设定为1 500 Hz，降采样倍数为5，降采样后的采样率为5 120 Hz。然后对降采样后的数据进行Hilbert包络并去趋势项得预处理振动信号。预处理振动信号STFT谱图如图9所示。

图9 振动信号STFT时频谱图Fig.9 STFT for the rolling bearing vibration signal

根据轴承故障特征频率计算公式可看出，故障特征阶次一倍频的峰值在时频谱图中最突出，因此将其作为搜索目标。

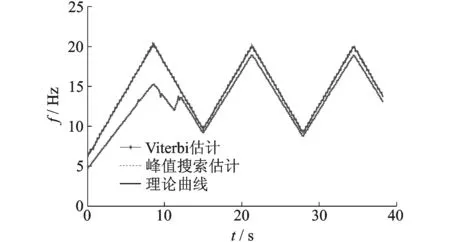
图10 Viterbi法、峰值搜索法、转速计测得结果对比图Fig.10 Comparison of the results from Viterbi-IFE、Peaksearch-IFE and the tachometer

对图9进行基于Viterbi算法的转频估计，得到估计结果，如图10所示。图中实线为采用激光转速计测量转速脉冲计算得到的参考轴瞬时频率曲线，星点线为基于Viterbi算法所估计出的转频曲线，点虚线为采用峰值搜索算法估计的转速曲线。可以看出，Viterbi-IFE和转速计测得转速曲线基本一致，而峰值搜索在局部出现较大偏差。求估计瞬时频率值相对于参考值的百分比误差，根据公式(9)计算，峰值搜索误差为8.5%，Viterbi-IFE估计误差仅为0.71%。

分别采用改进前与改进后的Viterbi算法对实验信号STFT谱图进行瞬时频率估计，其代价函数迭代过程所用时间如表1所示。计算时统一采用MATLAB编程，硬件为DELL笔记本电脑，4核Core i5处理器，主频1.80 GHz。在表1中，将式(10)所示的线性扫频信号和式(13)所示的正弦扫频信号同时考虑在内，分别采用改进前与改进后的Viterbi算法对该两组信号STFT谱图进行瞬时频率估计。从表1中可知，在仿真信号和实验信号验证中，使用相同计算资源的前提下，改进后的Viterbi算法计算效率得到明显提升。尤其是实验信号，无判定准则的Viterbi-IFE用时1.45 s，有判定准则的改进Viterbi-IFE用时降至0.52 s。整个转速变化过程持续时间为38 s，而进行转频估计的迭代计算过程用时0.52 s，从响应的及时性分析，该算法可以满足实时分析的要求。

表1 改进前后迭代计算所用时间

Tab.1 The time used for the iterative calculation before and after the improvement s

4 结束语

基于振动信号的瞬时转速估计使无转速计的轴承状态监测和故障诊断成为可能，其中基于振动信号STFT谱图的局部峰值搜索IFE方法是比较早的方法，但其抗噪性和抗临近阶次的能力有限。笔者研究了基于Viterbi算法的IFE方法，并分析了代价函数的迭代过程和次数，在此基础上，提出了代价函数迭代循环停止的新型判定准则，该准则可以实现时频平面最优路径的快速搜索，提高了瞬时频率的估算精度和计算速度。通过仿真信号和实验数据进行验证，具有判定准则的改进后算法较改进前算法的效率明显提高，为无转速计的轴承状态监测和故障诊断奠定了基础。

[1] 赵晓平，张令弥，郭勤涛. 旋转机械阶比跟踪技术研究进展综述[J]. 地震工程与工程振动, 2008, 28(6): 213-219.

Zhao Xiaoping, Zhang Lingmi, Guo Qintao. Advances and trends in rotational machine order tracking methodology[J]. Journal of Earthquake Engineering and Engineering Vibration, 2008, 28(6): 213-219. (in Chinese)

[2] 陈平. 信号瞬时频率的估计方法及其应用[D].济南：山东大学, 2007.

[3] 郭瑜，秦树人，汤宝平，等. 基于瞬时频率估计的旋转机械阶比跟踪[J]. 机械工程学报，2003, 39(3): 32-36.

Guo Yu, Qin Shuren, Tang Baoping, et al. Order tracking of rotating machinery based on instantaneous frequency estimation[J]. Journal of Mechanical Engineering, 2003, 39(3): 32-36. (in Chinese)

[4] 胡爱军，朱瑜. 基于改进峰值搜索法的旋转机械瞬时频率估计[J]. 振动与冲击，2013, 32(7): 113-117.

Hu Aijun, Zhu Yu. Instantaneous frequency estimation of a rotating machinery based on an improved peak search method[J]. Journal of Vibration and Shock, 2013, 32(7): 113-117. (in Chinese)

[5] 杨志坚，丁康，梁茜. 基于频谱校正理论的阶比跟踪分析[J]. 机械工程学报，2009, 45(12): 41-45.

Yang Zhijian, Ding Kang, Liang Qian. Novel method of order tracking analysis based on spectrum correction[J]. Journal of Mechanical Engineering, 2009, 45(12): 41-45. (in Chinese)

[6] 赵晓平. 旋转机械阶比分析研究与软件实现[D]. 南京：南京航空航天大学, 2008.

[7] 赵晓平，赵秀莉，侯荣涛，等. 一种新的旋转机械升降速阶段振动信号瞬时频率的估计算法[J]. 机械工程学报, 2011, 47(7): 104-108.

Zhao Xiaoping, Zhao Xiuli, Hou Rongtao, et al. A new method for instantaneous frequency estimation of run-up or run-down vibration signal for rotating machinery[J]. Journal of Mechanical Engineering, 2011, 47(7): 104-108. (in Chinese)

[8] Leclere Q, André H, Antoni J. A multi-order probabilistic approach for Instantaneous Angular Speed tracking debriefing of the CMMNO′14 diagnosis contest[J]. Mechanical Systems and Signal Processing, 2016(81): 375-386.

[9] Combet F, Zimroz R. A new method for the estimation of the instantaneous speed relative fluctuation in a vibration signal based on the short time scale transform[J]. Mechanical Systems and Signal Processing, 2009, 23(4): 1382-1397.

[10] Urbanek J, Barszcz T, Antoni J. A two-step procedure for estimation of instantaneous rotational speed with large fluctuations[J]. Mechanical Systems and Signal Processing, 2013, 38(1): 96-102.

[11] Viterbi A. Error bounds for convolutional codes and an asymptotically optimum decoding algorithm[J]. IEEE Transactions on Information Theory, 1967,13(2):260-269.

[12] Martell A. Edge detection using heuristic search methods[J]. Comput, Graphic,Image Process, 1982,1(2): 69-182.

[13] 陈源，江修富. Viterbi算法的关键问题研究及DSP实现[J]. 装备指挥技术学院学报, 2005,16(5):77-81.

Chen Yuan, Jiang Xiufu. Study on the main problems of viterbi algor ithm and the realization of DSP[J]. Journal of the Academy of Equipment Command & Technology, 2005,16(5):77-81. (in Chinese)

[14] 胡旭娟，梁红，蒯继武. 改进WVD的调频信号瞬时频率估计算法[J]. 弹箭与制导学报, 2007, 27(5): 329-334.

Hu Xujuan, Liang Hong, Kuai Jiwu. FM Signal IF estimation algorithm based on improved WVD[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2007, 27(5): 329-334. (in Chinese)

[15] 戴功伟. 基于自适应转频跟踪滤波的旋转机械阶次析研究[D]. 重庆：重庆大学，2013.

[16] 魏玉果. 基于自适应计算阶次跟踪的旋转机械阶次分析系统[D].重庆：重庆大学, 2007.

国家自然科学基金资助项目(11572206，11472179，U1534204，11372199)；河北省自然科学基金资助项目(A2015210005，A2016210099)；河北省人才工程培养经费资助科研项目(A2016002036)

2016-09-13；

2017-01-18

TH165.3