基于LWE的高效身份基分级加密方案
2017-11-07胡明星汤永利闫玺玺
叶 青 胡明星 汤永利 刘 琨 闫玺玺
(河南理工大学计算机科学与技术学院 河南焦作 454000)(yeqing@hpu.edu.cn)
2017-06-05;
2017-07-28
国家自然科学基金项目(61300216);河南省科技厅基础与前沿技术研究计划项目(142300410147);河南省教育厅自然科学研究项目(12A520021);河南省教育厅高等学校重点科研项目(16A520013) This work was supported by the National Natural Science Foundation of China (61300216), the Foundation and Advanced Technology Research Plan of Henan Provincial Department of Science and Technology (142300410147), the Natural Science Research Project of Henan Provincial Department of Education (12A520021), and the Key Research Project of Henan Provincial Department of Education (16A520013).
汤永利(yltang@hpu.edu.cn)
基于LWE的高效身份基分级加密方案
叶 青 胡明星 汤永利 刘 琨 闫玺玺
(河南理工大学计算机科学与技术学院 河南焦作 454000)(yeqing@hpu.edu.cn)
格上可固定维数陷门派生的身份基分级加密(hierarchical identity-based encryption, HIBE)体制,因其具有在陷门派生前后格的维数保持不变的特性而受到广泛关注,但这种体制普遍存在陷门派生复杂度过高的问题.针对这一问题,分别给出随机预言模型和标准模型下的改进方案.首先利用MP12陷门函数的特性提出一种优化的q可逆矩阵提取算法,再基于该优化算法结合固定维数的陷门派生算法和MP12陷门函数完成方案的建立和陷门派生阶段,然后与对偶Regev算法相结合完成随机预言模型下HIBE方案的构造.并且利用二进制树加密系统将该方案改进为标准模型下的HIBE方案.两方案安全性均可归约至LWE问题的难解性,其中随机预言模型下的方案满足适应性安全,而标准模型下的方案满足选择性安全,并给出严格的安全性证明.对比分析表明:在相同的安全性下,随机预言模型下的方案较同类方案在陷门派生复杂度方面显著降低,而标准模型下的方案是同类最优方案的16,且格的维数、陷门尺寸和密文扩展率等参数均有所降低,计算效率明显优化.
格;基于身份的分级加密;陷门派生;容错学习;随机预言模型;标准模型
基于身份加密(identity-based encryption, IBE)是一种高级的公钥加密体制,该体制可使用用户任意的身份标识符(如邮箱地址、手机号码等)作为公钥,相应的私钥由可信第三方私钥生成中心(key generation center, KGC)利用系统主私钥生成.基于身份加密的思想首先于1984年由Shamir[1]首次提出,但直到2001年,可实际应用的IBE方案才由Boneh等人[2]提出并定义了IBE的安全模型.此后IBE的研究引起密码学者的广泛关注,很多IBE的相关方案被相继提出[3-6].
基于身份的分级加密(hierarchical identity-based encryption, HIBE)体制是IBE体制的一种推广.在HIBE体制中,多个KGC实体按照有向树的结构分布.HIBE可以更好地应用在大规模网络的应用场景中,有效解决IBE体制在大量的用户请求下无法为每一用户完成身份信息的有效验证并为之安全传送私钥的问题.HIBE体制的特点是体制中每个子KGC陷门均由它的父KGC指定,该过程称为陷门派生.应当注意的是陷门派生是单向的,这意味着每个子KGC均不能利用它的陷门来恢复父KGC或同级KGC的陷门.
近几年,基于格理论构造的新型密码体制因具有较好的渐进效率、运算简单、可并行化、抗量子攻击和存在最坏情况下的随机实例等优点,成为后量子密码时代的研究热点,并取得一系列的研究成果[7-11].2008年,Gentry等人[12]于STOC’08上利用格的短基作为陷门构造出一种格上原像采样算法,并提出对偶Regev算法;基于这2个算法和Ajtai等人[13]提出的陷门生成算法构造出格上IBE方案,并且指出在构造(H)IBE方案时应采用对偶Regev算法来完成方案的加解密阶段,比采用非对偶Regev算法更加合理,随后基于对偶Regev算法的(H)IBE方案[14-17]被相继提出.但Gentry等人提出的IBE体制的缺陷是所基于的原像采样算法和陷门生成算法太过复杂,算法的运行时间不满足实际应用;2010年,Cash等人[18]基于Gentry等人的原像采样算法构造出一种格上陷门派生算法,并基于此构造出格上首个HIBE方案,但陷门派生算法的派生陷门的维数与系统分级的深度呈2次幂增长关系,这将导致在较高的系统分级中出现格的维数、陷门尺寸等参数过大而导致陷门派生的复杂度过高的问题;2010年,Agrawal等人[19]于EUROCRYPT 2010上对Cash等人的方案进行了改进,将按照用户身份向量每1比特分配矩阵的方式改进为按系统分级中每一级分配1个矩阵的方式,从而使格的维数随着系统分级深度的增长而仅呈线性增长,但维数的增长仍然会导致格的维数、陷门尺寸等参数的膨胀而导致陷门派生复杂度过大;2010年,Agrawal等人[20]于CRYPTO 2010上提出一种固定维数的格上陷门派生技术,即格的维数在陷门派生前后保持不变,并基于此构造出一种高效的HIBE方案.格的维数是格上密码方案的重要参数与密钥长度、密文尺寸和密文膨胀率等参数密切相关,因此格上固定维数的陷门派生技术引起密码学领域的广泛关注.但该方案和陷门派生算法的构造均依赖一种q可逆矩阵的提取算法(SampleR),而该算法效率取决于原像采样算法,但Agrawal等人所采用的原像采样算法由上述的文献[12]中提出,该算法的输入是高精度的实数且是迭代化运算,这将导致SampleR算法的复杂度过高,进而影响陷门派生的效率.
2012年,Micciancio等人[21](Micciancio和Peikert于2012年发表的文章简称MP12)于EUROCRYPT 2012上提出一种新的格上陷门生成算法和与之对应的原像采样算法,相比文献[17,22]提出的陷门生成算法,该陷门生成过程简单,复杂度仅相当于2个随机矩阵的1次乘运算,且不涉及计算代价高的埃尔米特正规形式(hermite normal form, HNF)和矩阵求逆操作.相比文献[12]的原像采样算法,MP12原像采样算法较简单高效,且算法支持并行运算且输入项为小整数,对离线空间的需求较低.另外,Micciancio等人还提出了一种新的陷门派生算法,该算法相比Cash等人的算法较高效,因为该算法无须进行线性无关检测,且派生陷门的维数与系统分级的深度仅呈线性增长的关系,但维数增长导致陷门派生低效的问题仍然没有解决.
为使基于固定维数派生技术的HIBE方案更具有实际应用可行性,必须解决其陷门派生复杂度过高的问题.因此,本文提出一种高效的格上HIBE方案.主要贡献有:1)利用MP12陷门函数[21]的特性构造出一种优化的SampleR算法;2)基于优化的SampleR算法结合固定维数的陷门派生算法和高效MP12陷门生成算法完成HIBE方案的陷门生成和陷门派生阶段,然后与对偶Regev算法有机结合完成随机预言模型下的方案构造;3)利用Cash等人提出的二进制树加密系统消除随机预言机假设,从而改进为标准模型下的HIBE方案.采用与同类方案相同的安全模型进行严格的安全性证明,证明结果表明:本文2个方案的安全性均可归约至容错学习(learning with errors, LWE)问题的难解性,其中随机预言下的HIBE方案满足IND-aID-CPA安全性,标准模型下的HIBE方案满足IND-sID-CPA安全性.在效率对比分析中,为更好地体现对比结果,我们将HIBE陷门派生前的参数和计算效率与派生后的分开进行对比.对比结果表明:与相同安全性的方案相比,本文随机预言模型下的方案在陷门派生复杂度方面显著降低,而标准模型下的方案是同类最优方案的1/6,且格的维数、陷门尺寸和密文扩展率等参数均有所降低,计算效率明显优化.
1 预备知识
1.1格的相关定义
定义1. 格的定义.设b1,b2,…,bm是n上m个线性无关向量,格Λ定义为所有这些向量的整系数线性组合,即:
其中,向量组b1,b2,…,bm称为格的一组基.
定义2.q元格.设q,n,m∈,A∈n×mq,且u∈nq,定义:

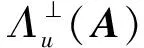
定义3. 离散高斯分布.对任意σ>0,定义以向量c为中心、σ为参数的格Λ上的离散高斯分布为
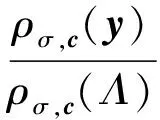
其中,y∈Λ,ρσ,c(y)=exp(-π‖y-c‖σ2).
1.2相关算法和困难问题
本文方案构造所基于的MP12陷门生成算法和与之对应的MP12原像采样算法分别由引理1和引理2给出;SampleR算法由引理3给出;固定维数的陷门派生算法由引理6给出;引理4是引理6的基本算法;对偶Regev算法的具体描述请参阅文献[12];随机预言模型下方案的安全性证明基于引理7、引理8和定义4;标准模型下方案的安全性证明基于引理8和定义4;方案的正确性证明基于引理2和引理9.
定义4[7]. 容错学习(learning with errors, LWE)问题. 设n为正整数,q为素数,对任意0<α≤1ω(),定义Ψα为中心是0、标准差是α的[0,1)上的正态分布,对应的q上的离散分布为为q上的容错分布,(q,n)-LWE问题实例由未指明的挑战预言机O构成:预言机O是带噪音的伪随机预言机Os或者是真随机的预言机O$,2种预言机的输出分别如下:
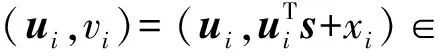
O$:输出nq×q上的真随机且均匀的采样值.
是不可忽略的,其中LWE-adv[A]表示A解决(q,n)-LWE问题的优势.
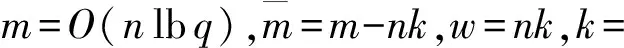
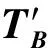
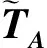
引理4[20]. SampleRwithTrap算法.与引理1参数相同.设除了至多q-n部分之外所有的A0∈n×mq,算法SampleRwithTrap输出一个m×m矩阵R,具体是从与Dm×m统计接近的分布上随机选取矩阵R的列向量.且算法SampleRwithTrap输出的A0R-1的陷门矩阵TB满足:
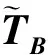
引理5[20]. 与引理1参数相同,设e为m中某向量,向量mq,则|eTy|可看作[0,q-1]中的整数,满足|eTy|≤‖e‖qαω()+‖e‖2.
引理6[20]. SampleR算法.与引理1参数相同,设T是格m的格基,利用与引理8类似的原像采样算法随机抽取m个向量ri←Sample(m,T,σR,0),其中i=1,2,…,m,将ri作为矩阵R的列向量.如果矩阵R是q可逆(矩阵R是q可逆指矩阵Rmodq仍是m×m上的可逆矩阵)的,则输出R,否则重新抽取ri.
引理7[21]. MP12陷门生成算法.与引理1参数相同,令H∈n×nq为可逆矩阵,G∈n×wq是构造公开的矩阵.选取一个均匀随机矩阵q,存在概率多项式时间(probabilistic polynomial time, PPT)算法输出矩阵‖HG-n×mq和陷门矩阵TA0=[a1‖a2‖…‖aw]∈,陷门尺寸s1(TA0)≤×ω(),其中A0在n×mq上是统计均匀的,TA0是矩阵A0的陷门.
引理8[21]. MP12原像采样算法.与引理1参数相同,设u∈nq为均匀随机向量,充分大的高斯参数σ=O(),ω()表示渐进性高于,则存在概率多项式时间算法MP12Sample(A0,M,TA0,u,σ),其中,M∈n×wq,输出向量e∈,且e的分布与统计不可区分‖e‖>σ]≤negl(n),其中).
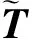
2 算法设计及方案构造
2.1符号说明
为表述方便,对文中符号进行说明,如表1所示:

Table 1 Notations Description表1 符号说明
2.2优化的SampleR算法
本节构造的优化SampleR算法的功能与Agrawal等人提出的陷门派生算法中的(见引理6)相同.由于SampleR算法输出的R矩阵是公开的,且算法的时间复杂度主要来自于算法中循环调用的原像采样算法.所以我们考虑采用较高效的MP12原像采样算法MP12Sample(见引理8).具体方法是利用MP12陷门函数中构造公开的特殊矩阵G和其公开陷门矩阵TG来进行SampleR算法中的原像采样操作.具体优化算法如下:
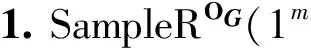
输入:整数m=O(nlbq)、用来在陪集Λ⊥(G)高斯采样的预言机OG、其高斯参数为σG;
2) Fori=1,2,…,mdo:
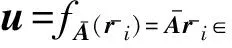
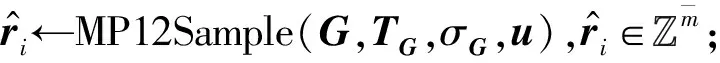
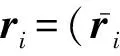
3) 将ri作为矩阵R的列向量,检测R是否是q可逆,是则输出R,否则重新进行步骤2.
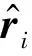
相比Agrawal等人[20]提出的SampleR算法:首先,在效率上,MP12Sample算法的输入项是小整数可支持并行化运算而不是输入项是高精度实数的正交化迭代运算,且原像采样过程中利用G矩阵和G矩阵陷门的特殊构造,时间复杂度相比通常的原像采样算法的Ω(n2lb2n)可降至O(nlbcn),其中c是常数.因此,相比Agrawal等人提出复杂度是Ω(n3lb3nn)的SampleR算法,我们的算法复杂度是O(n2lbcn).其次,在输出质量(原像采样算法的输出质量为所采样向量的范数)上,质量好坏与原像采样大小限制参数β负相关.Agrawal等人的HIBE方案采用的是文献[21]的陷门生成算法和文献[12]的原像采样算法,则βAgrawal>45nlgq,而本文βour≈2.3nlgq,相比之下本文有近19倍的提升.
我们的优化算法存在的不足是相比Agrawal等人的SampleR算法多了第2步中的②操作,该操作采用高效正向计算的方式输出,复杂度仅等同于执行1次Hash算法.
2.3随机预言模型下的HIBE方案
方案具体构造如下,其基本参数包括:均匀随机矩阵A0∈n×mq和其陷门R0∈,其中n是安全参数,d是系统支持的最大分级深度,用户身份id=(id1‖id2‖…‖id)∈({0,1}*),其中∈[d],i∈[1,].令其中.一个构造公开的矩阵G=In⊗gT∈n×nkq,其中In是n×n单位矩阵,gT=(1,2,22,…,2k-1)∈kq;随机预言机H:({0,1}*)≤d→m×mq:id|→H(id)~Dm×m.
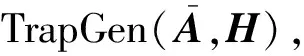
HIBE-Derive(MPK,SKi d|,id):输入主公钥MPK;输入SKi d|表示系统分级深度为时用户公钥矩阵Ai d|所对应的陷门矩阵,其中n×mq,父用户身份id=(id1‖id2‖…‖id),可逆矩阵Ri d|=H(id|1)H(id|2)…H(id)∈m×m;输入子用户身份id=(id1‖id2‖…‖id‖id‖…,‖其中d.计算R=H(id)H(id)…H(id|k)∈m×m并令Ai d=Ai dR-1.调用引理2的陷门派生算法输出陷门矩阵SKi d=S′.另外,将参数Ai d0设为A0,SKi d|0设为TA0,HIBE-Derive算法相当于IBE方案中的用户密钥提取算法IBE-Extract.

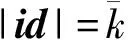
2.4标准模型下的HIBE方案

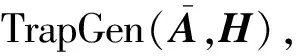
HIBE-Derive(MPK,SKi d|,id):输入主公钥MPK;输入SKi d|表示系统分级深度为时用户公钥矩阵Ai d|所对应的陷门矩阵,其中Ai d=A0(R1,id1)-1(R2,id2)-1…(R)-1∈n×mq,父用户身份id={0,1};输入子用户身份id=(id1‖id2‖…‖id‖id‖…,‖其中d.令m×m,Ai d=Ai dR∈n×mq.调用2.3节的陷门派生算法输出陷门矩阵SKi d=S′.
3 安全性证明
通常,一个HIBE方案的安全性需满足选择身份攻击和选择明文攻击下的密文不可区分性(IND-ID-CPA),根据安全强度不同,分为适应性选择身份选择明文攻击(IND-aID-CPA)和选择性选择身份选择明文攻击(IND-sID-CPA).本文方案在随机预言模型下满足IND-aID-CPA安全,在标准模型下满足IND-sID-CPA安全.
本方案采用Agrawal等人[19]在EEUROCRYPT 2010上提出的格上HIBE方案的INDr-s/aID-CPA安全模型进行安全性证明,该安全模型不仅可证明IND-s/aID-CPA安全,还可以保护接收方的匿名性,且主公钥的私密性可被其创建的密文保护.基于该安全模型进行安全证明的还有2010年Agrawal等人[20]于CRYPTO 2010和2016年Wang等人[24]于FITEE提出的HIBE方案.
正确性. 本文HIBE方案的解密正确性由定理1刻画.
定理1. 本文HIBE方案的解密是正确的,对任意的id∈ID,(MPK,MSK)←HIBE-Setup(1n,d),ski d←HIBE-Extract(MPK,R,(id1‖id2‖…‖id)‖id)和消息b∈{0,1},其中ID为身份空间,有
Pr[Decrypt(MPK,ski d,Encrypt(MPK,id,b))=b]=1-negl(n)成立.
证明. HIBE方案解密算法的输出为
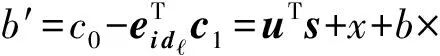

Table 2 Parameters Setting of HIBE Scheme Under Random Oracle Model
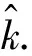
Table3ParametersSettingofHIBESchemeUnderStandardModel

表3 标准模型下HIBE方案的参数设置
表2和表3所示的参数设定下,本文2.3节和2.4节的HIBE方案中的error-term均小于q5,则方案正确性得以保证.
证毕.
安全性. 本文随机预言模型下的HIBE方案的安全性由定理2刻画.
定理2. 设A为攻击2.3节随机预言模型下HIBE方案的PPT攻击者,H为随机预言机H:({0,1}*)≤d→m×mq.令QH为敌手A对可对H询问的最大次数,d为系统可支持的最大分级深度,则存在一个PPT算法B满足:如果A是一个具有优势ε的适应性攻击者(INDr-aID-CPA),那么).
证明. 已知LWE问题是区分定义4中预言机O的输出是来自伪随机预言机Os还是真随机预言机O$.基于A的能力,构造一个优势是ε的DLWE算法B.
B对预言机O进行询问并获取一组实例(ui,vi)∈nq×q,其中i=1,2,…,m,要求B通过模拟游戏并基于A的能力区分出实例来自预言机Os或O$.模拟过程如下:
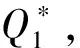
u0∈nq;选取一个随机整数φ∈[d]并令因A在n×mq上是均匀的,且是模q可逆的,则A0在n×mq上是均匀的.输出主公钥MPK=(A0,u0).
模拟随机预言机. 对于适应性的攻击者A,A能够在任意时间适应性地选择任意用户身份id=id1,id2,…,idi提交给随机预言机H进行询问.假设A的询问是唯一的,否则B对相同的输入返回相同的内容且不增加询问计数器Q的值.令i=|id|为用户身份的深度,对于A的询问B的回应分2种情况:
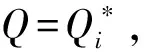
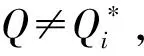
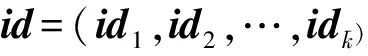
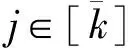

3) 运行2.3节HIBE方案中的Derive(MPK,TB,id)算法,利用父身份id|j的陷门矩阵TB派生出子身份id的陷门矩阵.如果j=k,直接运行引理5中的RandBasis(TB,σk)算法.输出并发送id的陷门矩阵至攻击者A.
挑战阶段.攻击者A向模拟者B宣布待攻击的用户身份id*并输出一个消息比特b*∈{0,1}.要求id*不能是攻击者A已经询问或即将询问的用户身份的父身份.令=|id*|,如果存在i∈[]满足模拟终止.已知如果φ≠,模拟终止.
假设φ=且对任意的i∈[]有定义将从预言机O获取到的一组实例中的v1,v2,…,vm∈q设为并令mq;利用v0盲化消息位得q/2∈q;发送挑战密文至攻击者A.若O是伪随机LWE预言机,则q/其中s←nq为均匀随机选取的向量,q和mq分别为噪音值和噪音向量,则CT*是利用挑战身份id*对消息位b*的有效加密密文;若O是真随机预言机,则(v0,v*)在q×mq上是均匀的,那么挑战密文在q×mq上也是均匀的.
模拟私钥派生.该阶段与挑战前阶段的前的模拟私钥派生阶段相同,攻击者A可以继续选择用户身份进行私钥询问,模拟者B以同样的方式进行回应.最后,攻击者A猜测挑战密文CT*是否是利用挑战身份id*对消息位b*的有效加密密文,模拟者B输出A的猜测并结束模拟.
由以上可知,主公钥中参数的分布与实际系统中陷门派生算法所需的参数的分布是相同的.且由引理3可知,对随机预言机H询问的回应与实际系统是相同的.如果模拟者B不终止模拟,则挑战密文CT*的分布在(q×mq)上是独立随机的或与实际系统相同.因此,如果模拟者B不终止模拟,则B在区分DLWE问题上的优势与攻击者A成功攻击方案的优势相同.对于PPT攻击者A来说,A在随机预言机上发现碰撞的概率是可忽略的,则模拟者B可进行而不终止的概率是Pr[d-negl(n).因此,如果攻击者A的优势是ε,则模拟者B解决LWE问题实例的优势至少是[ε).
证毕.
安全性.本文标准模型下的HIBE方案的安全性由定理3刻画.

证明. 假设攻击者A在区分定义4中预言机O的输出的具有不可忽略的优势,我们基于A的能力构造一个LWE算法B.
B对预言机O进行询问并获取一组实例(ui,vi)∈nq×q,其中i=1,2,…,m,要求B通过模拟游戏并基于A的能力区分出实例来自预言机Os或O$.模拟过程如下:

系统建立:模拟者B首先利用实例(ui,vi)∈nq×q生成随机矩阵A∈n×mq,矩阵A的第i列是向量ui,i=1,2,…,m,将向量u0作为公共随机向量u0∈nq;然后利用2.2节优化的SampleR算法抽取个随机矩阵m×m,令考虑如下d个矩阵
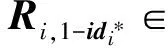
模拟私钥派生:模拟者B利用系统建立阶段调用引理4中的SampleRwithTrap生成的陷门矩阵TAi来回应攻击者A的私钥询问.要求攻击者A询问的用户身份不能是目标身份id*的父身份.模拟者调用2.4节HIBE方案中的Derive(MPK,TAi,id)算法,利用攻击者所查询身份的父身份的陷门矩阵TAi派生出所查询身份的陷门矩阵.如果i=d,直接运行引理1中的RandBasis(TAi,σd)算法.输出并发送id的陷门矩阵至攻击者A.
挑战阶段.攻击者A向模拟者B发送一个消息比特b*∈{0,1},B将从预言机O获取到的一组实例中的v1,…,vm∈q设为并令v*∈mq;利用v0盲化消息位得q/2∈q;选取一个随机位r←{0,1},如果r=0,发送挑战密文至攻击者A,如果r=1,选取一个随机的CT*=(c0,c1)∈q×mq发送给攻击者.

猜测阶段.在攻击者A完成又一轮的私钥询问后,攻击者A猜测收到的挑战密文CT*是来自伪随机预言机Os还是是真随机的预言机O$.模拟者B输出A的猜测结果作为对LWE问题的求解.

证毕.
4 效率分析
本节对随机预言模型下和标准模型下的HIBE方案分别进行效率分析.为更好地体现本文HIBE方案的优越性,我们将HIBE陷门派生前的参数和计算效率与派生后的分开进行对比.为简单直观,我们将派生前和派生后的分级深度设为=1和=2.
4.1随机预言模型下的HIBE方案效率分析
我们选择2个随机预言模型下的HIBE方案作为参照对象:Cash等人[18]于EUROCRYPT 2010提出的随机预言模型下适应性安全的首个格上HIBE方案(简称CHKP方案);Agrawal等人[19]于CRYPTO 2010上提出的一种具有较短密文尺寸且可固定维数派生的随机预言模型下适应性安全的HIBE方案(简称ABBa方案).设安全参数n=284,q=2的24次方.对比结果如表4和表5所示,其中RO-adaptive表示该方案满足随机预言模型下INDr-aID-CPA安全性.
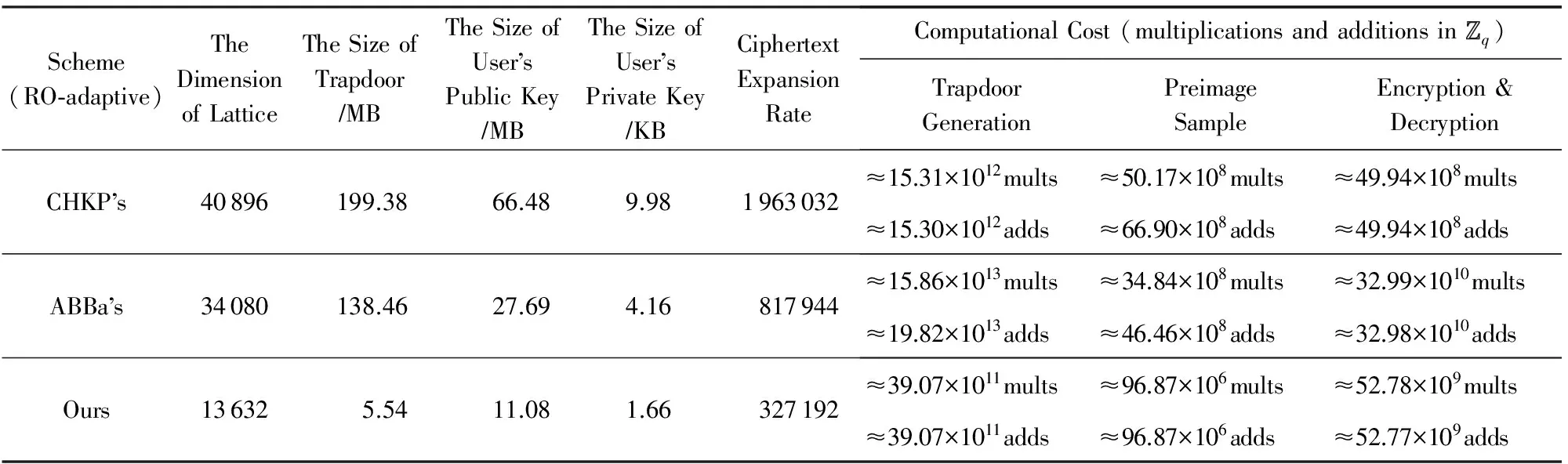
Table 4 Efficiency Comparison of HIBE Schemes Before Trapdoor Delegation Under Random Oracle Model表4 随机预言模型下的HIBE方案陷门派生前效率对比
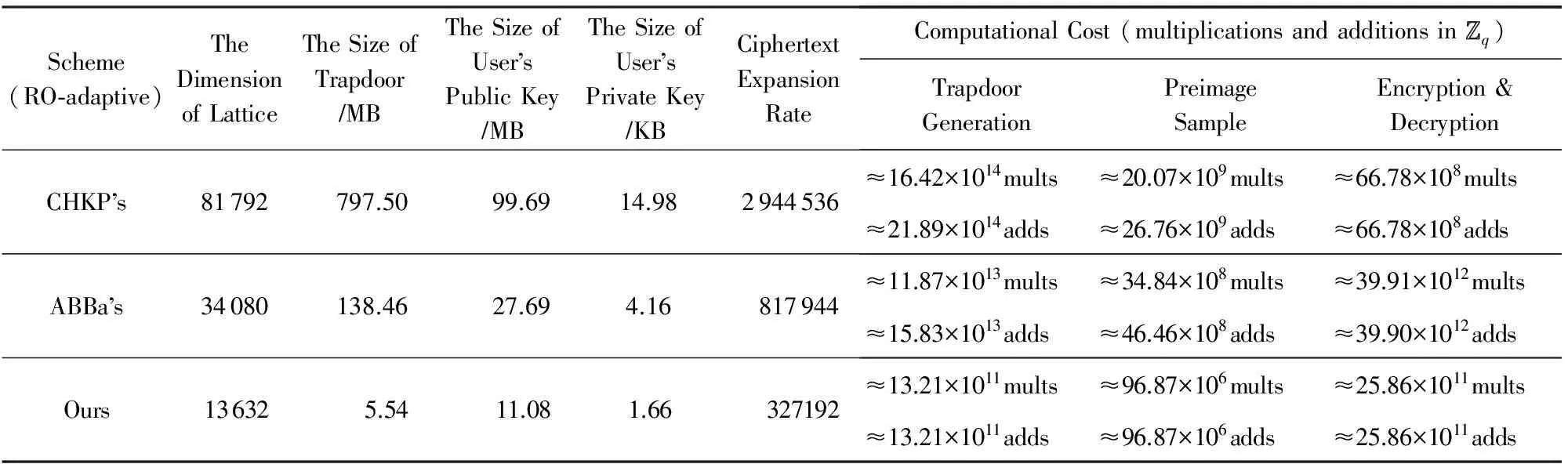
Table 5 Efficiency Comparison of HIBE Schemes After Trapdoor Delegation Under Random Oracle Model表5 随机预言模型下的HIBE方案派生后效率对比
由表4和表5对比可以看出,相比CHKP方案,ABBa方案和本文方案的主要优势在于陷门派生前后格的维数保持不变,因此效率参数如陷门尺寸、用户公私钥尺寸、明文-密文扩展率以及计算效率上的原像采样算法的复杂度均保持不变.但是,基于固定维数陷门派生技术的HIBE方案存在的主要缺点是加密复杂度较大,原因是:当加密者向分级深度为的用户发送消息时,需要计算个m×m矩阵的连续乘积.但优点是该运算对于每个用户身份只需进行1次,且与发送的消息是无关的.
相比同是固定维数陷门派生的ABBa方案,本文方案的优势在于具有较低的格的维数.原因在于所采用的MP12陷门生成算法(见引理7)输出的矩阵A∈n×mq的维数仅为2nlbq时,矩阵A的分布与均匀分布的统计距离即可满足是安全参数n的可忽略函数.且陷门生成算法所输出陷门不再是格Λ⊥(A)的格基,而是从特定概率分布随机抽取的短向量组成的陷门矩阵,因此陷门矩阵的尺寸相比表中其他方案较小.此外,低维数和小的陷门尺寸也是用户公钥和私钥尺寸较短的主要原因.
在陷门生成复杂度上,相比ABBa方案,本文方案具有明显的优势.原因在于本文方案在陷门生成过程中不存在计算代价高的HNF和矩阵求逆操作,陷门生成的复杂度仅相当于2个随机矩阵的1次乘运算;在原像采样复杂度上,本文方案是ABBa方案的513倍,原因在于原像采样算法使用小整数作为输入项且支持并行化运算,而不是使用输入项是高精度实数的正交化迭代运算;在陷门派生上,本文方案比其他方案高效的原因在于,陷门派生算法复杂度主要取决于所调用的SampleR算法(见引理6)和RandBasis算法(见引理1),而它们效率的根本都取决于所调用的原像采样算法.在2.2节我们分析所调用的原像采样算法的时间复杂度相比通常原像采样算法的Ω(n2lb2n)可降至O(nlbcn),且基于固定维数派生陷门算法的HIBE方案的陷门派生复杂度不会随系统分级深度的增长而变高.
4.2标准模型下的HIBE方案效率分析
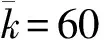

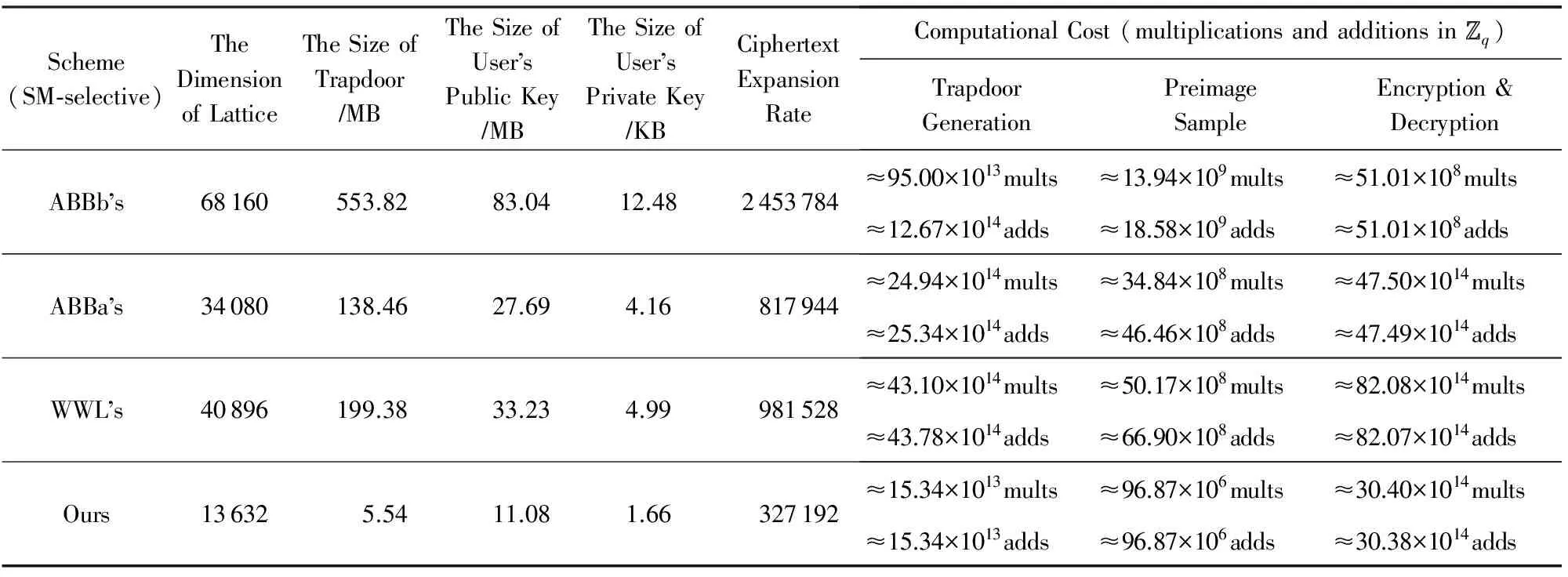
Table 7 Efficiency Comparison of HIBE Schemes After Trapdoor Delegation Under Standard Model表7 标准模型下的HIBE方案派生后效率对比
在陷门派生上,对于固定维数派生的HIBE方案,由于ABBa和WWL方案均基于ABBa中提出的时间复杂度是Ω(n3lb3n)的SampleR算法,本文方案采用2.2节优化后的SampleR算法可将算法时间复杂度降至O(n2lbcn),c为常数;对于非固定维数派生的HIBE方案,其时间复杂度与格的维数紧密相关.由表7可以看出,在系统分级深度仅为2时,本文方案相比ABBb方案已有6倍的提升,且基于固定维数派生的HIBE方案因为格的维数在陷门派生前后不变,因此陷门派生的时间复杂度不受系统分级深度的影响.
综上所述,相比同类方案,本文方案在随机预言模型和标准模型下的陷门派生复杂度有效降低,且方案的效率参数和计算效率整体有所提高.因此,本文方案总体上是较高效的.
5 总 结
为解决格上基于固定维数陷门派生技术的HIBE方案中陷门派生复杂度过高的问题,本文提出一种高效的q可逆矩阵提取算法,并基于该算法结合固定维数的陷门派生算法和MP12陷门函数分别在随机预言模型和标准模型下给出2种改进方案.方案安全性均归约至LWE问题的难解性,其中基于随机预言模型的HIBE方案的安全性满足IND-aID-CPA安全,基于标准模型的HIBE方案安全性满足IND-sID-CPA安全.对比分析表明,格上基于固定维数派生技术HIBE方案中陷门派生复杂度过高的问题得到有效解决,且在其他效率参数和计算效率上整体提升.
本文方案的不足在于标准模型下方案安全性仅满足IND-sID-CPA安全,如何构造标准模型下IND-aID-CPA安全的格上HIBE方案是值得进一步研究的问题.
[1] Shamir A. Identity-based crypto systems and signature schemes[C] //Proc of CRYPTO 1984. Berlin: Springer, 1984: 47-53
[2] Boneh D, Franklin M. Identity-based encryption from the weil pairing[C] //Proc of CRYPTO 2001. Berlin: Springer, 2001: 213-229
[3] Waters B. Efficient identity-based encryption without random oracles[C] //Proc of EUROCRYPT 2005. Berlin: Springer, 2005: 114-127
[4] Lai Junzuo, Deng R H, Liu Shengli, et al. Identity-based encryption secure against selective opening chosen-ciphertext attack[C] //Proc of EUROCRYPT 2012. Berlin: Springer, 2012: 77-92
[5] Yamada S. Adaptively secure identity-based encryption from lattices with asymptotically shorter public parameters[C] //Proc of EUROCRYPT 2016. Berlin: Springer, 2016: 32-62
[6] Wang Fenghe, Liu Zhenhua, Wang Chunxiao. Full secure identity-based encryption scheme with short public key size over lattices in the standard model[J]. International Journal of Computer Mathematics, 2016, 93(6): 854-863
[7] Regev O. On lattices, learning with errors, random linear codes, and cryptography[J]. Journal of the ACM, 2009, 56(6): 84-93
[8] Nguyen P, Zhang Jiang, Zhang Zhenfeng. Simpler efficient group signatures from lattices[C] //Proc of Public-Key Cryptography. Berlin: Springer, 2015: 401-426
[9] Libert B, Ling San, Nguyen K, et al. Zero-knowledge arguments for lattice-based accumulators: Logarithmic-size ring signatures and group signatures without trapdoors[C] //Proc of EUROCRYPT 2016. Berlin: Springer, 2016: 1-31
[10] Brakerski Z, Perlman R. Lattice-based fully dynamic multi-key FHE with short ciphertexts[C] //Proc of CRYPTO 2016. Berlin: Springer, 2016: 190-213
[11] Zhang Yanhua, Hu Yupu. A new verifiable encrypted signature from lattices[J]. Journal of Computer Research and Development, 2017, 54(2): 305-312 (in Chinese)
(张彦华, 胡予濮. 新的基于格的可验证加密签名方案[J]. 计算机研究与发展, 2017, 54 (2): 305-312
[12] Gentry C, Peikert C, Vaikuntanathan V. Trapdoors for hard lattices and new cryptographic constructions[C] //Proc of the 40th ACM Symp on Theory of Computing. New York: ACM, 2008: 197-206
[13] Ajtai M. Generating hard instances of the short basis problem[C] //Proc of Int Colloquium on Automata, Languages and Programming. Berlin: Springer, 1999: 1-9
[14] Agrawal S, Boyen X, Vaikuntanathan V, et al. Functional encryption for threshold functions (or fuzzy IBE) from lattices[C] //Proc of Public Key Cryptography. Berlin: Springer, 2012: 280-297
[15] Ducas L, Lyubashevsky V, Prest T. Efficient identity-based encryption over NTRU lattices[C] //Proc of ASIACRYPT 2014. Berlin: Springer, 2014: 22-41
[16] Katsumata S, Yamada S. Partitioning via non-linear polynomial functions: More compact IBEs from ideal lattices and bilinear maps[C] //Proc of ASIACRYPT 2016, Berlin: Springer, 2016: 682-712
[17] Zhang Jiang, Chen Yu, Zhang Zhenfeng. Programmable hash functions from lattices: Short signatures and IBEs with small key sizes[C] //Proc of CRYPTO 2016. Berlin: Springer, 2016: 302-332
[18] Cash D, Hofheinz D, Kiltz E, et al. Bonsai trees, or how to delegate a lattice basis[C] //Proc of EUROCRYPT 2010. Berlin: Springer, 2010: 523-552
[19] Agrawal S, Boneh D, Boyen X. Efficient lattice (H) IBE in the standard model[C] //Proc of EUROCRYPT 2010. Berlin: Springer, 2010: 553-572
[20] Agrawal S, Boneh D, Boyen X. Lattice basis delegation in fixed dimension and shorter-ciphertext hierarchical IBE[C] //Proc of CRYPTO 2010. Berlin: Springer, 2010: 98-115
[21] Micciancio D, Peikert C. Trapdoors for lattices: Simpler, tighter, faster, smaller[C] //Proc of EUROCRYPT 2012. Berlin: Springer, 2012: 700-718
[22] Alwen J, Peikert C. Generating shorter bases for hard random lattices[C] //Proc of the 26th Int Symp on Theoretical Aspects of Computer Science. Berlin: Springer, 2009: 535-553
[23] Micciancio D, Goldwasser S. Complexity of Lattice Problems: A Cryptographic Perspective [G] //The International Series in Engineering and Computer Science: 671. Berlin: Springer, 2002
[24] Wang Fenghe, Wang Chunxiao, Liu Zhenhua. Efficient hierarchical identity based encryption scheme in the standard model over lattices[J]. Frontiers of Information Technology & Electronic Engineering, 2016, 17(8): 781-791
EfficientHierarchicalIdentity-BasedEncryptionSchemefromLearningwithErrors
Ye Qing, Hu Mingxing, Tang Yongli, Liu Kun, and Yan Xixi
(SchoolofComputerScienceandTechnology,HenanPolytechnicUniversity,Jiaozuo,Henan454000)
Hierarchical identity-based encryption (HIBE) in fixed dimension has drawn wide attention because its lattice dimension keeps unchanged upon delegation, but there is a common defect of high complexity in trapdoor delegation stage of these schemes. Aiming at this problem, we propose two improved HIBE schemes under random oracle model and standard model respectively. We first use the MP12 trapdoor function to construct an optimizedq-invertible matrix sample algorithm. Based on this optimized algorithm, combined with trapdoor delegation algorithm in fixed dimension and MP12 trapdoor function, we design system setup and trapdoor delegation stages. And we complete the HIBE scheme under random oracle model in conjunction with Dual-Regev algorithm. And then, we remove the random oracle by employing binary tree encryption system. The security of both proposed schemes strictly reduce to the hardness of learning with errors (LWE) problem, in which the scheme under random oracle model satisfies the adaptive security while the scheme under standard model satisfies selective security. Comparative analysis shows that, under the same security level, the overhead of trapdoor delegation in our scheme under random oracle model is reduced significantly compared with the relevant schemes, while the overhead of our scheme under standard model is reduced nearly 6 times compared with the relevant optimal schemes. Furthermore, the parameters such as lattice dimension, trapdoor size and ciphertext expansion rate etc., all decrease in some degree, and the computational cost is reduced obviously.
lattice; hierarchical identity-based encryption (HIBE); trapdoor delegation; learning with errors (LWE); random oracle model; standard model
TP309

YeQing, born in 1981. Associate professor at Henan Polytechnic University. Received her PhD degree from Beijing University of Posts and Telecommunications. Her main research interests include lattice cryptography and algebra.

HuMingxing, born in 1994. Master candidate in School of Computer Science and Technology, Henan Polytechnic University. His main research interests include information security and lattice cryptography.

TangYongli, born in 1972. Professor at Henan Polytechnic University. Senior member of CCF. Received her PhD degree from Beijing University of Posts and Telecommunications. His main research interests include information security and cryptography.

LiuKun, born in 1978. Associate professor at Henan Polytechnic University. Received her MSc degree from Chongqing University of Posts and Telecommunications. Her main research interests include cryptography and number theory.

YanXixi, born in 1985. Associate professor at Henan Polytechnic University. Received her PhD degree from Beijing University of Posts and Telecommunications. Her main research interests include lattice cryptography and algebra.
