基于ANSYS Workbench的弧面分度凸轮轴的谐响应分析

龚青山，刘刚，吴岳敏，曾国华

(1.湖北汽车工业学院机械工程学院，湖北十堰 442002；2.竹山县职业技术集团学校，湖北十堰 442200)

基于ANSYS Workbench的弧面分度凸轮轴的谐响应分析

龚青山1，刘刚2，吴岳敏1，曾国华1

(1.湖北汽车工业学院机械工程学院，湖北十堰 442002；2.竹山县职业技术集团学校，湖北十堰 442200)

应用Pro/E建立弧面凸轮轴三维模型，将三维模型导入到ANSYS Workbench中完成网格划分，然后对弧面分度凸轮轴进行谐响应分析，分析激振力对凸轮分度精度的影响，为高速弧面分度凸轮轴的应用提供理论指导。

弧面分度凸轮轴；谐响应分析； ANSYS Workbench

0 引言

机械动力学是研究机械在运转过程中的受力情况以及在这些力作用下的运动状态的一门学科。传统的弧面分度凸轮机构的动力学分析采用集中参数模型对真实机构进行简化，包括连续系统的离散化、非线性系统的线性化以及对一些次要因素的适当忽略，在这一系列繁杂的简化过程中，将很难获得精确的解析解，以至于所得结果偏差较大，更精细地描述凸轮结果的动力学行为可采用有限元法。

有限元法是把真实的连续系统离散化为有限多个单元体，单元体彼此间只在数目有限的节点处连接，组成一个有有限多个自由度的单元集合体，以代替原来的连续体，并在节点上引进等效力，使问题简化为适合于数值解法的结构型问题。

谐响应分析是用于确定线性结构在承受随时间按正弦规律变化的载荷的稳态响应的一种技术。在弧面分度凸轮机构的运动过程中，弧面凸轮的工作轮廓面与分度盘滚子之间接触时产生的相互作用力非常复杂。它不但和系统的结构尺寸相关，同时还和外部激振力的大小和激振频率有联系。文中的分析思路是：查阅凸轮设计手册得到凸轮在转盘节点处的最大受力，并将其简化为一个简谐力，然后研究这个简谐力的大小和频率对凸轮轴的响应位移和响应应力的影响。由于凸轮轴向力是影响分度盘分度精度的关键，这里只做了轴向的谐响应分析。

1 凸轮机构有限元模型的建立

1.1 结构动力学分析的有限元法理论

由于计算技术以及结构振动理论所取得的成就，机构动力学模型的建立逐步形成了以离散方法和模态综合法为基础的机构动力学模型理论。在离散单元中根据对质量处理方法的不同，可分为集中质量、分布质量两种模型。另外建立在弹性力学基础上的有限元模型也得到越来越广泛的应用。

1.2 离散化与自由度

实际构件都是连续体，它的运动可以用沿构件分布的无限个坐标来描述，但是计算量太大，所以还是需要用有限多个参数来代替实际系统。较复杂的模型可以精确地描述系统，但是它要求更加复杂的数学求解和模态分析。动力等效系统包括质量和力的等效。振型耦合即不同振型之间的耦合可能产生较低的共振频率。

2 弧面分度凸轮轴谐响应分析

2.1 尺寸及材料性能

作者运用Pro/E对弧面分度凸轮轴进行三维建模，然后导入到ANSYS Workbench中。导入后模型如图1所示。

图1 弧面凸轮轴

其材料的物理性能如表1所示。

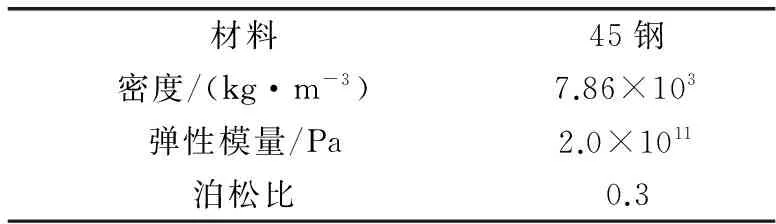
表1 弧面分度凸轮轴的物理参数

2.2 单元选择

单元的选择取决于实体的几何特征及行为特征。根据构成这些模型的几何特征、行为特征来选择单元形状。选择体单元中的四面体单元Solid187，因为四面体单元适用于不规则模型的分网，同时此单元是分析弹性结构空间问题中应用较广的一种元素。由于四面体单元Solid187是二次三维10节点单元，在每个节点有3个自由度：X、Y、Z方向,该元素具有空间的任何方向,具有二次位移行为，非常适合于不规则网格模型。网格划分如图2所示。

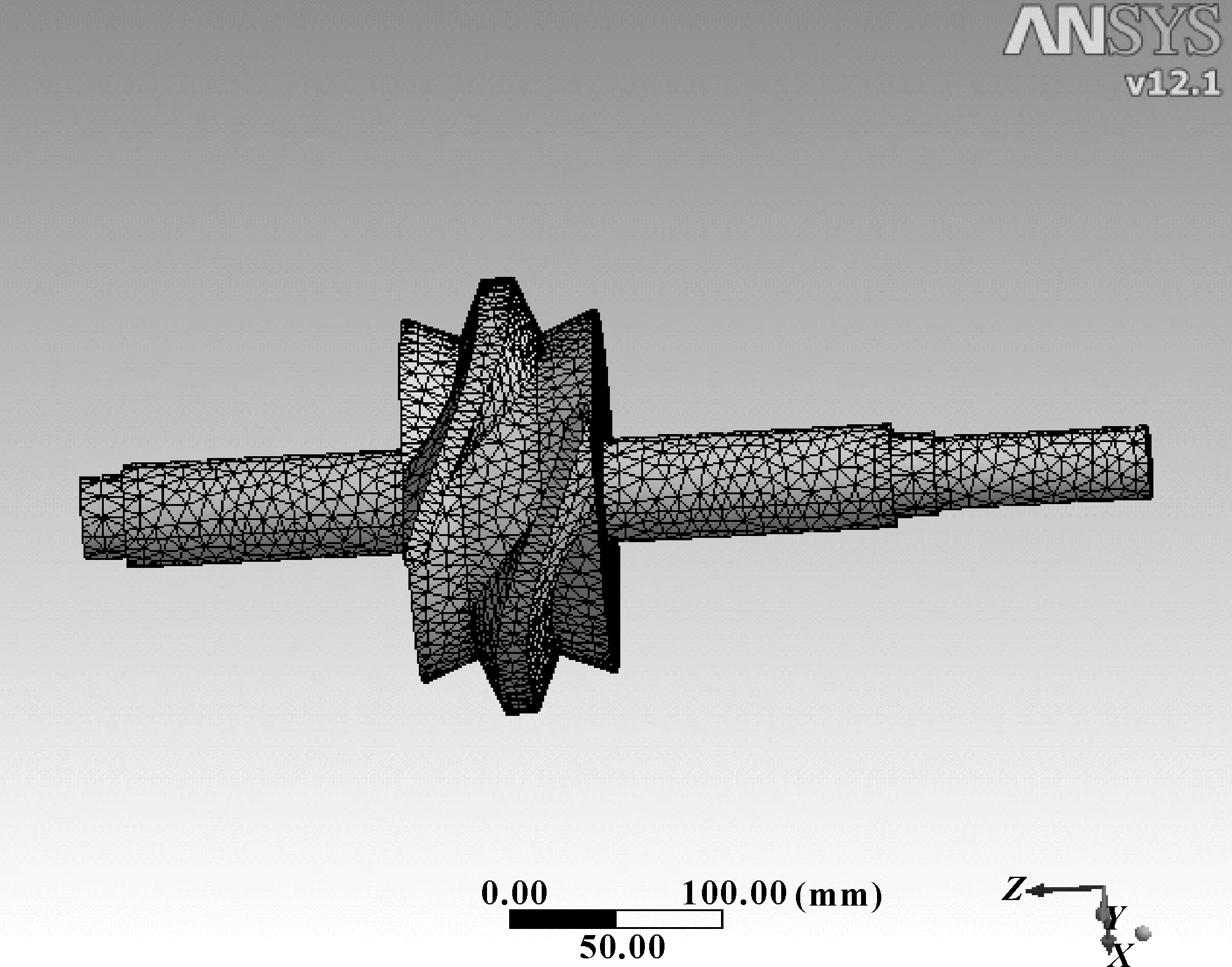
图2 网格划分图

2.3 加载及求解

根据实际情况准确建立物理模型，将弧面凸轮轴简化为一端只允许绕轴中心线旋转其余的为约束状态，另一端允许绕轴中心线旋转和移动的力学模型,力学模型如图3所示。通过计算对比发现，Fr的值相比于Me和Fa很小，在此忽略不计。计算如下:

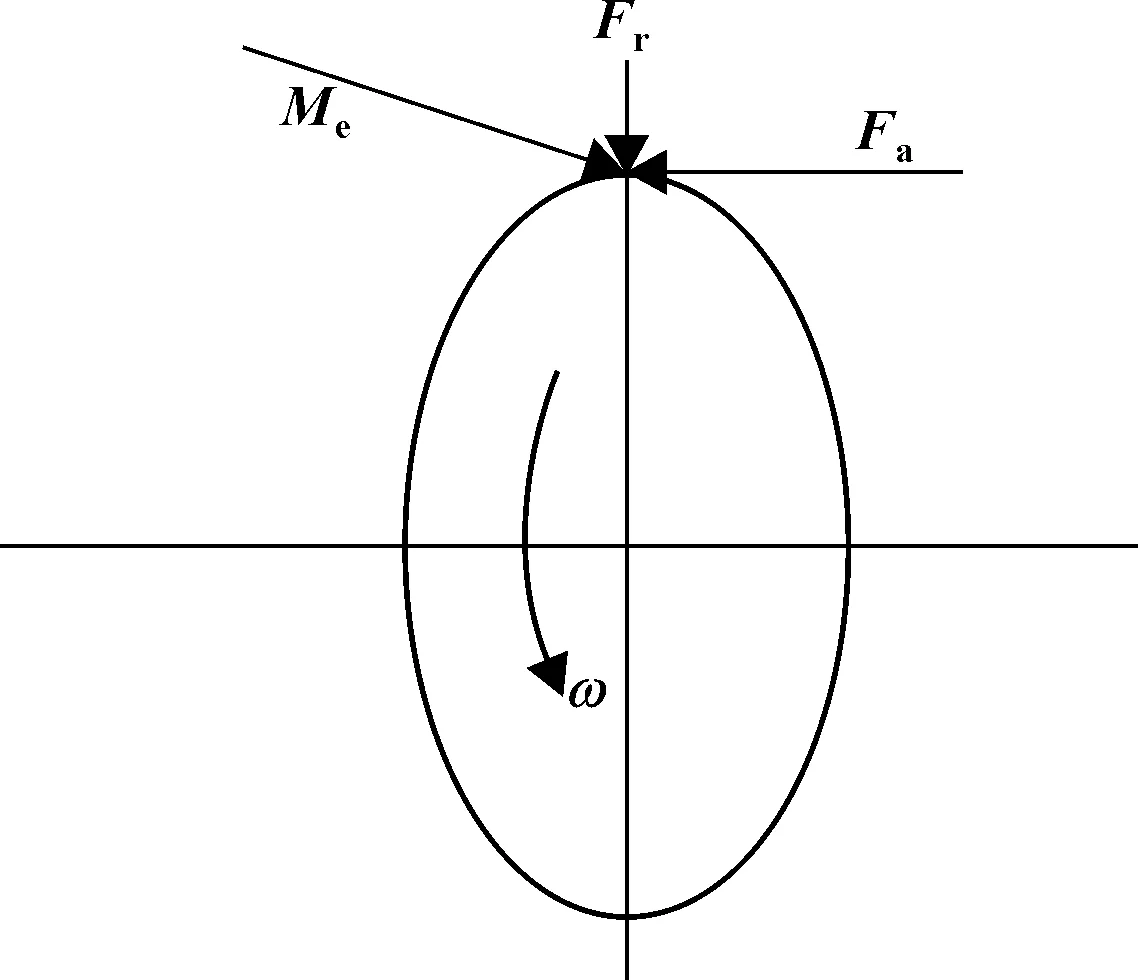
图 3 力学模型

2.3.1 凸轮参数确定

根据已加工出的弧面分度凸轮的材料和相关尺寸，计算出以下相关参数：

凸轮质量m=20.32 kg；

工作台最大转动惯量J1=150.5 N·m；

转盘与工作台最大负荷力矩与最大摩擦力矩之和：

(Mr2+Mf2)max=0.15(Mi2)max=0.15×150.5 N·m=22.57 N·m

转盘与工作台的最大惯性矩：

转盘与工作台最大阻力矩：

(Me2)max=(Mi2)max+(Mr2+Mf2)max=(150.5+22.57)N·m=173.07 N·m

凸轮上最大驱动力矩：

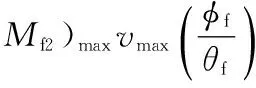
凸轮工作廓面上节点处最大轴向力:

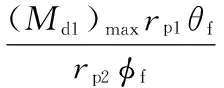
2.3.2 激振力

一个完整的激振力由幅值、相位角和激振频率组成，即：

P(t)=P1cos(ωt+φ)

其中：P1、ω和φ分别为幅值、激振角频率和相位角。

将上式按傅里叶级数展开得：

P(t)=P0+P1cos(ωt+φ1)+P2(ωt+φ2)+……

忽略高阶项，忽略常量部分，取φ1=0，则有:

P(t)=P1cos(ωt)

弧面凸轮轴的一端约束状态如图4所示， 弧面凸轮轴的另一端约束状态如图5所示。对网格划分和加载约束后的凸轮轴实体模型进行谐响应分析。

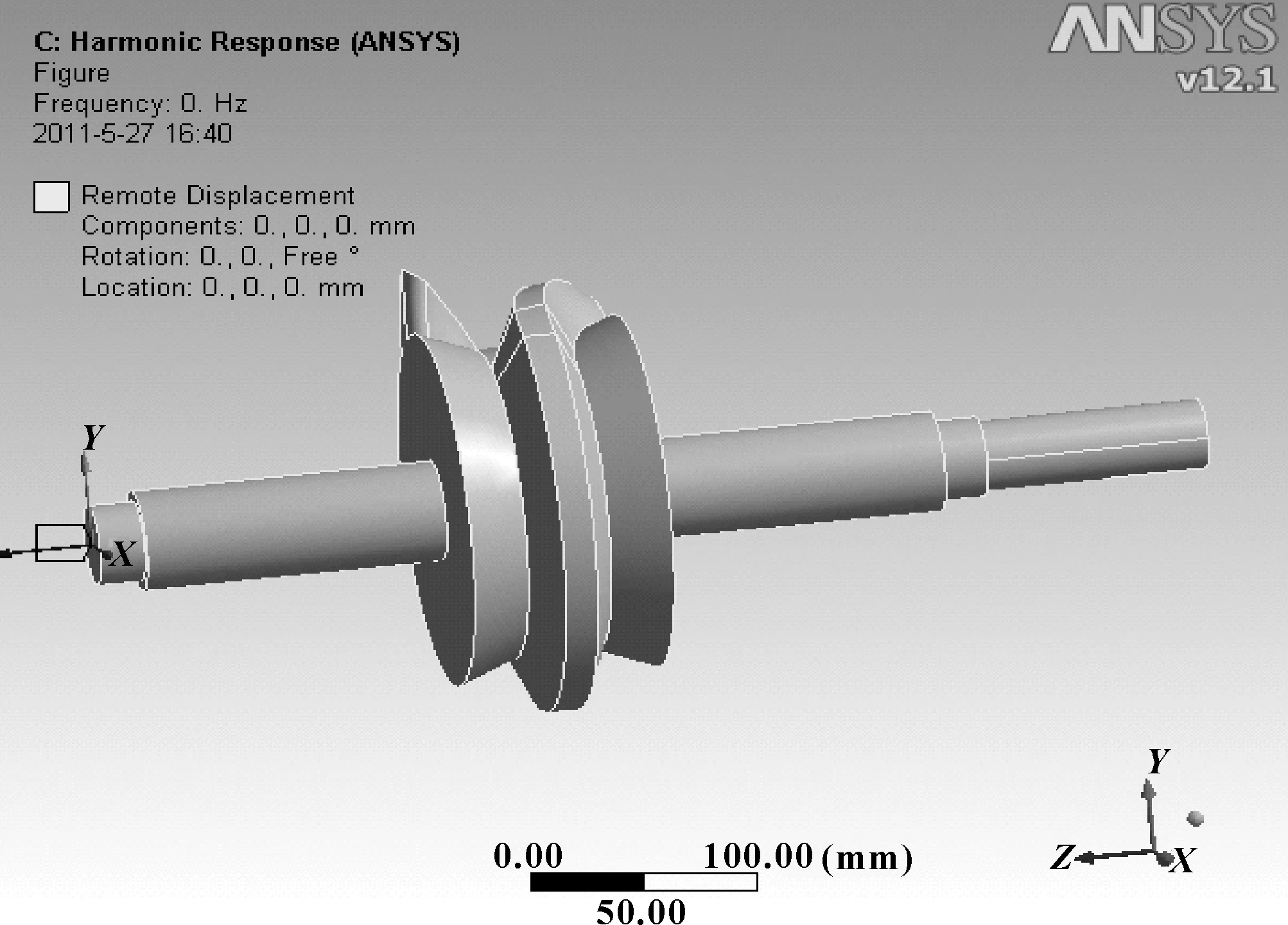
图4 弧面凸轮轴的一端约束状态

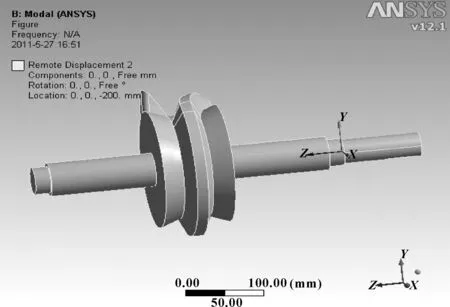
图5 弧面凸轮轴的另一端约束状态

2.4 凸轮的轴向响应

凸轮轴向最大受力取P1=(Fa1)max=2 234 N，凸轮转速n=300 r/min，激振频率f=n/60=5 Hz,激振角频率ω=2πn/60=10π(rad/s)。

在加速度达到最大值处施加激振力(前面已经表述该处位置)，由于凸轮和分度盘是线接触，所以激振力加载在此处的分度盘与滚子的接触线上。

弧面分度凸轮轴位移云图见图6，弧面分度凸轮轴向响应位移见图7，凸轮轴轴向力的响应应力图见图8，表2是最大位移和最大应力值。

图6 弧面分度凸轮轴位移云图

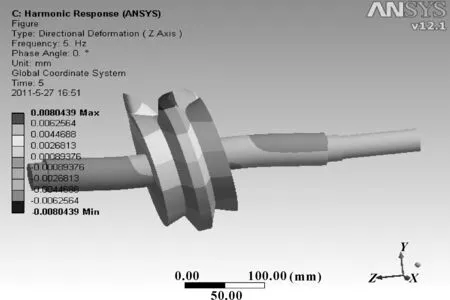
图7 弧面分度凸轮轴向响应位移图

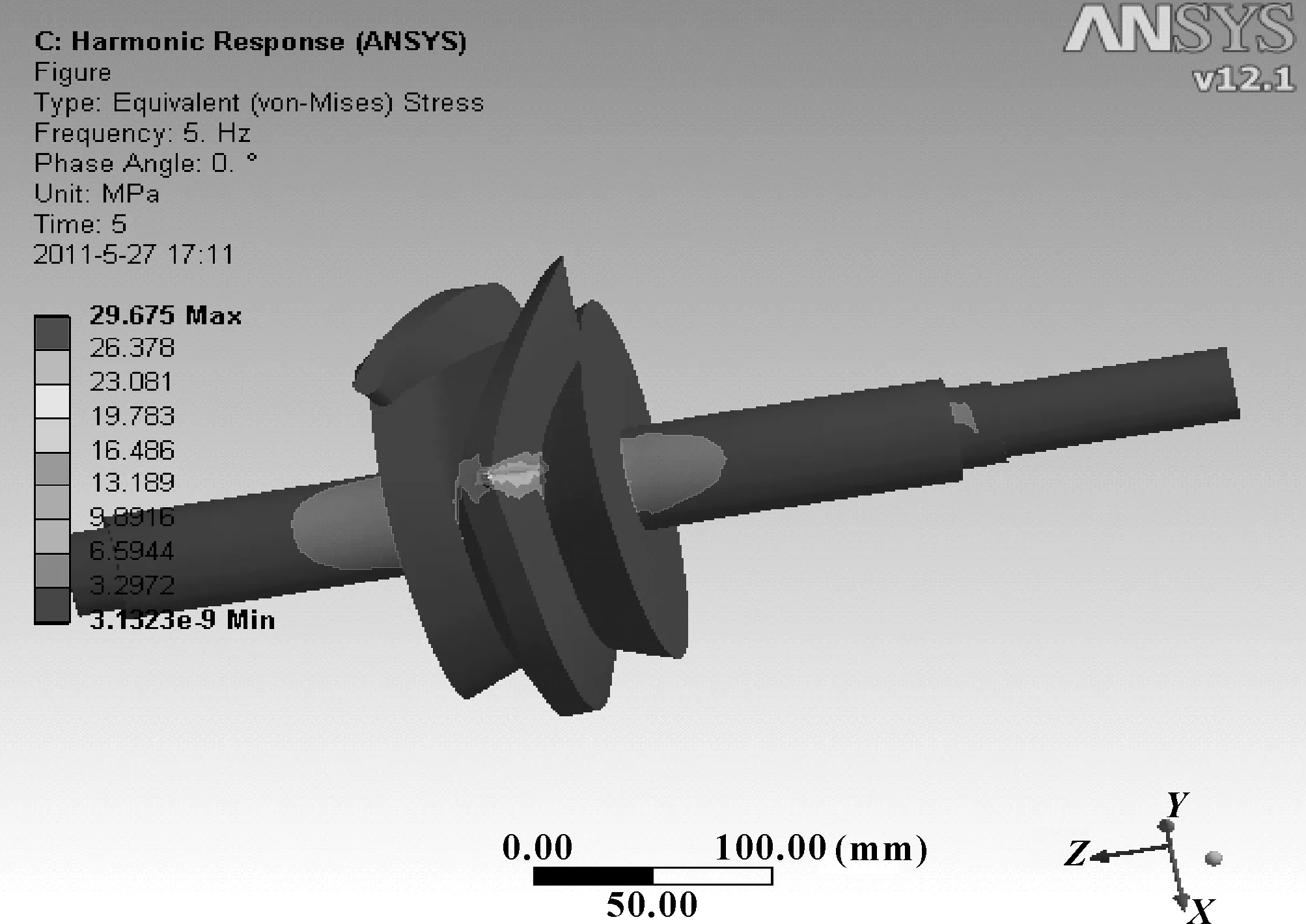
图8 凸轮轴轴向力的响应应力图

项目响应位移/mm响应应力/MPa最大值0.008088629.675

弧面分度凸轮的轴向最大响应位移δ=0.008 043 9 mm,这个变形位移转化为分度盘的转角误差为:

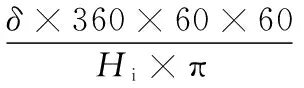
高精度的弧面分度凸轮的分度精度可达到10″～20″。由以上分析得到的变形量大于它的整体分度精度而且这过程还忽略其他误差，所以要对弧面分度凸轮的加工工艺进行改善，充分发挥弧面分度凸轮机构分度精度高特点。从工艺方面入手，可以选择刚性比较好的材料(如38CrMoAl),然后进行热处理提高表面硬度，再进一步也可以研发专用的磨床进行磨削加工。凸轮的接触应力比较小，可以不用重点考虑。

3 结论

利用ANSYS把弧面分度凸轮轴和分度盘轴所受载荷简化为谐载荷，分析了弧面分度凸轮轴在谐载荷作用下的位移响应和应力响应。从谐响应分析结果图可以方便地得到弧面分度凸轮的响应位移和应力变化情况,然后根据位移和压力的变化计算出凸轮轴的分度精度，为高精度凸轮的使用提供理论指导。

[1]李成平,葛正浩,张兴钰，等.基于ANSYS的弧面分度凸轮机构从动件的模态分析[J].机械传动,2015,39(8):145-148.

LI C P,GE Z H,ZHANG X Y,et al.Modal Analysis of Driven Part of Globoid Indexing Cam Mechanism Based on ANSYS[J].Journal of Mechanical Transmission,2015,39(8):145-148.

[2]刘昌祺,牧野洋,曹西京.凸轮机构设计[M].北京：机械工业出版社,2005.

[3]王其超,初嘉鹏.空间分度凸轮机构的通用计算公式[J].机械设计,1995(9)：52-54.

[4]薛风先,胡仁喜,康士廷.ANSYS 12.0机械与结构有限元分析从入门到精通[M].北京：机械工业出版社,2010.

[5]赵韩,OLHOFF N，LAURISTEN S.凸轮机构运动几何学的通用解析公式[J].机械工程学报,1995,31(3):22-26.

[6]刘义,许志沛.机械设计中基于有限元方法的模态分析[J].机械,2003,30(s1):96-98.

LIU Y,XU Z P.The Modal Analysis in Mechanical Design Based of FEM[J].Machinery,2003,30(s1):96-98.

TheHarmonicResponseAnalysisofRollIndexingCamBasedonANSYSWorkbench

GONG Qingshan1，LIU Gang2，WU Yuemin1，ZENG Guohua1

(1.School of Mechanical Engineering, Hubei University of Automotive Technology, Shiyan Hubei 442002,China;2.Zhushan Technical Group School,Shiyan Hubei 442200,China)

The roll indexing cam shaft 3D model was designed with the Pro/E,then the 3D model was imported into ANSYS Workbench.After mesh generation for the roll indexing cam shaft was complete, harmonic response analysis could be done. The influence of the excited force to the indexing accuracy of the roll indexing cam when it worked at high speed was analyzed.All these provide guidance for the application of the high-speed roll indexing cam shaft.

Roll indexing cam shaft; Harmonic response analysis; ANSYS Workbench

2017-05-30

湖北省教育厅科学技术研究项目(Q20171804)

龚青山(1982—)，男，博士研究生，从事绿色制造、装备设计相关研究工作。E-mail:gongqingshan@163.com。

10.19466/j.cnki.1674-1986.2017.10.002

TH112.2

A

1674-1986(2017)10-006-04