一类多维参数高斯过程的弱逼近

李梦玉,申广君,崔 静

(安徽师范大学数学系,安徽芜湖 241000)

一类多维参数高斯过程的弱逼近

李梦玉,申广君,崔 静

(安徽师范大学数学系,安徽芜湖 241000)

本文研究了一类多维参数高斯过程的弱极限问题.在一般情况下,利用泊松过程得到了此类过程的弱极限定理,此多维参数高斯过程可表示为确定的核函数关于维纳过程的随机积分,且包含多维参数的分数布朗运动.

弱收敛;高斯过程;泊松过程;分数布朗运动

1 引言

由于Davydov[8]的工作,最近很多学者研究了布朗运动和分数布朗运动的弱收敛问题.Stroock[13]研究了一维标准的泊松过程与标准的布朗运动之间的如下关系:令{N(t),t≥0}是一个标准的泊松过程,定义

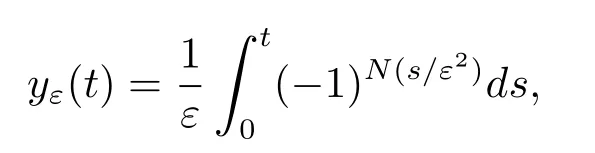
则当ε→0时,yε(t)在连续函数空间C([0,1])中弱收敛到标准的布朗运动{Bt,t≥0}.受到Stroock[13]工作的启发,Bardina和Jolis[2]证明了当ε→0时,随机过程族

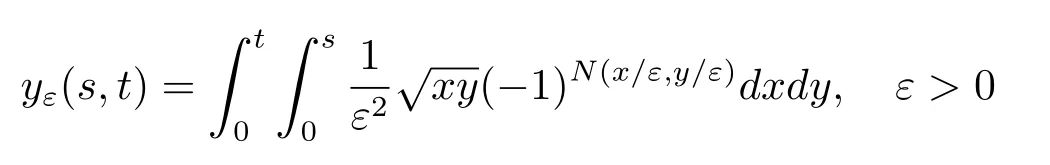
在C([0,1]2)空间中弱收敛到标准的布朗单,其中是平面上的一个标准泊松过程(关于多维情形的相应结果可参考Bardina,Jolis和Rovira[1]).Delgado和Jolis[7]证明了可以利用泊松过程逼近具有如下随机积分表示的一类高斯过程

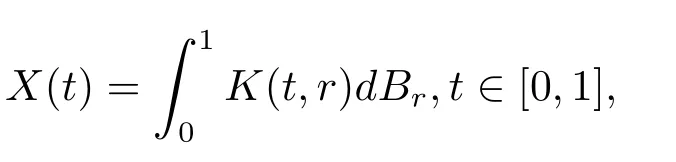
其中K是满足一定条件的确定的核函数.Bardina,Jolis和Tudor[3]把上述结果推广到分数布朗单和其他两参数高斯过程:令使得

其中W={Ws,t,(s,t)∈[0,1]2}是标准布朗单且核函数K1,K2满足一些条件.令

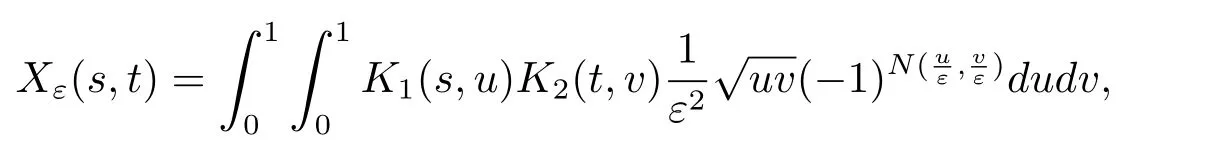
那么Xε在连续函数空间C([0,1]2)中弱收敛到WK1,K2.更多关于分数布朗运动,分数布朗单和多参数过程的相关问题可参见Bardina和Florit[4],Li和Dai[10],Wang等[14,15],徐锐等[16],Dai[6]等文献.

受上述文献的启发,令X(t1,···,td)是具有如下随机积分表示的一类d-维参数高斯过程

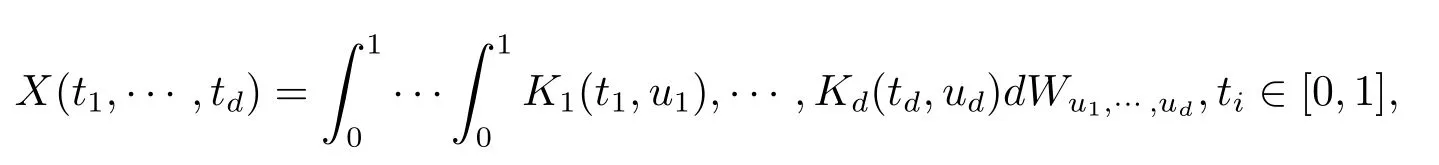
其中W={Wt,t∈[0,1]d}表示d-维布朗运动,Ki,i=1,···,d是满足一定条件的确定的核函数.本文证明了

在连续函数空间C([0,1]d)中弱收敛到X.此结论是将文献[3]中的结论推广到了d-维参数情形,而在多维参数情形下的计算过程会遇到更多的困难,因此更多的借用了文献[1]中的不等式来证明定理.本文中常数C0,C,Cd,cHi,CHi表示常数,在不同的位置可以表示不同的值.

2 主要结论

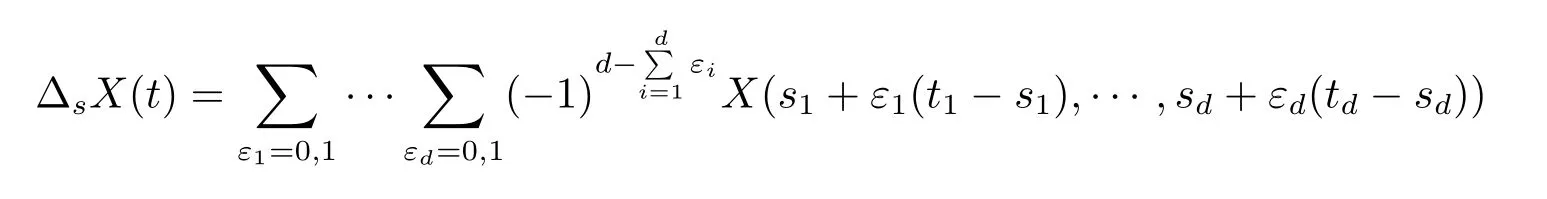
是X在(s,t]上的增量(见Bickel和Wichura[5]).特别地,当d=2时,

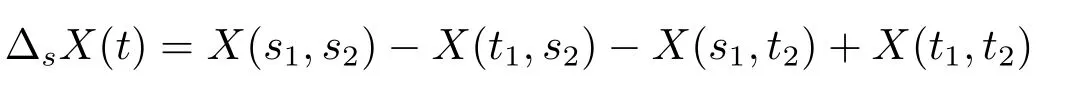
是常见的二维空间上的增量.

本节考虑d-维参数高斯过程X={X(t),t∈[0,1]d},

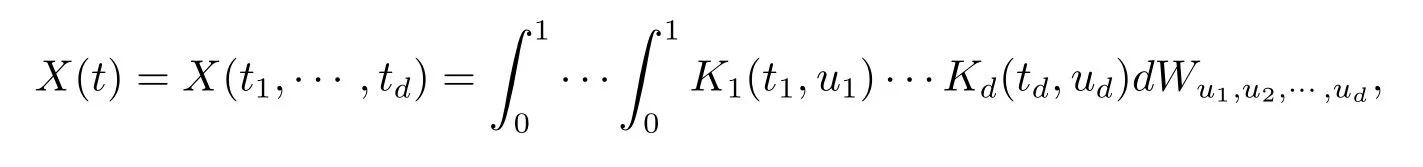
其协方差函数为

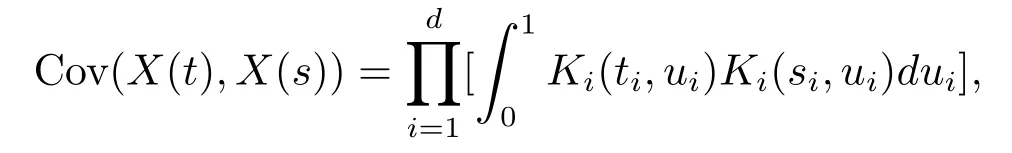
其中Ki:[0,1]×[0,1]→R是满足下列条件的函数:

(H1)(i)对i=1,2,···,d,Ki是可测的且对任意的ui∈[0,1],Ki(0,ui)=0,a.e..

(ii)对i=1,2,···,d,存在单增的连续函数Fi:[0,1]→R和αi＞1使得对任意0≤si＜ti≤1,有

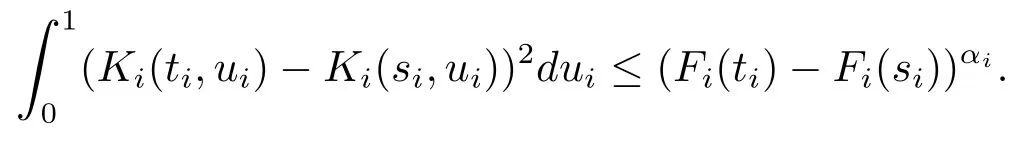
(H2)(i)对i=1,2,···,d,Ki是可测的且对任意的ui∈[0,1],Ki(0,ui)=0,a.e..

(ii)’对i=1,2,···,d,存在单增的连续函数Fi:[0,1]→R和0＜ ρi≤1使得对任意0≤si＜ti≤1,有

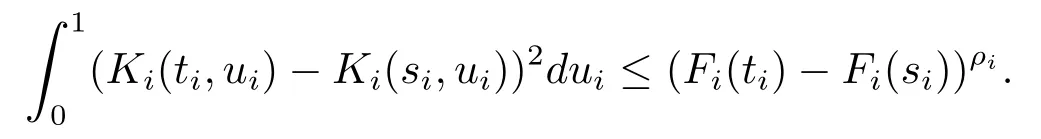
(iii)对i=1,2,···,d,存在常数Mi＞0和βi＞0使得对任意的0≤si＜ti≤1和0≤s0i＜t0i≤1,

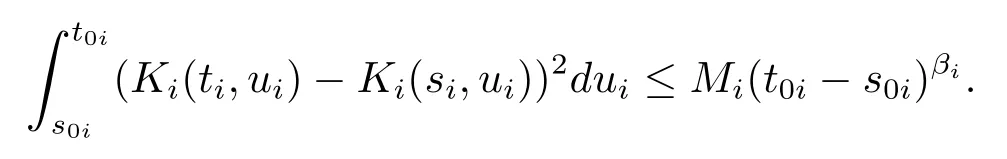
注意到条件(ii)较(ii)’强,在较弱的条件(ii)’下增加条件(iii)是为了证明Xn的胎紧性.

令{N(x),x∈Rd+}是定义在概率空间(Ω,F,P)上的标准泊松过程,∀n＞0,ti∈[0,1],i=1,2,···d,定义

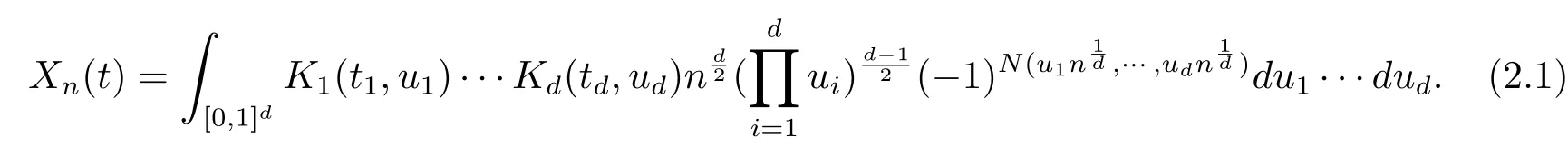
本节将证明在连续函数空间C([0,1]d)中,当n→∞时,Xn弱收敛到X.为了简化记号,用Nn(u)表示随机变量则Nn是强度为n的泊松过程.

为了证明主要结果,首先给出如下引理.引理2.1说明了过程Xn是连续的.

引理2.1设θ∈L∞([0,1]d),定义

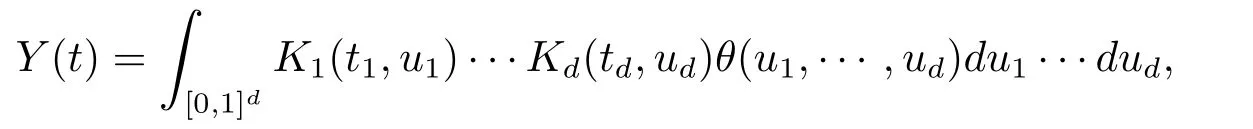
其中核函数Ki,i=1,2,···,d满足条件(i)和(ii)’,那么Y(t)是一个连续函数.

证∀0＜si≤ti＜1,i=1,···,d,根据Hölder不等式和条件(ii)’有

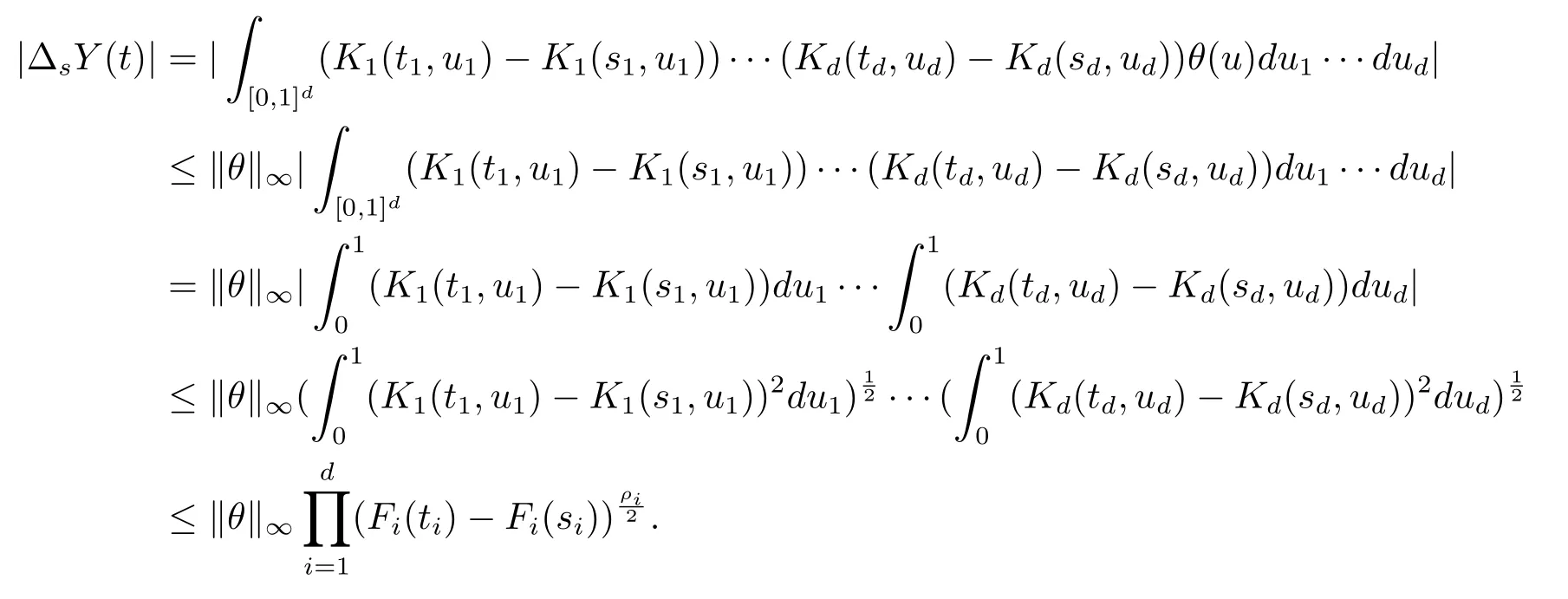
再由条件(i)知Y(t)是一个连续函数.

引理2.2对任意函数fi∈L2([0,1]),i=1,2,···,d,存在一个正常数Cd使得

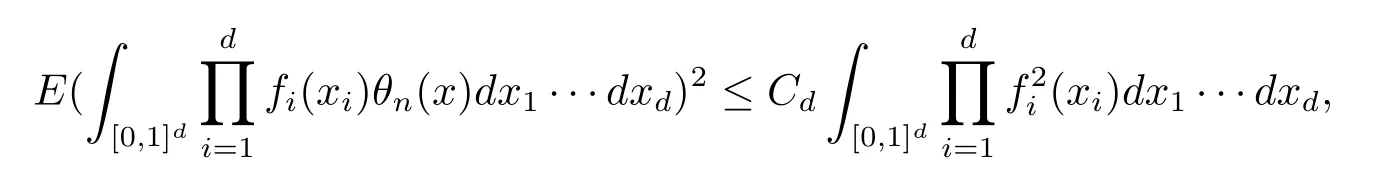
其中

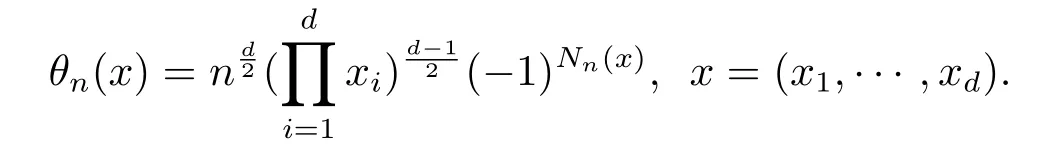
证由于(见参考文献[1])

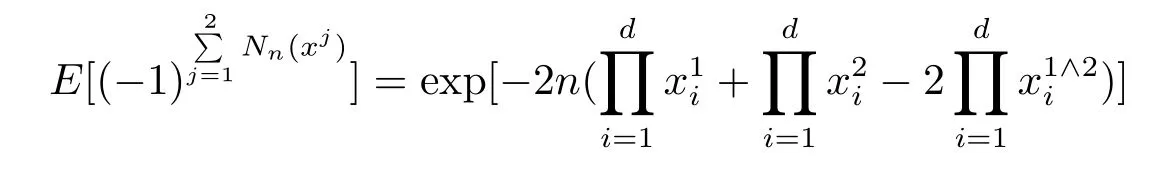
和

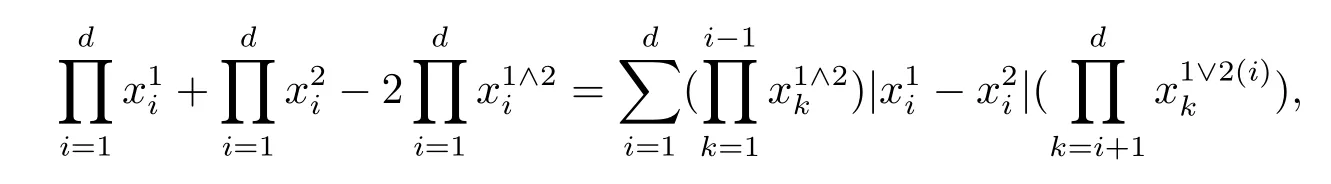
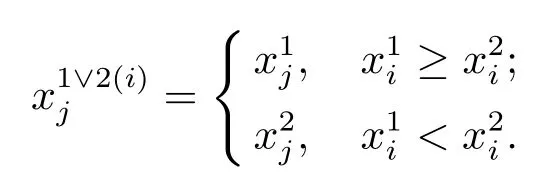
进而有

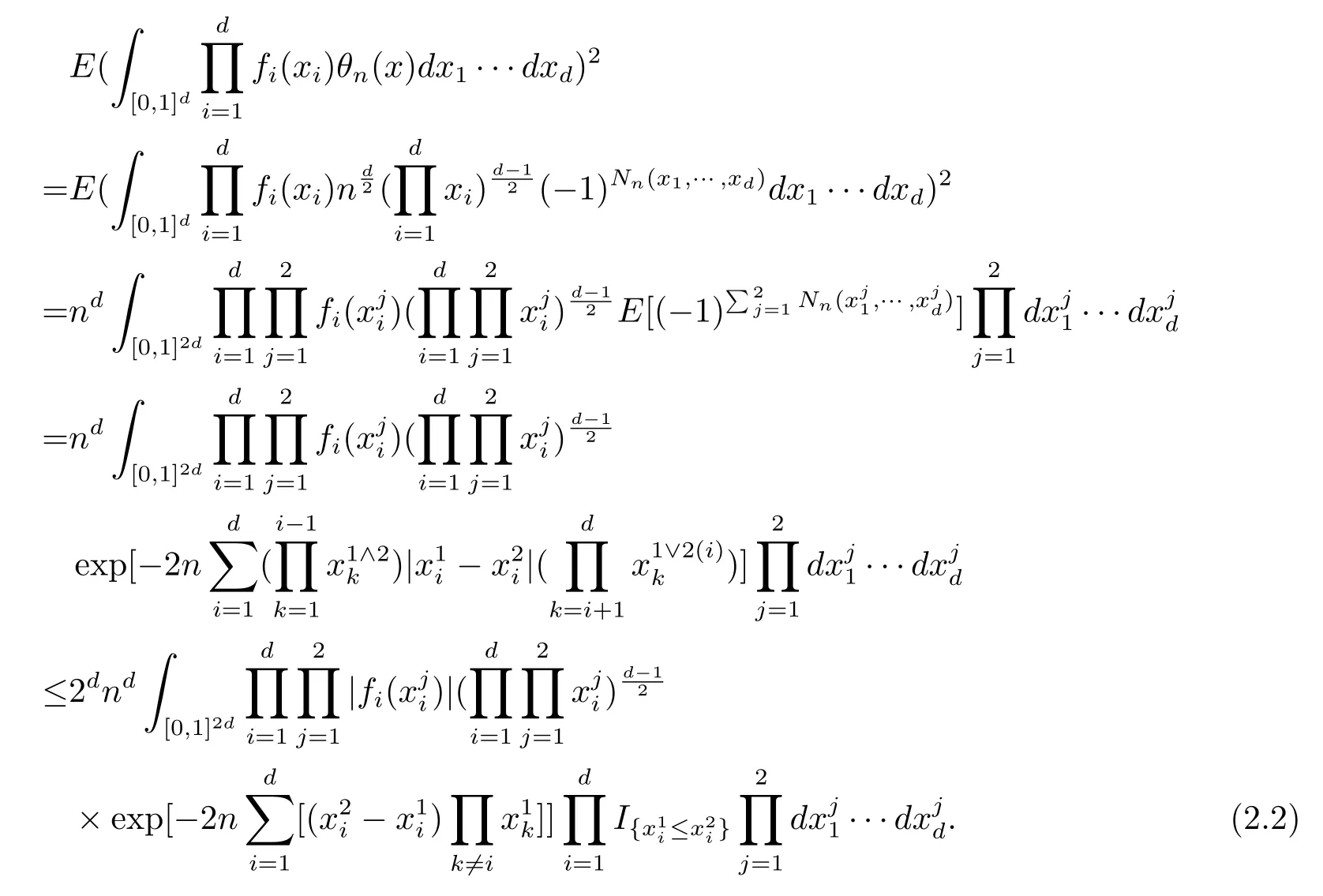
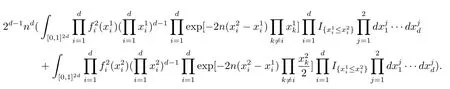
又有

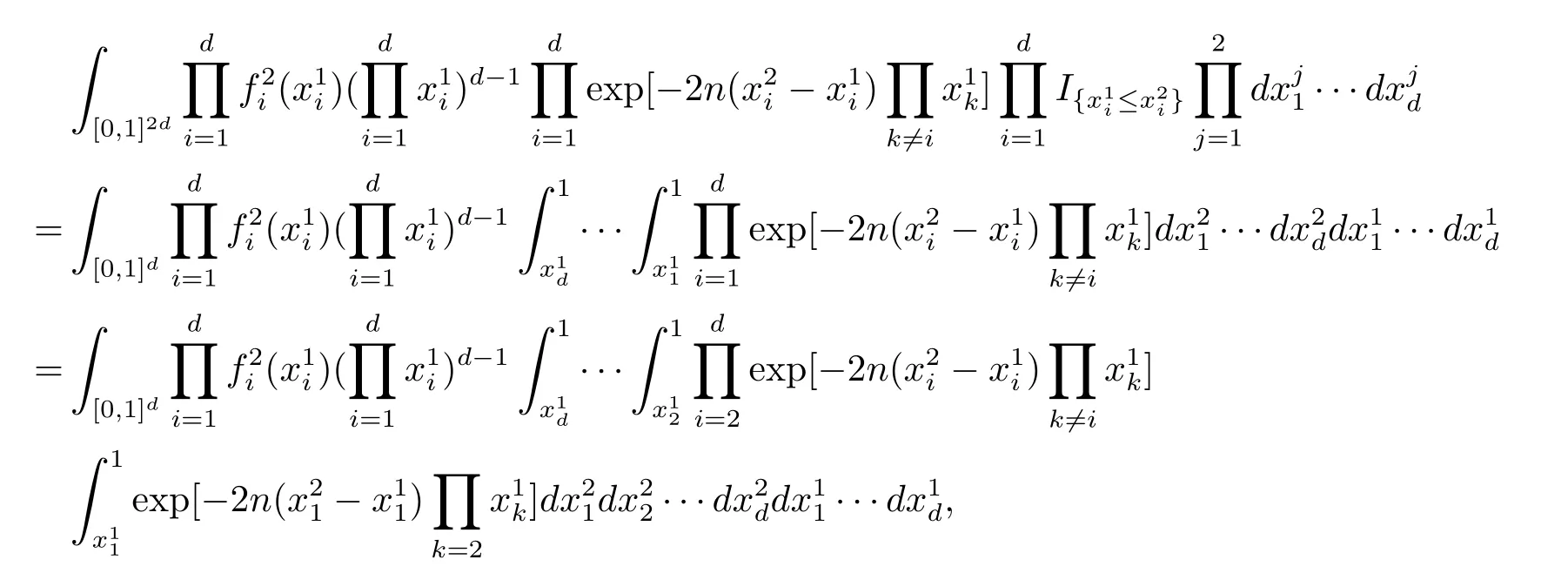
其中

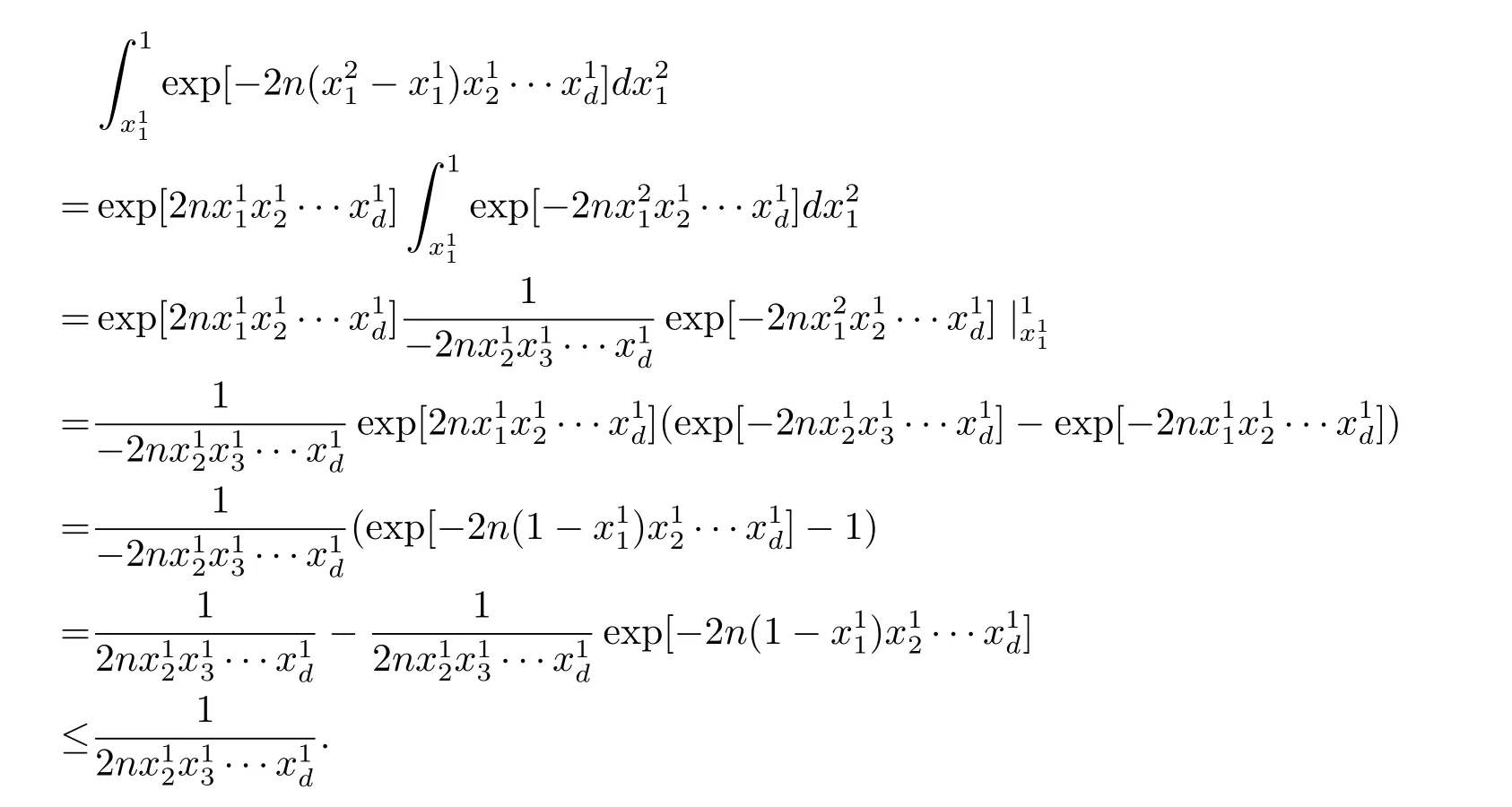
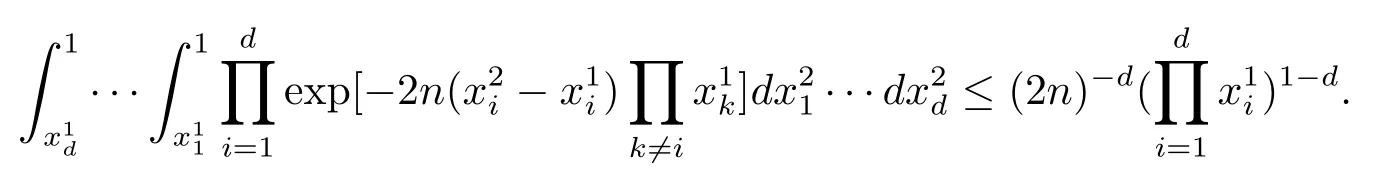
故

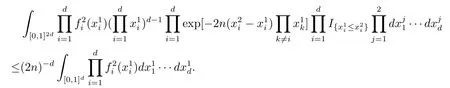
同理可计算

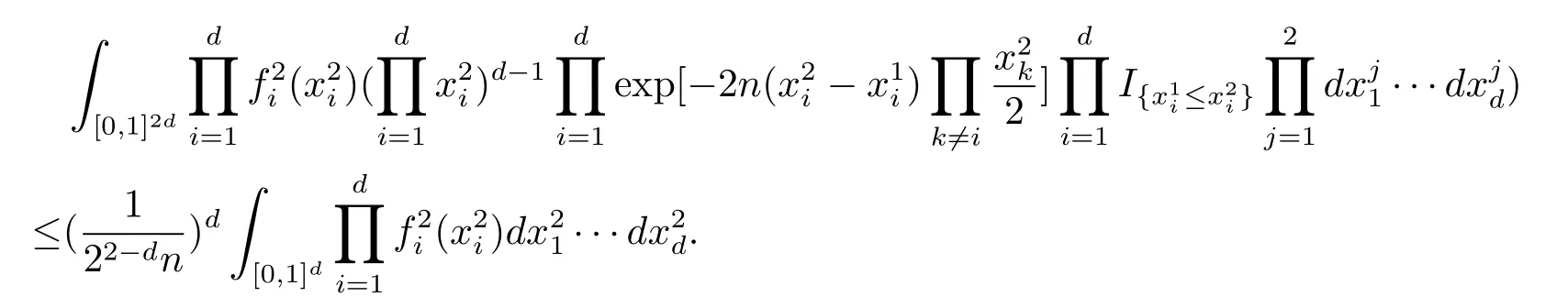
综上可得

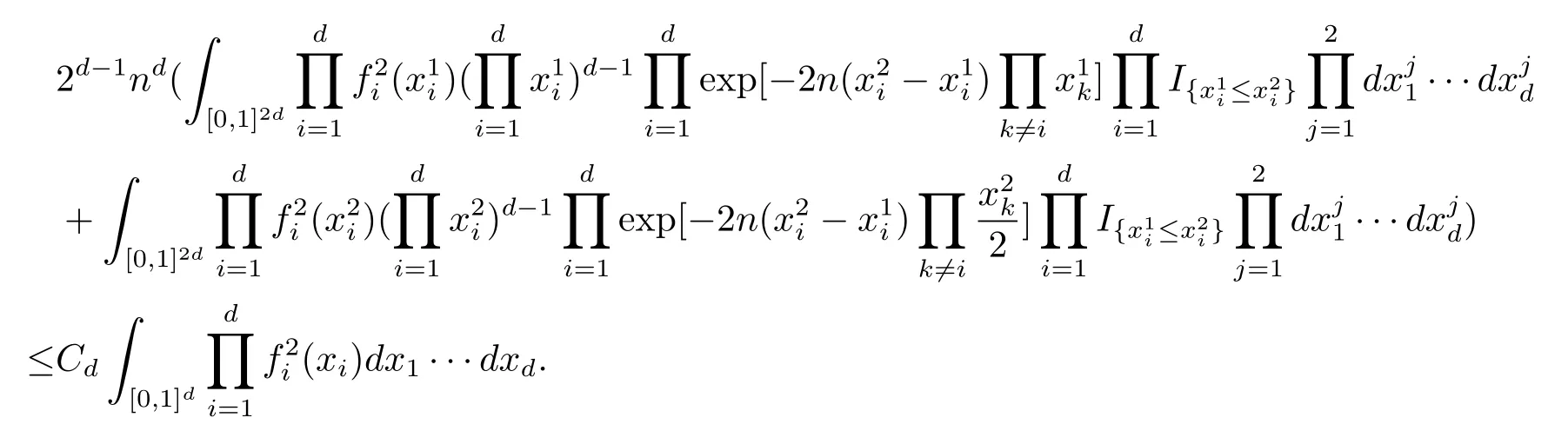
下面计算表达式(2.2)在区域Ac上的积分.Ac可分解成如下区域的并

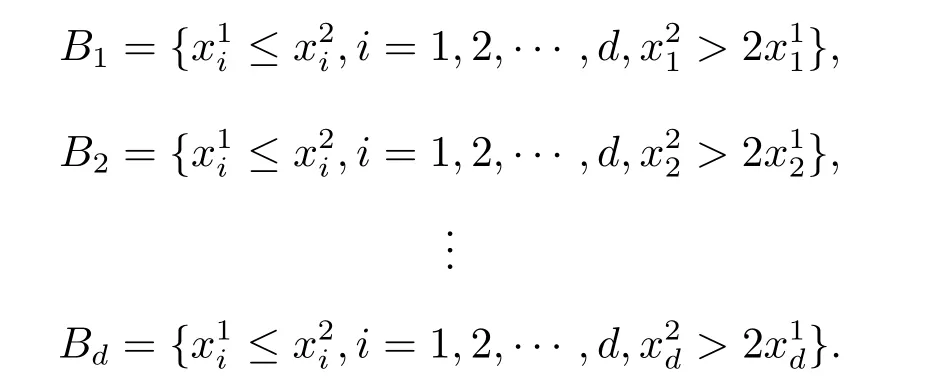
仅计算在B2上的积分,其它区域上的积分可以类似计算.在B2上有不等式

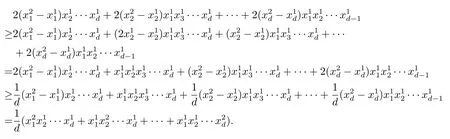
因此表达式(2.2)在B2上的积分就可以用下面的式子来控制

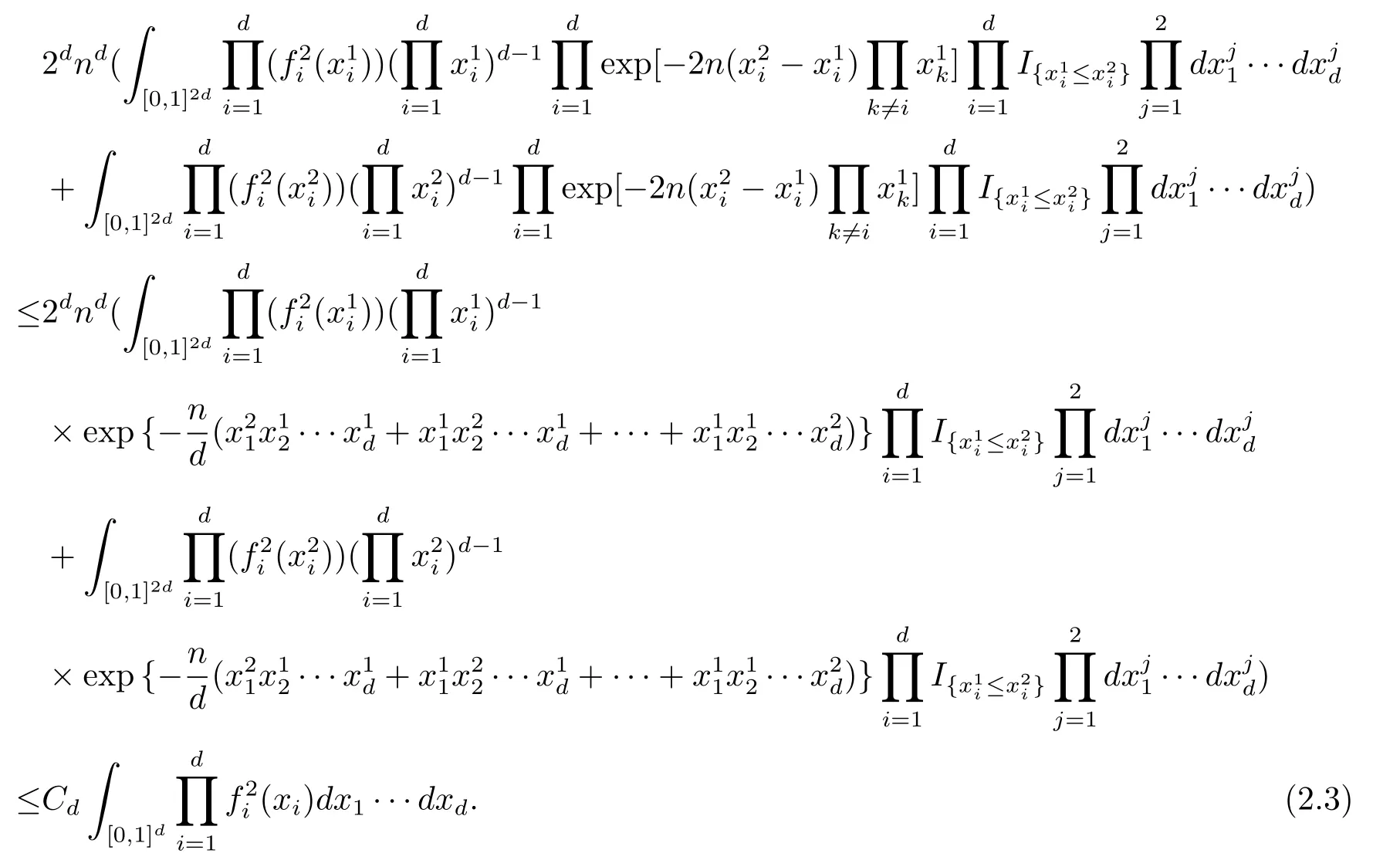
事实上

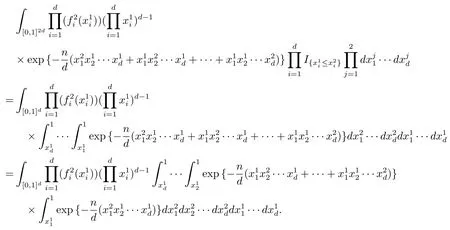
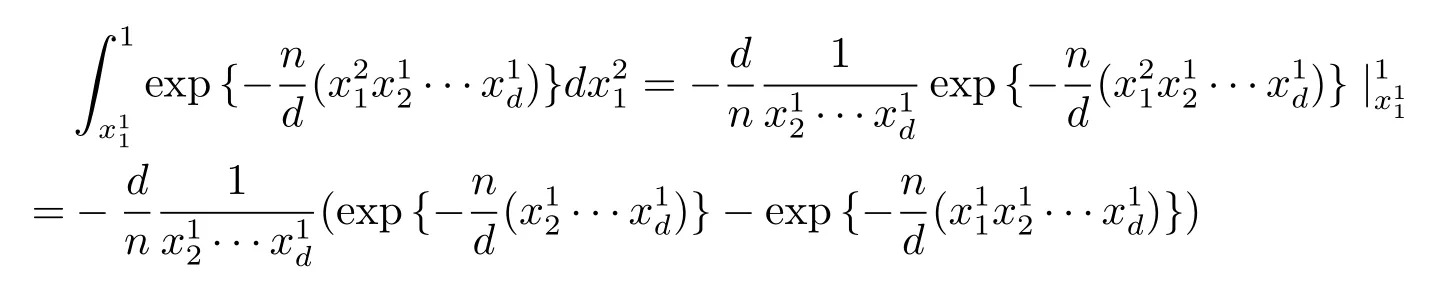
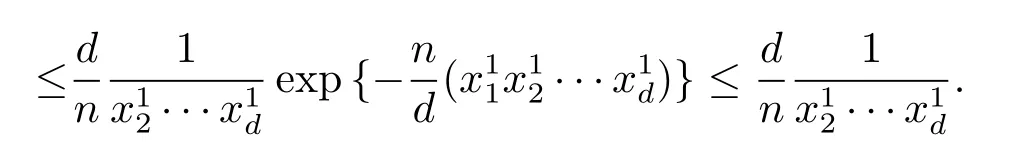
同理可计算

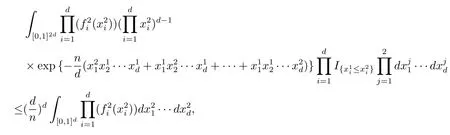
故(2.3)式成立.综上,可以得到

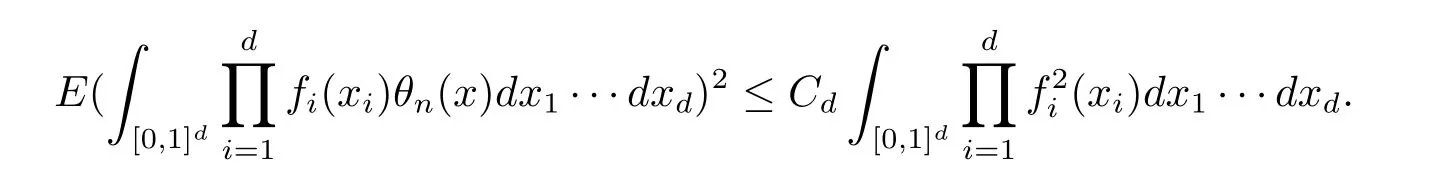
引理2.3设Y={Y(s),s∈[0,1]d}是一个连续过程.假设对固定的偶数m∈N和δi∈(0,1),i=1,2,···,d存在常数L＞0使得对任意的0＜si＜ti＜2si,i=1,2,···,d,有

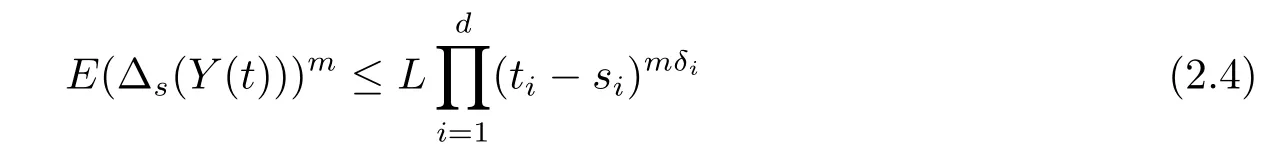
成立.那么存在一个仅依赖于m和δi,i=1,2,···,d的常数C使得对任意的0≤si＜ti≤1,i=1,2,···,d,有成立.

证易证过程Y满足

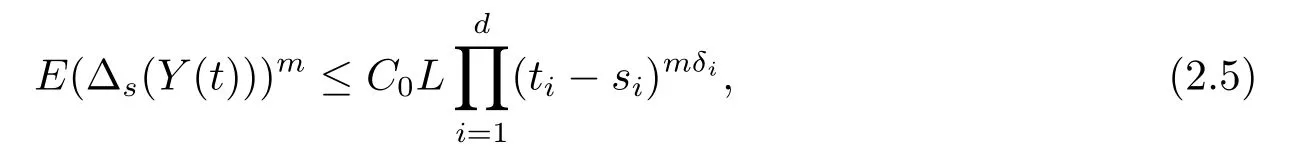
其中C0是依赖于m和δi,i=1,2,···,d的常数.

下面把区间(si,ti]分解成可数个互不相交的小区间的和

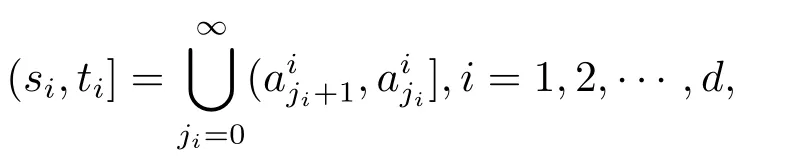
根据Y的连续性有

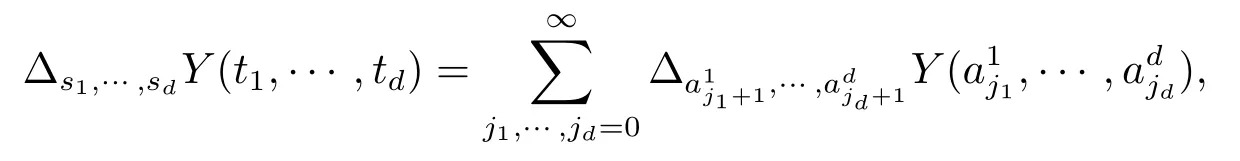
且上式右边的每个增量均满足(2.5)式.所以

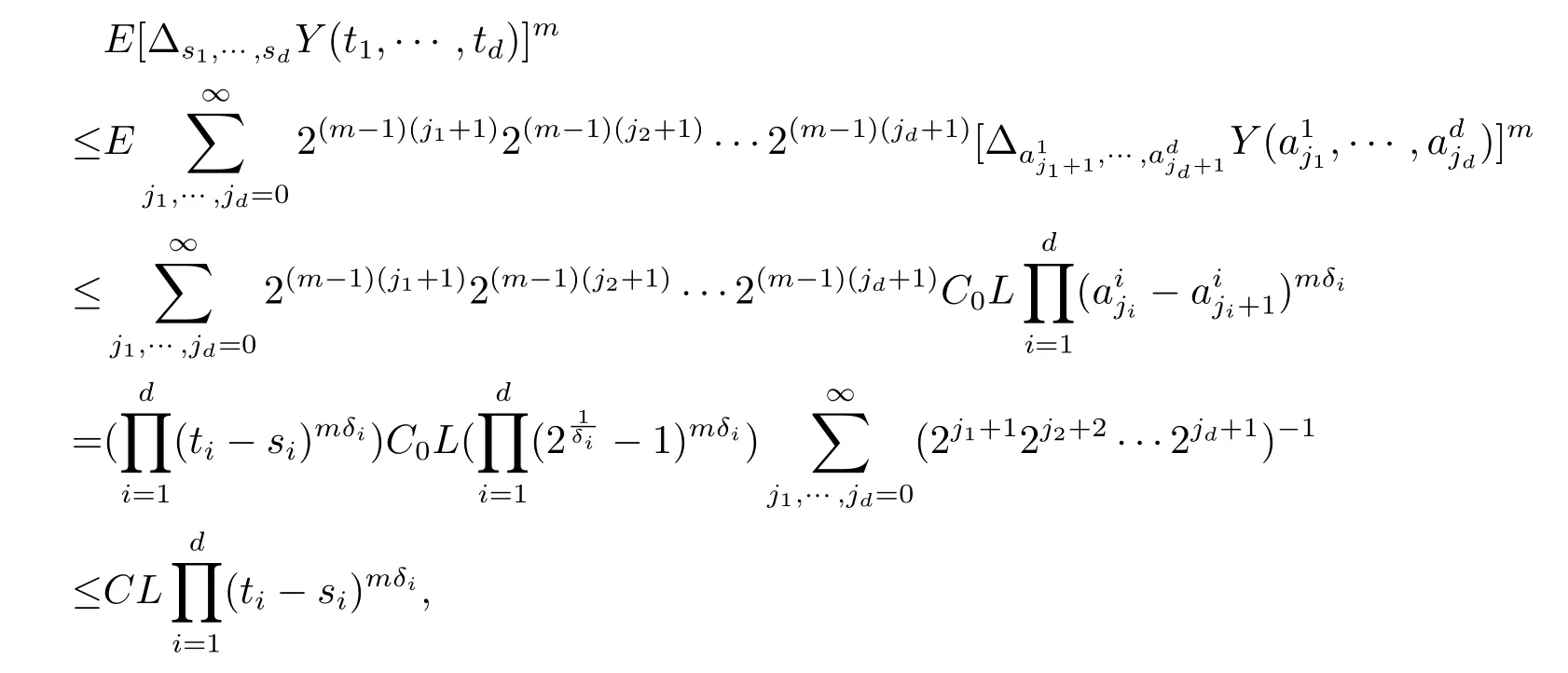
其中第一步使用了不等式

引理2.4设Xn是(2.1)式中定义的随机过程,核函数Ki,i=1,2,···,d满足条件(H2),那么对任意的偶数m∈N,存在仅依赖于m和条件(iii)中出现的参数的常数C,使得对任意

证

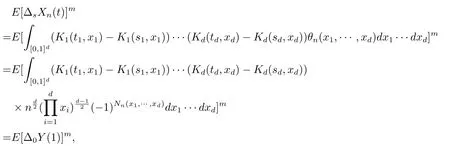
其中

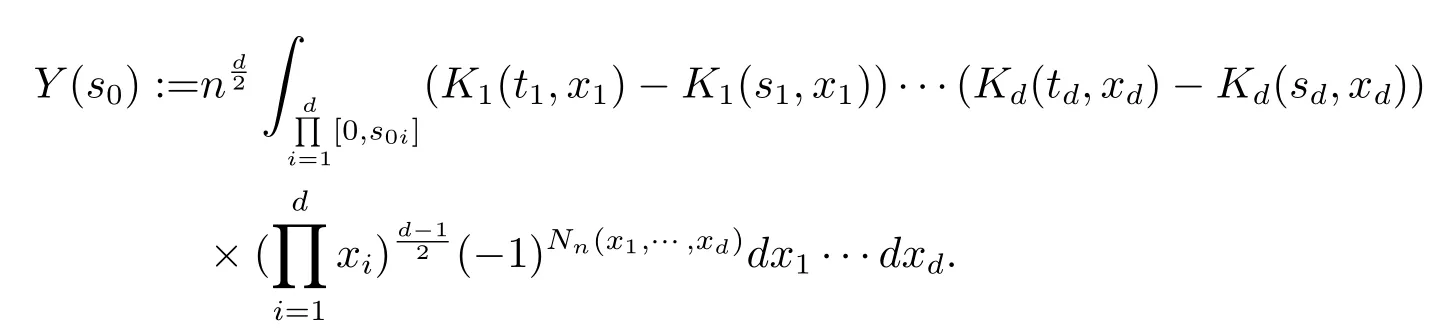
根据引理2.3,只需要证明对任意的0＜s0i＜t0i＜2s0i,i=1,2,···,d,有

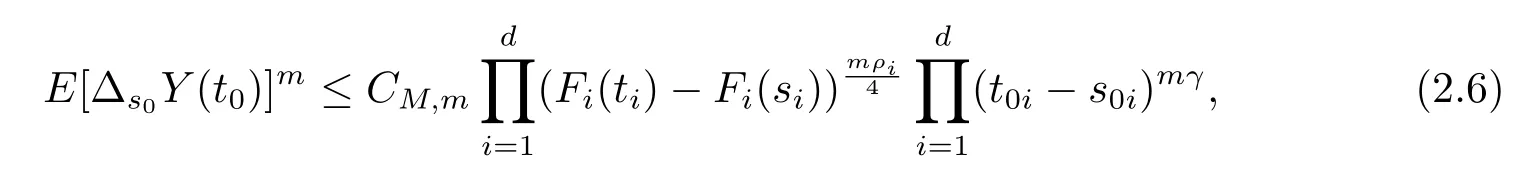
事实上

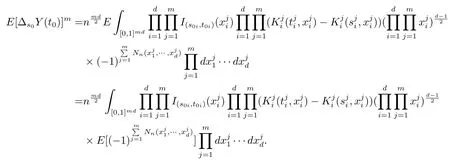
注意到

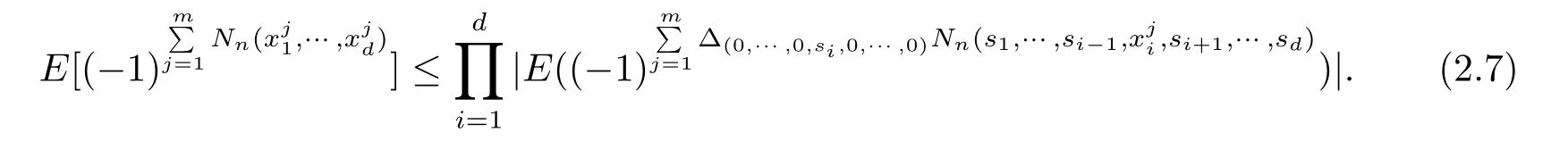
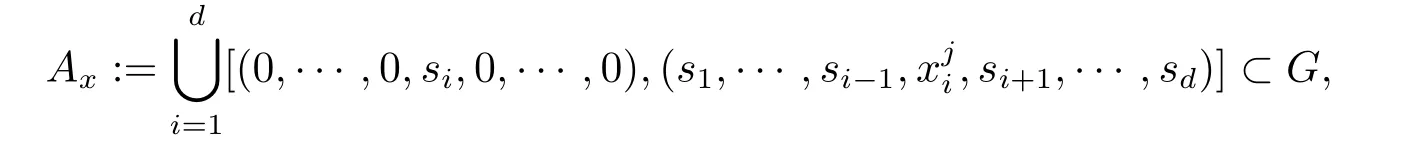
这里

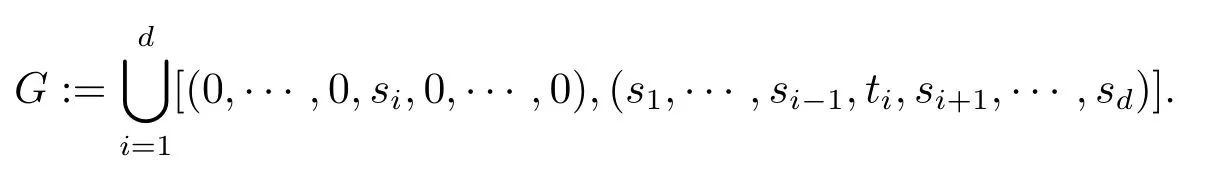
进一步Bx⊂Gc.给定xj,j=1,2,···,m,那么和是互不相交的.所以相关的增量也是独立的,故易得到(2.7)式.

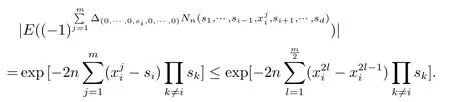
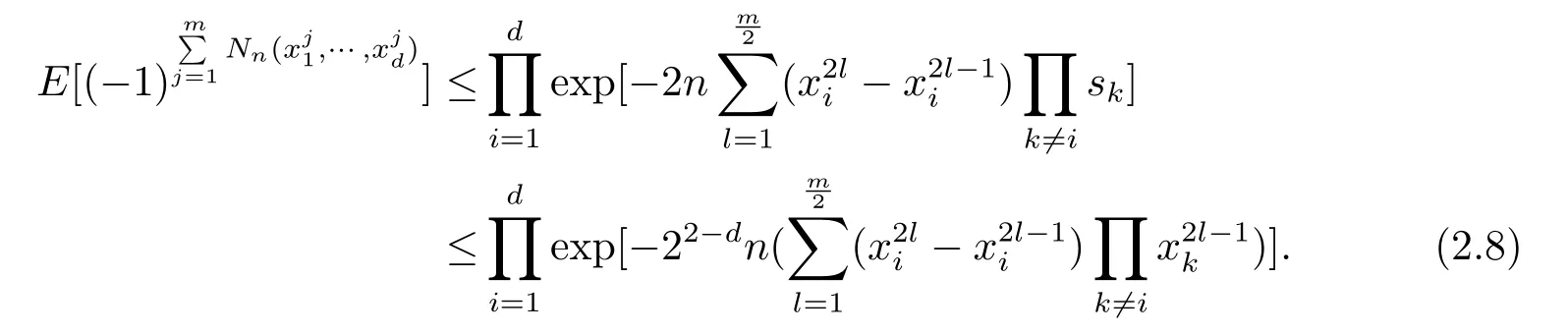
因此根据(2.8)式可得

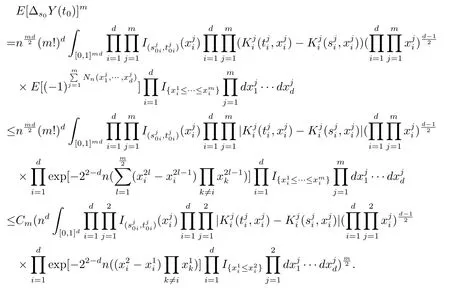
由引理2.2的计算过程可类似计算上式不超过

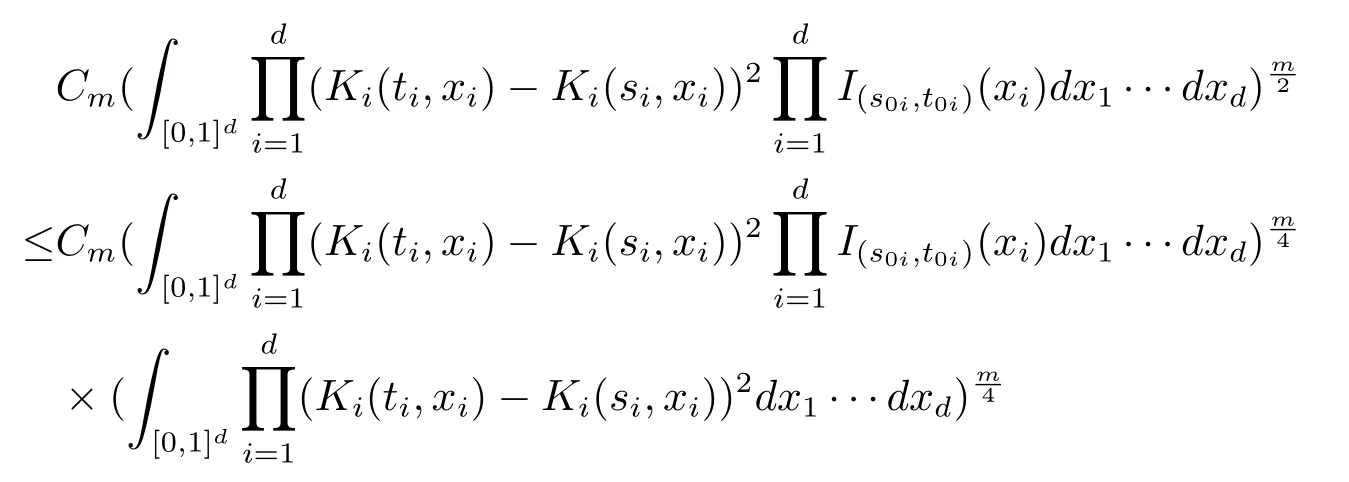
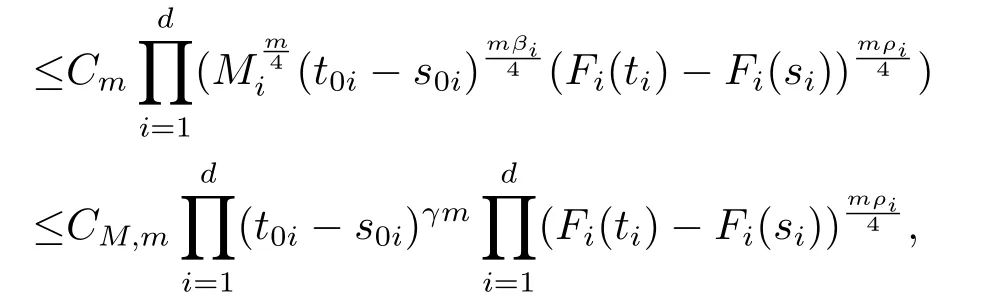
定理 2.5在(H1)或(H2)的条件下,当n→∞时,(2.1)式定义的随机过程族{Xn(t),t∈[0,1]d}在连续函数空间C([0,1]d)中弱收敛到X.

证首先,证明随机过程族{Xn}的胎紧性.由于{Xn}在坐标轴上取值为零,利用Bickel和Wichura[5]中建立的关于多参数随机过程的胎紧性准则,只需证明对某些m≥2存在常数C＞0和η＞1,以及单增的连续函数Fi,i=1,2,···,d,使得对0≤si≤ti≤1,i=1,2,···,d,

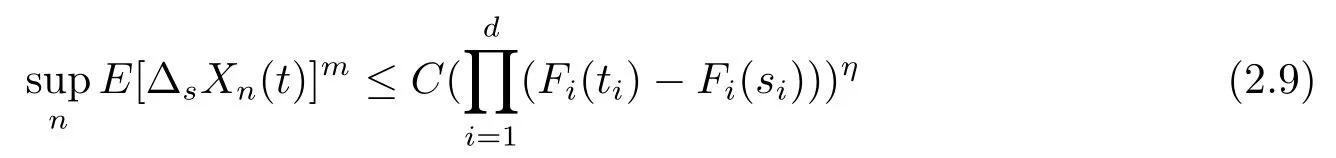
成立即可.

假设条件(H1)成立,根据引理2.2和条件(ii)有

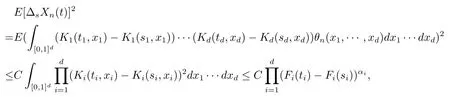
其中第一个不等式使用了引理2.2,αi＞1,i=1,2,···,d.即(2.9)式成立.

假设条件(H2)成立.根据引理2.4,对任意的偶数m∈N存在一个常数C使得对0≤si≤ti≤1,i=1,2,···,d时,有成立,即(2.9)式成立.

其次,证明随机过程Xn依有限维分布收敛到X.事实上,只要证明∀k≥1,a1,···,ak∈R且当n→∞时,随机变量列依分布收敛到等价的只要证明相应的特征函数收敛即可.

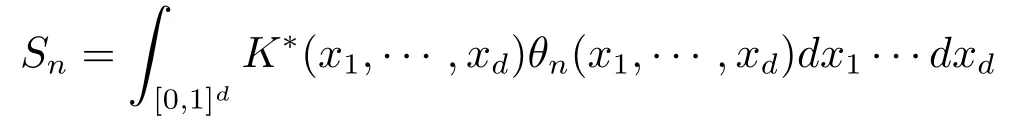
和

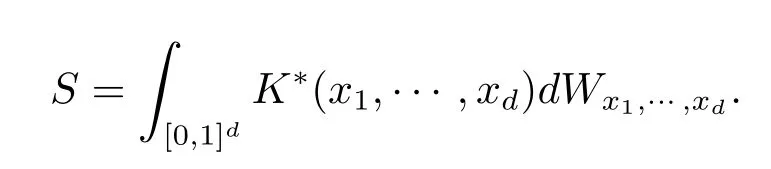
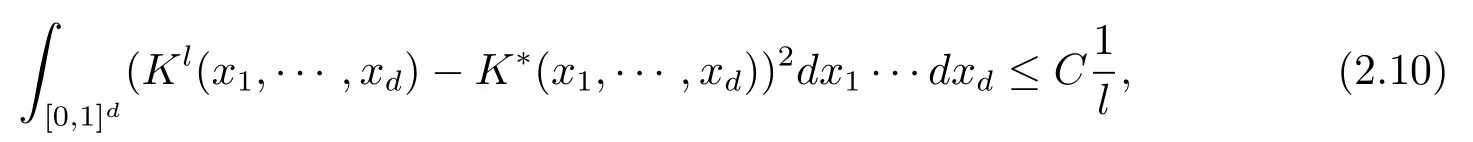
定义

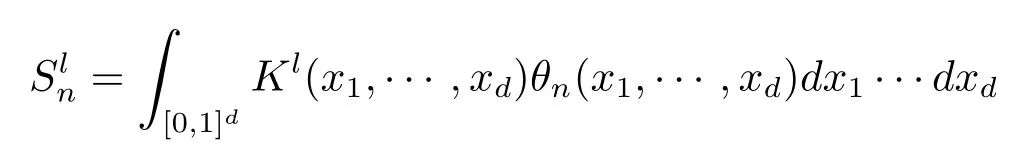
另一方面,根据Bardina,Jolis和Rovira[1],当n→∞时,

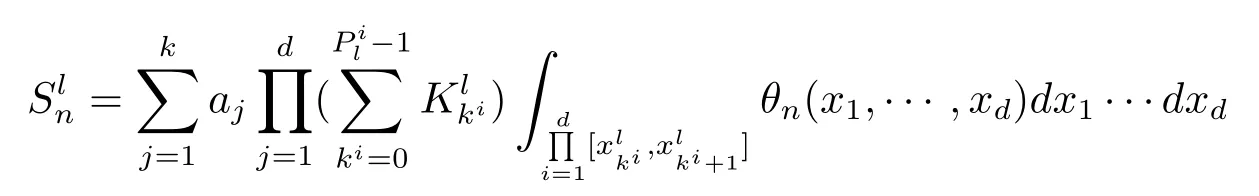
依分布收敛到

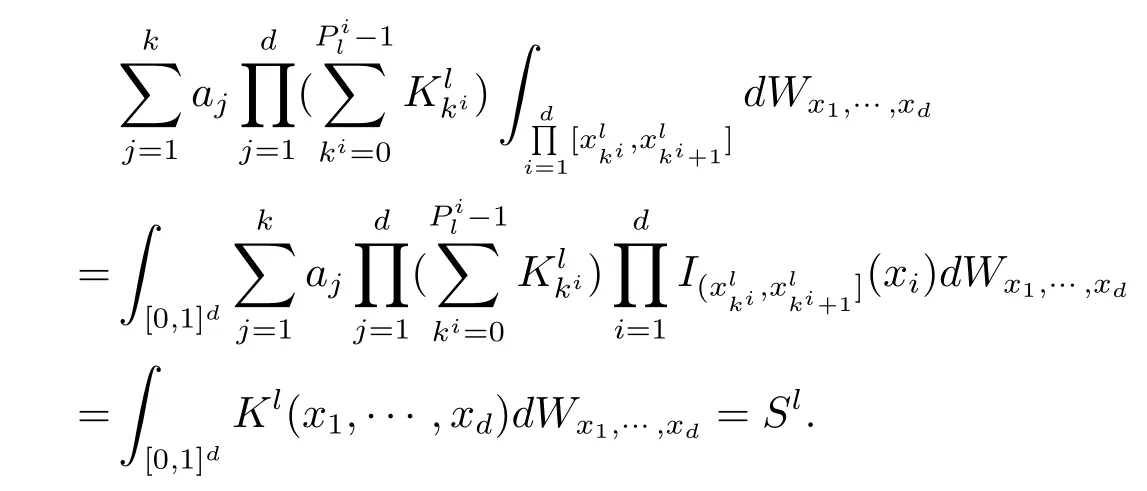
因此∀x∈R和l∈N,有

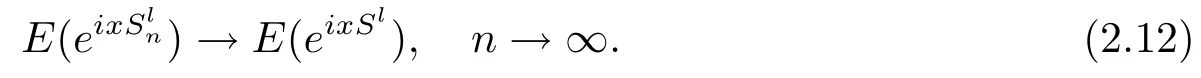
最后∀x∈R和l,n∈N,|E[eixSn]−E[eixS]|≤η1+η2+η3,其中

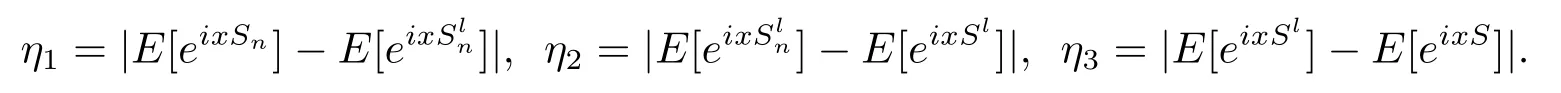
联立(2.11)式以及对t∈R,可以得到

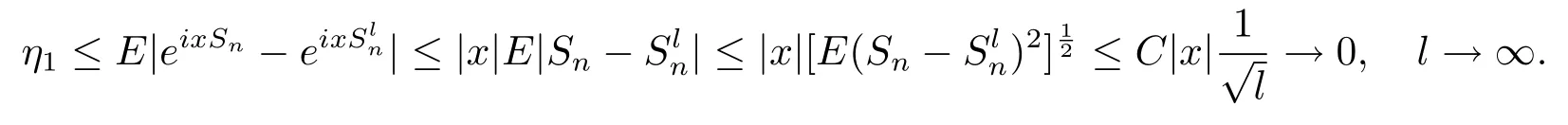
根据(2.12)式,当n→∞时,η2→0.根据(2.10)式和多重随机积分的性质有

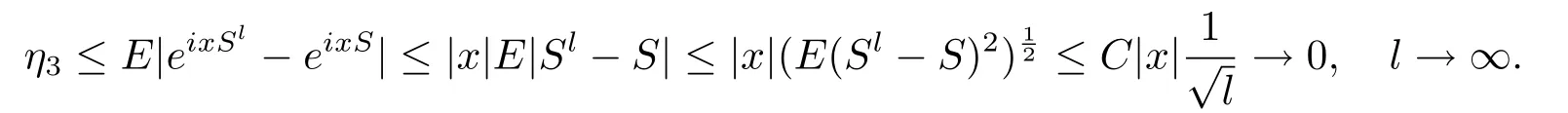
综上,定理得证.

3 例子:多维参数分数布朗单

基于Mandelbrot和Van Ness[11]的工作,分数布朗运动受到越来越多学者的关注,现已广泛应用于金融、通讯等领域,它是具有自相似、长相依、平稳增量的高斯过程,其协方差函数为

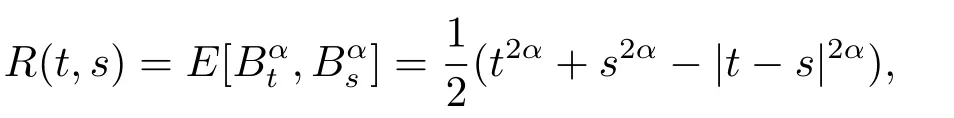
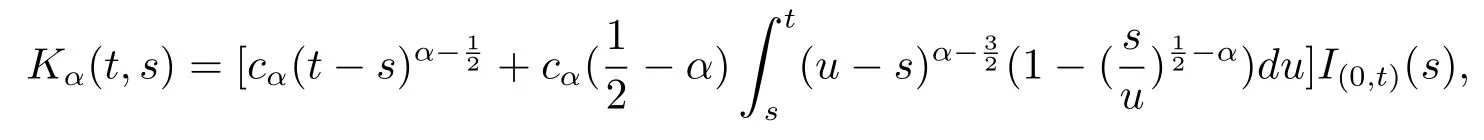
其中

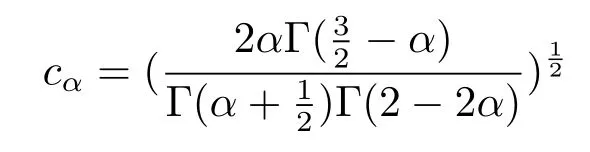
是一个标准化的常数.

作为分数布朗运动的扩张过程,d维分数布朗单是定义在概率空间(Ω,F,P)上的中心高斯过程且协方差函数其中当是标准的d维布朗单它有连续的样本轨道且在坐标轴上为零,具有如下积分表示

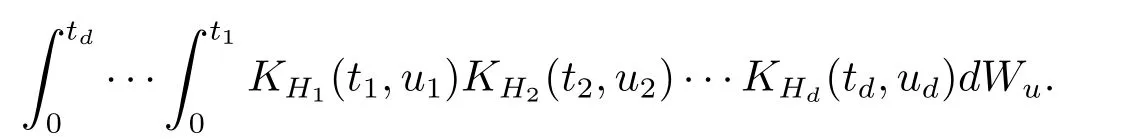
以下验证d维分数布朗单满足本文中的假设条件.

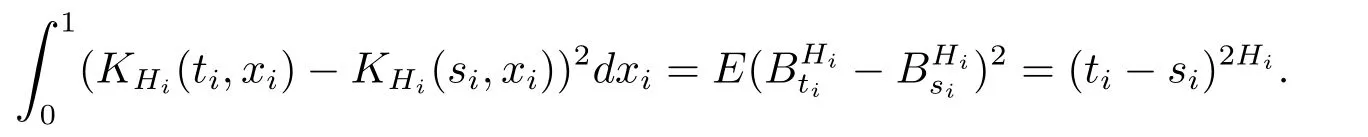
此时取Fi(x)=x,αi=2Hi,则核函数KHi,i=1,2,···,d满足条件(H1).

核函数KHi,i=1,2,···,d也满足条件(H2).事实上只需要验证核函数满足条件(iii).

对任意的a,b,z,|z|＞1且任意的c≠0,−1定义高斯超几何函数F(a,b,c,z)如下(详见参考文献[12])

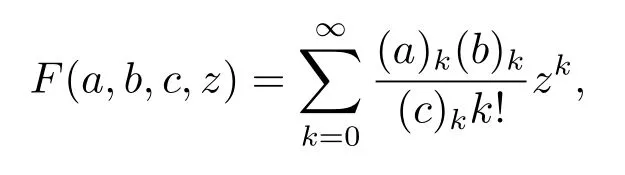
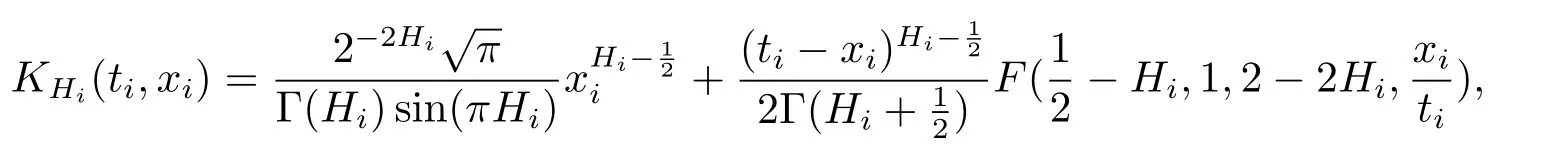
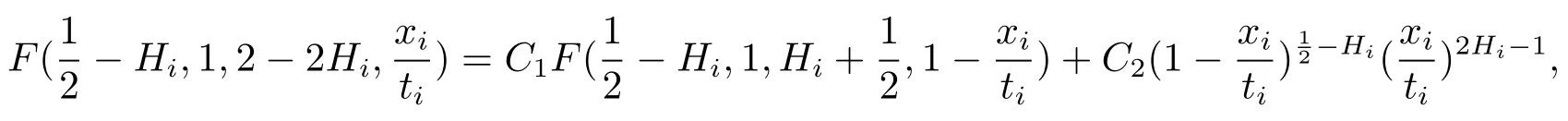
其中C1,C2是常数.在超几何函数中因为所以在上关于xi是连续的. 因此在时,在[0,ti]上关于xi是连续的,故在[0,ti]上存在常数C′使得即同理存在C′′使得所以∀si＜ti,i=1,2,···,d,有其中C取C′和C′′中较大者.因此对s0i＜t0i,有

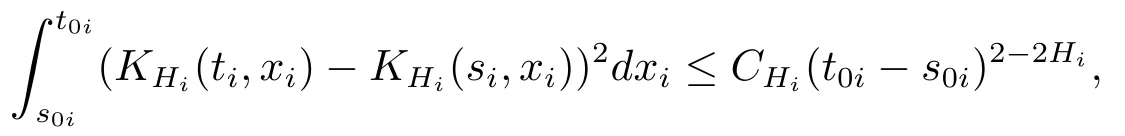
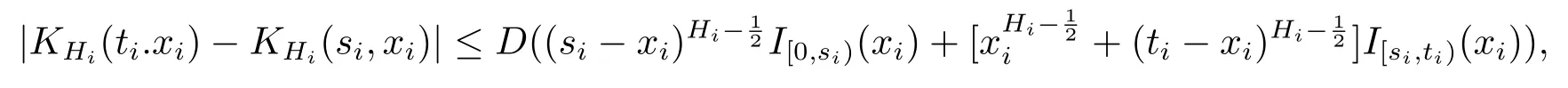
其中D取d′和d′′中较大者.所以∀s0i＜t0i,i=1,2,···,d,

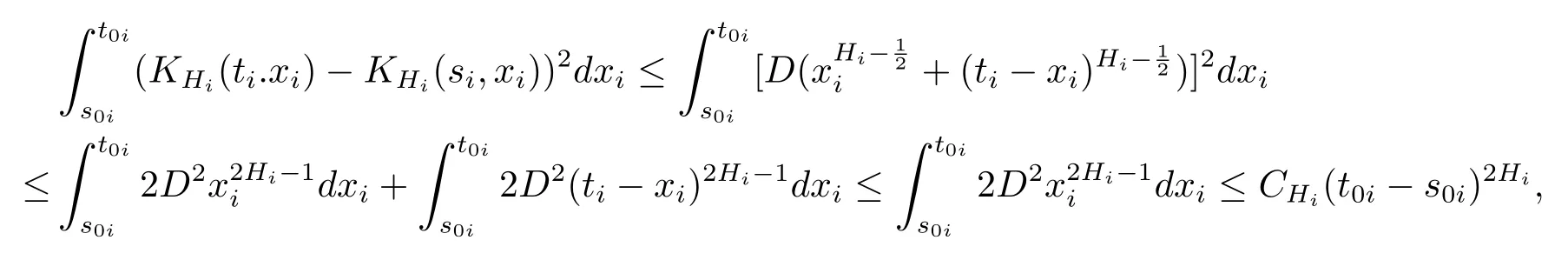
[1]Bardina X,Jolis M,Rovira C.Weak approximation of the Wiener process from a Poisson process:the multidimensional parameter set case[J].Stat.Prob.Lett.,2000,50(3):245–255.

[2]Bardina X,Jolis M.Weak approximation of the Brownian sheet from the Poisson process in the plane[J].Intern.Stat.Insti.Bernoulli Soc.Math.Stat.Prob.,2000,6(4):653–665.

[3]Bardina X,Jolis M,Tudor C.Weak convergence to the fractional Brownian sheet and other twoparameter Gaussian process[J].Stat.Prob.Lett.,2003,65(4):317–329.

[4]Bardina X,Florit C.Approximation in law to thed-parameter fractional Brownian sheet based on the functional invariance principle[J].Rev.Mate.Iberoamericana,2005,21(3):1037–1052.

[5]Bickel P,Wichura M.Convergence criteria for multiparamenter stochastic process and some applications[J].Ann.Math.Stat.,1971,42(5):1656–1670.

[6]Dai H.Convergence in law to operator fractional Brownian motions[J].J.Theor.Prob.,2013,26(3):676–696.

[7]Delgado R,Jolis M.Weak approximation for a class of Gaussian process[J].J.Appl.Prob.,2000,37(2):400–407.

[8]Davydov Y.The invariance principle for stationary processes[J].The.Prob.Appl.,1970,15(3):498–509.

[9]Decreusefond L,Üstünel A S.Stochastic analysis of the fractional Brownian motion[J].Potent.Anal.,2010,10(2):177–214.

[10]Li Y,Dai H.Approximations of fractional Brownian motion[J].Bernoulli,2011,17(17):1195–1216.

[11]Mandelbrot B B,Van Ness J W.Fractional Brownian motion,fractional noises and applications[J].Soc.Indus.Appl.Math.,1968,10(4):422–437.

[12]Nokiforov A F,Uvarov V B.Special functions of mathematical physics[M].Boston:Birkhäuser Basel,1988.

[13]Stroock D.Topics in stochastic differential equations[M].Berlin:Tata Insti.Funda.Res.Bomb.,1982.

[14]Wang Z,Yan L,Yu X.Weak approximation of the fractional Brownian sheet from random walks[J].Elec.Commun.Prob.,2013,18:1–13.

[15]Wang Z,Yan L,Yu X.Weak approximation of the fractional Brownian sheet using martingale differences[J].Stat.Prob.Lett.,2014,92:72–78.

[16]徐锐,祝东进,申广君.多参数双分数布朗运动相遇局部时的存在性和联合连续性[J].数学杂志,2015,35(6):1411–1423.

WEAK APPROXIMATION FOR A CLASS OF MULTIDIMENSIONAL PARAMETER GAUSSIAN PROCESS

LI Meng-yu,SHEN Guang-jun,CUI Jing
(Department of Mathematics,Anhui Normal University,Wuhu 241000,China)

In this paper,we study the weak convergence problem of a multidimensional parameter Gaussian process.Under rather general conditions,we give an approximation in law of the process which can be represented by a stochastic integral of a deterministic kernel with respect to a standard Wiener process. The approximation processes are constructed from a standard Poisson process.An example of a Gaussian process to which this result applies is the multidimensional parameter fractional Brownian sheet with any Hurst parameter.

weak convergence;Gaussian process;Poisson process;fractional Brownian motion

60F05;60G18

O211.4

A

0255-7797(2017)06-1287-16

2015-06-03接收日期:2016-05-16

国家自然科学基金(11271020;11401010);安徽省杰出青年科学基金(1608085J06);安徽省自然科学基金(1408085MA07).

李梦玉(1990–),女,安徽六安,硕士,主要研究方向:随机过程与随机分析.

申广君.