抛物型Monge-Ampère型方程的Cauchy-Neumann问题
2017-11-06张俊玮
向 妮,吴 燕,窦 楠,张俊玮
(湖北大学数学与统计学学院,湖北武汉 430062)
抛物型Monge-Ampère型方程的Cauchy-Neumann问题
向 妮,吴 燕,窦 楠,张俊玮
(湖北大学数学与统计学学院,湖北武汉 430062)
本文研究了一类抛物型Monge-Ampère型方程的Cauchy-Neumann问题.通过构造辅助函数,利用函数在极大值点的性质及柯西不等式等方法对方程的解进行估计,得到了方程解的全局二阶梯度估计.接着利用抛物方程的一般理论,进一步得到在光滑条件下,解的长时间存在性,推广了抛物型Monge-Ampère方程的结果.
抛物型Monge-Ampère型方程;Cauchy-Neumann问题;先验估计;梯度估计
1 引言
椭圆型Monge-Ampère方程已得到广泛研究,具体可见文献[3–5].在文献[5]中,作者考虑Monge-Ampère型方程半线性Neumann边值问题,通过证明二阶导数的先验估计得到该类方程Neumann边值问题经典解的存在性,唯一性以及正则性.关于完全非线性方程Neumann边值问题也有一些研究成果,如参考文献[9].抛物型Monge-Ampère型方程是一类典型的完全非线性抛物方程,它在最优控制理论等方面的研究中具有重要的应用,许多学者对此类方程进行了深入研究[1,2,7,8,10–12].本文考虑抛物型Monge-Ampère型方程的Cauchy-Neumann问题,形如
其中Ω是Rn中的A-凸区域,n≥2,∂Ω∈C4,Du为梯度向量,D2u为u的Hessian矩阵,是n×n的对称矩阵值函数,是正的向量值函数,ϕ∈C2,1(∂Ω×R)是向量值函数,ν是∂Ω上的单位内法向量.一般用x,z,p分别表示Ω,R,Rn中的元素.
进一步地,当D2u−A(x,u,Du)正定时,称u是椭圆解.为了得到问题(1.1)–(1.3)椭圆解的先验估计,要求A,B,ϕ,u0满足适当的光滑性条件和结构性条件:若函数A满足
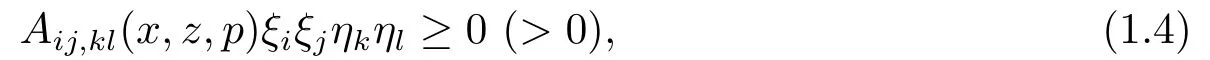
则称A是正则(严格正则)的,其中若函数A满足
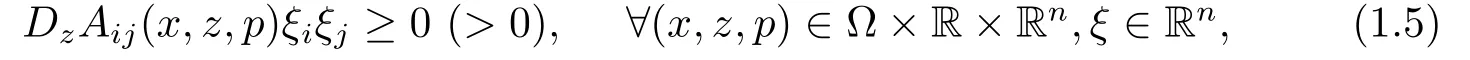
称A对z是非减(严格递增)的.同样地,若函数B和ϕ满足

则称B和ϕ对z是非减(严格递增)的,u0满足相容性条件

另外,区域Ω满足A-凸条件,即存在函数使得在∂Ω上φ=0,Dφ≠0,在 Ω内φ<0且满足不等式

其中I为单位矩阵,δ1为正常数.为了获得问题(1.1)–(1.3)解的C2估计,还需要假设问题(1.1)–(1.3)的有界上解 ¯u存在且满足

下面给出本文的主要结论.
定理1.1设为抛物型Monge-Ampère型方程的Cauchy-Neumann问题(1.1)–(1.3)的椭圆解,Ω∈C4是Rn中A-凸区域,满足(1.4)–(1.5)式,满足(1.6)式,满足(1.7)式,满足(1.8)式.假设问题(1.1)–(1.3)的有界上解存在且满足(1.10)–(1.12)式,则有

其中C是依赖于n,A,B,ϕ,u0,,|u|1,Ω,δ1的常数.
注定理1.1中假设(1.1)–(1.3)式的上解有界,因为定理1.1得到(1.13)式中二阶导数被C控制,而C是依赖于的常数,故如果不假设上解有界,则不能得到解的二阶梯度估计.
为了保证t=0处的光滑性,需要假设u0满足相容性条件

其中m≥0,u,ui,···关于时间的导数可以由(1.1)和(1.3)式得到.
在梯度估计的证明中,还需要A的结构性条件

其中p∈Rn,µ0为正常数.
基于前面的先验估计,结合连续性方法以及抛物方程的一般理论,可以得到问题(1.1)–(1.3)光滑解的存在性和正则性如下.
定理1.2设Ω是Rn中有界光滑的A-凸区域,n≥2,且满足(1.4),(1.5)和(1.15)式,满足(1.6)式,满足(1.7)式,满足相容性条件(1.8)和(1.14)式.假设问题(1.1)–(1.3)的光滑有界上解存在且满足(1.10)–(1.12)式,则对任意的t≥0,问题(1.1)–(1.3)存在光滑解.另外,当t→∞时,u光滑地收敛到光滑函数u∞,其中u∞满足Neumann边值问题
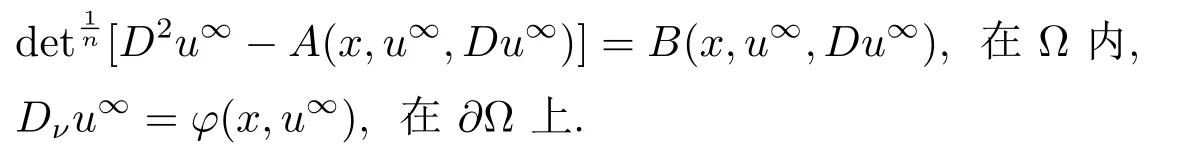
2 预备知识
这一节,先介绍与证明相关的一些基本概念和基本引理,然后给出解的C0和C1估计.定义算子记其中是{wij}的逆矩阵.
引理2.1设且u,v是椭圆解,是n×n对称矩阵值函数满足(1.5)式,是向量值函数满足(1.6)式,假设u,v满足如下条件
(1)在Ω×[0,T)上,

(2)在∂Ω×[0,T]上,如果u>v,那么uν>vν;
证令考虑


其中h∈[0,1],
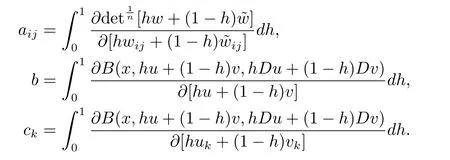
由u(x,t),v(x,t)是椭圆解可知(aij)是正定矩阵,又由(1.5),(1.6)式可得由条件(1),可以得到
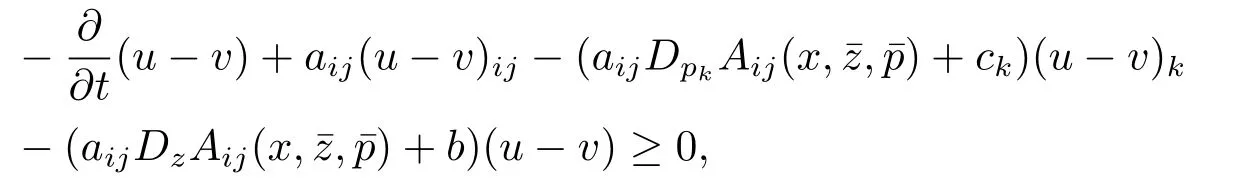
由抛物方程的极值原理得

这里(u−v)+=max{u−v,0}.
接下来,假设u−v在∂Ω×[0,T]上取得正极大值,则u−v>0,且Dν(u−v)≤0,这与条件(2)矛盾,故u−v不能在∂Ω×[0,T]上取得正极大值.再根据条件(3),故有u≤v在上恒成立.
为了证明问题(1.1)–(1.3)解的先验估计,给出以下引理.
引理2.2设Ω是Rn中的A-凸区域,为问题(1.1)–(1.3)的椭圆解,满足(1.5)式,满足(1.6)式,满足(1.7)式.如果对t=0成立,则对任意的t>0,有恒成立.
证对(1.1)式关于t求导可得

由椭圆解知Fij为正定矩阵,由 (1.5),(1.6)式得DzAij≥0,DzB≥0,从而可以得到FijDzAij+DzB≥0,则由抛物方程的极值原理得
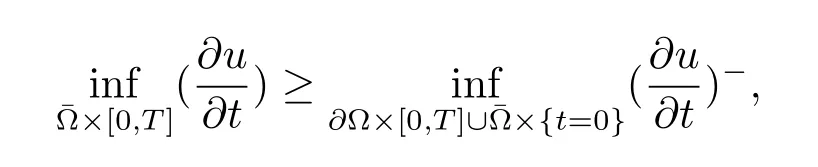


若存在点(x0,t0)∈Ω×(0,T)使得则由抛物方程的强极值原理得这与t=0时矛盾;若存在点使得则与Hopf引理矛盾.
综上可得,对任意的t>0,恒成立.
接下来给出问题(1.1)–(1.3)解的C0和C1估计.
定理2.1设Ω是Rn中有界的A-凸区域,为问题(1.1)–(1.3)的椭圆解,满足(1.5)式,满足(1.6)式,满足(1.7)式,假设问题(1.1)–(1.3)的有界上解存在且满足(1.10)–(1.12)式,则有其中C是依赖于的常数.
证由相容性条件 (1.8)和引理 2.2可得对任意的t>0有则有u(x,t)≥u(x,0)=u0(x),已知问题 (1.1)–(1.3)存在上解根据引理 2.1有从而可以得到其中C是依赖于的常数.
定理2.2设 Ω是 Rn中有界的A-凸区域,为问题 (1.1)–(1.3)的A-凸解,满足 (1.5)式,满足 (1.6)式,满足 (1.7)式.假设问题 (1.1)–(1.3)的有界上解存在且满足(1.10)–(1.12)式.如果对t=0有成立,则有其中C是依赖于的常数.
证首先对关于t求导得


由上面的计算可得
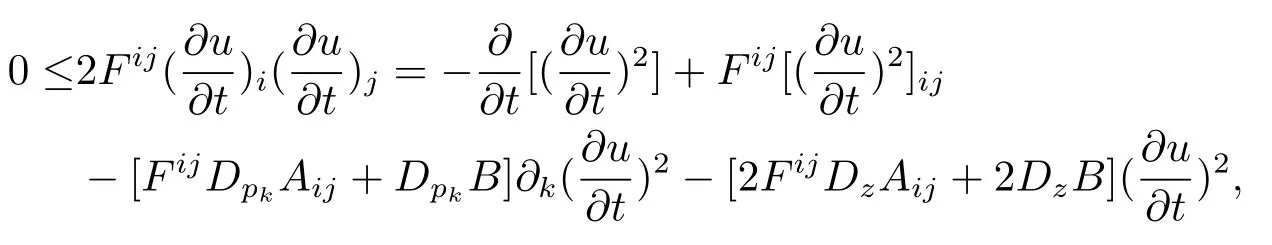
由椭圆解知Fij为正定矩阵,由 (1.5),(1.6)式得DzAij≥0,DzB≥0,从而可以得到2FijDzAij+2DzB≥0,则由抛物方程的极值原理得



由文献[11]中的定理9可得对任意的t0∈[0,T],有

其中M1是依赖于n,A,B,ϕ,Ω的常数.由t0的任意性可得

其中C是依赖于n,A,B,ϕ,Ω,M1的常数.
3 C2估计
本节给出定理1.1的证明,在证明二阶梯度估计之前先介绍一个引理,此引理对证明二阶梯度估计非常重要,其证明过程和文献[6]中的引理2.1类似,省略证明细节.
引理3.1设是问题(1.1)–(1.3)的椭圆解,是问题(1.1)–(1.3)的椭圆有界上解,其中A满足(1.4)–(1.5)式,则有其中N是正常数,ε,C是依赖于的正常数.
首先定义辅助函数v,G如下


定理1.1的证明本定理的证明通过对v在上的最大值的估计,得到对应的D2u在×[0,T]上的估计,从而得到本定理的结论.
证下面分两种情形证明定理1.1.
假设v(x,t)在点(x0,t0)处取得最大值,且以下所有的计算都在点(x0,t0)处进行.
情形一若(x0,t0)∈Ω×(0,T),根据(3.1)式中v和G的定义知,G也在点(x0,t0)处取得最大值.对G关于xi求偏导得
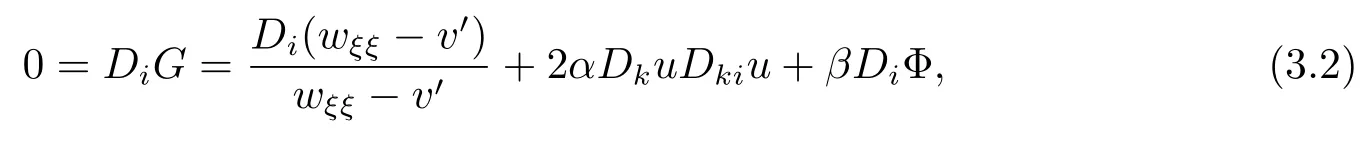
再对DiG关于xj求偏导得

将算子Lt作用到G上得

其中第一个不等式运用了(3.2),(3.3)式和
首先将算子Lt作用到log(wξξ−v′)上得


其中第三个等式运用了算子Lt(wξξ−v′)的定义.
接着将算子Lt作用到|Du|2上得

同理,第三个等式运用了算子Ltuk的定义.将(3.5),(3.6)式代入(3.4)式得

首先估计(3.7)式中的Lt(wξξ−v′),将(1.1)式沿ξ方向求导得

再次对(3.8)式沿ξ方向求导得

接着将算子Lt作用到uξξ上得
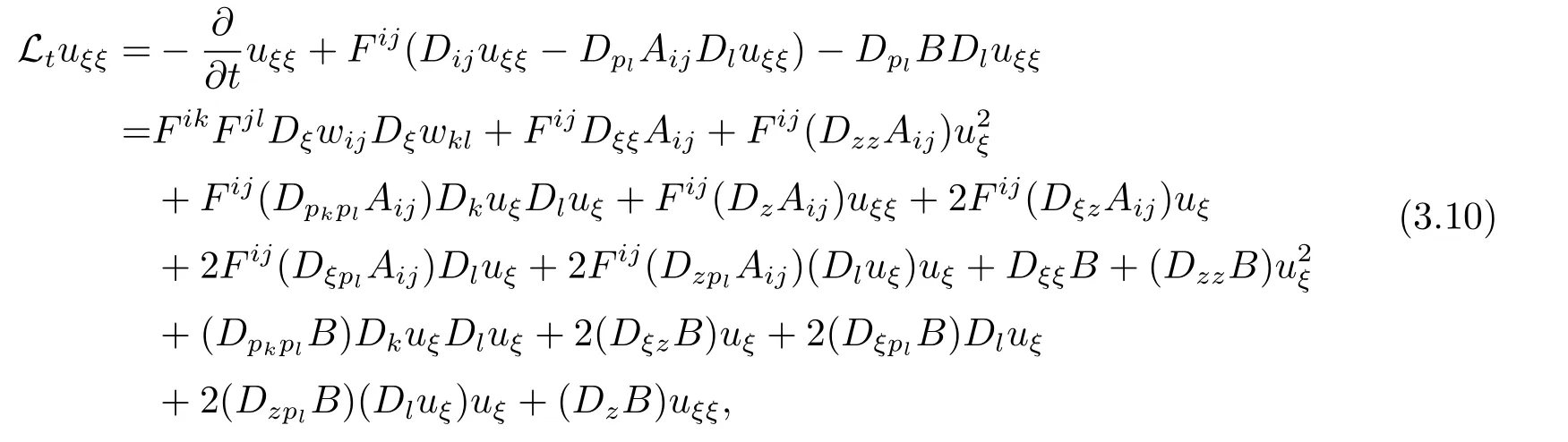
其中第二个等式是将(3.9)式代入所得.由(3.10)和(1.4)式可以得到

其中J=trFii,C是依赖于n,A,B,|u|1,Ω的常数.同理可得

结合(3.11),(3.12),(3.13)式可得

其中C是依赖于n,A,B,|u|1,Ω的常数.

其中θ>0,C(θ)是依赖于θ的正常数.进一步,估计2αDkuLtuk,将算子Lt作用在uk上可得

其中第二个等式是将(1.1)式关于xk求导代入得到的.则由(3.16)和(2.1)式得

其中C是依赖于n,A,B,|u|1,Ω的常数.由引理3.1得

合并(3.14),(3.15),(3.17),(3.18)式得

假设{wij}在(x0,t0)处为对角矩阵函数,有最大特征值w11,且w11>1,否则结论已证.首先估计(3.19)式的三阶导数项.由文献[11]中的(3.48)式可以得到

由于v′是有界的,w11,wξξ是可比较的,则对任意的θ>0,存在更大的常数C(θ),若w11>C(θ),则有

由(3.20),(3.21)式可得

由(3.2)式中的DiG=0可得

由(3.23)式和柯西不等式可得

其中C是依赖于n,a,N,¯u,φ,|u|1,Ω的常数.结合 (3.19),(3.21),(3.22),(3.24)式得对w11>C(θ),有
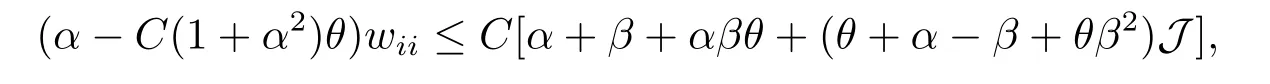
先选择α,β足够大,然后选择θ是充分小的正常数,从而可以得到估计wii(x0,t0)≤C,其中C是依赖于A,B,Ω,|u|1,Ω的常数.从而可以得到|D2u(x,t)|对应的估计.
情形二若(x0,t0)∈∂Ω×[0,T],考虑当ξ属于三种不同的方向,分别来估计v(x0,t0,ξ).
首先将切算子δi作用到(1.2)式上可以得到

其中δi=(δij− τiτj)Dj,可以得到

其中τ为任意的切向量.
(i)ξ是点(x0,t0)处的单位法向量.首先定义辅助函数g如下:g=νkDku−ϕ(x,u).将算子Lt作用到g上得

接下来,将算子Lt作用到u上可得

将(3.16),(3.27)式代入(3.26)式可得
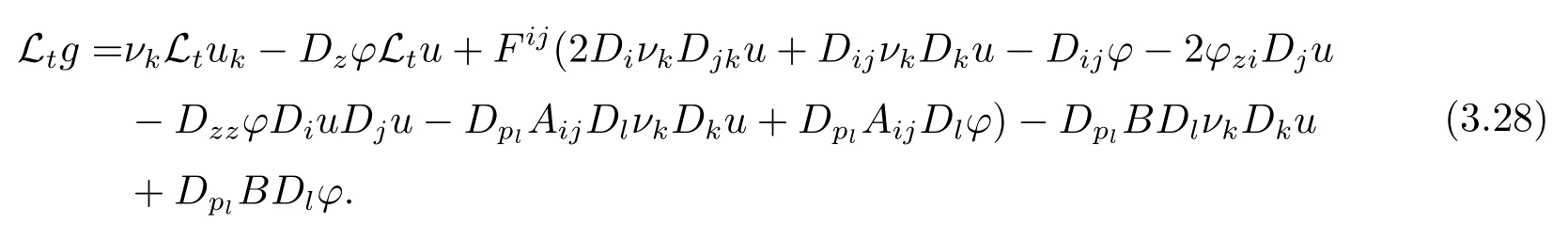
由(3.16),(3.27)和(3.28)式可得|Ltg|≤C(1+J+|D2u|),其中C是依赖于Ω,A,B,ϕ,|u|1,Ω的常数.又因为所以

又由于φ是A-凸区域的定义函数,由(1.9)式可得

结合(3.29),(3.30)式,并选取−φ为闸函数,由Hopf引理的证明可以得到


结合(3.31),(3.32)式可以得到

则由(3.33)式可得

(ii)ξ是点(x0,t0)处的非切非法向量.单位向量ξ可以被写成ξ=(ξ·τ)τ+(ξ·ν)ν,且τ·ν=0,(ξ·τ)2+(ξ·ν)2=1.由v′的定义可得

由v的定义得

其中第二个等式是将(3.35)式代入所得,第四个不等式是由v在点(x0,t0)和向量ξ处取得最大值所得.再结合(3.34),(3.36)式得

(iii)ξ是点(x0,t0)处的切向量,则(ξ·ν)=0,由v′的定义知v′(x0,t0,ξ)=0.假设在点(x0,t0)的法向量为ν=(0,···,0,1),wij(x0,t0)是对角阵,且有最大特征值w11(x0,t0)>1,否则结论已证.计算DνΦ可得


其中第二个不等式利用了v′(x0,t0,ξ)=0,由(3.37)式可得c0=aN,
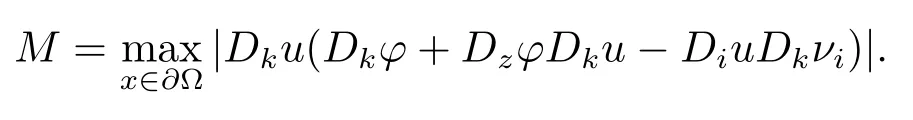
由(3.38)式可得

另外,对(1.2)式沿切向求二阶导得

在点(x0,t0)处对切向量ξ,有
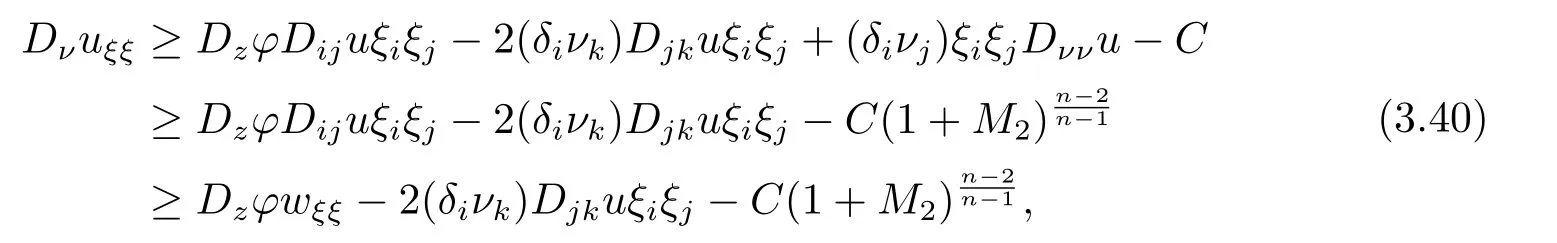
第二个不等式由(3.33)式得到.结合(3.39),(3.40)式可以得到

观察(3.41)式右边的第一项的二阶导数项,由(3.25)式可以得到在点(x0,t0)的估计

取β满足从而可以得到故可以得到其中C是依赖于n,A,a,N,ϕ,|u|1,Ω的常数.
从上面(i),(ii),(iii)三种情况得,若v在边界点 (x0,t0)处取得上的最大值,则v(x0,t0,ξ)在上是有界的,从而Dξξu(x0,ξ)在上是有界的.
[1]保继光,李美生.一般区域上的抛物型Monge-Ampère方程[J].数学杂志,1998,18(3):22–26.
[2]李德生,王志林.二阶完全非线性抛物型方程的周期解[J].数学杂志,1998,18(1):23–28.
[3]Gilbarg D,Trudinger N S.Elliptic partial differential equation of second order[M].Berlin:Springer,2001.
[4]Guan P,Wang X J.On a Monge-Ampère equation arising in geometric optics[J].J.Di ff.Geom.,1998,48(48):205–223.
[5]Jiang F,Trudinger N S,Xiang N.On the Neumann problem for Monge-Ampère type equations[J].Canad.J.Math.,2016,68(6):1334–1361.
[6]Jiang F,Trudinger N S,Yang X P.On the Dirichlet problem for Monge-Ampère type equations[J].Calc.Var.Part.Di ff.Equ.,2014,49:1223–1236.
[7]Kim Y H,Streets J,Warren M.Parabolic optimal transport equations on manifolds[J].Intern.Math.Res.Not.,2010,2012(19):4325–4350.
[8]Kitagawa J.A parabolic flow toward solutions of the optimal transportation problem on domains with boundary[J].J.Für Die Reine Und Angewandte Mathematik,2010,2012(672):127–160.
[9]Lions P L,Trudinger N S,Urbas J I E.The neumann problem for equations of monge-ampère type[J].Commun.Pure Appl.Math.,1986,39(4):539–563.
[10]Schnürer O C,Schwetlick H R.Translating solutions for Gauss curvature flows with Neumann boundary conditions[J].Pac.J.Math.,2004,213:89–109.
[11]Wang J,Liu H,Yang J.The initial and Neumann boundary value problem for a class parabolic Monge-Ampère equation[J].Abs.Appl.Anal.,2013,2013(1):699–704.
[12]Wang G,Wang W.The first boundary value problem for general parabolic Monge-Ampere equation[J].J.P.D.E.,1990,2:1–15.
THE CAUCHY-NEUMANN PROBLEM FOR PARABOLIC TYPE AND MONGE-AMPÈRE TYPE EQUATIONS
XIANG Ni,WU Yan,DOU Nan,ZHANG Jun-wei
(School of Mathematics and Statistics,Hubei University,Wuhan 430062,China)
In this paper,we study the Cauchy-Neumann problem for parabolic type and Monge-Ampère type equations.By establishing an anxiliary function,using the methods of the properity at the maximum point and cauchy inequality,we prove the global gradient estimates for second order derivatives.And by using the general theory of parabolic equations,we obtain that such solution exists for all times under smoothness and regularity conditions,which generalizes the results of parabolic type and Monge-Ampère type equations.
parabolic type and Monge-Ampère type equation;Cauchy-Neumann problem;a priori estimate;gradient estimate
35K20;35K61
O175.29
A
0255-7797(2017)06-1261-14
2017-01-13接收日期:2017-04-25
湖北省教育厅科学技术研究计划重点项目(D20171004).
向妮(1981–),女,重庆云阳,副教授,主要研究方向:偏微分方程.
