超弹性形状记忆合金阻尼器的减振特性研究

张振华，绳 飘, 王钦亭，吴志强

(1.河南理工大学 力学系，河南 焦作 454000；2.天津大学 力学系，天津 300072)

超弹性形状记忆合金阻尼器的减振特性研究

张振华1，绳 飘1, 王钦亭1，吴志强2

(1.河南理工大学 力学系，河南 焦作 454000；2.天津大学 力学系，天津 300072)

研究了环境变量(温度和外激励幅值)对超弹性形状记忆合金阻尼器减振特性的影响。用多线性本构模型来表示SMA伪弹性，建立了SMA振动系统的动力学模型。通过平均法求解了方程主共振的幅频响应解，并用数值方法验证其计算的准确性。通过定义SMA振动系统与对应线性系统的共振幅值比、共振频率比来表示SMA阻尼器的减振和调频效果，并研究了环境变量与其的定量关系。研究结果表明：温度升高对SMA减振和调频是不利的；而外激励幅值在一定的范围内取值时，SMA阻尼器具有良好的减振和调频效果。此研究结果可为SMA阻尼器使用环境条件的选择提供参考。

形状记忆合金;伪弹性;温度;减振

形状记忆合金(Shape Memory Alloy，SMA)的伪弹性是SMA在奥氏体相下由应力诱发马氏体相变的一种物理和力学行为。伪弹性SMA能够在卸载后自主回复变形，其最大可回复应变能达到8%，并且会产生应力-应变的滞后关系，能够起到大变形回复和阻尼的作用。此外SMA具有较好的抗疲劳和抗腐蚀能力，能够适应不同的工程环境。正因为伪弹性SMA这些优秀的品质，其被作为阻尼和自定心元件广泛地应用于工程结构的振动控制。

Graesser等[1]开始研究伪弹性SMA在结构振动控制的应用。此后，学者们利用SMA构造各种减、隔振装置来对框架建筑[3-6]、桥梁[7-8]和机械结构[9]等进行振动控制研究，结果均表明SMA作为阻尼和自定心元件能够有效降低结构动力学响应。

温度与SMA的相变和阻尼特征密切相关，因此有必要研究温度等参数对SMA阻尼器的结构振动控制效果的影响。而目前利用SMA伪弹性进行被动减隔振的研究中，考虑温度影响的研究还比较少。Huang等试验研究了在温度11 °C～120 °C范围内SMA振子动力学响应特征，研究结果表明温度增加使SMA的阻尼作用降低。Ozbulut等[10-11]用神经模糊数学的方法建立了考虑温度SMA伪弹性模型，进而用数值方法研究了温度对NiTi-SMA-摩擦支座减振作用的影响，研究表明在温度为0 °C、20 °C和40 °C时，该隔振器均能起到有效地降低结构地震反应，但是隔振效率随温度增高而降低。上述试验和数值研究的结果是离散，温度对SMA阻尼器减振效果的具体规律需要进一步的理论分析。

本研究采用分段线性模型描述SMA的伪弹性，利用平均法求解SMA振子的幅频响应方程，并通过定义SMA振子与其派生线性系统的共振峰值比和频率比来定量研究温度和外激励对SMA减振特性的影响规律，为SMA阻尼器适用温度和激励环境的选择提供依据。

1 SMA双线性本构模型

SMA的Tanaka-Liang-Brinson(TLB)系列模型[12-14]是目前应用的最为广泛的系列模型之一。TLB系列本构模型形式简单，而且避开自由能等参数测量的困难，因此被广泛应用在含SMA结构的分析中。但是该类模型中的非线性相变热力学方程给求解问题带来了困难。随着研究的深入和工程应用的需要，有学者在TLB系列模型的基础上提出了分段线性化伪弹性本构模型[15-16]，该类模型避开了非线性热力学方程求解的困难，极大地提高了非线性的效率，线性显式本构关系在数值计算中不受计算子步大小的影响，能够很好的收敛，因此越来受到人们的重视，对SMA阻尼器的动力学研究及工程设计有比较重要的意义。

本文采用文献[16]中的分段线性模型来表示SMA的伪弹性，其应力-应变关系如图1所示。

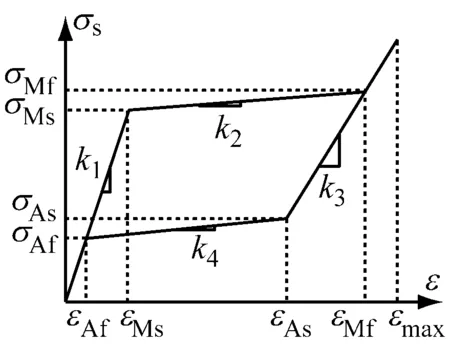
(a) εmax>εMf

(b) εMs<εmax≤εMf图1 SMA多线性模型Fig.1 The SMA multilinear model

图1(a)表示SMA的卸载发生在相变完成后的应力-应变曲线，而图1(b) SMA的卸载发生在相变过程中的应力-应变曲线。

SMA的应力-应变关系可用式(1)表示

σs=kiε+σi0, (i=1,2,3,4)

(1)

式中：k1=EA;k2=(σMf-σMs)/(εMf-εMs);k3=

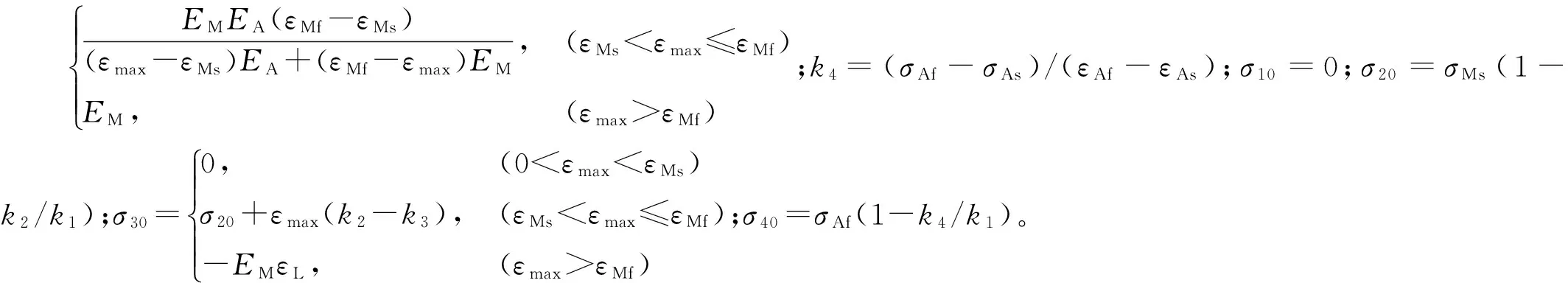
根据文献[16]，式(1)中的相变应力、应变和温度之间存在如式(2)所示的关系

σMs=CM(T-Ms)，εMs=σMs/EA，

σMf=CM(T-Mf)，εMf=εL+σMf/EM，

σAs=CA(T-As)，εAs=εL+σAs/EM，

σAf=CA(T-Af)，εAf=σAf/EA

(2)

式中：Ms和Mf分别为SMA马氏体相变开始和结束温度；As和Af分别为SMA奥氏体相变开始和结束温度；CA和CM为SMA相变材料常数；T为SMA的温度。本文中SMA的参数如表1所示。

表1 SMA参数列表Tab.1 List of parameters of SMA

滞洄阻尼是SMA的特征之一，图2是当εmax=εMf时，伪弹性SMA的等效阻尼比随温度的变化规律。结果表明当温度从0 ℃增加到50 ℃时，SMA等效阻尼比减少了75%，说明温度的升高会显著减弱SMA的阻尼能力。

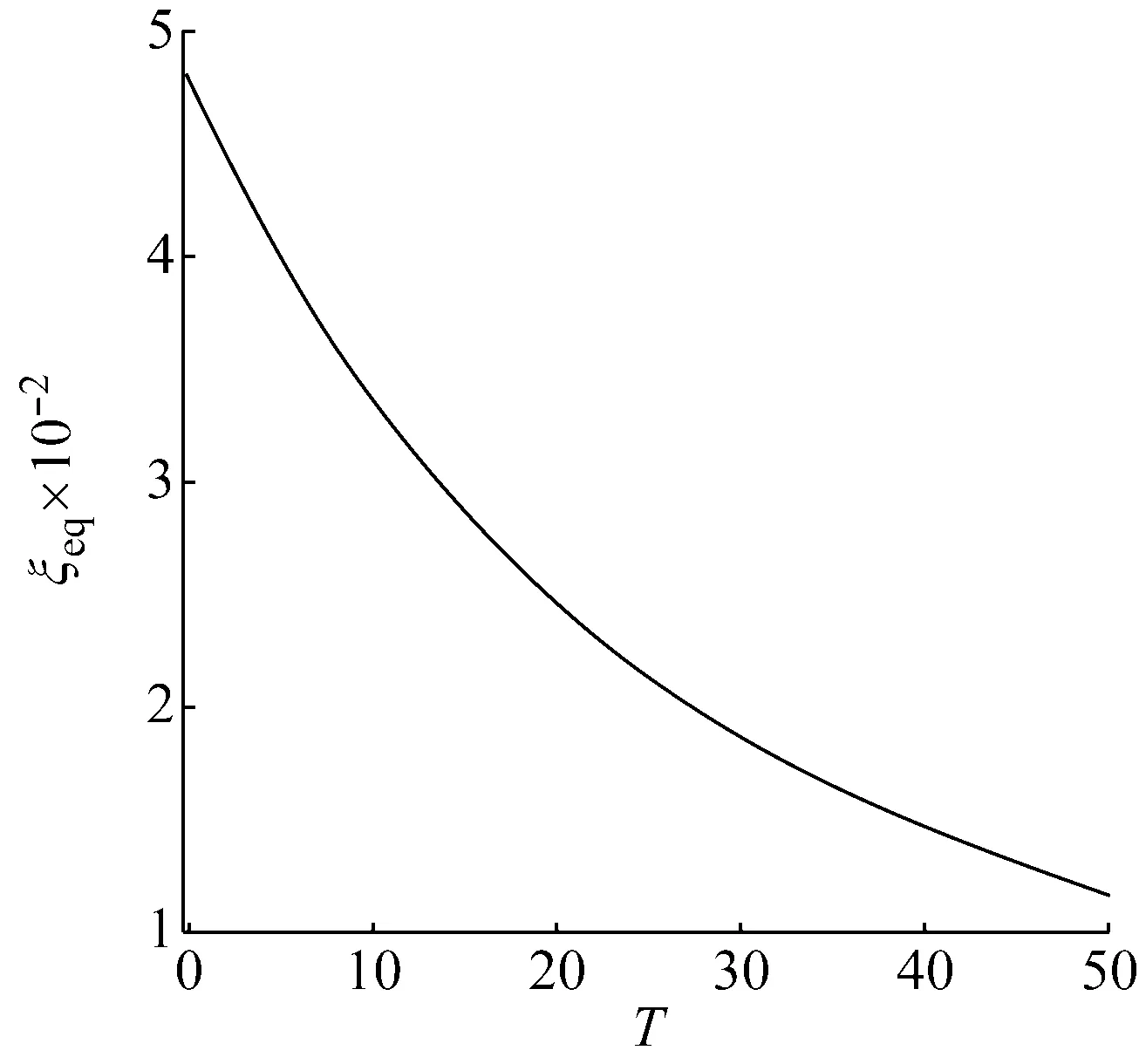
图2 SMA的等效阻尼比与温度关系Fig.2 Relationship between equivalent damping ratio of SMA and temperature

2 动力学方程及求解

2.1动力学方程

SMA振动系统如图3所示，其中F(X)是形状记忆合金引起的回复力，因为在本研究中SMA是丝材，不承受压力，所以F(X)具体表达式为

(3)

式中,A为SMA的横截面积，且取SMA和弹簧的原长度为L。

图3 动力系统Fig.3 The dynamic system

容易建立该系统的动力学模型如式(4)

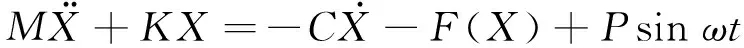
(4)

式中，M,K,C分别为振动系统中的质量、刚度、结构阻尼系数。

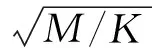
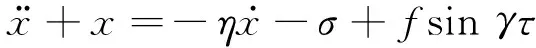
(5)

从ξ定义可知，ξ越大表明SMA提供的回复力在系统中所占比例越大，在本文中取ξ=2×10-6，此时SMA元件奥氏体弹性阶段刚度是线性弹簧元件的1/10。此外取阻尼系数η=0.01。

2.2平均法求解

平均法是摄动法的一种，可以被用来求解弱非线性动力学方程。下面用平均法求解动力学方程式(5)，并用数值计算对求解结果进行验证。

设系统主共振响应解为

x=ycos(γt+θ)

(6)

式中:y为振幅;θ为相角;两者均是时间的缓变函数。令φ=γt+θ，用平均法对式(5)求解可得

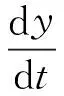
(7a)

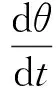
(7b)

其中,

对By，Bθ实际计算时，根据伪弹性SMA不同加卸载变形阶段，将积分区间进行划分，积分的具体结果见附录。

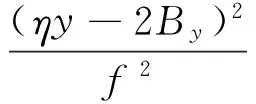
(8)

因为By和Bθ是y的分段函数，因此所得到的幅频响应方程也是分段的。如果给出所有的参数，就可以根据式(8)画出系统的幅频响应图。如图4所示，是本系统典型的幅频响应曲线，图中上下两条点划线分别表示y=εMs和y=εMf，此两条线将幅频响应曲线分成三段，自下而上分别为第一段、第二段和第三段。此三段分别对应着形状记忆合金的奥氏体下的线性段、马氏体相变段和相变完成段，第一段为线性段，第二段呈现软特性，第三段呈现硬特性。图中的圆点是数值计算的结果，和平均法计算的结果非常接近，证明本文中平均法得到的幅频方程是准确的。

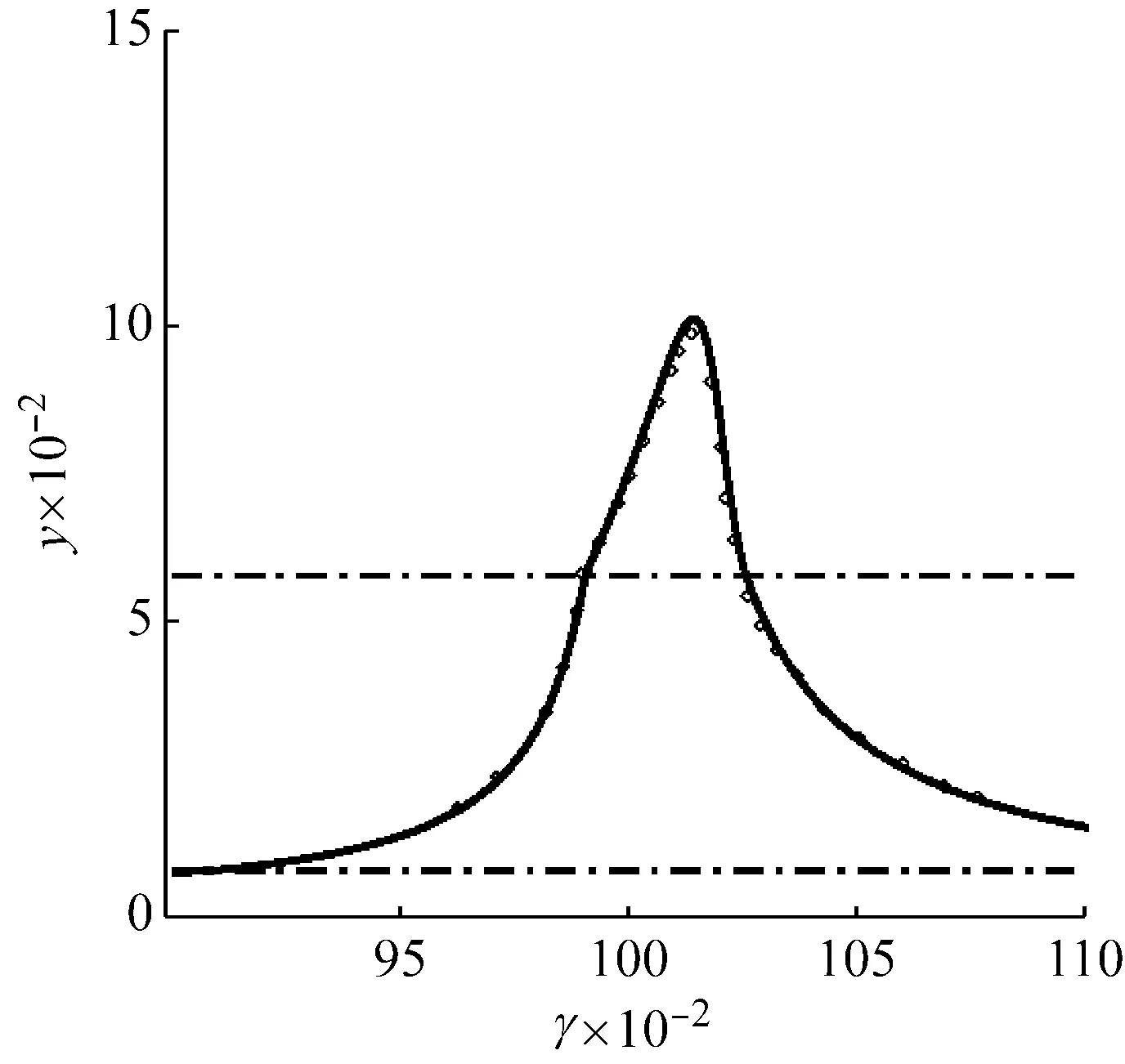
图4 典型的幅频响应曲线和数值结果的比较Fig.4 The classical amplitude-frequency response curves and their numerical results

3 幅频响应分析

3.1温度和外激励幅值对幅频响应特性的影响

为了更直观的了解温度和外激力幅值对幅频响应特征的影响，图5和图6分别给出了不同外激励幅值和不同温度下的幅频响应曲线。图5表明，外激励幅值较低时，系统呈现明显的软特性，随着外激励幅值增大，系统的软特性减弱，当幅频响应极值超过马氏体相变结束应变后，系统由软特性向硬特性过渡；在图6中给出了2个特定外激励幅值下不同环境温度中的幅频响应曲线。在图6(a)的曲线验证了环境温度对曲线软特性的影响，同时也表明，当幅频响应的峰值处在第二段时，幅频响应的峰值随着环境温度增加而增加；从图6(b)幅频响应的峰值达到第三段，温度对其极值仍有一定影响；从图6(a)和图6(b)上总体上看，温度和外激励对幅频响应曲线的峰值和滞后性质有着一定的影响，为了更加明确温度和外激励幅值对系统减振和调频的作用，将在4.2中通过定义SMA系统和对应线性系统的幅频响应共振峰值比和共振频率比，找出温度和外激励幅值对SMA减振性能的具体影响规律。

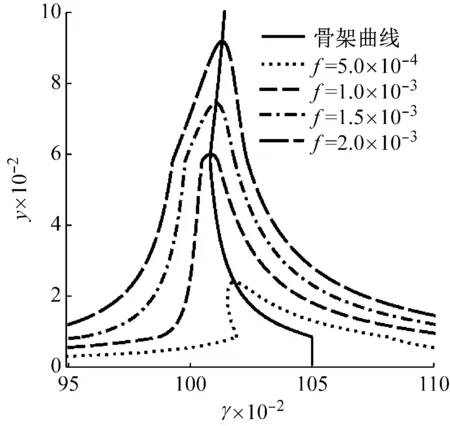
图5 外激励幅值对幅频响应性质的影响(T=0 °C)Fig.5 Influence of external excitation amplitude on characteristics of amplitude-frequency responses (T=0 °C)

3.2减振与调频效果分析

在SMA马氏体相变开始前，系统处于线性阶段，此时SMA没有滞后效应；当SMA马氏体相变开始后(y>εMs)，SMA的滞后效应才起作用。本节就讨论振动幅值y>εMs时，SMA对系统的减振和调频作用。

幅频响应式(8)对γ求导，得幅频响应的极值点(γm,ym)应满足的条件为

γm=1+Bθ(ym)

(9a)

f2=[ηym-2By(ym)]2

(9b)

式(9a)为幅频响应的骨架曲线，和激励幅值无关。

将式(5)中由SMA产生的回复力σ用SMA奥氏体状态下的弹性阶段的本构方程代替，得到线性化的动力系统如下

(10)

(11)

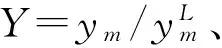
(a) f=1×10-3

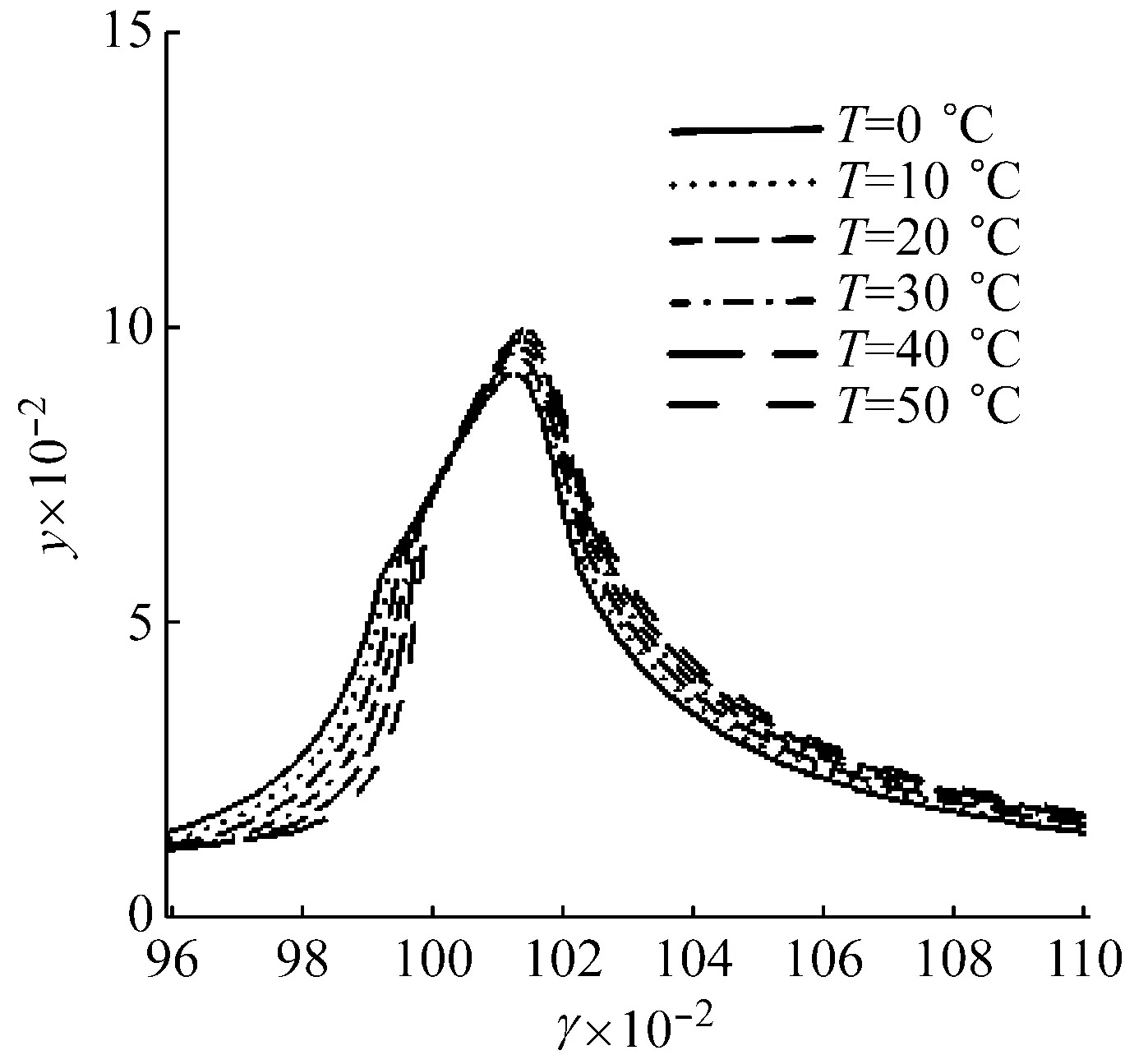
(b) f=2×10-3图6 温度对幅频响应性质的影响Fig.6 The influence of temperature on characteristics of the amplitude-frequency response curves

(12a)

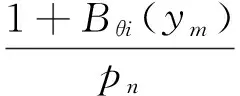
(12b)

根据式(12)可以做峰值比Y和频率比Γ随外激励幅值的变化曲线，如图7所示，该图给出不同温度下外激励频率对峰值比和频率比的影响。

从图7中可以清楚看出，在同一条曲线上存在着一个非光滑点，此非光滑点是由于式(12)的分段性质造成的。在非光滑点之前，SMA的振动幅值未能达到马氏体相变结束时的应变εMf；非光滑点以后，SMA振动幅值已经超过εMf。总体上来看，外激励的幅值和SMA的温度对峰值比和频率比都有较为明显的影响。共振峰值比和共振频率均随外激励幅值的增加先减小后增大，但共振峰值比在SMA马氏体相变完成前达到了极小值(0.46-0.65)，而共振频率比是在SMA马氏体相变完成时取得极小值。随着温度的增加，共振峰值比和频率比均有不同程度的增加，当温度从0 ℃增加到50 ℃时，共振峰值比的极小值增加了39%，而共振频率比的极小值增加了0.3%。故温度对SMA的减振作用影响显著，这是因为SMA的阻尼效应随温度增加而减弱。而Huang等通过SMA振子的自由振动试验表明了SMA的阻尼减振作用会随温度升高而减弱，温度从11 °C 增加至80 °C时，SMA的阻尼比减少85%。

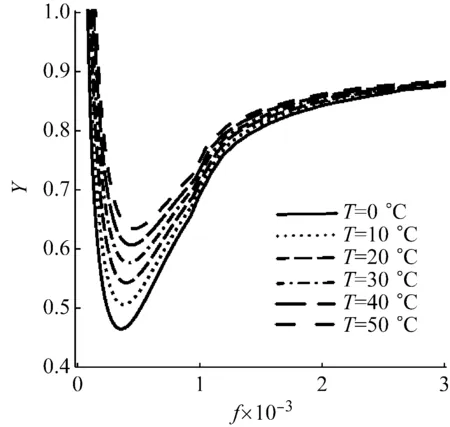
(a) 共振峰值比

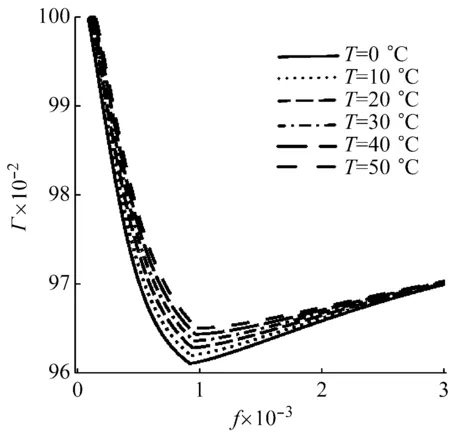
(b) 共振频率比图7 SMA的减振和调频作用Fig.7 The damping and frequency tuning effects of SMA

4 结 论

研究了含SMA阻尼器振动系统的动力学响应和温度、外激励幅值之间的关系。具体研究结果如下：

(1) 温度对SMA的阻尼性能有比较大的影响，当SMA的最大应变取马氏相变结束应变时，SMA的等效阻尼比在温度从0 ℃增加到50 ℃时减小75%。

(2) 随外激励幅值增加，SMA的减振效果先增加后降低，且在SMA应变极值处于马氏体相变中段时其减振效果最好，此时含SMA系统的共振峰值可低至其派生线性系统的46%；随温度的增加SMA的减振作用显著减弱，当温度从0 ℃增加到50 ℃时，含SMA系统与其线性派生系统共振峰值比的极小值增加39%。

(3) 根据本研究中的定量式(12)，可确定使SMA阻尼器具有理想减振效果的温度和外激励幅值，为SMA阻尼器的工程应用提供指导。

[1] GRAESSER E J, COZZARELLI F A. Shape memory alloys as new materials for aseismic isolation [J]. Journal of Engineering Mechanics, 1991, 117(11): 2590-2608.

[2] 薛素铎，石光磊，庄鹏. SMA复合摩擦阻尼器性能的试验研究[J]. 地震工程及工程振动，2007，27(2)：145-151.

XUE Suduo，SHI Guanglei，ZHUANG Peng. Performance testing of SMA incorporated friction dampers [J]. Earthquake Engineering and Engineering Vibration, 2007,27(2): 145-151.

[3] 刘海卿，崔衍斌，欧进萍，等. SMA复合支座一巨型框架结构体系减震效果分析[J]. 地震工程与工程振动, 2008, 28(6): 239-244.

LIU Haiqing，CUI Yanbin，OU Jinping，et al. Damping effect analysis of mega-frame structure based on SMA compound bearing[J]. Earthquake Engineering and Engineering Vibration, 2008, 28(6): 239-244.

[4] QIAN H, LI H, SONG G. Experimental investigations of building structure with a superelastic shape memory alloy friction damper subject to seismic loads [J]. Smart Materials and Structures, 2016, 25(12): 125026.

[5] CHOU C C, TSAI W J, CHUNG P T. Development and validation tests of a dual-core self-centering sandwiched buckling-restrained brace (SC-SBRB) for seismic resistance [J]. Engineering Structures, 2016, 121(8): 30-41.

[6] SHINOZUKA M, CHAUDHURI S R, MISHRA S K. Shape memory alloy supplemented lead rubber bearing (SMA-LRB) for seismic isolation [J]. Probabilistic Engineering Mechanics, 2015, 41(6): 34-45.

[7] KHODAVERDIAN A, GHORBANI-TANHA A K, RAHIMIAN M. An innovative base isolation system with Ni-Ti alloy and its application in seismic vibration control of Izadkhast bridge [J]. Journal of Intelligent Material Systems and Structures,2012, 23(8): 897-908.

[8] DEZFULI F H, ALAM M S. Seismic vulnerability assessment of a steel-girder highway bridge equipped with different SMA wire-based smart elastomeric isolators [J]. Smart Materials and Structures, 2016, 25(7): 075039.

[9] HUANG H, CHANG W S, MOSALAM K M. Feasibility of shape memory alloy in a tuneable mass damper to reduce excessive in service vibration [J]. Structural Control and Health Monitoring, 2016,24(2):1-14.

[10] OZBULUT O E, MIR C, MORONI M O, et al. A fuzzy model of superelastic shape memory alloys for vibration control in civil engineering applications [J]. Smart Materials & Structures, 2007, 16(3):818-829.

[11] OZBULUT O E, HURLEBAUS S. Evaluation of the performance of a sliding-type base isolation system with a NiTi shape memory alloy device considering temperature effects [J]. Engineering Structures, 2010, 32(1): 238-249.

[12] TANAKA K, NAGAKI S. A thermomechanical description of materials with internal variables in the process of phase transitions [J]. Ingenieur-Archiv, 1982, 51(5): 287-299.

[13] LIANG C, ROGERS C A. A multi-dimensional constitutive model for shape memory alloys [J]. Journal of Engineering Mathematics, 1992, 26(3): 429-443.

[14] BRINSON L C, HUANG M S. Simplifications and comparisons of shape memory alloy constitutive models [J]. Journal of Intelligent Material Systems and Structures, 1996, 7(1): 108-114.

[15] 陈鑫，李爱群，左晓宝. 超弹性形状记忆合金简化多维本构模型[J]. 东南大学学报(自然科学版), 2009, 39(4): 813-818.

CHEN Xin, LI Aiqun, ZUO Xiaobao. Simplified multidimensional constitutive model of superelasticity shape memory alloy [J]. Journal of Southeast University (Natural Science), 2009, 39(4): 813-818.

[16] MOTAHARI S A, GHASSEMIEH M. Multilinear one-dimensional shape memory material model for use in structural engineering applications [J]. Engineering Structures, 2007, 29(6): 904-913.

附录：

在式(7)中By1，By2，By3，Bθ1，Bθ2，Bθ3的表达式为

By1=0

2σ30(ε1-y)-2σ20(y-εMs)]

2σ30(εAs-εMf)-2σ20(εMf-εMs)]

Bθ1=ξk1/2

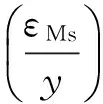
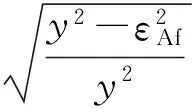
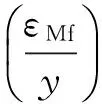
Vibrationreductioncharacteristicsofasuperelasticshapememoryalloydamper

ZHANG Zhenhua1, SHENG Piao1, WANG Qinting1, WU Zhiqiang2

(1. Department of Mechanics, Henan Polytechnic University, Jiaozuo 454000, China;2. Department of Mechanics, Tianjin University, Tianjin 300072, China)

In order to choose the reasonable application environment of a shape memory alloy (SMA) damper, the influences of environment parameters such as temperature and amplitude of excitation on the vibration reduction characteristics of the shape memory alloy damper were investigated. The dynamic equation of a vibration system was established where a bilinear model was adopted for the damper to describe the superealsticity of SMA, and then the equation was transformed into the dimensionless one. Subsequently, the primary resonance amplitude-frequency response of the dynamic system was acquired by the average method, and its accuracy was confirmed by the numerical method. Finally, the concepts of resonance amplitude ratio and resonance frequency ratio between the system with SMA damper and the corresponding linearized system were defined to express respectively the effects of vibration reduction and frequency tuning of the SMA damper, and the relationships between the environment parameters and the effects were studied. The results indicate that the vibration reduction effect will be weakened as the temperature increases, and the SMA damper will work well in a certain range of excitation amplitude. The results give a guide to choose the application environment for the SMA damper.

shape memory alloy; superelasticity; temperature; vibration reduction

TU352.1+2; TB123

A

10.13465/j.cnki.jvs.2017.19.026

国家自然科学基金资助项目(51308195)；河南省科技厅科技攻关项目(132102210252)

2016-10-17 修改稿收到日期：2016-12-26

张振华 男，博士,副教授，1981年5月生