基于自适应概率主成分分析的滚动轴承故障特征增强方法

胡爱军，南 冰

(华北电力大学 能源动力与机械工程学院，河北 保定 071003)

基于自适应概率主成分分析的滚动轴承故障特征增强方法

胡爱军，南 冰

(华北电力大学 能源动力与机械工程学院，河北 保定 071003)

针对实际工程中滚动轴承微弱故障信号特征难以提取的问题，提出了一种新的自适应概率主成分分析(Adaptive Probabilistic Principal Component Analysis, APPCA)的轴承故障特征增强方法。概率主成分分析(Probabilistic Principal Component Analysis, PPCA) 能够提取信号的主要故障特征，去除背景噪声干扰，但结果易受到主成分数与原始变量维数选择的影响。为了自适应实现最佳分析结果，利用粒子群算法多参数寻优特性，根据最大峭度准则确定影响PPCA的最佳影响参数组合。原信号通过APPCA方法处理后，背景噪声得到有效抑制，故障特征得到增强，最后通过包络分析识别故障特征。仿真和实验结果证明了该方法的有效性。

滚动轴承；概率主成分分析；故障诊断

滚动轴承出现早期局部故障时，由于故障产生的冲击成分通常比较微弱，并淹没于强烈的背景噪声中，导致难以提取到轴承故障特征频率信息[1]。近些年，针对此类问题，不少学者进行了深入研究。唐贵基等[2]提出先对故障信号做最大相关峭度解卷积预处理增强信号冲击特征，然后计算解卷积信号的包络信号，最后对包络信号做1.5维谱分析，通过分析谱图中幅值突出的频率成分准确判断了故障类型。文献[3]首先利用小波包去除信号中的噪声，后进行LMD分解，选取有效PF集进行功率谱分析，成功提取出了故障特征。文献[4]提出了基于倒谱编辑预白化和形态学自互补Top-Hat变化的方法，先对信号预白化，后对白化信号形态学滤波消除背景噪声的干扰，准确的提取了轴承故障特征频率。文献[5]将EEMD与1.5维能量谱结合，对轴承内圈故障信号分析取得了较为理想的效果。文献[6]将EEMD、度量因子和快速峭度图相结合，较好的提取了轴承故障特征频率。上述方法在轴承故障诊断中均取得了一定的效果，但是这些方法均存在一定的局限性，由于缺少对原始数据的恰当的概率模型，导致一些高频的噪声不能够被正确的分离，同时某些故障特征信息可能被当作噪声去除[7-8]。

概率主成分分析(Probabilistic Principal Component Analysis, PPCA)，是一种信号分析方法，其首先建立一个恰当的概率模型，然后基于这个模型重新生成一个新的样本数据，最后信号主成分可以通过正交投影的方法获得。PPCA的本质是将方差最大的方向作为主要特征，并且在各个正交方向上将数据“离相关”，也就是让它们在不同正交方向上没有相关性。因此PPCA不仅可以去除噪声，还能增强对原始信号特征信息的保留，现已应用于特征提取与模态识别等领域[9]。文献[10]通过多次实验对比分析的方法，针对特定的故障信号选择最优的主成分数k与原始变量维数n，较好的提取出了轴承故障频率的边频带。但由于其算法不具有自适应性，针对不同的故障信号时，最优参数取值需要重新进行对比分析，因此在实际轴承故障诊断中受到了一定程度的限制。

鉴于上述问题，本文提出了一种自适应的概率主成分分析方法。为了自适应实现最佳分析结果，利用粒子群多参数寻优特性，根据最大峭度准则确定影响PPCA的最佳影响参数组合，并应用于滚动轴承的故障特征增强。通过仿真和实验结果，证明了该方法能有效的增强轴承故障特征，适合用于轴承故障诊断。

1 PPCA基本原理和方法

PPCA作为一种信号分析方法，通过先将原始数据投影到其他的坐标空间，后投影的方式来提取信号的主特征分量。其本质是将方差最大的方向作为主要特征，并且在各个正交方向上将数据“离相关”，因此PPCA不仅可以去除噪声，还能增强对原始信号特征信息的保留。

1.1PPCA模型

PPCA模型首先假设n维原始变量数据X满足如下模型关系[11-12]

X=P·u+E

(1)

X～(0,PPT+σ2I)

(2)

其中u的先验分布为

(3)

且原始数据X在隐变量u条件下的先验概率分布为

(4)

根据式(3)和式(4)可得原始数据X的概率分布为

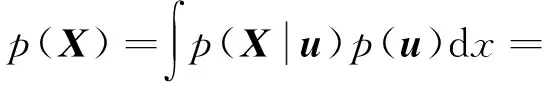
(5)

式中，C=PPT+σ2I为两参数P与σ2决定的协方差矩阵。为了得到上述模型的P和σ2采用EM算法进行估计，推导出其迭代公式

P=SP(σ2I+M-1PTSP)-1

(6)

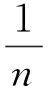
(7)

式中：S为原始数据的协方差矩阵;M=PTP+σ2I；两参数P与σ2可由式(6)和式(7)多次迭代至收敛求得，P与σ2计算出来后即可建立PPCA模型。

1.2PPCA降维

当PPCA模型被建立后，可以用以下变换求取降维后的数据。

(8)

由式(8)可知，各主成分数据(降维后的数据)是原始变量数据X在相应主成分向量pi的投影。PPCA去噪效果由主成分数k与原始变量维数n确定，当其中任何一个参数设置不合适，都难以达到理想的分析效果。现阶段，参数主要是根据人为经验选取，缺乏自适应性，因此在实际轴承故障诊断中受到了一定程度的限制。

2 APPCA方法原理与实现过程

粒子群算法[13]具有良好的全局寻优能力，本文采用粒子群算法对PPCA算法的两个参数进行优化，可实现主成分数k与原始变量维数n的自适应选取。假设D维空间中，种群X=(X1,X1,…,XM)包含M个粒子组成，其中第i个粒子表示一个D维向量Xi=(xi1,xi2,…,xiD)，代表第i个粒子在D维搜索空间中的位置。第i个粒子的速度为Vi=(vi1,vi2,…,viD)，Qi=(qi1,qi2,…,qiD)为个体局部均值，G=(g1,g2,…,gD)为种群全局极值，各粒子通过Pi和G迭代更新自身速度和位置，公式为

(9)

式中:ω为惯性权重；d=1,2,…,D；i=1,2,…,M；α为当前迭代次数；c1和c2为加速度因子；η为介于[0,1]的随机数。

粒子群算法寻优时，需要确定一个适应度函数，粒子每次更新位置时需计算当前位置对应的函数值，通过对比进行更新。信号中冲击成分的比重影响着峭度指标的大小，信号所包含的冲击成分越多，峭度值越大，因此本文将PPCA处理后信号的峭度值K作为适应度函数，表达式为

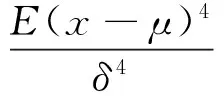
(10)

式中:x为振动信号;μ为信号x的均值;δ为信号x的标准差。

利用粒子群参数寻优的具体步骤如下：

步骤1初始化粒子群算法的各项参数。

步骤2初始化粒子种群，以影响参数组合[k,n]作为粒子的位置，随机初始化各粒子的位置与移动速度。

步骤3计算每个粒子的位置对应的适应度值。

步骤4对比适应度值大小并更新个体局部极值和种群全局极值。

步骤5更新粒子的位置和速度。

步骤6循环迭代，转置步骤3,直至迭代次数达到最大设定值，输出最佳适应度值及粒子的位置。

在设置粒子群寻优参数时，参考了文献[14-15]中的参数取值，如表1所示。

表1 粒子群算法各项参数Tab.1 Each parameter of particle swarm algorithm

自适应概率主成分分析故障特征增强方法实现过程如图1所示。利用粒子群多参数寻优特性，根据最大峭度准则确定影响PPCA的最佳影响参数组合，可有效避免参数设定时人为主观因素带来的弊端。原信号通过APPCA方法处理后，背景噪声得到有效抑制，故障特征得到增强，最后通过包络分析识别故障特征。

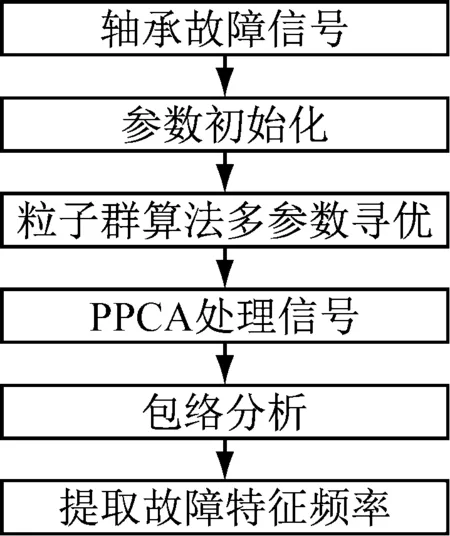
图1 APPCA方法流程图Fig.1 Flow chart of APPCA method

3 仿真分析及应用

3.1仿真信号分析

采用文献[16]中的滚动轴承内圈故障模型进行模拟。故障数学模型如式(11)所示

(11)

式中，τi为第i次冲击相对于平均周期T的微小波动；Ai为以1/fr为周期的幅值调制；h(t)为指数衰减脉冲；B为系统的衰减系数；A0=2，CA=0；fr=20 Hz为轴承所在工作轴的转频；fi=150 Hz为内圈故障通过频率；fn=3 kHz为系统固有频率；n(t)为信噪比-12 db的高斯白噪声。设置采样频率为fs=12 800 Hz，取4 096点数据分析。加噪故障仿真信号的时域波形如图2所示，图3为直接对加噪轴承内圈故障仿真信号做包络谱的分析结果。图3包络谱中没有找到幅值突出的频率成分，说明仅包络分析难以提取到强背景噪声下的轴承微弱故障信号。

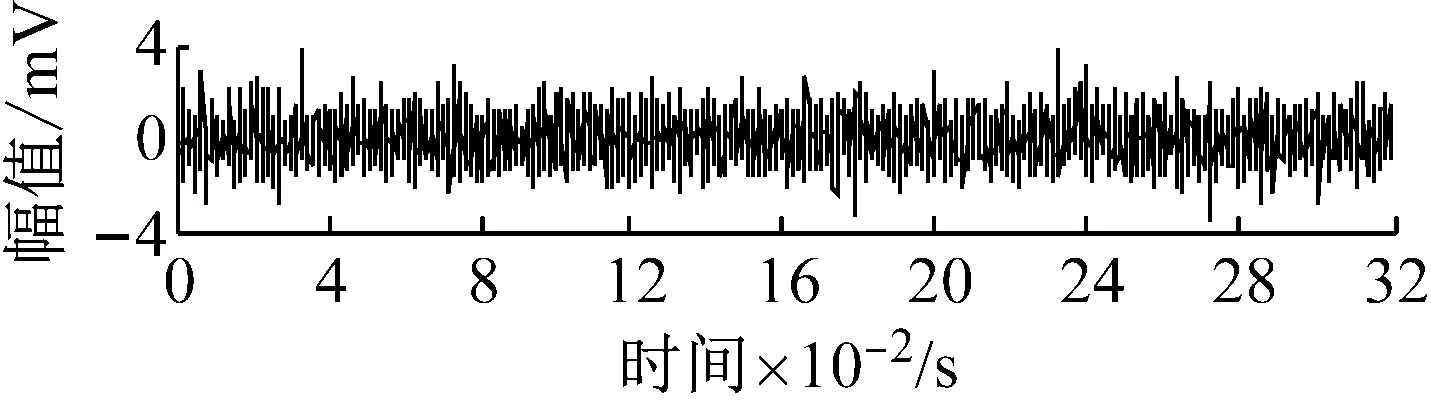
图2 加噪内圈故障仿真信号时域波形Fig.2 Time domain waveform of inner ring fault simulation signal with noise

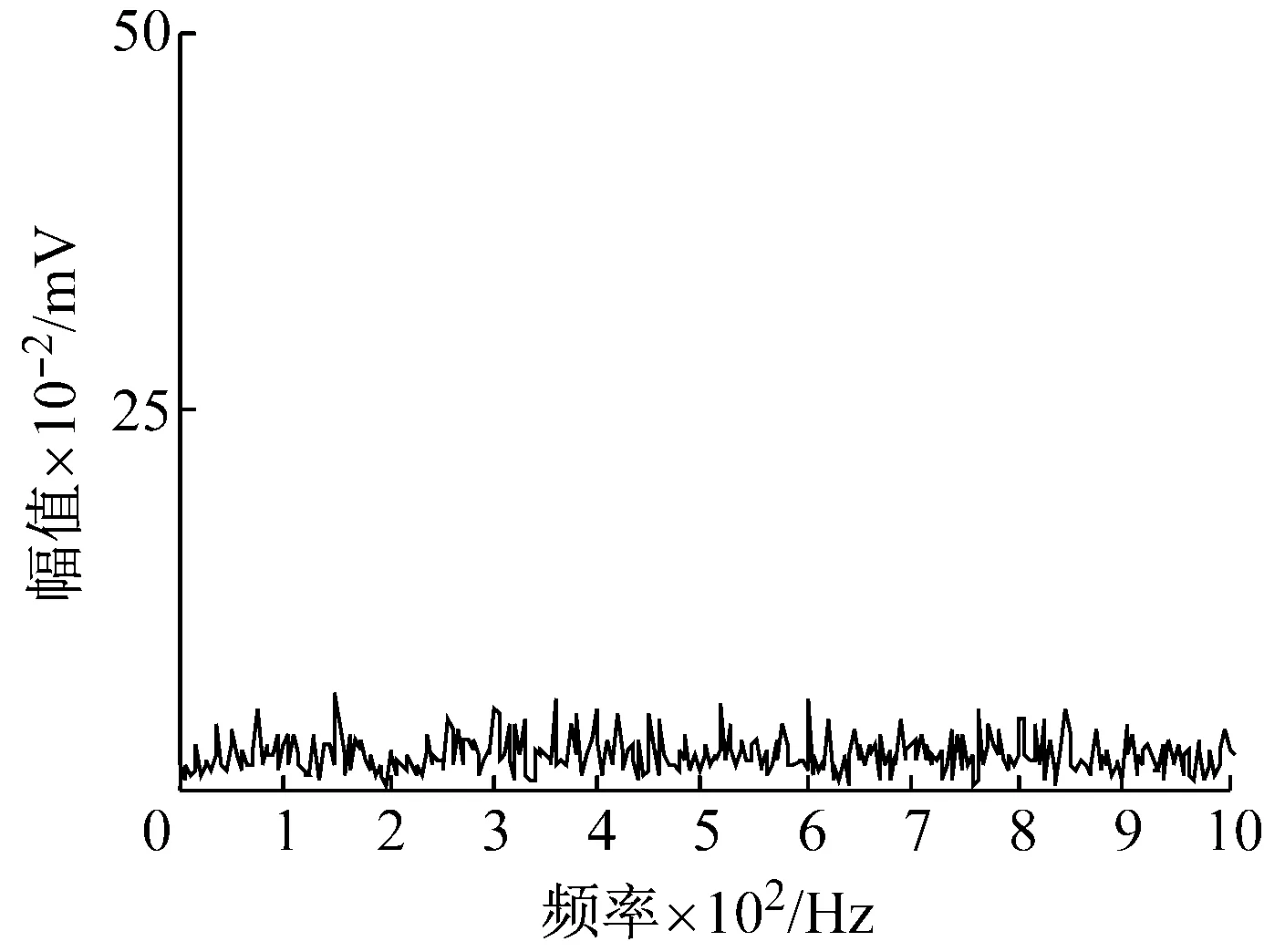
图3 内圈故障仿真信号包络谱Fig.3 The envelope spectrum of the inner ring fault simulation signal

利用APPCA方法对故障信号进行分析，首先将所选4 096点轴承故障数据xr去均值得到一维数据x，将x构造n维原始变量数据X如式(12)所示

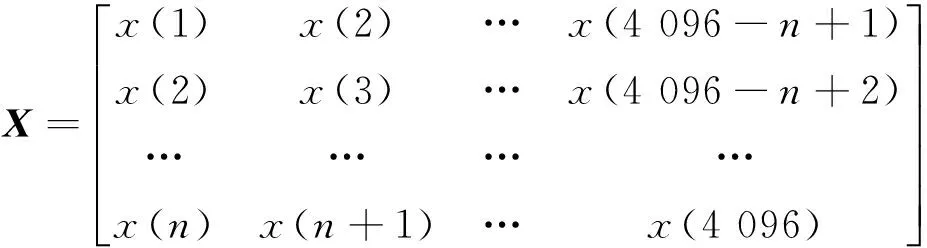
(12)

其次将参数P与σ2值初始化后按照式(6)式(7)经过多次迭代求解参数值，当两参数取值确定后，按照式(1)建立PPCA模型。在模型中n与k的取值直接影响到主成分提取的效果，根据参考文献[10]的取值，当固定参数k的取值为2，参数n的取值大于20时，轴承故障信号的信噪比会降低，不利于轴承故障特征的增强，因此本文参数n的最大取值设置为20。另外由于PPCA算法的本质是优先将方差最大的方向作为主要特征，轴承故障信息主要集中在特征值较大的主成分中，背景噪声主要分布在特征值较小的主成分中，k的取值较大时，特征值较小的噪声成分会增加，同时计算负担也会加重，所以参数k的最大值不宜过大。采用粒子群算法对主成分数k与原始变量维数n进行自适应选取，图4为峭度值随进化代数变化的关系曲线，峭度最大值3.65出现在了第11代进化种群中，此时主成分数k=2，原始变量维数n=13。

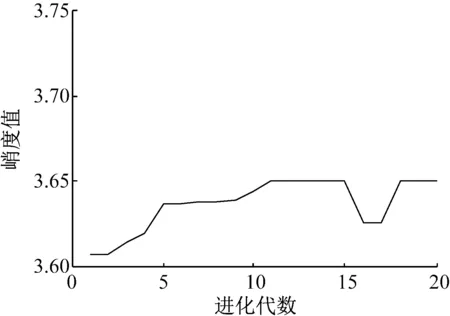
图4 峭度值随进化代数变化的关系曲线Fig.4 Relation curve of kurtosis changing with evolutional generation

PPCA模型建立后，按照式(8)求解出主成分矩阵 (即降维后的数据)，最后将主成分矩阵重构轴承故障仿真信号时域波形如图5所示。图6为轴承故障仿真信号的包络谱。

图5 PPCA处理后仿真信号时域波形Fig.5 Time domain waveform of the simulation signal using PPCA

图6 APPCA方法所得信号包络谱Fig.6 The envelope spectrum of the signal by APPCA method

图6包络谱中可以较为清楚的找到150 Hz、300 Hz频率成分，分别对应轴承故障特征频率及其二倍频，故障特征频率三、四倍频谱线峰值也十分突出。说明APPCA算法处理信号能够去除大量背景噪声，增强轴承的故障特征，效果较理想。

为验证所述方法的优势，与故障诊断领域常用的快速峭度图方法结果作对比。图7为故障信号快速峭度图分析结果，可以看出轴承故障信号最大谱峭度处所对应的分解层数为7，滤波器中心频率和带宽组合为[6 300,200]，即带通滤波器的范围为[6 200,6 400]，在此范围内信号的峭度值与信噪比均达到最大，按照上述的中心频率和带宽构造滤波器对信号进行滤波，所得包络谱如图8所示。通过对比分析发现：快速峭度图滤波后包络谱仅能勉强提取到轴承故障特征频率(150 Hz)，倍频成分均被背景噪声淹没且由于存在较多的干扰谱线(28.1 Hz、65.6 Hz)，无法判断出是内圈故障，与图6相比，故障特征频率幅值水平也存在较大差距。由此表明，APPCA方法在轴承故障特征增强方面具有一定的优势。

图7 内圈故障仿真信号快速峭度图Fig.7 Fast kurtogram of the inner ring fault simulation signal

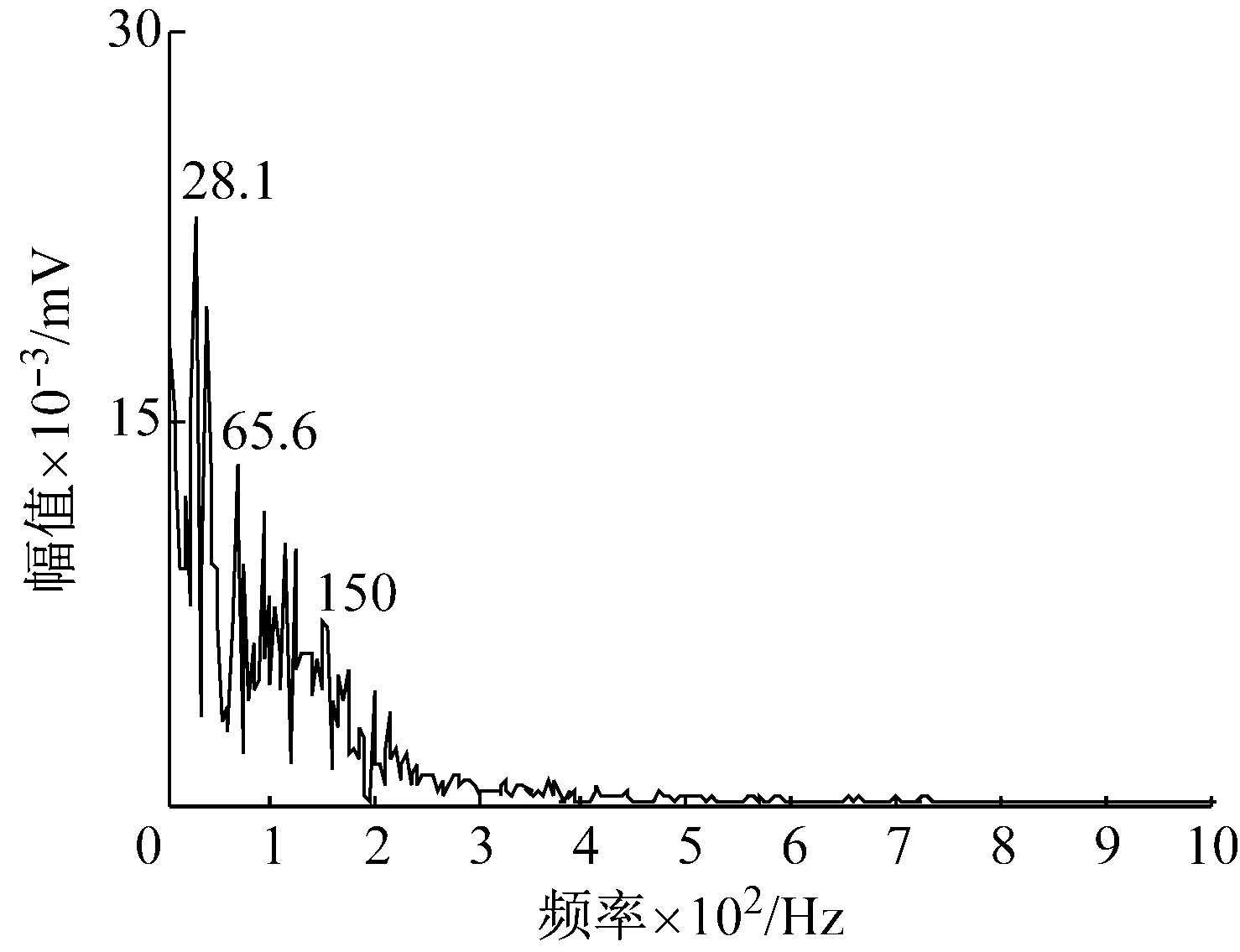
图8 快速峭度图滤波后信号包络谱Fig.8 The envelope spectrum of the signal using fast kurtogram filter

3.2实验信号分析

为了进一步验证该方法对实际轴承故障信号的处理效果，采用美国Case Western Reserve大学的滚动轴承实验数据，轴承型号JEMSKF6023-2RS。故障源是滚动体表面通过电火花加工的直径分别为0.177 8 mm(0.007inch)、0.355 6 mm(0.014inch)、0.533 4 mm(0.021inch)的凹坑。采样频率12 kHz，轴的转速为1 772 r/min。表2为轴承的各个故障特征频率。

选用最轻微的滚动体0.007inch故障数据进行分析，分析点数取8 192点，图9为轴承故障信号的时域波形。直接对轴承信号做包络分析，结果如图10所示。包络谱中存在较多的干扰谱线，仅能提取到接近轴承转频的频率成分(30.0 Hz)，115.7 Hz与滚动体故障频率118 Hz相差较大，且无法找到故障频率的倍频成分。因此对于此轻微故障，仅包络分析效果欠佳。

表2 滚动轴承故障特征频率Tab.2 Fault feature frequency of rolling bearing

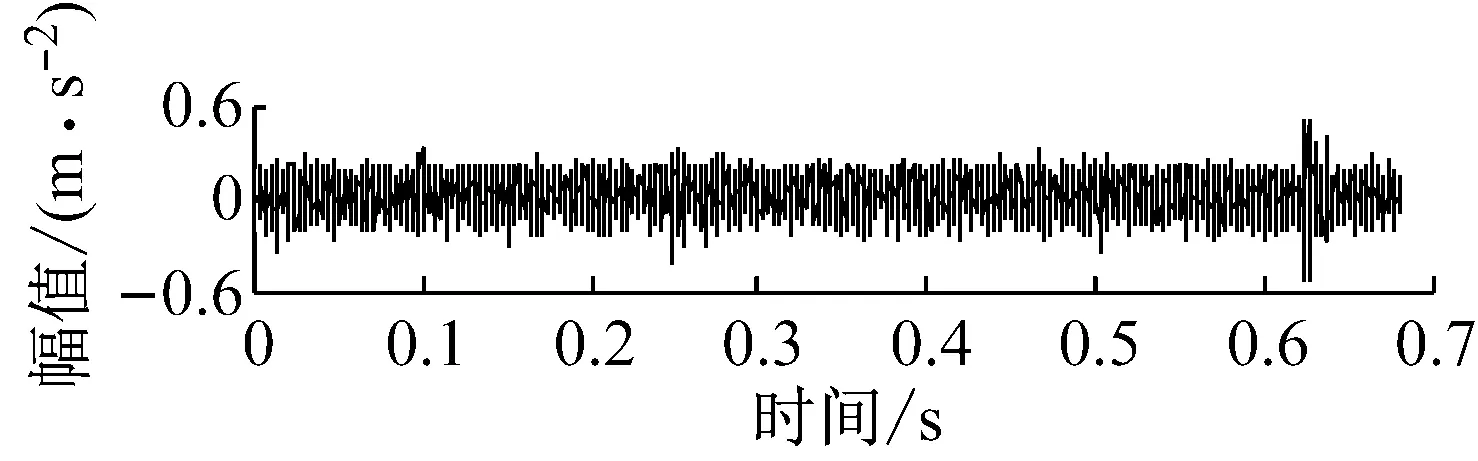
图9 轴承故障信号时域波形Fig.9 Time domain waveform of the bearing fault signal

图10 轴承故障信号包络谱Fig.10 The envelope spectrum of the bearing fault signal

利用APPCA方法对故障信号进行分析。图11为峭度值随进化代数变化的关系曲线，峭度最大值3.812出现在了第10代进化种群中，此时PPCA算法中主成分数k=2，原始变量维数n=20。利用参数优化后的PPCA算法对故障信号处理所得包络谱如图12所示。

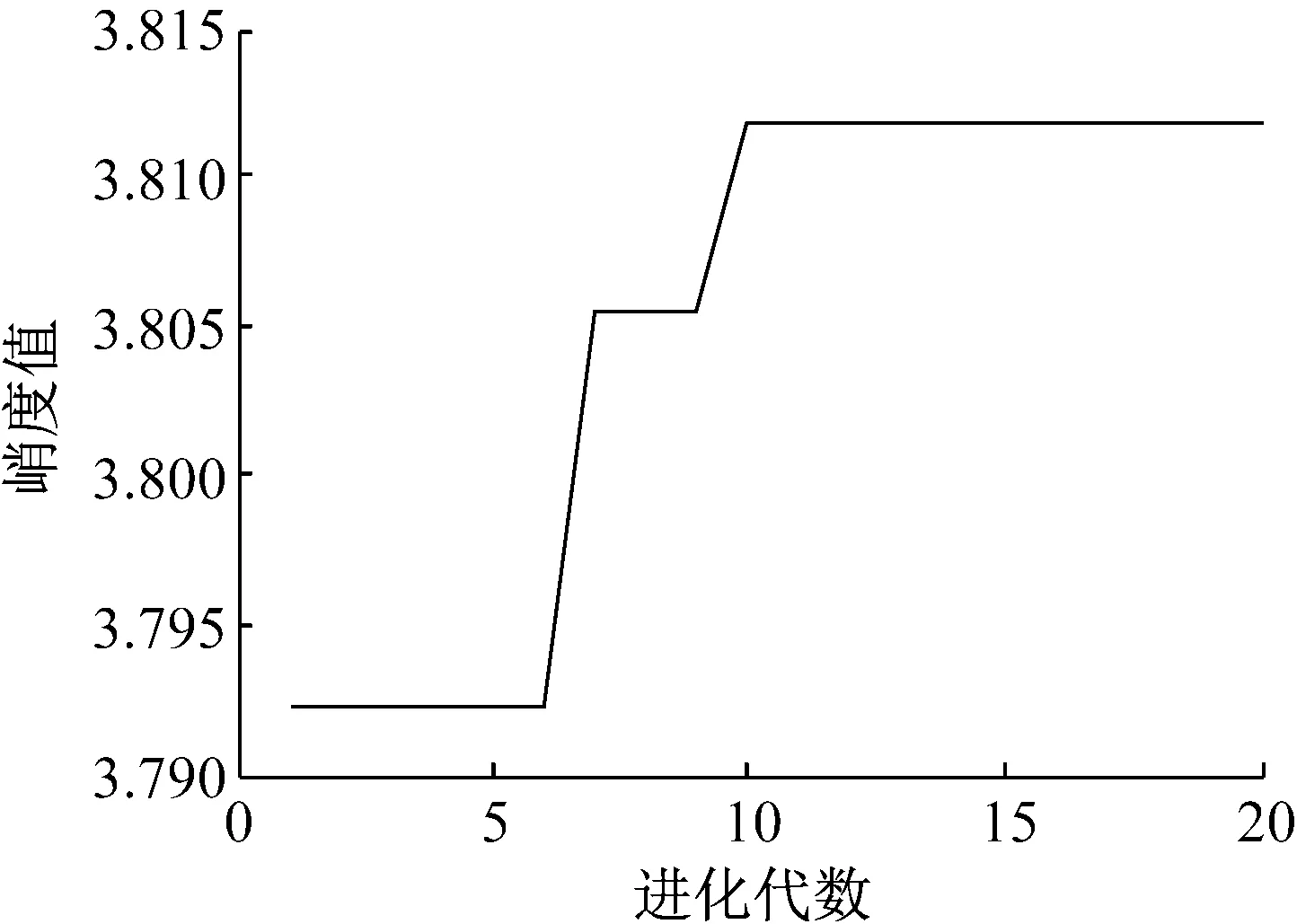
图11 峭度值随进化代数变化的关系曲线Fig.11 Relation curve of kurtosis changing with evolutional generation

图12包络谱中可以较为清楚的找到29.3 Hz、58.6 Hz、117.2 Hz、234.4 Hz等频率成分。其中29.3 Hz、58.6 Hz分别对应轴承转频及其倍频。117.2 Hz、234.4 Hz与滚动体故障特征频率、二倍频成分非常接近，因此可以判断实际情况是轴承滚动体存在故障。

图12 本文方法所得信号包络谱Fig.12 The envelope spectrum of the signal by the proposed method

同样，将所述方法与快速峭度图方法结果作对比，图13为故障信号快速峭度图分析结果。可以看出轴承故障信号最大谱峭度处所对应的分解层数为7，滤波器中心频率和带宽组合为[2 343.75,187.5]，即带通滤波器的范围为[2 250,2 437.5]，在此范围内信号的峭度值与信噪比均达到最大，按照上述的中心频率和带宽构造滤波器对信号进行滤波，所得包络谱如图14所示。

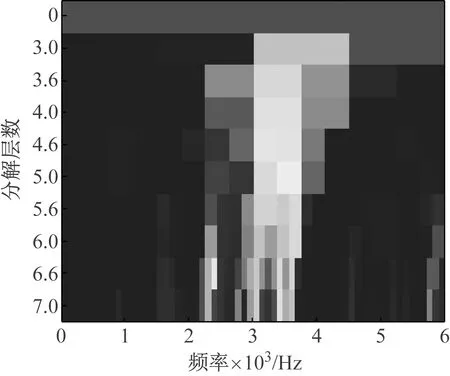
图13 轴承故障信号快速峭度图Fig.13 Fast kurtogram of the bearing fault signal

图14 快速峭度图滤波后信号包络谱Fig.14 The envelope spectrum of the signal using fast kurtogram filter

由图14可以看出包络谱中存在较多的干扰谱线(8.8 Hz、90.8 Hz、114.3 Hz)，而轴承转频及其倍频、滚动体故障特征频率及其倍频被淹没在了背景噪声中，无法确定轴承存在滚动体故障。而APPCA处理后的包络谱图相对干净，基本不存在其他干扰成分，转频及其倍频处谱线峰值十分突出，同时也较易提取到轴承的轻微故障特征。滚动体轻微故障特征信号对比分析结果再次验证了本文所述方法在轴承故障特征增强方面的优势。

4 结 论

实际工程中滚动轴承微弱故障信号易受到背景噪声的干扰，导致仅包络分析难以提取出轴承故障特征。PPCA能够提取信号主要故障特征成分，去除背景噪声干扰，但其算法中主成分数k与原始变量维数n选择起着十分关键的作用。利用粒子群多参数寻优特性，根据最大峭度准则确定影响PPCA的最佳影响参数组合的方法是有效的，可以用于轴承故障特征增强。仿真和实验对比结果证明了该方法的有效性。

[1] 胡爱军, 马万里, 唐贵基. 基于集成经验模态分解和峭度准则的滚动轴承故障特征提取方法[J]. 中国电机工程学报, 2012, 32(11):106-111.

HU Aijun, MA Wanli, TANG Guiji. Rolling bearing fault feature extraction method based on ensemble empirical mode decomposition and kurtosis criterion[J]. Proceedings of the CSEE, 2012, 32(11):106-111.

[2] 唐贵基, 王晓龙. 最大相关峭度解卷积结合1.5维谱的滚动轴承早期故障特征提取方法[J]. 振动与冲击, 2015,34(12):79-84.

TANG Guiji, WANG Xiaolong. Feature extraction for rolling bearing incipient fault based on maximum correlated kurtosis deconvolution and 1.5 dimension spectrum[J]. Journal of Vibration and Shock, 2015,34(12):79-84.

[3] 孙伟, 熊邦书, 黄建萍,等. 小波包降噪与LMD相结合的滚动轴承故障诊断方法[J]. 振动与冲击, 2012, 31(18):153-156.

SUN Wei, XIONG Bangshu, HUANG Jianping, et al. Fault diagnosis of a rolling bearing using Wavelet packet de-noising and LMD[J]. Journal of Vibration and Shock, 2012, 31(18):153-156.

[4] 邓飞跃, 唐贵基, 何玉灵. 基于倒谱预白化和形态学自互补Top-Hat 变换的滚动轴承故障特征提取[J]. 振动与冲击, 2015,34(15):77-81.

DENG Feiyue, TANG Guiji, HE Yuling. Fault feature extraction for rolling element bearings based on cepstrum pre-whitening and morphology self-complementary top-hat transformation[J]. Journal of Vibration and Shock, 2015,34(15):77-81.

[5] 唐贵基, 王晓龙. 基于EEMD降噪和1.5维能量谱的滚动轴承故障诊断研究[J]. 振动与冲击, 2014,33(1):6-10.

TANG Guiji, WANG Xiaolong. Fault diagnosis for roller bearings based on EEMD de-noising and 1.5 dimensional energy spectrum[J]. Journal of Vibration and Shock, 2014,33(1):6-10.

[6] 彭畅, 柏林, 谢小亮. 基于EEMD、度量因子和快速峭度图的滚动轴承故障诊断方法[J]. 振动与冲击, 2012,31(20):143-146.

PENG Chang, BO Lin, XIE Xiaoliang. Fault diagnosis method of rolling element bearings based on EEMD, measure-factor and fast kurtogram[J]. Journal of Vibration and Shock, 2012,31(20):143-146.

[7] TIPPING M E, BISHOP C M. Probabilistic principal component analysis[J]. Journal of the Royal Statistical Society, 1999, 61(3):611-622.

[8] BISHOP C M, TIPPING M E. A hierarchical latent variable model for data visualization[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1998, 20(3):281-293.

[9] 陆超, 陈捷, 洪荣晶. 采用概率主成分分析的回转支承寿命状态识别[J]. 西安交通大学学报, 2015, 49(10):90-96.

LU Chao, CHEN Jie, HONG Rongjing. Recognition of life state for slewing bearings using probabilistic principal component analysis[J]. Journal of Xi’an Jiaotong University, 2015, 49(10):90-96.

[10] XIANG J, ZHONG Y, GAO H. Rolling element bearing fault detection using PPCA and spectral kurtosis[J]. Measurement, 2015, 75:180-191.

[11] BELLAS A, BOUVEYRON C, COTTRELL M, et al. Model-based clustering of high-dimensional data streams with online mixture of probabilistic PCA[J]. Advances in Data Analysis & Classification, 2013, 7(3):281-300.

[12] ZUCCOLOTTO P. Principal component analysis with interval imputed missing values[J]. Asta Advances in Statistical Analysis, 2012, 96(1):1-23.

[13] KENNEDY J, EBERHART R. Particle swarm optimization[C]∥Proceeding of IEEE International Conference on Neural Networks. Perth: IEEE, 1995:1942-1948.

[14] 沈伋, 韩丽川, 沈益斌. 基于粒子群算法的飞机总体参数优化[J]. 航空学报, 2008, 29(6):1538-1541.

SHEN Ji, HAN Lichuan, SHEN Yibin. Optimization of airplane primary parameters based on particle swarm algorithm[J]. Acta Aeronautica ET Astronautica Sinica, 2008, 29(6):1538-1541.

[15] 唐贵基, 王晓龙. 最大相关峭度解卷积结合稀疏编码收缩的齿轮微弱故障特征提取[J]. 振动工程学报, 2015, 28(3):478-486.

TANG Guiji, WANG Xiaolong. Weak feature extraction of gear fault based on maximum correlated kurtosis deconvolution and sparse code shrinkage[J]. Journal of Vibration Engineering, 2015, 28(3):478-486.

[16] 王宏超, 陈进, 董广明. 基于最小熵解卷积与稀疏分解的滚动轴承微弱故障特征提取[J]. 机械工程学报, 2013, 49(1):88-94.

WANG Hongchao, CHEN Jin, DONG Guangming. Fault diagnosis method for rolling bearing’s weak fault based on minimum entropy deconvolution and sparse decomposition[J]. Journal of Mechanical Engineering, 2013, 49(1):88-94.

Faultfeatureenhancementmethodforrollingbearingbasedonadaptiveprobabilisticprincipalcomponentanalysis

HU Aijun, NAN Bing

(School of Energy, Power and Mechanical Engineering, North China Electric Power University, Baoding 071003, China)

Aiming at the difficulty in extracting the features of weak fault signals of rolling element bearings in practical engineering, a new method named adaptive probabilistic principal component analysis (APPCA) was proposed to enhance the features of bearing faults. The method of PPCA is able to extract main fault features and remove background noise interferences, but is easily affected by the number of principal components and the dimension of original variables. In order to adaptively achieve the best analysis result, the particle swarm optimization algorithm with multi-parameter optimization characteristics was applied to search for the optimal combination of influencing parameters of PPCA based on the maximum kurtosis criterion. After the original signal was processed by the APPCA method, the background noise was effectively suppressed, and the fault features were enhanced. Finally, the signal envelope spectrum was analyzed to identify fault features. The simulation and experiment results show the effectiveness of the method.

rolling bearing; probabilistic principal component analysis; fault diagnosis

TH133.3；TH17

A

10.13465/j.cnki.jvs.2017.19.022

国家自然科学基金资助项目(51475164)

2016-06-23 修改稿收到日期：2016-08-20

胡爱军 男，博士，副教授，1971年生