基于正交检验法的颤振分析模态跟踪技术

蒋令闻，杭晓晨，费庆国

(1. 江苏省工程力学分析重点实验室，南京 210096; 2. 东南大学 工程力学系，南京 210096)

基于正交检验法的颤振分析模态跟踪技术

蒋令闻1,2，杭晓晨1,2，费庆国1,2

(1. 江苏省工程力学分析重点实验室，南京 210096; 2. 东南大学 工程力学系，南京 210096)

模态跟踪是颤振分析的关键问题之一。常见的基于模态置信度的跟踪方法在颤振点附近常会出现错误导致跟踪失败。通过探究该方法的数学机理，阐明了基于模态置信度跟踪方法存在的缺陷，进而引入左特征向量，研究了一种基于正交检验法的模态跟踪技术。采用一悬臂直翼盒模型开展仿真研究，在状态空间下进行颤振分析，基于正交检验法得到其根轨迹图，并将模态跟踪结果与MAC值法进行对比，证明了正交检验法具有更好的模态跟踪效果。

颤振；状态空间；特征向量；模态跟踪；模态置信度

颤振是飞行器在飞行中受到来流激励后产生的一种灾难性的破坏振荡，需要通过理论分析和设计来避免。通常基于结构的各阶模态频率和阻尼随空速的变化趋势(即v-f图和v-g图)来预测颤振临界点。确保模态在空速变化过程中的前后对应关系是颤振分析的基础，否则可能会给气弹稳定性判断、颤振模态判别以及颤振抑制设计带来困难。模态跟踪技术旨在保证结构的各阶模态在系统参数变化过程中始终保持正确的前后对应关系，不发生所谓的“模态交叉”现象[1]。因此，发展稳定高效的模态跟踪技术来防止颤振分析中的“模态交叉”是十分必要的。

颤振分析从数学角度上看是一个空速变化时的特征值问题，而模态跟踪本质上是对不同空速下的特征值进行匹配，从而使前后空速下得到的特征值保持正确的对应关系。早期，分析员通常采用人工排序的方法，根据经验判断前后空速下特征值的对应关系，从而得到相对光滑合理的特征值曲线。这样的做法非常繁琐，而且结果的准确性也难以保证。为此，国内外研究人员发展了几种模态跟踪技术，包括：① 利用前后特征值之间的连续性对特征值进行排序[2]，这种方法在步长较长或模态较密集的情况下效果不好；② 基于特征值摄动理论的特征值预测方法[3-5]，即利用矩阵的左右特征向量信息计算特征值相对于空速的导数，从而给出下一空速的特征值预测值，以实现模态跟踪。研究表明该方法的精度较高，但具有较大的计算量；③ 利用系统矩阵右特征向量来计算模态置信度(Modal Assurance Criterion，MAC值)[6-7]，从而实现模态跟踪，此方法虽然简单实用，但经常在颤振点附近出现跟踪错误，即使缩小步长也无法解决。

本文首先探究了传统的MAC值法在应用时出现失效的原因，从数学机理上明确了其存在的缺陷，并研究了一种基于正交检验法的模态跟踪技术。采用悬臂直翼盒模型进行仿真研究，颤振分析结果表明，正交检验法相比于传统的MAC值法更为有效。

1 理论方法

1.1气弹运动方程与基于MAC的模态跟踪技术

在模态坐标下，线性气动弹性系统的颤振运动方程可以写为[8]

(1)

式中：M、D、K均为模态坐标q下的广义质量矩阵、广义阻尼矩阵和广义刚度矩阵；qd=ρV2/2为空气动压；Q为广义非定常气动力系数矩阵，往往是频域下的离散形式。

在气弹伺服控制领域，通常在状态空间模型下进行颤振分析。因此需要获得拉氏域下的非定常气动力矩阵。工程中常用有理多项式拟合的方法将频域气动力延拓至拉氏域。采用Roger法拟合多项式[9]代入式(1)并重写为状态空间的形式

(2)

式(2)可简写为

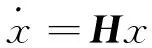
(3)

式(3)的特征值实部表征系统振动衰减率，虚部表征系统振动频率。画出特征值随空速变化的根轨迹图即可分析各空速下的稳定性。由于x中包含了增量状态空间坐标qam，即系统矩阵发生了“扩阶”，使式(3)中多出许多特征值，称其为增根。模态跟踪时，需要将它们与结构模态区分开来。

MAC值法是工程中广泛使用的一种模态跟踪技术，其本质是利用归一化后模态振型的正交性来判断两模态是否一致。为了减少分析自由度，通常将问题转化到模态坐标系下考虑，此时其特征向量之间不仅关于质量和刚度矩阵具有加权正交性，而且具有自正交性。故其特征向量间的MAC值矩阵的计算方法简化为(本节所提到的特征向量均为右特征向量)

(4)

式中，ψi-1和ψi为前后空速下的特征向量以列向量形式组成的两个矩阵。

将MAC值法应用于状态空间模型下的颤振分析，其主要思路为：根据式(4)计算前后空速的MAC值矩阵Si-1,i(由于增根的干扰，该矩阵一般不为方阵)。找到Si-1,i中每一行的最大值，认为其相关的两阶模态是正确对应的。

MAC值法在模态跟踪的前期往往效果较好，但在接近颤振速度时还是容易出现“模态交叉”现象。这是由于颤振分析的研究对象是气动弹性系统，气动力与结构的运动相互耦合。相应地，系统矩阵中就包含气动力的成分，如气动质量、气动刚度、气动阻尼等。这些气动力项是非对称的[10]，导致原本对称的质量、刚度、阻尼矩阵不再对称，从而使系统矩阵失去对称性。根据特征值问题的性质，这意味着其特征向量系同时失去了关于质量、刚度矩阵的加权正交性和自正交性[11]。因此，基于式(4)所进行的模态跟踪方法可能会失效，这点将在算例中予以验证。

1.2正交检验法

针对MAC值法的缺陷，引入系统矩阵的左特征向量系φ来解决系统右特征向量系不正交的问题。调整矩阵S的算法如下

(5)

式中,φi-1为前一空速下系统矩阵的左特征向量矩阵，同样以列向量的形式排列。新的系数矩阵Λi-1,i即为前后空速左右特征向量矩阵的乘积。可以证明，无论系统矩阵是否对称，Λi,i在数学上是一个严格的对角矩阵，即系统矩阵的左右特征向量系是正交的。为了说明这一点，下面给出简单的推导。

任意可对角化的方阵X可以被分解为

X=QEQ-1

(6)

式中,E为对角矩阵，若将式(6)两边同时右乘Q，化为

XQ=QE

(7)

这是一个标准右特征值问题的形式，E对角线上的元素为右特征值，Q的对应列为相应的右特征向量。同理，若将式(6)两边同时左乘Q-1，化为

Q-1X=EQ-1

(8)

这是一个标准左特征值问题的形式，它与右特征值问题具有相同的特征值，Q-1的每一行为其左特征向量。可见，矩阵X的左右特征向量矩阵可以化为互逆的形式。同时也说明矩阵左右特征向量系相互正交。特别的，当X为一实对称矩阵时，有

QTX=EQT

(9)

此时，X的左右特征向量恰好相等，于是右特征向量系自身即可满足正交性。由于模态坐标系下，M和K均为对角矩阵，转化为标准特征值问题后所得的系统矩阵M-1K或K-1M均为对称矩阵，故一般问题均可认为其右特征向量系是正交的。

然而，气弹问题的系统矩阵由于气动力项的影响，是非对称的。因此，由于MAC值法只使用前后风速下的右特征向量进行检验，其MAC值矩阵会丧失正交性。采用引入左特征向量的正交检验法后，新的系数矩阵Λi-1,i相较于Si-1,i具有更明显的对角占优性，特别是在颤振点附近，优势更为明显。

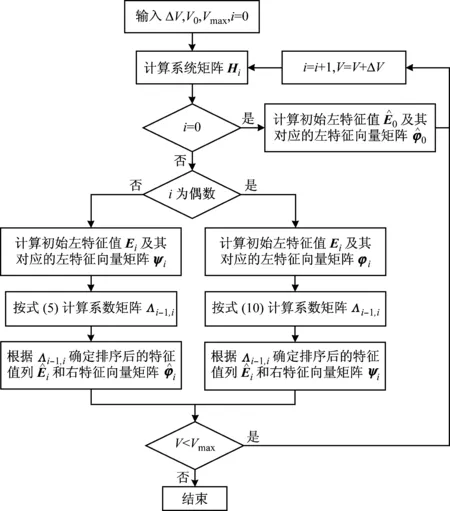
图1 正交检验法的流程图Fig.1 Flowchart of the orthogonality check technique

此外，提出一种高效的系数矩阵计算方法。交换式(5)中左右特征向量矩阵的位置是完全可行的，即

(10)

这样，只需间隔计算各空速下的左右特征向量即可完成模态跟踪，对比原来的式(5)，减少了一半的计算量。正交检验法的具体流程与MAC值法相似，其流程图如图1所示。

2 仿真研究

2.1计算模型

本文选用一悬臂等截面直翼盒作为仿真模型，其几何模型示意图如图2所示。该模型被很多研究者作为验证模型使用，其详细参数见文献[12]。

翼盒的有限元结构建模及其气动力网格划分如图3所示。整个模型分为3个翼段，每个翼段包含两块蒙皮、两块梁腹板和一段翼肋，均设为壳单元；每个翼段的4段梁缘设为杆单元。模型材料设为铝。利用Guyan减缩消除面内位移，以此提高颤振分析的收敛性。前6阶固有频率与文献值的对比如表1所示。模态频率和振型均与文献对应的很好。

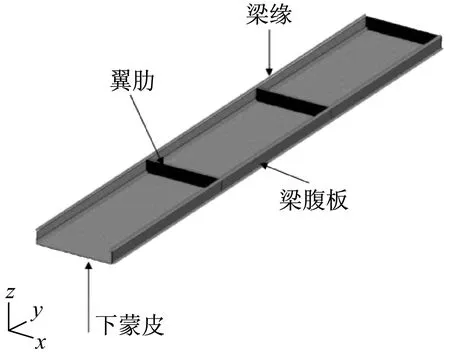
图2 翼盒几何模型(去掉上蒙皮)Fig.2 Geometric model of the wing box (upper skin removed)

2.2计算结果

在Nastran中使用偶极子格网法计算不同减缩频率下的非定常气动力，并采用表面样条插值作用于结构。不考虑结构阻尼，从Nastran中提取计算所得的M、K和Q矩阵。采用Roger法得到拟合的气动力有理多项式，从而将气动弹性方程转化为形如式(2)的状态空间形式。通过对式(3)中系统矩阵H进行特征值求解可以画出其根轨迹图，从而判定系统稳定性。一般认为当某一阶模态特征值实部发生“穿零”，即由负变正时，系统失去稳定性。

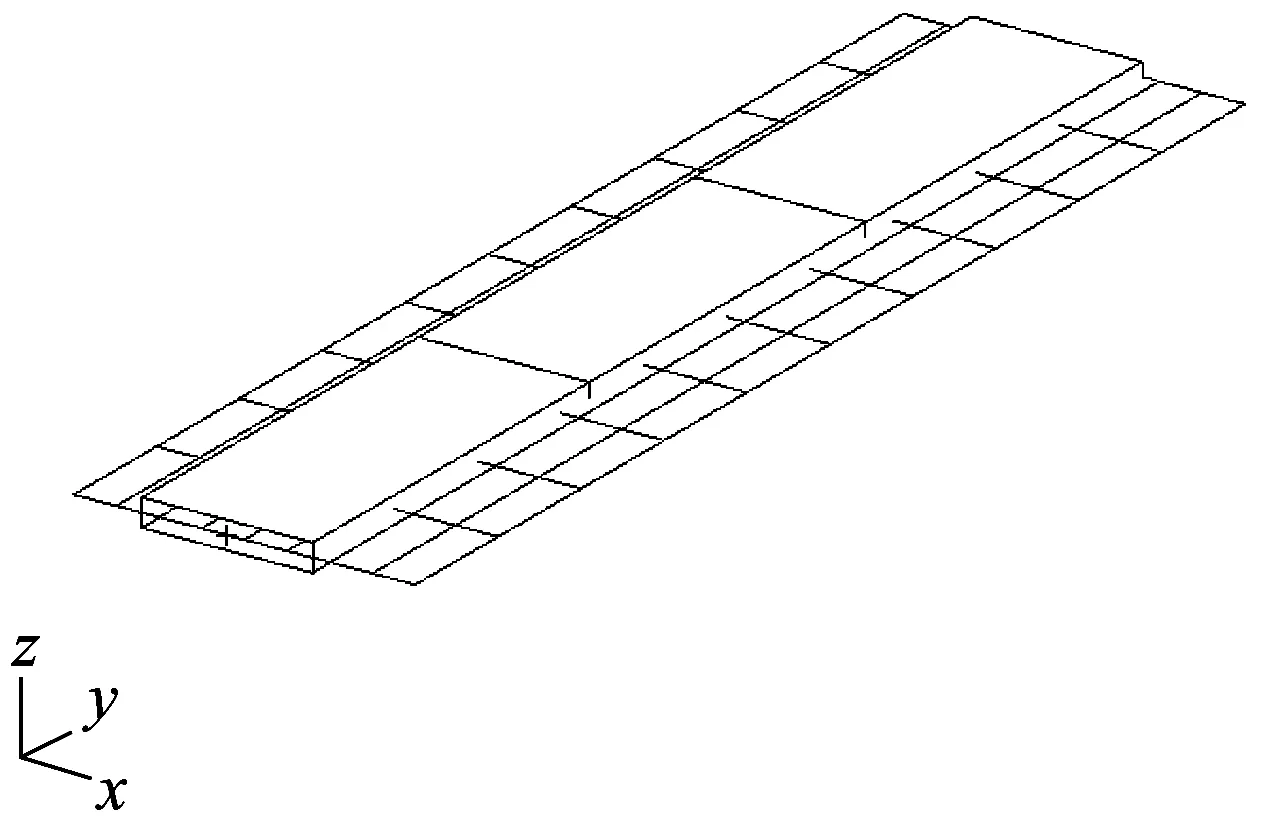
图3 翼盒有限元模型及气动力模型Fig.3 FEM structural & aerodynamic model of the wingbox

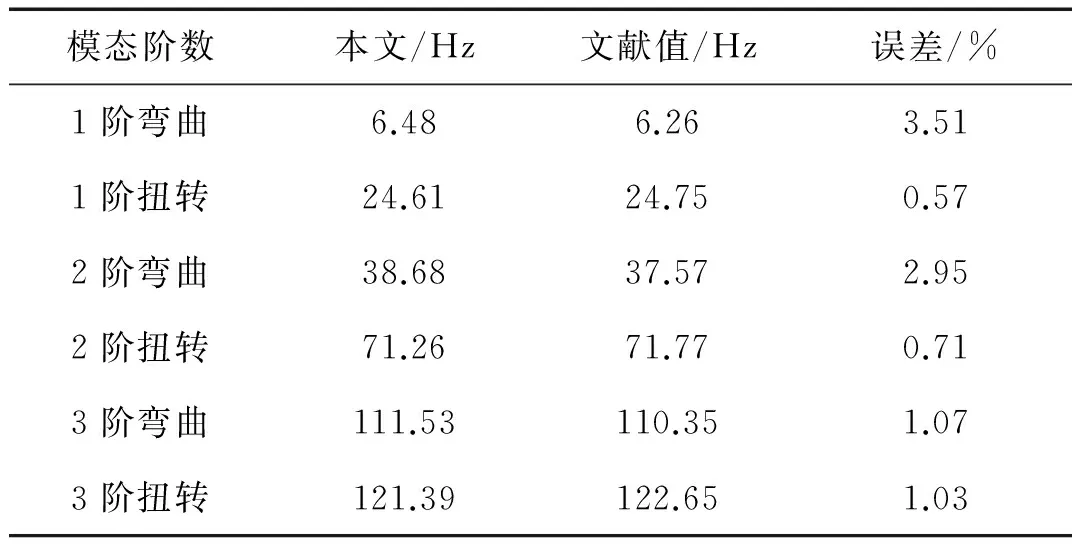
表1 有限元模型前六阶固有频率与文献值的对比Tab.1 The first six natural frequencies of FEM model and the reference values

如果不使用任何模态跟踪方法，只保留虚部为正的特征值，并按虚部从小到大的顺序取前六个特征值作为结构模态，取步长为20 m/s，空速范围为0～450 m/s，分别画出其实部和虚部的根轨迹图如图4、图5所示。可以看出，增根的出现产生了严重的干扰，导致V0之后跟踪到的特征值均为增根，而不对应真实的结构模态。p-k法或者V-g法此类频域方法，由于不受系统“扩阶”的影响，计算得到的特征值总是对应着某阶结构模态，也就是说，模态跟踪只要将所有点正确的连接起来即可。而在状态空间模型下，增根的数量往往是结构模态的特征值的数倍，如果全部画出这些点，肉眼根本无法分辨。因此，可靠高效的模态跟踪技术对根轨迹法来说是不可或缺的。

在相同的输入参数下，分别用MAC值法和正交检验法作出该系统的根轨迹图，如图6～图9所示。MAC值法和正交检验法在2～6阶模态的跟踪上是一致的，由于2阶扭转模态实部“穿零”发生颤振，颤振速度大约为273 m/s，与文献[13]中的结果267 m/s基本一致。而在第1阶模态的跟踪上，MAC值法出现了错误，在280 m/s处开始与第2阶重合。事实上，第1阶模态会在颤振速度之后频率降为0，即出现发散现象，虽然发散速度在这里不是临界速度。文献[13-14]均给出了该发散速度的值，分别为287 m/s和292 m/s。显然，MAC值法无法给出发散速度。从图7、图8可知，正交检验法成功地在颤振速度之后对1阶模态进行跟踪，发散速度为301 m/s。同时，与文献[14]中的根轨迹图进行对比，验证了正交检验法在该例中的准确性。

图4 特征值虚部随空速变化曲线(未使用模态跟踪方法， ΔV=20 m/s)Fig.4 Velocity vs frequencies plot (without mode tracking, ΔV=20 m/s)

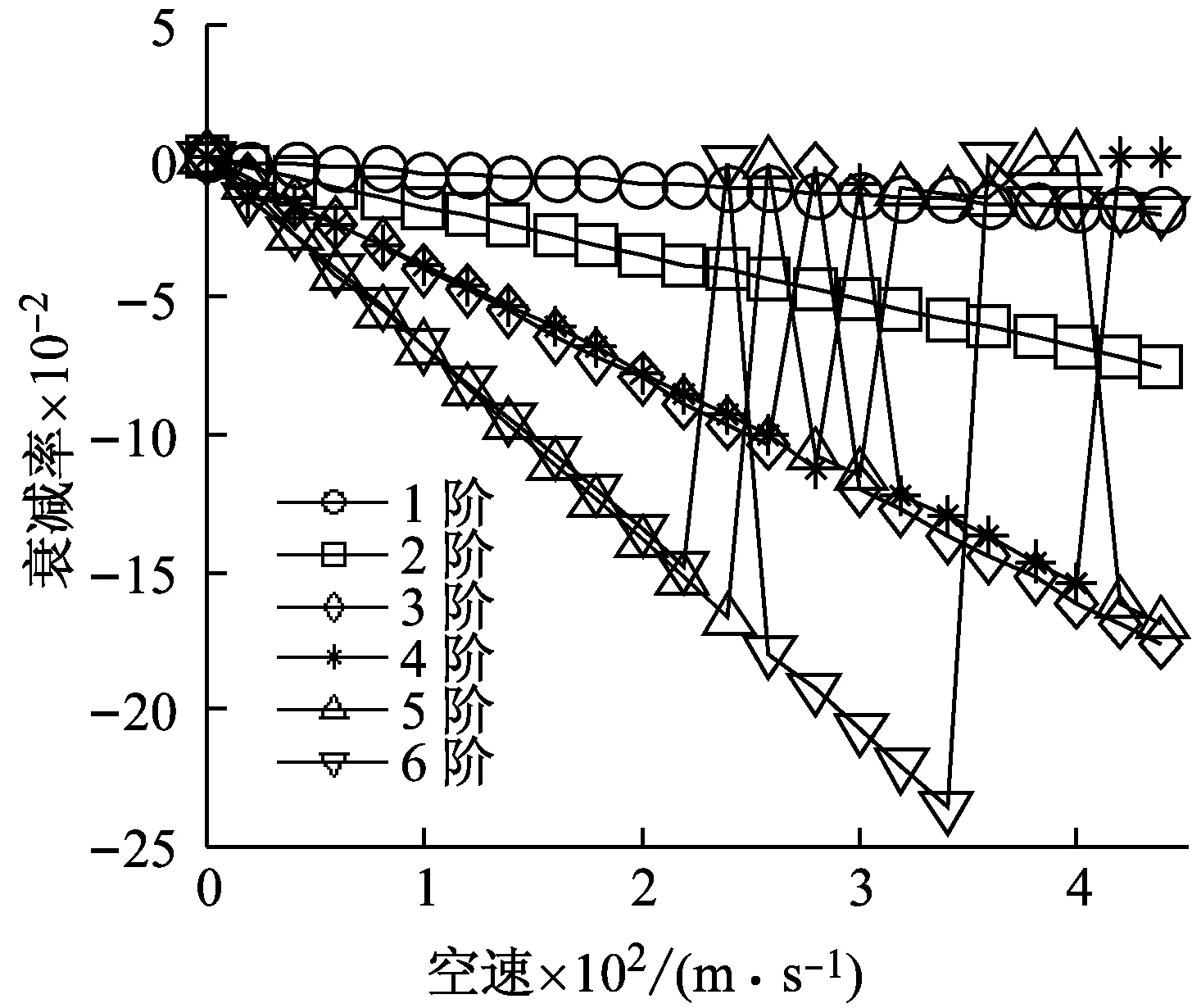
图5 特征值实部随空速变化曲线 (未使用模态跟踪方法， ΔV=20 m/s)Fig.5 Velocity vs decay rate plot (without mode tracking, ΔV=20 m/s)

图6 特征值虚部随空速变化曲线(MAC值法，ΔV=20 m/s)Fig.6 Velocity vs frequencies plot (MAC method, ΔV=20 m/s)

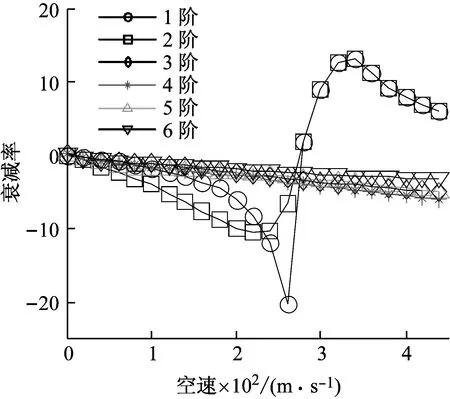
图7 特征值实部随空速变化曲线 (MAC值法，ΔV=20 m/s)Fig.7 Velocity vs decay rate plot (MAC method, ΔV=20 m/s)

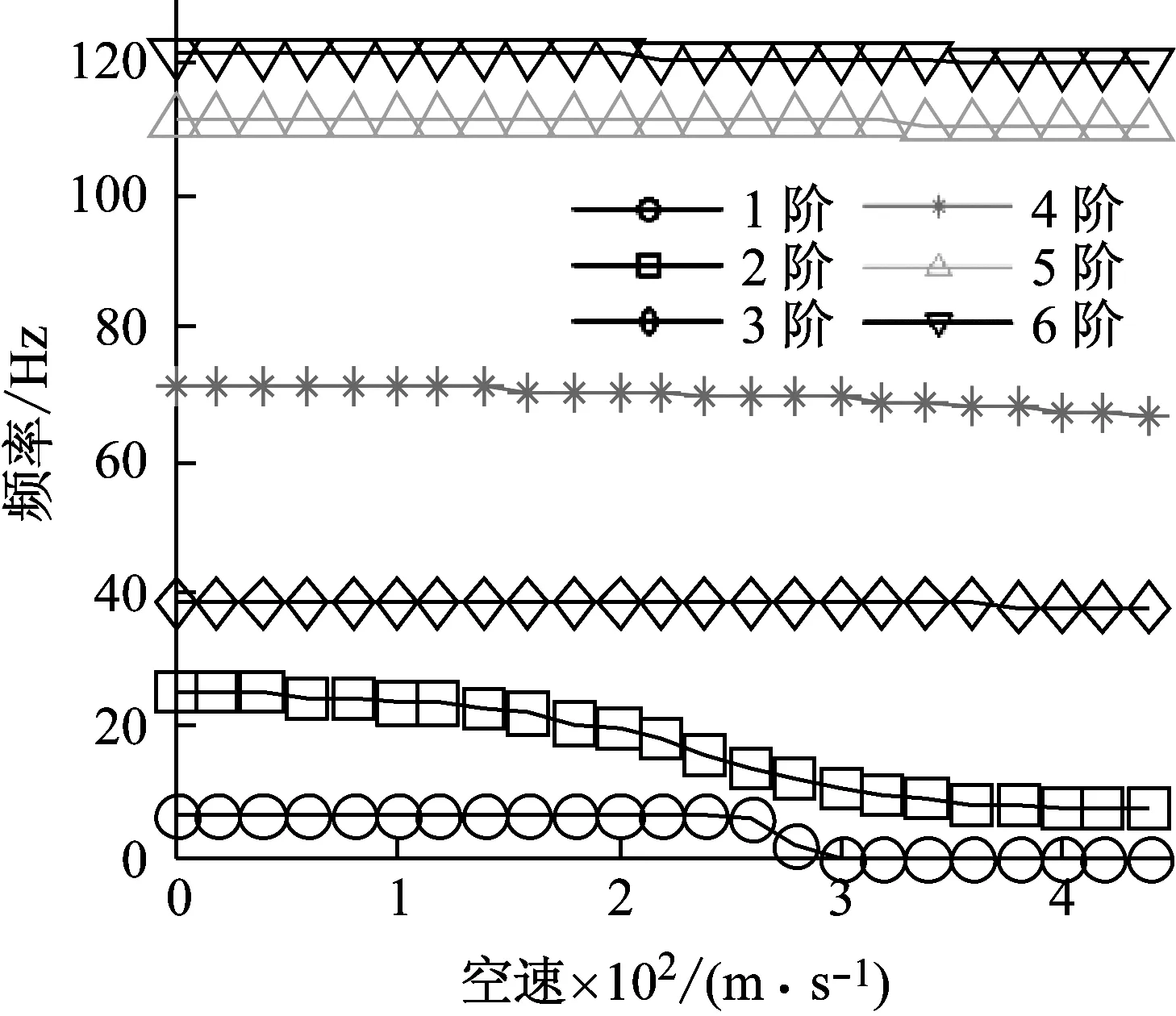
图8 特征值虚部随空速变化曲线(正交检验法，ΔV=20 m/s)Fig.8 Velocity vs frequencies plot (orthogonality check, ΔV=20 m/s)

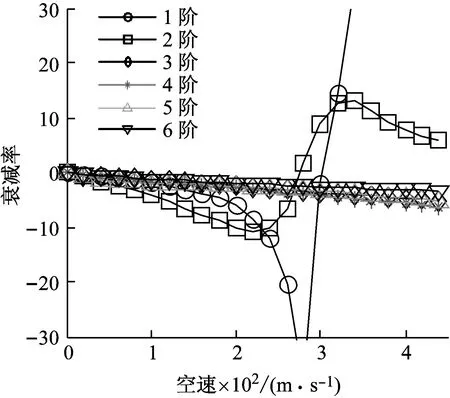
图9 特征值实部随空速变化曲线 (正交检验法，ΔV=20 m/s)Fig.9 Velocity vs decay rate plot (orthogonality check, ΔV=20 m/s)

2.3对比与分析

虽然MAC值法在该例中出现的跟踪错误并没有影响临界速度的判断，但很难保证它在其他工程应用，特别是在气弹优化问题中不出错。可以发现，这种错误往往出现在临近颤振点附近，且在发生模态重合现象的两支或数支模态中。在本算例中，是由一阶弯曲和二阶扭转耦合产生颤振，提取各空速下根据式(4)计算得到的1阶、2阶模态的MAC值Si,i(1,2)，画出其随空速的变化曲线，如图10。可以看到，MAC值随着空速逐渐变大，在颤振点附近达到了最大值，此后又逐渐回落。正如1.1节描述的那样，气动力项使各阶模态的特征向量失去了正交性。对于两阶耦合模态而言，越靠近颤振点，其模态相似程度越高，在颤振点附近几乎变成了同一阶模态，因此其特征向量之间的夹角很小，MAC值接近于1。考虑到空速变化的影响，Si-1,i(1,2)的值在颤振点附近超过了Si-1,i(1,1)，使Si-1,i矩阵丧失了对角占优性，导致了跟踪失败。

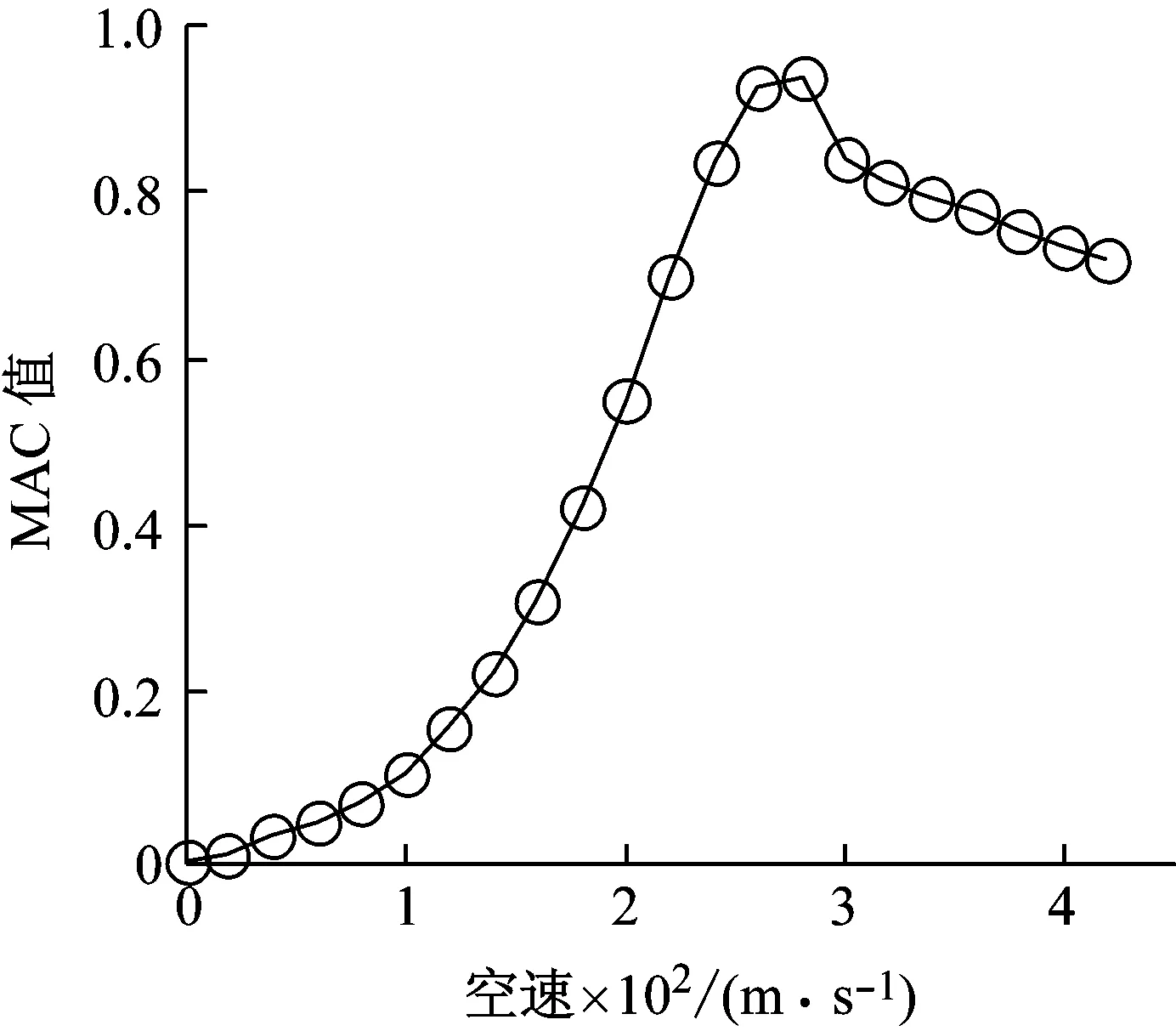
图10 前两阶模态MAC值随空速变化曲线Fig.10 Velocity vs the MAC value of the first two modes plot

为了更直观的体现两种方法在模态跟踪时的表现，分别提取颤振点附近空速为280 m/s处，根据式(4)和式(5)计算得到的前六阶模态之间的系数矩阵。将每行最大值归一化后根据其元素的绝对值画出三维柱状图，如图11、图12所示。从图11可以看出，前两阶模态之间的MAC值与对角线元素大小基本相等。实际上我们通过图6、图7可知，此时Si-1,i(1,2)已经超过了Si-1,i(1,1)，即矩阵丧失了对角占优性。而从图12来看，正交检验法获得的系数矩阵对角占优性依然十分明显。可见，正交检验法在颤振点附近的稳定性明显高于MAC值法。

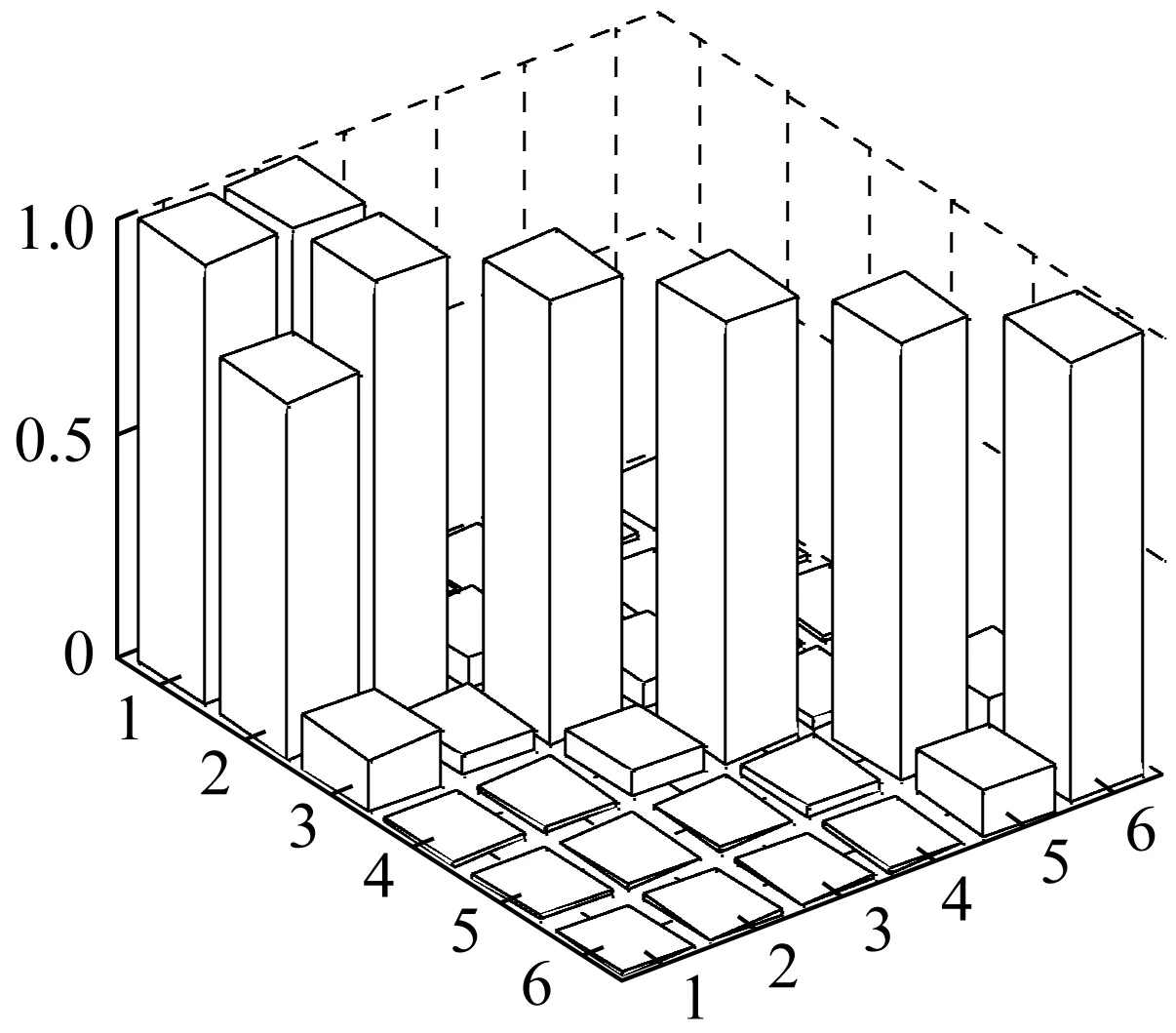
图11 系数矩阵三维柱状图(MAC值法，V=280 m/s)Fig.11 3D bar graph of the coefficient matrix (MAC method, V=280 m/s)

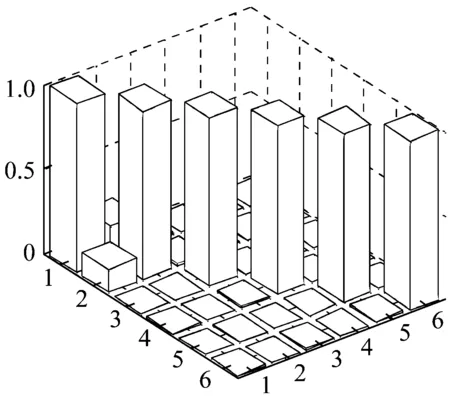
图12 系数矩阵三维柱状图(正交检验法，V=280 m/s)Fig.12 3D bar graph of the coefficient matrix (orthogonality check, V=280 m/s)

一般模态跟踪方法可以考虑减小步长ΔV来避免出错。而本算例中，将步长改为15 m/s甚至10 m/s，MAC值法依然会在颤振点附近失效，情况与图6、图7类似。可见，该算法在颤振点附近的收敛性也不好。而正交检验法在ΔV增至30 m/s时，效果依然稳定，如图13、图14。由1.2节可知，同一空速下系数矩阵是严格的对角阵，因此即使出现跟踪失败，正交检验法通过适当减小步长即可修正错误。

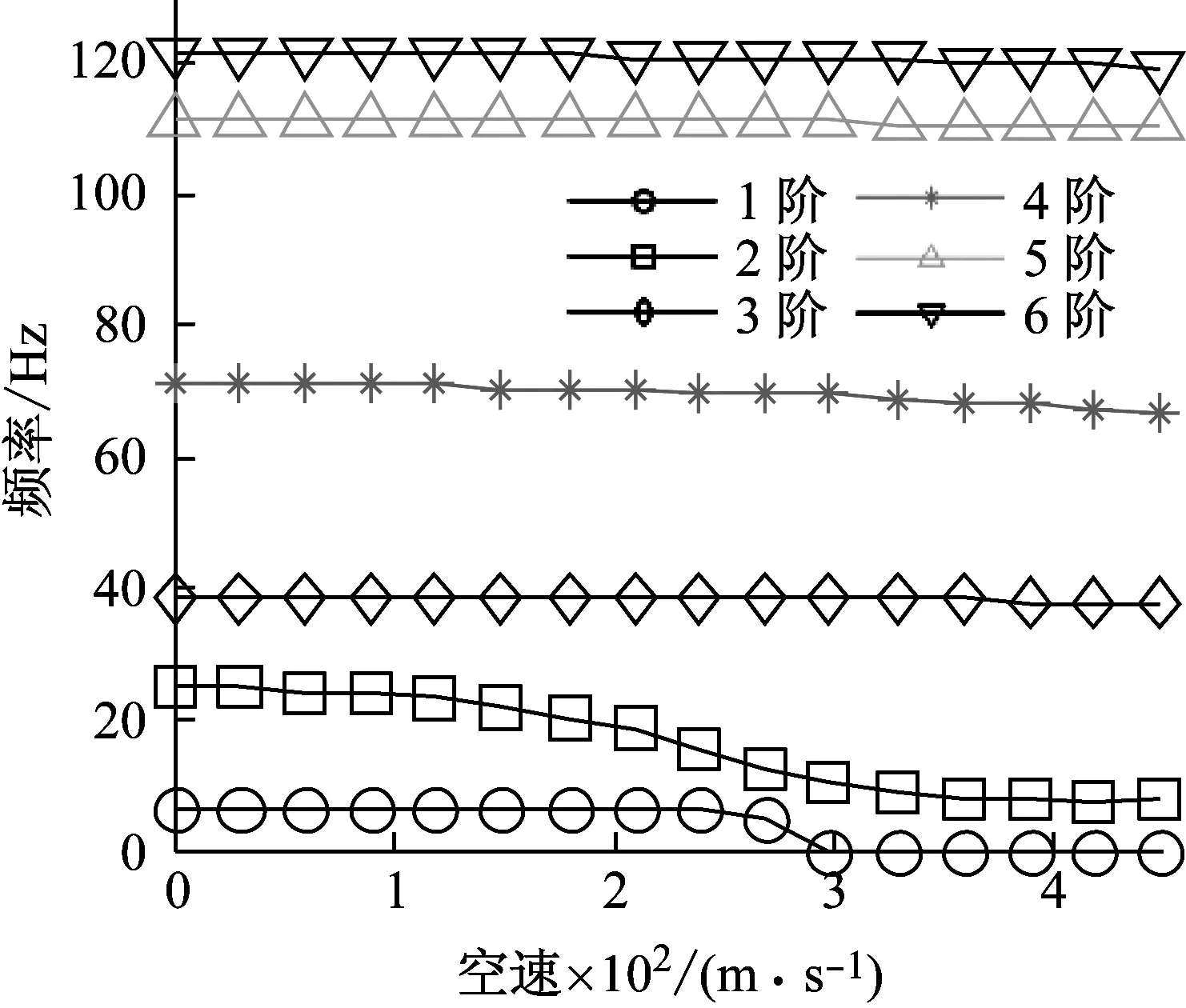
图13 特征值虚部随空速变化曲线(正交检验法，ΔV=30 m/s)Fig.13 Velocity vs frequencies plot (orthogonality check, ΔV=30 m/s)

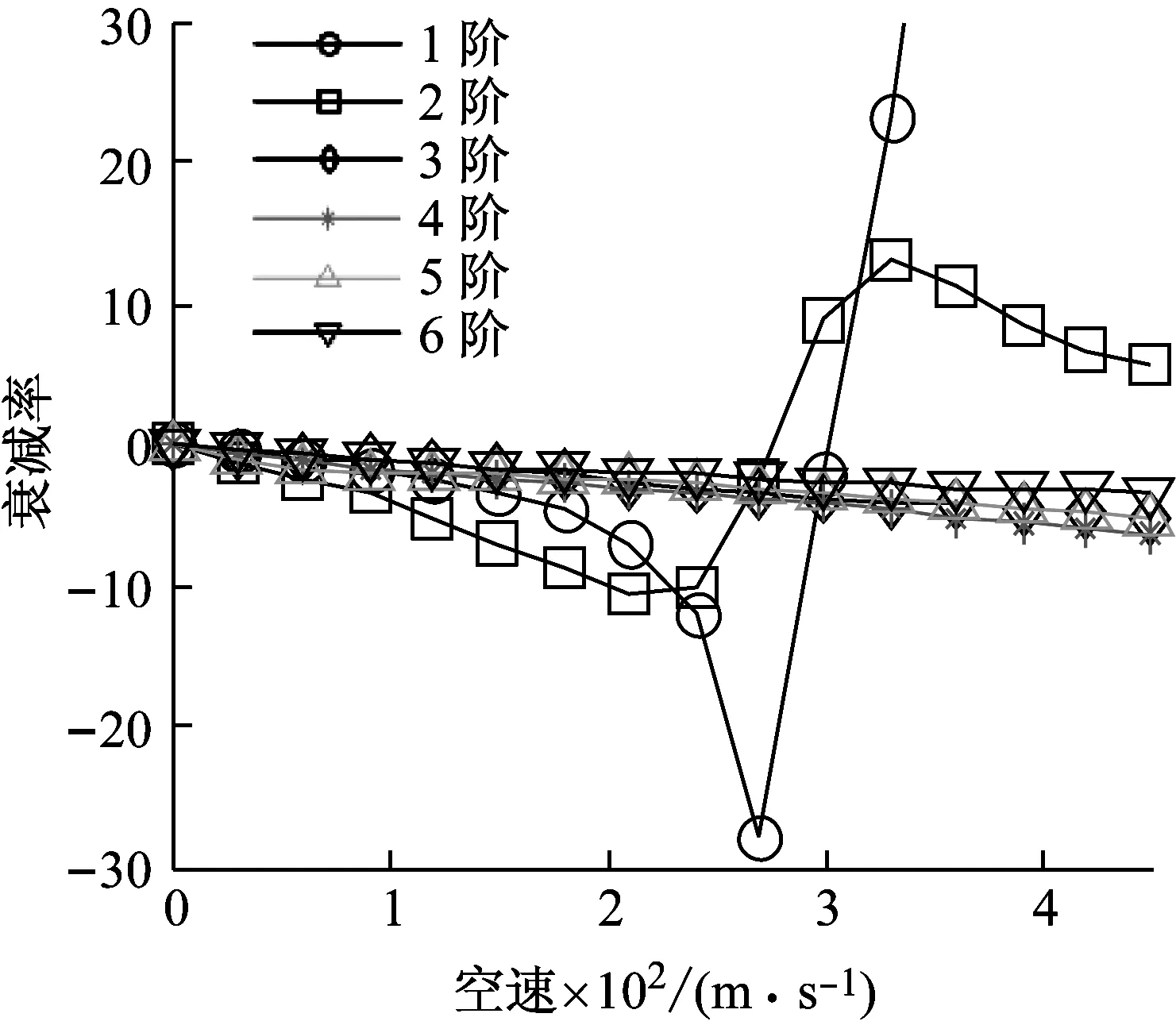
图14 特征值实部随空速变化曲线 (正交检验法，ΔV=30 m/s)Fig.14 Velocity vs decay rate plot (orthogonality check, ΔV=30 m/s)

3 结 论

本文针对传统MAC值法应用于颤振分析时经常出错的问题，从数学机理角度解释了其跟踪失败的原因，并研究了一种基于正交检验法的模态跟踪技术。通过在状态空间模型下的颤振分析算例对两种方法进行对比，得出以下结论：

(1) MAC值矩阵在气弹问题中容易在颤振点附近丧失对角占优性，故MAC值法在颤振分析模态跟踪中可能出错，且很难通过缩小步长来解决。

(2) 正交检验法使系数矩阵的对角占优性大大增加，对步长的要求较低，且对步长具有严格的收敛性。

(3) 从计算效率上来看，正交检验法只需要在每个空速下求解一次特征值问题，与MAC值法相比，在获得更高的模态追踪精度的同时，并未降低运算效率。

[1] ELDRED M S, VENKAYYA V B, ANDERSON W J. Mode tracking issues in structural optimization[J]. AIAA Journal, 1995, 33(10): 1926-1933.

[2] 谢长川, 胡薇薇, 杨超. 颤振分析中的特征值排序问题[J]. 数学的实践与认识, 2007, 37(18): 141-146.

XIE Changchuan, HU Weiwei, YANG Chao. Eigenvalue sorting problem in flutter analysis[J]. Mathematics in Practice and Theory, 2007, 37(18): 141-146.

[3] 吴志刚, 宋晨, 杨超. 颤振分析中的模态跟踪技术[J]. 北京航空航天大学学报, 2010，36(2): 163-167.

WU Zhigang, SONG Chen, YANG Chao. Mode tracking techniques in flutter analysis [J]. Journal of Beijing University of Aeronautics and Astronautics, 2010，36(2): 163-167.

[4] ELDRED M S, VENKAYYA V B, ANDERSON W J. New mode tracking methods in aeroelastic analysis[J]. AIAA Journal, 1995, 33(7): 1292-1299.

[5] 任智毅, 金海波, 丁运亮. 基于气动力分段表达的颤振求解方法与模态跟踪技术的应用[J]. 空气动力学学报, 2014, 32(2): 246-251.

REN Zhiyi, JIN Haibo, DING Yunliang. Flutter analysis based on the piecewise express of aerodynamic forces and the application of mode tracking technology[J]. Acta Aerodynamica Sinica, 2014, 32(2): 246-251.

[6] DESFORGES M J, COOPER J E, WRIGHT J R. Mode tracking during flutter testing using the modal assurance criterion[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 1996, 210(1): 27-37.

[7] GARIFFO J M. Generalized reduced order modeling of aeroservoelastic systems[D]. Los Angeles: University of California, 2013: 35-39.

[8] 管德. 飞机气动弹性力学手册[M]. 北京:航空工业出版社, 1994: 126-142.

[9] 赵永辉. 气动弹性力学与控制[M]. 北京：科学出版社, 2007: 310-315.

[10] WRIGHT J R, COOPER J E, 姚一龙. 飞机气动弹性力学及载荷导论[M]. 上海：上海交通大学出版社, 2010: 161-163.

[11] AFOLABI D，PIDAPARTI R M V，YANG H T Y. Flutter prediction using an eigenvector orientation approach[J]. AIAA Journal, 1998, 36(1): 69-74.

[12] BHATIA K G, RUDISILL C S. Optimization of complex structures to satisfy flutter requirements[J]. AIAA Journal, 1971, 9(8): 1487-1491.

[13] STRIZ A G, VENKAYYA V B. Influence of structural and aerodynamic modeling on flutter analysis[J]. Journal of Aircraft, 1994, 31(5): 1205-1211.

[14] HASAN M. Multidisciplinary design and optimization of a composite wing box[D]. Ankara:Middle East Technical University, 2003: 158-180.

Modetrackingtechniqueinflutteranalysisbasedonthemethodoforthogonalitycheck

JIANG Lingwen1, 2, HANG Xiaochen1, 2, FEI Qingguo1, 2

(1. Jiangsu Key Laboratory of Engineering Mechanics, Nanjing 210096, China;2. Department of Engineering Mechanics, Southeast University, Nanjing 210096, China)

Mode tracking is one of the key problems in flutter analysis. The common method based on the modal assurance criterion frequently fails near the critical point in its application. The mathematical mechanism of the common method was studied, thus revealing its defects in nature. A method based on the orthogonality check was proposed, in which the left eigenvector was introduced. The method was applied to the flutter analysis of an unswept cantilevered wing box in the state space and the root locus of the system was obtained. The numerical results were compared with those of the MAC method and it is validated that the orthogonality check is more effective in mode tracking.

flutter; state space; eigenvector; mode tracking; modal assurance criterion (MAC)

V211

A

10.13465/j.cnki.jvs.2017.19.013

国家自然科学基金(51408389;51438002);江苏省自然科学基金青年基金项目(BK20140281)

基金项目：国家自然科学基金(11572086)；江苏省研究生培养创新工程项目(KYLX15_0092)

2016-03-25 修改稿收到日期：2016-08-15

蒋令闻 男，博士，硕士生,1990年生

费庆国 男，教授，博士生导师,1977年生