多因素组合下发射载体出管速度偏差预估方法

强新伟，汪太琨，常书丽，刘 科

(1.中国船舶重工集团713所，郑州 450015；2.河南省水下智能装备重点实验室，郑州 450015)

2017-01-20；

2017-04-07。

强新伟(1977—),男,研究员,研究方向为水下发射动力技术。E-mailqxwgxw@163.com

多因素组合下发射载体出管速度偏差预估方法

强新伟1,2，汪太琨1,2，常书丽1,2，刘 科1,2

(1.中国船舶重工集团713所，郑州 450015；2.河南省水下智能装备重点实验室，郑州 450015)

运用极限偏差、合成标准差、统计分析、蒙特卡洛仿真等多种预估方法，对发射载体出管速度偏差进行对比分析。分析结果表明，极限偏差法工程应用成熟，但预估结果偏于保守，适用于影响因素尚未认知完全的工程型号；对于影响因素比较明确的系统，运用统计分析法、合成标准差法得到的发射载体出管速度预估值一致性好，方法简单，且具有较高的准确性；蒙特卡洛法计算过程复杂，可通过大量仿真计算获取出管速度的分布特性，得到对应不同指标的分布概率，相比其他几种方法，计算结果更加科学、合理。工程型号应用时，可根据实际需要组合使用上述方法进行发射载体出管速度偏差预估分析。

出管速度偏差预估；极限偏差法；合成标准差；蒙特卡洛

0 引言

采用燃气蒸汽式发射动力装置进行载体水下发射技术成熟、稳定可靠，且不占用发射筒底空间，目前已得到了广泛的应用。在进行型号设计时，出管速度是发射动力装置的重要内弹道特征参数，主要为发射载体水中弹道提供初始参数，使发射载体获得初始动能。对于采用水下弹射、水面点火方式的发射载体，其出管速度偏差直接影响发射载体出水姿态的稳定性，进而影响到发射载体点火安全性。内弹道参数预估就是采用理论分析的方式，根据特定的初始条件和设计的工作状态对发射载体筒内运动过程进行计算，获得发射载体出管速度等运动参数，以判定所设计的工作状态能否满足指标要求。水下发射是一个复杂的物理化学过程，内弹道理论预估与实际结果必然存在一定差异。实践表明，同一型号发射动力装置，在相同试验条件下的内弹道参数呈随机性散布。显然，内弹道预估存在一定的预估偏差。

国内赵险峰、李咸海等在充分研究发射动力装置工作原理的基础上运用质量、能量等守恒定律、气体状态方程、导弹运动方程等对发射筒内做工的工质气体进行分析，建立了发射内弹道的理论计算模型，对导弹的运动过程进行描述[1-2]；赵世平、肖虎斌、沈国等应用CFD技术对发射动力装置工作过程进行流场数值模拟[3-4]；惠卫华等对燃气发生器内弹道性能进行了预估研究[5]；都军民、常书丽等分别采用蒙特卡洛方法对内弹道参数进行分析[6-7]；国外对燃气蒸汽式弹射技术也进行过大量研究[8-9]。

目前，在工程型号应用中，基于一定假设条件下建立了一套发射载体出管速度偏差预估计算方法，虽可满足总体要求，但计算结果偏于保守。随着新型号应用，发射载体出管速度影响因素更多，且总体对发射载体出管速度偏差要求更高，对出管速度偏差分布规律要求细化。本文基于多年研制经验，通过开展发射载体出管速度偏差多种预估方法对比研究，并结合大量工程试验数据分别进行发射载体出管速度计算，对比分析各方法预估精度，从而为工程中多因素情况下发射载体出管速度偏差特性预估提供依据与参考。

1 出管速度偏差影响因素

某型燃气蒸汽式发射动力系统主要由点火保险机构、燃气发生器、冷却器、弯管等部分组成，如图1所示。发射载体水下发射时，点火保险机构点火，燃气发生器内装药燃烧产生高温高压燃气，燃气经过分流管的分流在冷却器内喷水管内外形成喷水压差，将冷却水经过喷水孔喷入喷水区。在喷水区内冷却水与高温高压燃气发生剧烈掺混，水吸热汽化，达到降温和调能的目的，掺混后的混合气体经过动力弯管流入发射筒底，在筒底建立压力膨胀做功，将发射载体弹射出去。

经分析，出管速度偏差与发射载体、发射平台、发射装置、水下发射环境等多方面有关，涉及设计、生产、使用、测试、数据处理等多个环节。此外，还有一些目前认识不到的因素(如洋流、发射平台航速所引起的横向载荷等影响)也会影响发射载体出管速度分布。因此，发射载体出管速度偏差影响因素主要包括以下几方面：

(1)内弹道计算相关参数带来的偏差：涉及发射装置、发射载体、发射平台、水下发射环境等方面；

(2)内弹道数学模型带来的偏差；

(3)数据测量和处理方法带来的偏差。

2 内弹道计算模型

由于发射动力装置工作过程复杂，影响因素众多，在理论分析时，将发射动力装置工作过程进行简化，抓住关键环节，建立了其工作过程的主要控制方程组[2]。

燃气发生器内部压力计算方程：

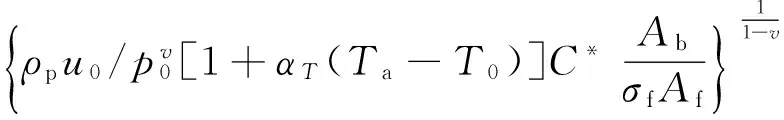
通过燃气发生器喉部流出的燃气质量：

冷却器内部包含了高温高压燃气湍流流动、冷却水喷注、水与燃气掺混雾化等复杂的传热和相变等过程，具体过程已不能用控制方程描述，但通过小孔流量关系可计算出通过冷却器喷注与燃气掺混的水量：

能量守恒方程：

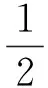
气体状态方程：

导弹运动方程：

Ma=ptSt-F

F=Mg+Fz+fptSt+p0St+pg[HSt-lSm]+

3 出管速度偏差预估方法

3.1 极限偏差法

假设运用发射内弹道进行计算时，与出管速度偏差有关设计参数及波动范围如下：

(1)装药燃速：Ur±ΔUr。

(2)发射深度：H±ΔH。

(3)发射载体质量：M±ΔM。

(4)发射载体发射摩擦力系数：z±Δz。

(5)冷却水初温：Tl±ΔTl。

(6)经验修正系数：X±ΔX。

将上述各影响因素的额定值代入发射内弹道方程进行预估计算，可得到出管速度额定值。

将包含有使出管速度向上偏的各影响因素极限值代入发射内弹道方程进行预估计算，可得到出管速度上偏差。

将包含有使出管速度向下偏的各影响因素极限值均代入发射内弹道方程进行计算，可得到出管速度下偏差,即：

Ve=F(Ur,H,M,z,T1,X)

Ve+ΔVe上=F(Ur+ΔUr,H-ΔH,M-ΔM，

z-Δz,T1+ΔT1,X+ΔX)

Ve-ΔVe下=F(Ur-ΔUr,H+ΔH,M+ΔM，

z+Δz,T1-ΔT1,X-ΔX)

上述计算中未考虑发射内弹道数学模型、测试及数据处理环节带来的偏差，但从概率论的角度，所有影响因素同时走极限值，且均向同一方向偏离在实际发射过程中是一个小概率事件。因此，该计算方法得到的预估结果趋于保守，但从另外一个角度讲，极限偏差法得到的计算结果也最可靠。

3.2 合成标准差法

运用该方法之前，必须获取出筒速度相关设计参数在各自极限波动范围内变化时分别引起的出筒速度变化量。

以装药燃速U为例，其在波动范围内分别取上、下限时对出筒速度的单因素影响量计算方法如下：

ΔVe(ΔUr)上=F((Ur+(ΔUr)上),H,M,z,T1,X)-

F(Ur,H,M,z,T1,X)

ΔVe(ΔUr)下=F(Ur,H,M,z,T1,X)-

F((Ur-(ΔUr)下),H,M,z,T1,X)

以此类推，可分别求出H、M、z、Tl、X等参数对出筒速度的单因素影响量。经工程验证，上述各因素是独立的随机变量，各因素对出管速度影响量近似服从正态分布，则可按如下方法求其合成标准差[10-12]。

假设各影响因素极限波动范围引起出管速度变化量如下：

(1)装药燃速

ΔVe(ΔUr)上=3×σ1上

ΔVe(ΔUr)下=3×σ1下

(2)发射深度

ΔVe(ΔH)上=3×σ2上

ΔVe(ΔH)下=3×σ2下

(3)发射载体质量

ΔVe(ΔM)上=3×σ3上

ΔVe(ΔM)下=3×σ3下

(4)发射载体发射摩擦力系数

ΔVe(Δz)上=3×σ4上

ΔVe(Δz)下=3×σ4下

(5)冷却水初温

ΔVe(ΔT1)上=3×σ5上

ΔVe(ΔT1)下=3×σ5下

(6)经验修正系数

ΔVe(ΔX)上=3×σ6上

ΔVe(ΔX)下=3×σ6下

依据合成标准差法得到出管速度上、下预估偏差:

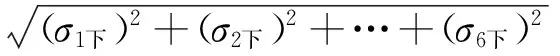
该种法要求对相关影响因素尽可能辨识完整、全面，因此具体工程应用时还应考虑模型、测量等误差因素(可通过试验数据统计或理论分析获取)。

3.3 统计分析法

此方法基于技术状态相近且具有一定数量的试验子样。单发试验中，出管速度预估值与实测值之间差值称为预估偏差。该预估偏差除了包含发射内弹道数学模型、测试及数据处理环节带来偏差外，还包括预估计算时设计参数与实际试验中不一致带来的偏差。经验证，出管速度预估偏差试验子样服从正态分布N(μ，σ2)，则对于相近技术状态的下一发试验而言，在获取其出管速度预估额定值Ve后，其预估偏差及分布概率为出管速度处于(Ve-μ)±1×σ范围内的概率为68.26%；出管速度处于(Ve-μ)±2×σ范围内的概率为95.44%；出管速度处于(Ve-μ)±3×σ范围内的概率为99.73%。

3.4 蒙特卡洛法

蒙特卡洛(Monte Carlo)方法又称为随机模拟方法(Random simulation)，是一类通过随机变量的统计实验(或者随机模拟)，求解数学、工程技术问题近似解的数值方法。

运用该方法进行仿真计算时，首先须对发射内弹道数学模型计算结果与实际试验结果的一致性进行检验。仿真时，首先分析试验中出管速度偏差实际各影响因素及波动范围；然后，将出管速度偏差影响因素在其取值范围内按照各自的分布规律进行一定数量的初始参数随机抽样；最后，将所有参数汇总并运用发射内弹道数学模型进行计算，进而获取足够数量的出管速度仿真值及其分布规律。

在进行正态分布检验后，即可获取其均值μ与方差σ2。通过计算和查正态分布表即可获得发射载体出管速度不同偏差下的分布概率。

4 各方法预估值对比分析

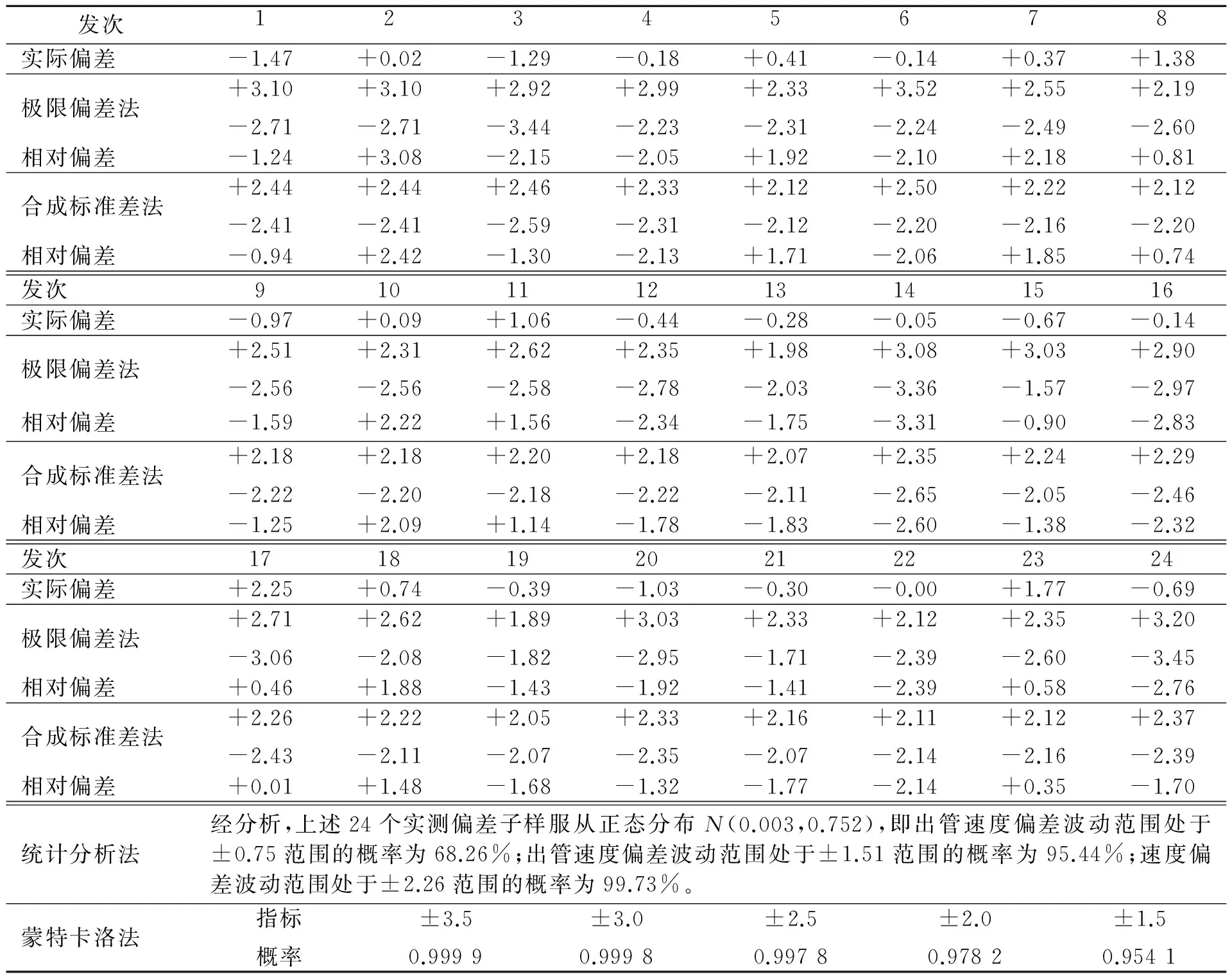
以某型号发射动力系统研制期间相同技术状态试验数据为基础，分别运用上述方法对24发不同发射条件下的水下试验进行出管速度预估计算，并与试验中实际获得的偏差进行了对比分析见表1、图2。表1中，相对偏差为不同方法得到的预估上(下)限与实际偏差的差值：实际偏差为正，取上限，反之取下限。

发次12345678实际偏差-1.47+0.02-1.29-0.18+0.41-0.14+0.37+1.38极限偏差法+3.10-2.71+3.10-2.71+2.92-3.44+2.99-2.23+2.33-2.31+3.52-2.24+2.55-2.49+2.19-2.60相对偏差-1.24+3.08-2.15-2.05+1.92-2.10+2.18+0.81合成标准差法+2.44-2.41+2.44-2.41+2.46-2.59+2.33-2.31+2.12-2.12+2.50-2.20+2.22-2.16+2.12-2.20相对偏差-0.94+2.42-1.30-2.13+1.71-2.06+1.85+0.74发次910111213141516实际偏差-0.97+0.09+1.06-0.44-0.28-0.05-0.67-0.14极限偏差法+2.51-2.56+2.31-2.56+2.62-2.58+2.35-2.78+1.98-2.03+3.08-3.36+3.03-1.57+2.90-2.97相对偏差-1.59+2.22+1.56-2.34-1.75-3.31-0.90-2.83合成标准差法+2.18-2.22+2.18-2.20+2.20-2.18+2.18-2.22+2.07-2.11+2.35-2.65+2.24-2.05+2.29-2.46相对偏差-1.25+2.09+1.14-1.78-1.83-2.60-1.38-2.32发次1718192021222324实际偏差+2.25+0.74-0.39-1.03-0.30-0.00+1.77-0.69极限偏差法+2.71-3.06+2.62-2.08+1.89-1.82+3.03-2.95+2.33-1.71+2.12-2.39+2.35-2.60+3.20-3.45相对偏差+0.46+1.88-1.43-1.92-1.41-2.39+0.58-2.76合成标准差法+2.26-2.43+2.22-2.11+2.05-2.07+2.33-2.35+2.16-2.07+2.11-2.14+2.12-2.16+2.37-2.39相对偏差+0.01+1.48-1.68-1.32-1.77-2.14+0.35-1.70统计分析法经分析,上述24个实测偏差子样服从正态分布N(0.003,0.752),即出管速度偏差波动范围处于±0.75范围的概率为68.26%;出管速度偏差波动范围处于±1.51范围的概率为95.44%;速度偏差波动范围处于±2.26范围的概率为99.73%。蒙特卡洛法指标概率±3.50.9999±3.00.9998±2.50.9978±2.00.9782±1.50.9541

从表1、图2可看出，发射载体出管速度实测偏差大部分在±2 m/s范围内，第17发(实际条件与预估取值偏差较大，再加上测试偏差等综合影响所致)达到2.25 m/s，但整体均在极限偏差法、合成标准差法、统计分析法得到的出管速度偏差预估范围包络内。

其中，合成标准差法预估偏差范围与统计分析法±3σ到的预估范围基本相当，即在±2.26 m/s范围内分布概率达到99.73%左右，可以足工程应用需求。

相对而言，极限偏差法只考虑发射内弹道设计参数偏差情况下预估偏差范围大部分在±3 m/s左右，个别发次达到3.5 m/s，整体计算结果相对偏保守。但与此同时，对试验中可能出现的未知因素引起的出管速度异常偏差的弥补性更强(第17发实际偏差已达到统计分析法和合成标准差法计算临界值，但小于极限偏差法临界值)。

运用蒙特卡洛法对上述水下试验进行大批量抽样仿真计算，得到的发射载体出管速度概率密度分布函数如图3所示。该方法可得到发射载体出管速度对应不同指标下的分布概率(见表1)，可为开展发射内弹道参数分布规律详细研究提供重要手段。

对比表1中不同方法与实际偏差的相对偏差可知：

(1)极限偏差法的相对偏差波动范围为-3.31～+3.08 m/s，合成标准差法的相对偏差波动范围为-2.60～+2.42 m/s，后者预估准确性相对优于前者。

(2)统计分析法和蒙特卡洛法的预估范围均与概率有关。经分析，对应99.8%情况下预估值的相对偏差波动范围约为-2.50～+2.48 m/s，与合成标准差预估精度基本相当。

5 结论

(1)多因素组合下，发射载体出管速度预估历来备受总体关注，本文基于多年研制经验，通过对极限偏差法、合成标准差法、统计分析法、蒙特卡洛法等多种预估方法进行分析研究及工程实例验证，对比分析了各方法预估精度及各自适用范围，可为工程中多因素情况下发射载体出管速度偏差特性预估提供依据与参考。

(2)具体工程应用中，可根据实际需求组合使用上述方法，进行发射载体出管速度偏差预估分析，相互验证的同时，进一步提高预估的准确性与合理性，从而有效支撑多种潜射武器系统发射载体出管速度偏差预估。

[1] 李咸海，王俊杰.潜地导弹发射动力系统[M].哈尔滨：哈尔滨工程大学出版社，2000.

[2] 赵险峰，王俊杰.潜地弹道导弹发射系统内弹道学[M].哈尔滨：哈尔滨工程大学出版社，2000.

[3] 肖虎斌，赵世平.燃气蒸汽式发射动力装置复杂内流场数值模拟[J].固体火箭技术，2009，32(4)：392-395.

[4] 惠卫华，鲍福廷，刘旸.考虑低燃温燃气发生器试验的弹射器内弹道性能预示[J].固体火箭技术，2013,36(6):715-719.

[5] 沈国.蒸汽弹射系统内弹道数值模拟与参数设计[D].南京:南京理工大学，2011.

[6] 都军民，汪太琨.利用蒙特卡洛方法对导弹筒内弹道参数的分布进行分析[J].弹舰与制导学报，2002，22(4):45-47.

[7] 常书丽,吕翔，王彦涛等.基于蒙特卡洛方法的燃气蒸汽式发射装置内弹道参数分析方法[J].固体火箭技术，2016，39(6)：857-862.

[8] Edquist C T.Prediction of the launch pulse for gas generator launched missiles[R].AIAA 88-3290.

[9] Edquist C T， Romine G L.Canister gas dynamics of gas generator launched missiles[R].AIAA 80-1186.

[10] 李良巧，顾唯明.机械可靠性设计与分析[M].北京：国防工业出版社，1998.

[11] 吕翔，李江，陈剑，等.变深度水下发射系统内弹道实验研究[J].固体火箭技术，2012，35(1):24-28.

[12] 赵世平.潜地弹道导弹变深度发射动力系统有用能调节机理研究[D].西安：西北工业大学，2007.

Predictionmethodaboutthedeviationcharacteristicsofthelaunchvehicle'stube-exitvelocityundermultifactorcombination

QIANG Xin-wei1,2， WANG Tai-kun1,2，CHANG Shu-li1,2，LIU Ke1,2

(1.No.713 Institute,China Shipbuilding Industry Corporation，Zhengzhou 450015，China;2.Henan Key Laboratory of Underwater Intelligent Equipment,Zhengzhou 450015,China)

This text utilized the limit deviation method,synthesis method of standard deviation,statistical analysis,Monte-Carlo method to make contrastive analysis for the deviation of the tube-exit velocity.The limit deviation method was ripe in the engineering application,but this method inclined to conservative,and can only be used in the engineering whose influence factors wasn't completely cognized.For the system with specified influence factors,the tube-exit velocity of the launched vehicle achieved through statistical analysis and synthetic method of standard deviation was accordant.These methods were simple with superior accuracy.Monte-Carlo method's process of computing was complicated,which could achieve distributive characteristics of the tube-exit velocity through a large number of computing.One could get the distributive probability about different indicators,where the computing results were much more scientific and rational comparative to the other methods.When applying this method in engineering, one could combine these methods under the necessity to predicting the deviation of the tube-exit velocity.

predicting the deviation of the tube-exit velocity；limit deviation method;synthetic method of a standard deviation;Monte-Carlo

V553

A

1006-2793(2017)05-0666-05

10.7673/j.issn.1006-2793.2017.05.023

(编辑：吕耀辉)