带鸭翼的弹性高超声速飞行器非线性控制
2017-11-06陈万春马洪忠杨志红
祝 姣,陈万春,马洪忠,杨志红
(1. 北京航空航天大学 宇航学院,北京 100191;2. 中国航天科工集团公司三院无人机技术研究所,北京 100074;3. 北京空天技术研究所,北京 100074)
2016-06-12;
2017-07-05。
祝姣(1988—),女,博士,研究方向为高超声速飞行器动力学建模与控制。E-mailzhujiao0406@126.com
带鸭翼的弹性高超声速飞行器非线性控制
祝 姣1,3,陈万春1,马洪忠2,杨志红3
(1. 北京航空航天大学 宇航学院,北京 100191;
2. 中国航天科工集团公司三院无人机技术研究所,北京 100074;
3. 北京空天技术研究所,北京 100074)
高超声速飞行器纵向静不稳定、非最小相位和突出的弹性效应等特性给飞行器控制系统设计带来严峻挑战。针对该问题,文中采取鸭翼作为附加俯仰控制舵面与升降舵进行联动控制的策略,以改善高超声速飞行器的非最小相位特性和严重的弹性效应,从而达到提高控制性能的目的。首先,给出了考虑弹性模态的高超声速飞行器动力学模型;其次,研究了鸭翼对飞行器非最小相位特性以及弹性模态响应的影响,并给出合适的鸭翼布局位置和鸭翼/升降舵联动增益参数;最后,采用基于反馈线性化方法和LQR理论的非线性控制器对弹性飞行器进行控制,对比分析了鸭翼联动控制对闭环控制性能的改善作用。研究结果表明,合理的鸭翼配置可以缓解系统的非最小相位特性带来的不利影响,同时避免了控制输入对特定弹性模态的激励,从而达到提高弹性高超声速飞行器控制性能的目的。
高超声速飞行器;鸭翼;非最小相位;弹性模态;反馈线性化;非线性控制
0 引言
吸气式高超声速飞行器由于采取机体/发动机一体化设计,推力作用线在质心之下,前体升力和发动机推力会产生较大的抬头力矩,造成飞行器的俯仰通道静不稳定[1-2]。而采用安装于机体尾部的大尺寸升降舵面进行俯仰通道控制时,必然会带来严重的非最小相位问题。飞行器的静不稳定特性和非最小相位特性分别构成了控制系统设计带宽的下限和上限约束,严重限制了控制系统的设计空间和可达闭环性能[3]。高超声速飞行器一般采取细长体构型和轻质结构设计,导致弹体结构频率较低[4],而静不稳定特性要求较高的控制频带,导致低阶弹性模态频率与控制系统带宽交叠,以至于控制指令能够激励弹性振动,带来严重的弹性稳定问题。
不考虑防热等其他实际因素的影响,单纯从控制角度来看,采取鸭翼作为冗余的俯仰控制舵面,不仅可以缓解飞行器的非最小相位特性,改善飞行器低速时的操纵性[5],还能给控制器设计提供更大的设计空间,提高飞行器的可达控制性能。文献[2]研究了鸭翼对飞行器航迹动力学的影响,通过鸭翼与升降舵联动控制来提高系统右半平面传输零点的频率,使得系统不稳定零极点之间的频率间隔加大,从而缓解甚至消除非最小相位特性对控制系统的限制。文献[6]研究了采用鸭翼作为附加执行机构,以消除控制舵面对升力的气动耦合项。由于弹性机体振动的主要激励源来自于舵面产生的控制力,文献[7]指出,通过采用多舵面联合控制,可实现在满足对刚体运动控制的同时避免激励指定的低阶弹性运动模态,从而实现提高飞行器飞行品质的目的。文献[8]研究了弹性高超声速飞行器的鲁棒输出反馈控制问题,鸭翼作为额外的控制舵面,结合角速率反馈,达到镇定飞行器的不稳定零动态的目的。文献[9]采用鸭翼联动控制策略,用于消去模型的非最小相位特性,在此基础上设计了基于反步法的鲁棒自适应控制。
综上所述,采用鸭翼作为附加的控制舵面,可极大程度地缓解飞行器控制系统设计所面临的困难。本文借鉴了文献[2,6]等提出的附加鸭翼联动控制,采取合理的配置策略,来同时达到消除非最小相位特性和抑制弹性模态的目的,从而提高高超声速飞行器非线性控制器性能。
1 弹性高超声速飞行器模型
本文借鉴文献[4]的动力学模型建模方法,该模型采用激波-膨胀波理论计算定常气动力,采用当地活塞流理论计算弹性振动带来的非定常气动力。结构动力学建模时采用自由梁假设条件,因此飞行器刚体弹性之间不存在惯性耦合,刚弹耦合只体现在气动力和广义力中。弹性高超声速飞行器纵向运动方程如下:
(1)

基于基础理论所推导的模型中力和力矩的计算过于复杂,难以开展模型特性分析和控制器设计。因此,文献[9]对初始模型中的气动力和力矩进行了曲线拟合,得到力和力矩的简化表达式如下:
(2)
其中,zT为推力偏心力臂,各气动力系数和力矩系数如下式给出:
(3)
由式(2)、式(3)可知,鸭翼对飞行器的动力学特性影响主要表现在其对升力L、阻力D、俯仰力矩M以及弹性模态广义力Ni的额外贡献。
对式(1)进行配平并进行小扰动线性化,图1为在h=25 908 m、V=2347.6 m/s时,原系统开环极点和传输零点图,其中输入u=[Φ,δe]T,输出y=[V,γ]T。由图1可知,系统存在一个不稳定极点s=2.47和不稳定传输零点s=4.08,该零点和极点之间频率间隔很小。由于不稳定零点和极点分别构成了控制系统带宽的上限和下限约束,因此控制带宽的设计空间较小。
此外,由图1可知,系统存在三阶弹性模态,其中一阶模态弹性振动频率较低,由于静不稳飞行器需要高带宽控制器来保证稳定性,低阶弹性频率与控制带宽频率相近,控制指令容易激励弹性模态,从而引起结构控制耦合问题。
为了改善系统非最小相位特性和抑制弹性振动,本文研究鸭翼作为冗余舵面,与升降舵进行联动控制。本文假设升降舵大小和安装位置均保持不变,鸭翼的尺寸固定,并与升降舵以增益kec进行联动,其中kec≤0。
当鸭翼以增益kec与升降舵联动控制时,相关的气动系数等效为
(4)
2 鸭翼对非最小相位零点的影响
采用尾舵控制的飞行器,航迹响应均具有非最小相位特性,即传递函数γ/δe有一个不稳定零点。由文献[10]可知,该传递函数的分子可表示为
其中, 1/Tγ3=-1/Tγ2为沿虚轴对称的一正一负的实根,1/Tγ3位于右半平面。
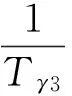
(5)
其中

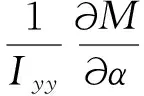

定义瞬时转动中心为lcor=Zδe/Mδe,并代入式(5),有
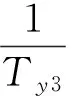
(6)
由此可见,可通过调整lcor来调整不稳定传递函数零点的位置。显然,系数Zα<0,且对于不稳定飞行器来说,Mα>0。零点频率变化趋势如图2所示,当lcor>0时,1/Tγ3为实数,且其频率随lcor减小而增加;当lcor=0,1/Tγ3频率理论上将达到无穷;当Zα/Mα≤lcor<0时,1/Tγ3变成虚数,当lcor=Zα/Mα时,频率为零;lcor 由于lcor由舵面产生的升力和俯仰力矩所决定,采用鸭翼与升降舵联动控制,可通过调整联动增益kec和鸭翼的位置xδe来调节lcor到需要位置,lcor表达式变为 (7) 为了便于分析,令k=-kec·(Zδc/Zδe),此时式(7)变为 (8) 易知式(8)的分母项恒为正。由图2可知,当取k=1时,lcor=0,鸭翼产生的升力刚好抵消升降舵产生的升力,不稳定零点移向无穷远处。当0≤k<1时,lcor>0,零点为不稳定实根,且随着xδe朝向质心后移,鸭翼所产生的力矩变小,从而lcor逐渐变大。当k>1时,lcor<0。如上分析可知,当k=1时,零点的频率可达到最大,从而留给控制系统带宽设计空间最大。 高超声速飞行器细长体外形、轻结构设计导致机体弹性模态频率较低,与控制系统带宽交叠,导致控制指令能够有效激励弹性模态,从而引起弹性失稳。采用鸭翼作为附加的控制舵面,与升降舵进行联动控制,合理选择鸭翼位置和控制增益,则可满足对刚体运动控制的同时避免激励一阶弹性模态。此时,控制舵面产生的广义力为 (9) 代入式(9),得到如下关系式: φ1(xδc) (10) φ1(xδe)-kφ1(xδc)] (11) 由式(11)可知,可通过调整增益k及鸭翼位置xδc来降低舵面指令对一阶弹性模态的激励。 前两节研究了鸭翼对高超飞行器开环系统的影响,下面将结合反馈线性化和LQR理论,针对弹性高超声速飞行器设计鲁棒非线性控制器,在此基础上,研究鸭翼联动控制对飞行器闭环性能的影响,并进行仿真验证。 为了采用反馈线性化方法,将弹性动力学考虑成一种未建模扰动,即不对其直接进行控制,只是通过选择合适的鸭翼配置来避免舵面指令对弹性模态的激励作用。 为了满足相对阶要求,忽略掉控制舵面所产生的升力和阻力项。此外,将发动机系统视为如下二阶动态系统,指令Φc作为新的输入变量: (12) 根据经典的输入输出线性化方法,通过对输出变量求导可以得到: (13) 其中 取控制指令如下式: u=G*-1(v-f*(x)) (14) 将式(14)代入式(13),得到: (15) 至此系统被线性化为2个解耦的伪线性子系统。针对上述伪线性系统,可采用带积分补偿的LQR方法来设计。经过反复尝试,LQR的权值矩阵分别选择为 QV=ding(10,1,1,1),RV=1 Qh=ding(1,10,1,1,1),Rh=0.05 通过经典的LQR求解过程,求解Riccatti方程得到控制矩阵KV、Kh。 定义坐标变换: 其中 伪控指令可写成如下形式: 为了验证本文设计的基于反馈线性化的LQR控制器和鸭翼配置方案的控制效果,对弹性高超声速飞行器的非线性模型进行仿真。在h=25 908m,V=2 347.6m/s状态点处,跟踪100 m/s速度阶跃指令和1000 m的高度阶跃指令,指令均通过如下二阶参考模型进行滤波: (16) 其中,ω=0.039,ζ=0.9,图4给出了参考指令图。 根据第2、3节的分析结果,为了使鸭翼消除非最小相位特性和抑制一阶弹性模态,鸭翼的安装位置选择为满足条件φ1(xδc)=φ1(xδe),联动增益选为k=1。系统采用鸭翼联动控制前后两种情况的非线性仿真对比结果如图5所示。从仿真结果可看出,所设计的控制器能够快速平稳的跟踪速度和高度指令,跟踪误差快速收敛,验证了所设计控制器的正确性和有效性。 可看出,与无鸭翼情况对比,增加合理配置的鸭翼作为额外控制舵面时,消除了系统非最小相位特性,从而减小了控制器设计所用模型与系统真实模型之间的误差,使得系统跟踪误差更小,且收敛速度更快;且经过合理配置,升降舵面与鸭翼对一阶弹性模态的激励力相互抵消,从而避免了控制系统对一阶弹性模态的激励,使得弹性模态响应被大幅削弱,闭环系统高频震荡被有效抑制,系统的稳定性得到增强。 图6给出了控制指令的时间历程。可见,鸭翼与升降舵进行联动时,有效舵效增加,升降所需升降舵偏的指令更小,从而一定程度上可避免舵面饱和的出现,且舵面指令的震荡幅值和震荡时间也得到优化。 然而,除了实际工程中鸭翼所需面临的严峻的气动热问题之外,单纯从控制角度来看,鸭翼也会带来一些消极的影响。从图5可以看出,当采用鸭翼控制时,系统所需配平攻角变大,且增大的幅值较高。经分析,这是由于鸭翼抵消了升降舵产生的升力,使得飞行器整体升力变小,因此需要更大的攻角来达到新的升重平衡。由于高超声速飞行器的需要较大的控制舵面来克服静不稳定特性以及平衡发动机推力产生的抬头力矩,使得舵面产生的升力对总升力贡献很大,因此需要较大的攻角增量来补偿被抵消的这部分升力。进一步分析,由于较大的攻角会产生更大的阻力,因此将需要更大的油门指令来平衡阻力,正如图6所验证。此外,从图5中还可以看出,由于攻角产生的弹性模态广义力也会变大,从而使得飞行器弹性模态的静变形更加显著。这些问题都会给飞行器带来不利的影响,因此实际应用中需要折中考虑各方面的因素。 (1)鸭翼可有效改变不稳定传输零点的频率,从而缓解甚至消除系统严重的非最小相位特性。 (2)调整鸭翼的增益和位置可减弱甚至消除控制指令对一阶弹性模态的激励,从而保证弹性模态的稳定性。 (3)仿真结果表明,经选择合适的联动增益和鸭翼位置,附加鸭翼控制可显著提高闭环系统的稳定性和响应性能。 [1] Bolender M A,Doman D B. A nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle[J] Journal of Spacecraft and Rockets,2007,44(2):374-387. [2] Bolender M A,Doman D B. Flight path angle dynamics of air-breathing hypersonic vehicles[R]. AIAA 2006-6692. [3] 葛东明.临近空间高超声速飞行器鲁棒变增益控制[D]. 哈尔滨:哈尔滨工业大学,2011. [4] Oppenheimer M W,Doman,D B,Bolendern M A,et al. A flexible hypersonic vehicle model developed with piston theory[C] //AIAA Atmospheric Flight Mechanics Conference and Exhibit,Hilton Head.South Carolina,2007. [5] Oppenheimer M W,Skujins T,Doman D B,et al. Canard-Elevon interactions on a hypersonic vehicle[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit.2008,Honolulu,Hwaii. [6] Parker J T,Serrani A,Yurkovich S,et al. Control-oriented modeling of an air-breathing hypersonic vehicle[J] . Journal of Guidance,Control,and Dynamics,2007,30(3): 856-869. [7] David L R,Jackson E B,Buttrill C S. Simulation study of impact of aeroelastic characteristics on flying qualities of a high speed civil transport[R]. NASA/TP-2002-211943. [8] Sigthorsson D O,Jankovsky P,Serrani A,et al. Robust linear output feedback control of an airbreathing hypersonic Vehicle [J] . Journal of Guidance,Control,and Dynamics,2008,31(4) :1052-1066. [9] Fiorentini L. Nonlinear adaptive controller design for airbreathing hypersonic vehicle[D]. Ohio State University,2010. [10] McRuer D T,Ashkenas I,Graham D.Aircraft dynamics and automatic control,Chap.5[M].Princeton University Press,Princeton,NJ,1973:336-337. Nonlinearcontrolofflexiblehypersonicvehicleswithcanard ZHU Jiao1,3,CHEN Wan-chun1,MA Hong-zhong2,YANG Zhi-hong3 (1.School of Astronautics,Beijing University of Aeronautics and Astronautics,Beijing 100191,China;2. UAV Technology Institute,Beijing 100074,China;3. Beijing Aerospace Technology Institute,Beijing 100074,China) For a hypersonic vehicle with unstable longitudinal dynamics, non-minimum phase and severe aeroelastic effects, the design of flight control system is a challenging task. The feasibility of the strategy using canard in conjunction with the elevator as an additional factor is investigated, aiming to eliminating the non-minimum phase behavior and suppress the elastic mode, and to improve the performance of control system. First, a flight dynamic model with flexibility effects is presented. Second, the effects of the placement and relative ganging gain of the canard on the non-minimum phase behavior and elastic modes are demonstrated. At last, with the design of a nonlinear controller based on feedback linearization and LQR technology, the performances of the strategies with and without canards are comparatively evaluated. The simulated results show that, with the placement and relative ganging gain carefully chosen, the proposed control strategy provides an increased level of closed loop performance by suppressing the non-minimum phase behavior and eliminating control excitation of the first elastic mode. hypersonic vehicles; canard; non-minimum phase; elastic modes; feedback linearization; nonlinear control V448 A 1006-2793(2017)05-0660-06 10.7673/j.issn.1006-2793.2017.05.022 (编辑:吕耀辉)

3 鸭翼对弹性模态运动的影响
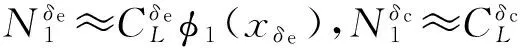

4 带鸭翼的弹性高超声速飞行器非线性控制器设计
4.1 基于反馈线性化的非线性控制器设计
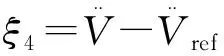
4.2 仿真结果分析
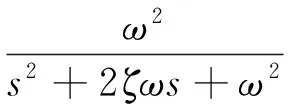
5 结论
