基于数字图像相关法的复合材料结构失效分析

王 朝，常新龙，张有宏，张 磊，陈向东

(火箭军工程大学 动力工程系，西安 710025)

2017-04-17；

2017-06-01。

国家自然科学基金(11302249)。

王朝(1992—)，男，硕士生，研究方向为失效物理与可靠性 。E-mail：2698963107@qq.com

基于数字图像相关法的复合材料结构失效分析

王 朝，常新龙，张有宏，张 磊，陈向东

(火箭军工程大学 动力工程系，西安 710025)

针对纤维增强复合材料失效机理复杂的问题，采用数字图像相关法对拉伸试验中的复合材料表面位移进行数字化处理，建立了基于Hashin改进准则的结构模型，对比试验和仿真结果，分析试件的失效过程和机理。运用蒙特卡洛方法和有限元法，讨论并分析影响结果精度的因素。结果表明，数字图像相关法能够用于观察和分析复合材料结构的失效过程；基于Hashin改进准则的仿真模型与试验结果一致，可以作为进一步细观力学分析的基础；相对于其他结构参数，纵向拉伸强度对结果精度的影响更大。该结果可为复合材料可靠性分析提供理论参考。

数字图像相关法；复合材料；结构模型；可靠性分析；失效

0 引言

复合材料以抗腐蚀性能好、耐热性能优异、比刚度和比强度较高等优点，广泛用于航空、航天领域[1-2]。同时，也因复合材料性能对于制作工艺的依赖性，材料与结构的同一性等特点，导致复合材料失效过程较为复杂，对复合材料的结构设计和可靠性评估造成较大影响。因此，研究纤维增强复合材料的失效过程和失效机理显得尤为重要。

目前，对复合材料结构失效过程的研究，大多采用仿真计算和试验验证相结合的方式[3-5]。景钊等[4]建立寿命预测模型，对复合材料疲劳寿命进行预测，但所采用的样本过少，模型精度有待验证；樊钰等[5]对纤维材料和基体材料的变化规律进行了分析，但是未涉及具体结构的变化。现有的研究对于层合板的具体失效机理涉及较少，尤其是试验过程中的结构变化情况也需要作深入研究，而数字图像相关法(Digital image correlation，简称DIC)作为一种新型的测量方法，能够对结构表面全场位移和应变进行分析，可通过研究试件的应变场变化来分析失效过程。

针对炭纤维复合材料结构的失效过程和失效机理研究，本文采用数字图像相关法(DIC)对复合材料结构进行数字化处理，观测和记录试件拉伸试验过程中的应变云图；分析失效机理，建立基于Hashin改进准则的拉伸试验模型，对照试验结果分析试件的失效过程；基于所建立的模型，运用蒙特卡洛抽样方法研究影响结果精度的因素，为下一步将该方法应用于复合材料结构设计和可靠性分析等更广泛的领域提供参考依据。

1 基本原理

1.1 复合材料基本力学方程

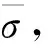
细观应力-应变关系：

σ=C×ε

(1)

式中C为材料刚度矩阵。

宏细观参数的关系：

已有大量工作研究了该方程的求解[6-8]，本文不再对过程进行赘述，只将结果介绍如下：

(2)

式中σ0为宏观应力；R为纤维半径；θ为圆心角；C(β,γ)为宏细观刚度矩阵；Am(β,γ)为与细观几何结构以及子单元材料刚度相关的子矩阵；ε(β,γ)为细观应变矩阵。

1.2 Hashin改进准则

在纤维增强复合材料拉伸试验的过程中，复合材料试件会产生基体破坏、分层和纤维断裂等损伤，现有的仿真计算大多是以Tsai-Hill准则、Tsai-Wu准则等为基础开展的，无法详细分析上述损伤过程，而Hashin准则可以准确表示这些损伤过程。但目前采用的Hashin准则在进行损伤变量计算时，所采用的唯象法无法表征和计算材料分散性，使得整个计算过程的损伤变化不连续。

考虑将参数的威布尔分布引入材料的损伤过程中，损伤过程可以由退化系数表示，由文献[9]可知，在考虑威布尔分布后，其表达式为

(3)

式中m为威布尔分布的形状参数；e为自然对数的底数；ε为拉伸过程中结构的应变；εf为材料的失效应变；Γ为伽马函数。

改进后的Hashin准则如表1所示。

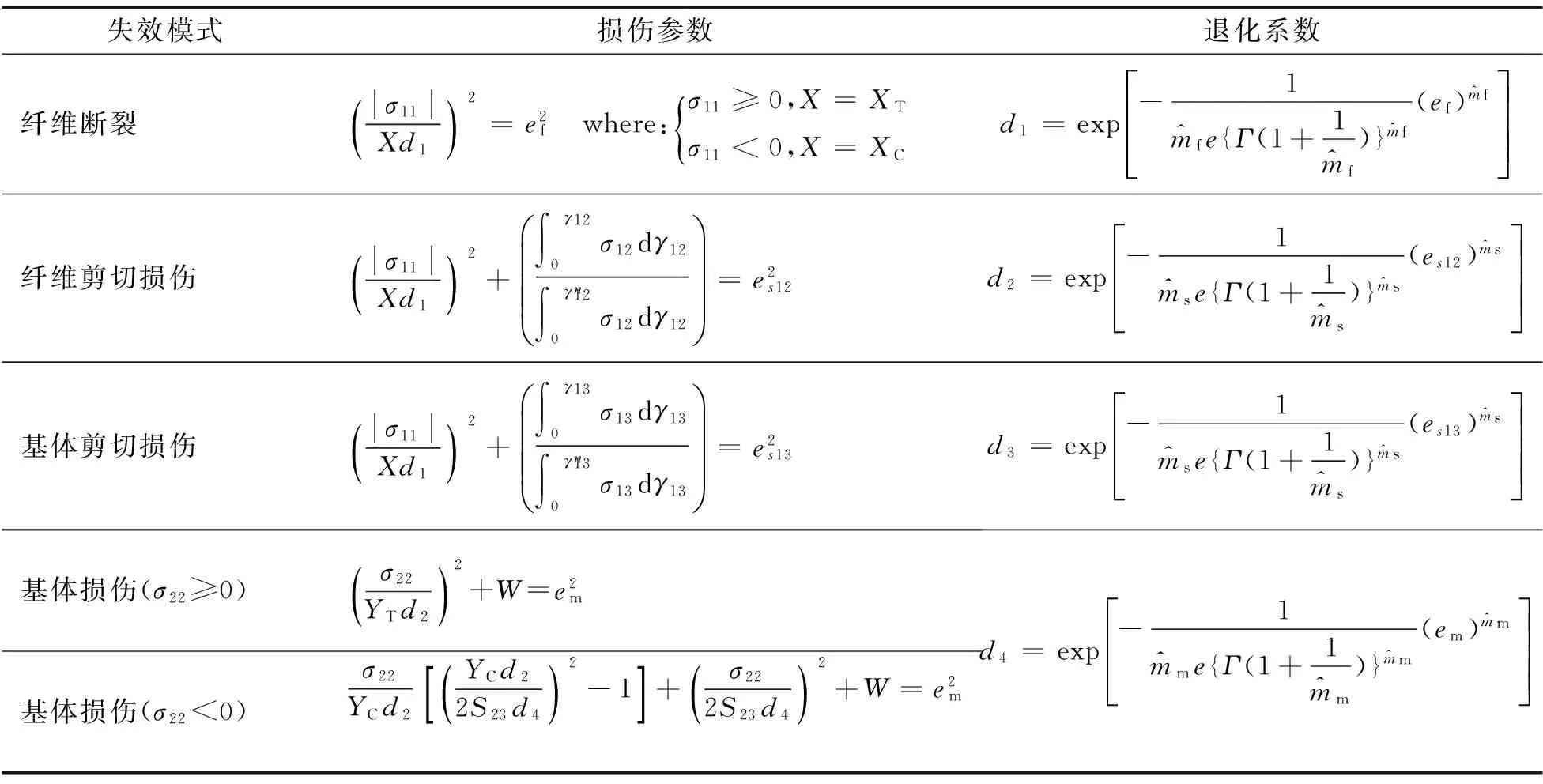
失效模式损伤参数退化系数纤维断裂σ11Xd1()2=e2f where:σ11≥0,X=XTσ11<0,X=XC{d1=exp-1^mfe{Γ(1+1^mf)}^mf(ef)^mféëêêêùûúúú纤维剪切损伤σ11Xd1()2+∫0γ12σ12dγ12∫0γn12σ12dγ12æèçççöø÷÷÷=e2s12d2=exp-1^mse{Γ(1+1^ms)}^ms(es12)^mséëêêêùûúúú基体剪切损伤σ11Xd1()2+∫0γ13σ13dγ13∫0γn13σ13dγ13æèçççöø÷÷÷=e2s13d3=exp-1^mse{Γ(1+1^ms)}^ms(es13)^mséëêêêùûúúú基体损伤(σ22≥0)σ22YTd2()2+W=e2m基体损伤(σ22<0)σ22YCd2YCd22S23d4()2-1[]+σ222S23d4()2+W=e2md4=exp-1^mme{Γ(1+1^mm)}^mm(em)^mméëêêêùûúúú

在以上各式中W计算公式为

(4)

由文献[10]可知，在对失效模式进行计算时，必须考虑耦合作用影响。出于简化模型的考虑，本文认为损伤是不可逆过程。因此，在实际计算过程中，第n+1步的退化系数应取n和n+1步之间的最小值，即

1.3 数字图像相关法

数字图像相关法(Digital Image Correlation，简称DIC)，又称数字散斑相关法(Digital Speckle Correlation Method，简称DSCM)，主要应用于计算机视觉技术领域。

数字图像相关测量技术是图像处理、技术识别和计算机技术结合的产物，通过将物体表面随机分布的斑点作为变形载体，利用相关算法进行图像处理后得到变形信息，研究和分析结构表面在外载荷或其他因素作用下的全场位移和应变。DIC测量系统一般由CCD摄像机、图像采集卡和计算机组成，该系统测量范围广且自动化程度高。

2 复合材料结构试件拉伸试验

2.1 试验设计

试验参考GB/T 3354—2014《定向纤维增强聚合物复合材料拉伸性能试验方法》，采用环氧树脂和T700炭纤维制备试验所用复合材料的试件，由参考文献[10]可知，该材料属性如表2所示，试件尺寸为250 mm×25 mm×2 mm，按照[±62/02/62/0]s的顺序进行铺设。试验时采用环氧树脂铝制加强片，来保证试件端部不受损伤。

采用微机控制电子万能试验机上进行准静态拉伸试验，运用摄像机检测试件表面位移变化。测试系统所用的传感器是CMOS摄像机，应用ARAMIS进行图像后处理，得到应变场和位移场。

2.2 试验结果分析

应用DIC得到试件表面应变场，选取其中一次试验结果进行分析。图1显示了拉伸试验中试件表面应变变化情况。

复合强度参数取值尺度形状复合模量参数取值内聚性能参数取值XT/MPa248021.8E1/GPa123.4t1/MPa32.4XC/MPa951.414.6E2/GPa9.27t2/MPa68.8YT/MPa32.422.6ν120.31t3/MPa68.6YC/MPa137.710.5G12/GPa3.8GⅠC/(N/m)425S12、S13/MPa77.520.0G13/GPa3.8GⅡC/(N/m)1030S23/MPa68.640.0G23/GPa3.2GⅢC/(N/m)1030

由图1(a)可知，试验开始时，试件表面应变率较为均匀，在0.1%左右；在平均应变率达到0.54%时，试件表面62°铺层沿纤维方向产生明显应变率变化，最大应变率接近0.9%，此时发生初次破坏，如图1(b)所示。拉伸试验过程中，试件两端位移最大，由于第一层与第二层铺层角度相反，相对的位移导致两端的层间剪切力最大，在拉伸载荷共同作用下，试件两端位置最先沿着拉伸方向发生基体破坏和轻微纤维断裂破坏。在试件平均应变率达到1.68%时，试件中部的应变率发生明显突变，达到2.2%，此处产生二次破坏。由图1(c)可知，此时试件受力结构主要是0°方向铺层，因此主要失效模式是纤维断裂。±62°铺层在层间作用力下，随着0°铺层形变而发生进一步破坏，二次破坏发生位置在试件中间位置。此后，主要由±62°铺层未断裂的纤维承受外部载荷，但是纤维方向与外部载荷方向并不一致，很快就因断裂而发生结构破坏。应变率达到1.82%时，试件结构破坏较为严重，由图1(d)可看出，纤维完全发生断裂，试件彻底失效。

试件受到破坏时的失效应力统计结果如图2所示。由图2可知，该批样品失效应力分布较为分散，主要位于[1050 MPa，1160 MPa]区间内，平均值是1110 MPa，失效应变分布与应力分布较为一致，主要位于区间[1.72%，1.83%]，平均值是1.78%。由结果可知，应力和应变相关性较好。

3 拉伸试验仿真分析

由于DIC只能处理试件表面应变场，无法将内部结构变化进行数字化处理，所以为了更加细致地分析结构的失效机理，同时与DIC结果形成对比，运用Abaqus软件对拉伸试验进行仿真计算。

3.1 有限元模型的建立

在仿真建模时做如下假设：在结构试件成型前后，纤维和基体的结构形式和力学性能等均不发生明显变化，各层面之间粘接良好，且没有缺陷；在试件受到拉伸载荷作用时仅产生线弹性变化，试件中的残余应力和试验过程中的干扰因素对试验影响忽略不计。

纤维增强复合材料结构试件依据表2赋予材料属性，有限元模型共分12个铺层，采取对称铺层的方式排布，采用Abaqus仿真软件中的cohesive单元模拟试验时试件出现的分层损伤。

3.2 仿真结果分析与研究

对上述有限元模型进行计算，得出复合材料结构试件的参数变化过程。由于DIC主要是处理得到应变云图，为便于对比分析，所有参数均以应变率为自变量。对所得结果进行数据处理后，得出应力-应变曲线、纤维失效和基体失效随应变变化曲线等。

(1)应力-应变曲线分析

对应力-应变曲线进行分析和处理后，其平均曲线如图3实线所示。

由图3可知，层合板结构应力-应变仿真曲线与真实应力-应变曲线相比一致性较好，特别是在应变率小于0.55%时，仿真曲线和试验结果完全重合，应力-应变呈线性关系，此时层合板并未发生明显结构破坏。当应变率为0.55%时，两条曲线斜率均有明显下降，这是由于此处层合板发生拉伸破坏，仿真模型的刚度矩阵和材料细观结构均发生退化。当应变率大于0.55%后，曲线基本走势一致但是未能完全吻合，仿真曲线斜率大于试验曲线。

分析可知，本文所用的刚度退化矩阵是自行设定，与试验过程中材料损伤情况有一定出入，导致曲线结果不完全一致；当应变率大于1.71%时，试件结构损伤严重但仍未完全失效，试验曲线斜率变小，直至应变率大于1.78%时，曲线才呈现明显下降趋势，而在进行仿真计算时，所设定的刚度矩阵在应变率达到1.73%时已完全退化，无法继续计算，曲线呈现下降趋势。虽然试验应变率大于仿真应变，但拉伸试验过程中试件的损伤更复杂，参数退化更严重，因此由仿真计算得到的失效应力1198 MPa大于试验得到的失效应力平均值1103 MPa。

(2)纤维失效与基体失效随应变率变化曲线分析

由于在进行仿真计算时，采用的是对称铺层的方式建立模型，因此对称铺层的纤维失效和基体失效情况完全相同，结果图4所示。Hashin准则的退化系数并不完全表示结构失效情况，但在一定程度上可反应各成分的损伤情况，基于此本文对拉伸试验中各结构变化过程分析如下。

对比图4可知，在试验开始时，0°铺层的破坏方式是纤维断裂， ±62°铺层的破坏方式以基体破坏为主，同时伴有纤维断裂。应变率为0.58%时，±62°铺层的基体开始开裂而后迅速破坏，整体结构产生初次破坏，此后整体结构的拉伸载荷全部由0°铺层承担，其纤维破坏参数增长速率明显加快；应变率达到1.77%时，0°铺层纤维开始破坏而后迅速断裂，结构产生二次破坏，载荷再次由±62°铺层的剩余纤维承受，此后破坏极为迅速；应变率达到1.81%时，结构试件完全失效。整个失效过程与DIC所记录的层合板失效过程较为一致。

由以上分析可知，所建立的模型与试验过程一致性较好，能较为准确地对纤维增强复合材料的失效过程进行分析。

4 精度影响因素分析

在应用DIC进行分析时，精度对于结果分析时的有效性和准确性影响很大，所以有必要研究精度的影响因素。由于DIC是以位移和应变为处理对象，位移和应变越大，结果分析的精度越高。由拉伸试验结果可知，应变与应力相关性较高。因此，本文认为对应力影响越大的因素对结果精度影响也就越大。

由前文结果分析可知，可运用所建立的模型分析细观参数对宏观性能的影响。本文主要对复合材料试件的失效过程进行研究，因此主要讨论试件的失效应力。在拉伸试验中压缩参数对试件结构失效的影响较小，所以在分析参数对性能的影响时，主要讨论纵向拉伸强度XT(纤维方向)、横向拉伸强度YT(垂直于纤维方向)、弹性模量E1和E2以及泊松比ν12。

按照表2所示参数分布，运用蒙特卡洛方法对纵向拉伸强度XT进行采样，运用有限元方法计算失效应力，对结果进行分布拟合，可得如图5所示结果。

由图5可知，采用正态分布和威布尔分布均对统计结果进行描述效果均较为理想。正态分布拟合之后平均值是1188 MPa，方差是36，威布尔分布参数分别是1208 MPa和29 MPa，两种分布拟合与试验结果的平均值1110 MPa较为接近。同理，对横向拉伸强度YT，弹性模量E1、E2和泊松比ν12进行采样后，计算失效应力并拟合其分布，结果如图6～图8所示。

由图6可知，对于横向拉伸强度YT，正态分布平均数是1190 MPa，方差是1，威布尔分布参数分别是1191、1194 MPa，正态分布拟合效果更好。由图7、图8可知，当弹性模量E1、E2和泊松比ν12发生变化时，失效应力变化范围极小，因此不再对其结果分布进行拟合。

综上所述，纵向拉伸强度产生变化时，失效应力分布在[1220 MPa, 1300 MPa]之间，分布较为广泛，当横向拉伸强度产生变化时，失效应力主要在[1188 MPa, 1192 MPa]之间变化，要明显小于纵向拉伸强度的响应范围，说明所有细观参数中纵向拉伸强度对复合材料结构的失效应力影响最大。由以上分析可知，运用本文所制备的试件进行拉伸试验时，纵向拉伸强度XT对结果的精度影响最大。

5 结论

(1)对试件进行拉伸试验，由统计结果可知，该批试件的失效应力分布较为分散，平均值是1110 MPa，失效应变分布与应力分布较为一致，平均值是1.78%。

(2)采用建模仿真结合实验结果，分析了复合材料层合板试件的拉伸失效过程：首先以基体失效为主，而后发生纤维失效，当最大应变大于1.81%时，试件完全失效，所得结论与试验结果较为一致，证明了所建立模型的适用性与准确性。

(3)运用所建立的模型分析影响结果精度的因素，由结果可得，在本文所采用的试件进行拉伸试验时，结构参数对结果精度均会造成影响，其中纵向拉伸强度XT对精度影响最大。

[1] Jeong H K,Shenoi R A. Probabilistic strength analysis of rectangular FRP plates using Monte Carlo simulation[J].Comput. Struct.,2000,76(3):219-235.

[2] 杜善义.先进复合材料与航空航天[J].复合材料学报，2007,24(1):1-12.

[3] Sriramula S,Chryssanthopoulos M K.Quantification of uncertainty modeling in stochastic analysis of FRP composite structures[J].Composites Part A:Appl.Sci.Manuf.,2009,40:1673-1684.

[4] 景钊，孙秦.复合材料多向层压板疲劳寿命预测[J].固体火箭技术,2013,36(2): 237-242.

[5] 樊钰，叶定友，陈汝训.温度影响下炭纤维/环氧树脂复合材料性能预示[J].固体火箭技术,2013,36(6):831-835.

[6] 胡丽娟，张少睿，李大永，等.细观参数对纤维增强金属基复合材料宏细观力学性能的影响[J].上海交通大学学报,2008,42(3):475-479.

[7] Aghdam M M，Dezhsexan A. Micromechanics based analysis of randomly distributed fiber reinforced composites using simplified unit cell model [J].Composite Structures,2005,71:327-332.

[8] Drago A，Pindera M J. Micro-macromechanical analysis of heterogeneous materials: Macroscopically homogeneous vs periodic;microstructures[J].Composites Science and Technology,2007,67(6):1243-1263

[9] 刘万雷,常新龙,张晓军,等．缠绕复合材料壳体低速冲击损伤试验与仿真研究[J].推进技术,2017,38(1):172-178.

[10] Eun-Ho Kim,In Lee. Low-velocity impact and residual burst-pressure analysis of cylindrical composite pressure vessels[J].AIAA Journal,2012,50(10):2180-2193.

Failureanalysisoffiberreinforcedcompositestructuresusingadigitalimagecorrelationmethod

WANG Chao,CHANG Xin-long,ZHANG You-hong,ZHANG Lei,CHEN Xiang-dong

(Department of Power Engineering,Rocket Force University of Engineering,Xi'an 710025,China)

Aiming at the complicated mechanism for the failure problem of fiber reinforced composite,a digital image correlation(DIC) method was used to obtain the evolution of strain field on specimen surface of the laminated sheet tensile test.A structural model was established as well based on improved Hashin criteria.The simulation results were compared with experimental ones to analyze the failure process and mechanism of the specimen.Based on Monte Carlo method and finite element method,the influence of Micro-parameters on the accuracy of the result was discussed and analyzed.The results indicate that the DIC is capable of analyzing and predicting the structural failure process.The established model based on improved Hashin criteria is in good agreement with the experimental results,which can be used as a basis for the further research on micromechanics.Compared with the other structural parameters,longitudinal tensile strength has a greater impact on the accuracy of the results.The results can provide theoretical reference for reliability of the composite materials.

digital image correlation;composite material;structural model;reliability analysis; failure

V258

A

1006-2793(2017)05-0614-06

10.7673/j.issn.1006-2793.2017.05.015

(编辑：吕耀辉)