基于动力总成液阻悬置的参数识别
2017-11-04曾少波曾发林
曾少波,曾发林
(江苏大学 a.汽车工程研究院; b.汽车与交通工程学院, 江苏 镇江 212013)
基于动力总成液阻悬置的参数识别
曾少波a,曾发林b
(江苏大学 a.汽车工程研究院; b.汽车与交通工程学院, 江苏 镇江 212013)
针对直接节流盘式液阻悬置件,通过材料实验确定了液阻悬置中橡胶材料的本构模型,并建立了液阻悬置的结构模型和液体模型。利用液固耦合有限元分析方法对集总参数模型的相关参数进行识别,在阐明了液阻悬置件减振机理的同时,也获得了液阻悬置件的性能参数。此方法对分析液阻悬置件结构参数与等效参数之间的关系十分有效,为液阻悬置件精准的设计开发与结构优化奠定了基础。
悬置件;本构模型;液固耦合;结构参数;等效参数
悬置系统具有控制动力总成与车架相对运动的作用。为使车架与动力总成相互独立且不发生接触,悬置件的选取尤为重要。在通常情况下,悬置件既要把动力总成工作产生的高频小振动加以隔离,防止其传递到车架上毁坏车架,又要把由于地面不平引起的低频大激励迅速衰减,防止此振动传递到动力总成上引起更大的振动[1]。因此,悬置件要在高频时段时体现出较小的刚度与阻尼,在低频时段时体现出较大的刚度与阻尼[2]。此外,悬置系统还应能使动力总成在怠速和熄火过程中具有良好的稳定性,这就要求其具有双向隔振功能[3]。优良的橡胶悬置在一定程度上起到了隔振的效果,但随着汽车速度的提升,因其本身具有刚度大、阻尼不足和高频动态硬化的缺点,难以满足消费者的需求,这就推动了研究人员对更为复杂的液阻悬置进行深入的研究。液阻悬置件是利用了悬置内部液体在液室内流动的复杂的阻尼特性以及金属材料和橡胶材料的刚度特性,解决了普通橡胶悬置刚度大、阻尼不足和高频动态硬化的问题,且能较好地满足悬置系统要求的频变与幅变特性[4]。但是,由于液阻悬置件的结构比较复杂,且内部液体流动特性很难确定,且液阻悬置件的材料参数选取和结构的相关设计对液阻悬置减振性能的影响尤为突出,因此怎样进行参数选取和结构优化以达到更好的减振性能一直是液阻悬置研究的重点和难点。
笔者以直接节流盘式液阻悬置为研究对象,通过有限元软件ANSYS仿真分析,发现液阻悬置结构参数与等效参数存在一定的规律性。建立液阻悬置动态特性有限元模型和集总参数模型,对其进行流固耦合分析,绘制参数识别曲线,以期对结构参数与等效性能参数的关系研究有一定指导作用,从而为下一步优化设计奠定基础。
1 橡胶本构关系及基本理论
橡胶材料在一定应力范围内具有应力与应变之间一一对应关系的特性,因此若研究区域在此范围内,可将橡胶材料近似认为是弹性材料[5]。应变能密度函数用W表示。该材料本构关系可用应变能密度函数进行表示,称为超弹性材料[6]。由于橡胶材料具有上述特性,所以把橡胶材料当作超弹性材料来研究。一般认为橡胶材料是各向同性且不可压缩的超弹性体,可通过应变能密度函数进行表达,其柯西应力张量σ[7]可用式(1)表达。

(1)
其中:I表示单位张量;B表示左Cauchy-Green形变量;p表示不可压缩下的静水压力;Ii表示B的不变量。
2 液阻悬置几何模型
节流盘式液阻悬置的结构剖面如图1所示。液阻悬置主要是由七大部件组成:螺栓、橡胶主簧、限位盘、解耦盘、底膜、节流盘和液压油。悬置件液室可分为3个主要部分:节流盘液室、上液室和下液室。
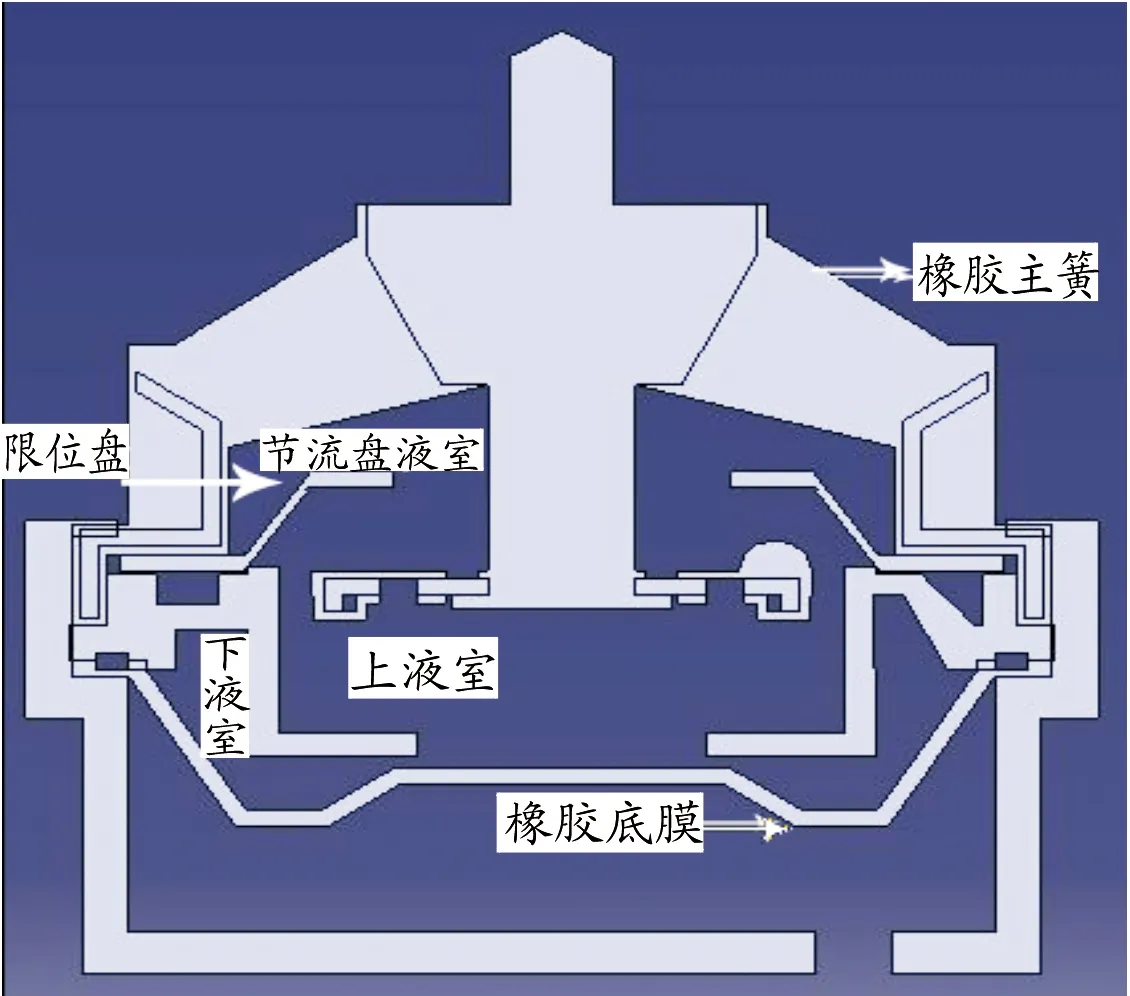
图1 液阻悬置结构
3 液阻悬置集总参数模型
节流盘式液阻悬置件的集总参数模型如图2所示,液室很明显被分成了3份,用Ci、C1和C2分别表示节流盘,上、下液室的体积柔度;kr表示橡胶主簧的动刚度;br表示橡胶主簧阻尼系数;Ap表示主簧等效面积;Ii、Ri分别表示流经惯性通道液体的惯性系数和流量阻力系数;It、Rt分别表示流经节流盘液体的惯性系数和流量阻力系数[8]。

图2 液阻悬置集总参数
动力总成在X(t)的激励下,根据直接节流盘式集总参数模型,可以得到节流盘式液阻悬置的动态方程:
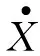
(Am-At)P1
(2)
(3)
(4)
(5)
(6)
在图2所示的集总参数模型中,下液室的体积柔度C2主要由橡胶底膜的尺寸决定。一般液阻悬置的橡胶底膜在2 mm左右,且底膜直接与大气接触,所以C2远远大于C1,一般取C2=C1×103或者K2=0[9]。惯性通道的形状规则,可以直接得到惯性通道的横截面积。设计参数kr、br、Ap、Ri、Rt、Ii、It一般由试验得到或者由近似解析公式计算得到。本文利用非线性有限元分析方法确定这些参数,并确定其与结构参数之间的关系。
4 液阻悬置的有限元模型
由于各个软件存在精度问题,为了减少计算量,把绘制好的三维模型导入ANSYS软件后重新对各个部件的装配进行定义,且运用软件自带的布尔计算得到悬置件内部液体模型,如图3所示。然后再进行网格划分。网格整体选用四面体网格,网格大小适中,液体模型与固体模型的接触面网格大小相近,尽量减少网格扭曲现象,实现计算的快速收敛。此悬置件的结构模型单元数为5 005,液体模型单元数为3 126,如图3所示。固体模型中橡胶主簧和底模的内表面、惯性通道内表面、解耦盘内表面和节流盘表面是液固耦合面;液室内螺栓表面定义为滑移面;液体模型中、上液室和下液室的外表面为液固耦合面。根据实际情况,对每个部件进行材料的赋予,其中节流盘是由自然橡胶与铁块硫化而成。在整个有限元仿真中,铁块认作为刚体。对整个结构模型除橡胶主簧部分表面和底膜下表面以外的表面都进行固定约束。
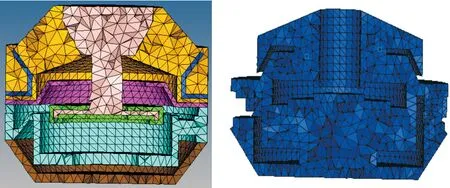
图3 液阻悬置结构与流体模型
4.1 橡胶主簧的刚度
橡胶主簧的静刚度ks与动刚度kr关系:
kr=f·ks
(7)
其中f为相关系数,取值为1.2~1.6。因此,只要获得橡胶主簧的静态刚度就能估算出橡胶主簧的动态刚度[10]。
运用INSTRON单通道伺服系统对悬置件进行静刚度与动刚度测量,装置如图4所示,静刚度曲线如图5所示。由图5可知:静态刚度几乎为恒定值,且为195.6 N/mm。
4.2 橡胶主簧等效面积
橡胶主簧的等效面积为与橡胶主簧发生同样的位移x并排开同样的液体体积Q的面积Ap[11],即
Apx=Q
(8)
橡胶主簧在动力总成因自身重力受到一定的载荷作用,一般不同的预载荷会产生不同的等效面积[12]。橡胶主簧一般由橡胶材料与骨架硫化得到,这样可提高橡胶的刚度,且变形可控制。橡胶材料的超弹性本构模型有多种表达式,表达式中的未知参数一般由材料“应力-应变”试验数据拟合得到。如图6所示,试验类型包括单轴试验、等双轴试验、平面剪切试验和体积试验。将试验数据输入有限元软件中,软件会用最小二乘法进行拟合[13]。对悬置件上的橡胶材料进行相应的试验,得到相应拟合的“应力-应变”曲线,如图7所示。

图4 INSTRON单通道伺服系统试验装置
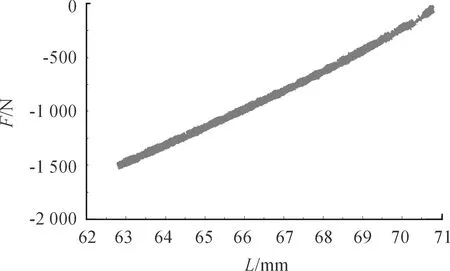
图5 液阻悬置静刚度曲线

图6 橡胶材料拉伸实验
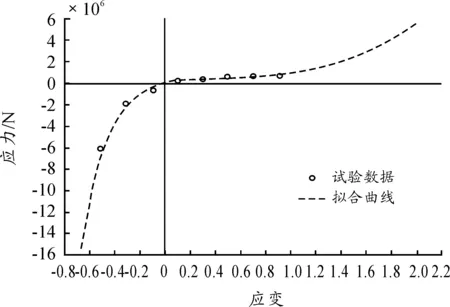
图7 橡胶材料拟合的应力-应变曲线
图8为对橡胶主簧等效面积非线性有限元计算的模型及边界条件。橡胶主簧内骨架、橡胶材料区、上液室液体分别被赋予不同的材料属性。橡胶主簧的内腔与液体相接触的表面定义为液固耦合面,与螺栓接触的液体表面定义为moving wall。橡胶主簧下端与汽车底盘连接,因而设定橡胶主簧下端的边界条件自由度为0,液体下表面定义为 Outlet。在螺栓头上端面施加一沿Z轴方向的位移边界载荷,可得不同位移载荷作用下流经上液室下端面的液体流量,利用式(8)可得出橡胶主簧等效面积与Z轴方向上的位移关系,如图9所示。
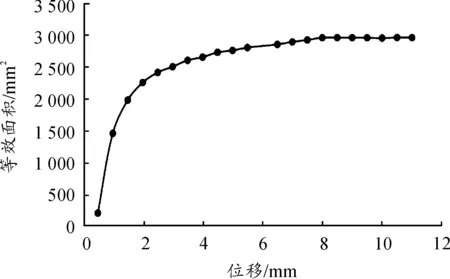
图9 橡胶主簧等效面积曲线
由图9可知:橡胶主簧在预载荷1 200 N的情况下,Z轴方向位移的变化在0.5~3 mm范围内,Ap随位移的增加而增加;在大于3 mm时,等效面积保持稳定在2 500 mm2左右。
4.3惯性通道质量惯性系数和阻力系数
液体流经惯性通道的动量方程为
(9)
傅里叶转换到频域得

(10)
由式(10)可知:在获得悬置件惯性通道两端压力差和在液体流经惯性通道时在频率段所表现出的特性,就可以得到流体流经惯性通道时的惯性系数和阻力系数。
惯性通道中液体外表面和通道内壁相接触,定义为液固耦合面,其结构模型与液体模型如图10、11所示。惯性通道入口端为压力载荷的加载面。对模型进行液固耦合求解分析时,在入口端施加正弦压力载荷,记录出口端流量变化。由式(10)可得液体流经惯性通道时的惯性系数和阻力系数,如图12、图13所示。

图10 惯性通道结构模型

图11 惯性通道液体模型

图12 惯性通道的惯性系数曲线
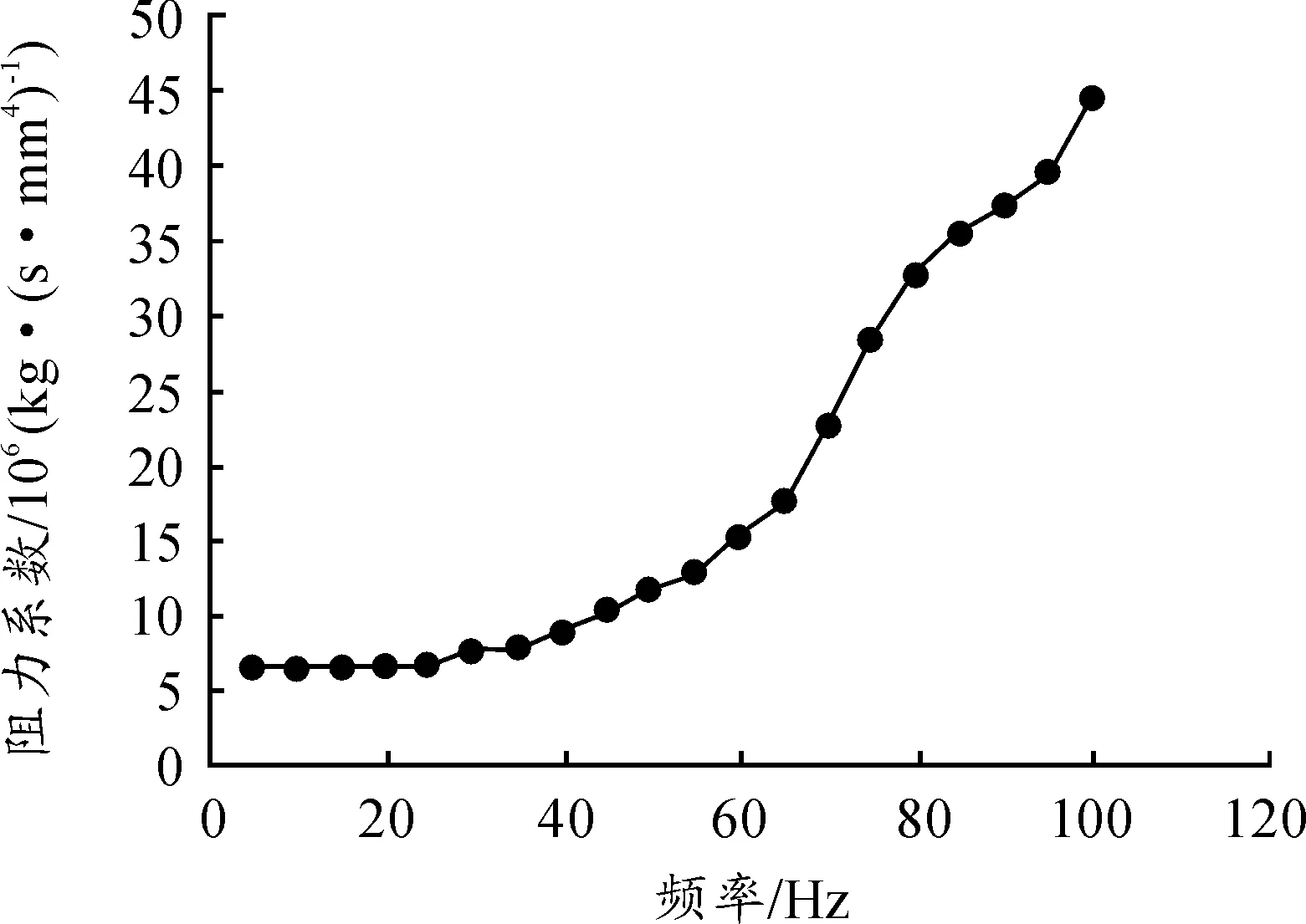
图13 惯性通道流量阻力系数曲线
当惯性通道两端压力差的变化频率较低时,液体流经惯性通道时的惯性系数和阻力系数几乎保持不变;当惯性通道两端口压力之差的变化频率大于38 Hz时,流经惯性通道的液体的质量惯性系数与流量的阻力系数都随着频率的增加而迅速增加,说明高频时惯性通道内的液体惯性大,且受到十分大的阻力,液体几乎不能流动。此时悬置件的阻尼特性主要是液体流经3个液室提供的。在高频时,液体在节流盘上、下液室之间流动关系分析见本文4.4节。在低频时,液体流经惯性通道的惯性系数和流量的阻力系数变化不大。由图12、13可得:在低频、大振幅时,液体流经惯性通道的惯性系数和阻力系数分别为3.154×106kg/m4和 6.366×107N·s/m5。
4.4 节流盘液室体积柔度
节流盘液室体积柔度Ct等于节流盘液室内平均压力与节流盘液室体积变化之比,即

(11)
由式(11)可知:只要知道节流盘液室内平均压力变化和体积变化就可以得到该液室的体积柔度,而这2个参量在液固耦合有限元软件中很容易获得。所以,本文采用有限元法获得了该参数。固体部分有限元模型如图14所示,即橡胶主簧的有限元模型。液体模型如图15所示。之后进行液体-橡胶2种不同材料结构耦合的有限元计算。

图14 节流盘液室结构模型

图15 节流盘液室流体模型
获得的节流盘液室的柔度如图16所示。在0~10 Hz内,节流盘液室柔度极大,即节流盘液室刚度极小,说明在此期间悬置件所承担的载荷几乎都是橡胶主簧所支撑的。在10~15 Hz频段时,节流盘液室柔度迅速减小,体积刚度迅速增大,此时液室产生一定阻尼,并分担一部分载荷;在频率大于15 Hz时,节流盘液室柔度保持不变,值大约在1.47×105mm4/N(即体积刚度为6.8×10-5N/mm4),即在15 Hz以后,节流盘液室内部压力与体积变化为线性。
图17为节流盘液室内的液体阻力系数。由图17可知:节流盘液室内的液体阻力系数随着频率的变化而变化,在0~10 Hz频段内,节流盘液室内液体阻力系数由无穷大迅速降低,在10 Hz时,阻力系数仍然很大。由此可知:在10 Hz以内,节流盘液室里面液体流量很小,几乎为0,从另一方面说明了10 Hz内,悬置所承受的载荷几乎由橡胶主簧来承担,在频率大于10 Hz以后,节流盘液室内部液体的阻力系数迅速降低,最后趋于稳定值,数值大约为1.75×10-5N·s/mm5,说明节流盘液室承担一部分载荷。

图16 节流盘液室柔度曲线

图17 节流盘液室内的阻力系数曲线
4.5 节流盘的惯性系数和阻力系数
节流盘两端压力方程如下:

(12)
同样只要给定节流盘两端液体的压力差ΔP,并确定流过节流盘液体的流量Qi,就可得到节流盘惯性系数、阻力系数。
图18为计算液体流经节流盘的质量惯性系数和流量的阻力系数的结构模型,图19为节流盘的实体模型。由本文4.4节可知,节流盘液室结构模型由橡胶主簧、限位盘以及节流盘上表面橡胶组成,液室的液体模型由流经节流盘上表面与橡胶主簧之间的液体组成。液室内液体与液室内壁的接触面均定义为液-固耦合面。在节流盘上端面上同样压力载荷,记录流经节流盘下端的液体流量。采用式(12)计算可得上液室内液体的惯性系数和阻力系数,如图20、21所示。

图18 节流盘结构模型

图19 节流盘实体模型

图20 节流盘惯性系数曲线

图21 节流盘流量阻力系数曲线
由图20、21可以看出:当节流盘两端压力差的变化频率较低时,液体流经惯性通道时的阻尼系数和阻力系数非常大,即频率低时,液体几乎不流经节流盘液室;当节流盘两端压力差变化频率大于50 Hz 时,液体流经节流盘时的惯性系数和阻力系数几乎保持不变;在频率大于120 Hz时,惯性系数和阻力系数同样保持不变。这就是说明,在高频工况下,节流盘阻挡了液体的流动,消除了高频时出现的硬化现象。因而,在高频、小刚度、小阻尼时,可得液体流经节流盘的惯性系数和阻力系数分别为 3.154×106kg/m4和 6.366×107N·s/m5。
5 结束语
本文主要采用有限元仿真分析方法,对某轿车的直接节流盘式液阻悬置件进行试验测试获得其材料属性。在不同频率、不同振幅下,进行多次施加正弦载荷的非线性有限元仿真分析,从而得到液阻悬置结构参数与等效参数之间的关系。仿真结果也清楚地解释了液阻悬置的实现机理。此外,对节流盘及液室的仿真分析还详细阐述了液阻悬置是怎样解决高频出现的“硬化现象”的。基于液固耦合有限元仿真分析的液阻悬置参数模型动特性分析方法可以在产品的设计开发阶段更准确地预测其动态性能,并进行优化设计、降低开发成本。
[1] ADINA R D.ADINA Theory and Modeling Guide——ADIN-A and F[Z].2001.
[2] 范让林,吕振华,冯振东.惯性通道—解耦板型液阻悬置动特性分析[J].汽车工程,1997,19(4):226-233.
[3] 赵建才,李堑,姚振强,等.车辆动力总成悬置系统的能量法解耦仿真分析[J].上海交通大学学报,2008,42(6):878-881.
[4] 赵建才,李堑,姚振强.橡胶悬置元件结构参数优化设计方法[J].振动与冲击,2008,27(1):16-18.
[5] 张云侠,张建武,上官文斌.新型被动液阻发动机悬置动态特性研究[J].上海交通大学学报,2006,40(6):942-946.
[6] 吕振华,上官文斌.基于液-固耦合有限元仿真的液阻悬置集总参数模型动特性分析[J].机械强度,2004,26(1):29-37.
[7] 龙岩,史文库,骆联盟,等.橡胶主簧的有限元分析及对液阻悬置性能的影响[J].机电工程,2008,25(4):48-51.
[8] 钱若军,董石麟,袁行飞.流固耦合理论研究进展[J].空间结构,2008,14(1):3-15.
[9] 范让林,吕振华,冯振东.惯性通道-解耦膜式液压悬置动特性分析[J].汽车工程,1997,19(4):226-233.
[10] 上官文斌,吕振华.汽车动力总成液阻悬置液-固耦合非线性动力学仿真[J].机械工程学报,2004,40(8):80-85.
[11] 吕振华,梁伟,上官文斌.汽车发动机液阻悬置动特性仿真与实验分析[J].汽车工程,2002,24(2):105-111.
[12] 王伟,邓涛,赵树高,等.橡胶 Mooney-Rivlin模型中材料常数的确定[J].特种橡胶制品,2004,25(4):8-10.
[13] 崔海涛,马海全,温卫东.弹性接触问题的形状优化设计方法[J].应用力学学报,2004,21(2):83-86.
(责任编辑刘 舸)
Parameter-RecognitionBasedonHydraulicEngineMountsofPowertrain
ZENG Shaoboa, ZENG Falinb
(a.Automotive Engineering Research Institute; b.School of Automotive and Traffic Engineering, Jiangsu University, Zhenjiang 212013, China)
Through the study of material testing to determine constitutive model of rubber material included by the hydraulic engine mount, the solid and liquid models on hydraulic engine mount were imported into finite element analysis software to establish a liquid-solid coupling model. It not only clearly explains the relevant mechanisms of reducing vibration, but gets the character of mount. It is effective to study the relationship between structural parameters and equivalent parameters by using this method, which contributes to the precise design development and structural optimizing of hydraulic engine mount.
mount; constitutive model; liquid-solid coupling; structural parameters; equivalent parameters
2016-03-15
江苏省高校自然科学研究项目(11KJA580001)
曾少波(1988—),男,硕士研究生,主要从事振动与噪声研究, E-mail:764143365@qq.com;曾发林(1965—),男,江苏镇江人,副教授,主要从事振动与噪声研究。
曾少波,曾发林.基于动力总成液阻悬置的参数识别[J].重庆理工大学学报(自然科学),2017(10):20-27.
formatZENG Shaobo, ZENG Falin.Parameter-Recognition Based on Hydraulic Engine Mounts of Powertrain[J].Journal of Chongqing University of Technology(Natural Science),2017(10):20-27.
10.3969/j.issn.1674-8425(z).2017.10.004
U463
A
1674-8425(2017)10-0020-08
