轿车座椅R点预测及体压分布研究
2017-11-04张学荣
何 娟,张学荣
(江苏大学 汽车与交通工程学院, 江苏 镇江 212013)
轿车座椅R点预测及体压分布研究
何 娟,张学荣
(江苏大学 汽车与交通工程学院, 江苏 镇江 212013)
以某汽车座椅为研究对象,使用MADYMO软件预测座椅R点,并对体压分布进行研究。基于R点测量的国家标准GB11551—2003《乘坐位置H点和实际靠背角的确定程序》确定R点的预测方法。另外,基于理想体压分布图,采用舒适体压分布特征、最大压力和对称度误差这3个指标来综合评价体压分布的舒适性。在此基础上进行设计参数优化,改变座椅坐垫泡沫刚度进行各种刚度下的仿真计算。计算结果表明:两种预测结果仅相差0.001 m,说明 R点预测方法较准确,具有实际应用价值;座椅泡沫刚度在0.8~0.9倍区间内,可使不同身材的乘员乘坐最舒适。
R点;体压分布;舒适性
汽车座椅的舒适性是整车舒适性的主要因素,座椅设计得不舒适会引起乘员的身体和心理疲劳,增加交通事故发生概率,对生命造成损害[1]。而与座椅乘坐舒适性密切相关的两方面因素是汽车设计之初的座椅R点和乘员落座之后的体压分布[2]。
目前,国内外座椅R点的测量和体压分布的研究一般是通过试验的方法进行的。通过使用坐姿体压分布测量系统、压力传感器垫以及分布式体压分布测试系统等测量方法获得人体的体压分布图。试验通常需要仪器设备、真实座椅、各不同百分位人群和3-DH装置等,并进行大量重复的测试性试验,消耗大量的人力、物力和时间,而且座椅概念设计阶段无法预测其R点及体压分布[3-5]。为此,本文采用MADYMO软件进行座椅R点预测及体压分布的仿真研究,此软件的求解器基于数值模拟方法,可以对座椅乘坐舒适性的长期质量和可靠性进行评估[6]。MADYMO软件还可提供各种不同类型的人体模型[7]。本文通过分别建立3-DH(见图1)装置和座椅模型、95百分位人体和座椅模型来进行R点的仿真预测。由于在以往的研究中人体模型大都使用多刚体模型[3,8],预测结果与人体有较大偏差。本文的人体模型采用facet有限元人体模型,此模型的各个部分尺寸和质量与真人相近,仿真结果更加准确[9]。通过各不同百分位有限元人体和座椅模型的仿真计算得出体压分布图,并进行舒适性评价。

图1 3-DH装置
1 座椅R点预测
查阅R点测量的国家标准GB11551—2003 《乘坐位置H点和实际靠背角的确定程序》,并基于此标准确定R点的预测方法[4]。本文所采用的R点预测方法分别采用2个模型来完成:第95百分位有限元人体和座椅模型(以下简称95百分位模型)、3-DH装置和座椅模型(以下简称3-DH装置模型)。在建模及仿真的基础上,对两种仿真结果进行比较分析。
1.1 R点测量标准(预测依据)
R点是设计时的参考点,也是“座椅参考点”或“乘坐基准点”,是由制造厂为每一乘坐位置规定的设计点,即根据总布置要求确定一个座椅调至最后、最下位置时的设计点,相对于三维坐标系来确定[4]。理论上第95百分位人体的H点应与R点一致。
1.2 座椅R点预测
1.2.1 两种模型的建立
在MADYMO中建立座椅模型。首先,从有限元座椅模型(如图2)中提取节点和单元并导入MADYMO中,建立座椅模型。

图2 有限元座椅模型
其次,从MADYMO中选取95百分位facet人体有限元模型和3-DH装置,分别导入到座椅模型中,并调整人体模型的初始位置和坐姿,定义其与座椅的接触,从而完成两种模型的建立。
1.2.2 座椅泡沫刚度特性材料参数
本文采用改变泡沫刚度比例系数来分析人体与座椅之间体压分布的舒适性,所取泡沫刚度特性曲线(应力-应变曲线)如图3所示。
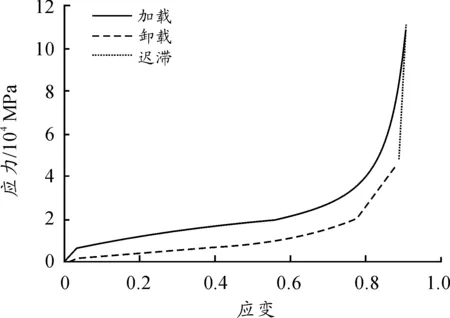
图3 应力-应变曲线
1.2.3 95百分位模型预测结果
95百分位人体模型在重力加速度作用下稳定落座后,其人体H点就是座椅R点。建立的95百分位模型如图4所示。经MADYMO软件仿真计算后,得出其R点预测坐标,如图5所示。

图4 95百分位模型
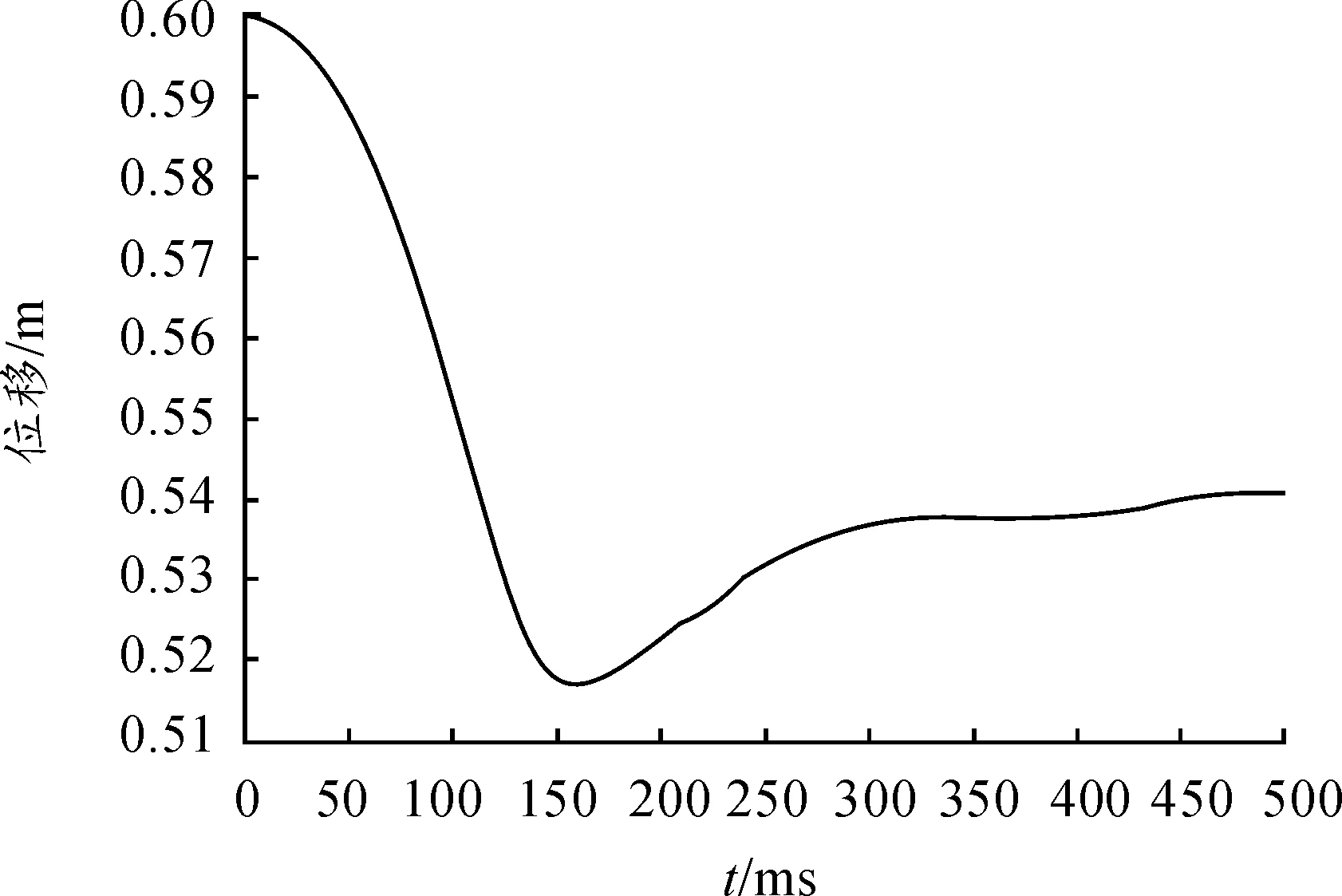
图5 95百分位的R点Z轴坐标
由于人体模型与座椅模型位于同一坐标系,且人体模型只在Z方向上自由下落,因此在水平方向上坐标基本不变,即X、Y坐标值基本不变,重点分析Z轴坐标。
从图5中可以看到:Z轴坐标值开始变化很大,先剧烈下降,后回升一段距离,最后稳定;经过落座稳定后,趋于稳定值0.541 m;在450 ms左右,人体模型与座椅达到平衡。由此预测出座椅R点。
1.2.4 3-DH装置模型预测结果
建立的3-DH装置模型如图6所示。经MADYMO仿真计算,得出的座椅R点坐标,如图7所示。

图6 3-DH装置模型

图7 3-DH装置的R点Z轴坐标
从图7可以看出:Z轴坐标值开始变化很大,先剧烈下降,后逐渐回升,到达平稳值0.543 m时又稍稍下降,最后达到稳定值0.540 m。
对比图5和图7可看出:两者Z轴坐标值变化趋势相同。区别是:图5中Z轴坐标变化幅度更大,且图5中坐标最小值为0.518 m,而图7中Z轴坐标最小值是0.520 m。另外,图5中坐标是平稳回升,最终稳定值为0.541 m,而图7中坐标是先回升后又小幅度下降,最终稳定值为0.540 m。两者相差0.001 m。对比结果如表1所示。

表1 95百分位模型与3-DH装置模型Z轴坐标值对比结果 m
根据表1中数据对比可知: 95百分位模型预测结果略大于3-DH装置模型。
2 体压分布研究
体压分布是指人在稳定落座后,体重作用在坐垫上或者靠背上的压力分布[2-5]。体压分布是座椅乘坐舒适性研究的主要衡量准则,对座椅整体设计也具有指导意义[10]。
建模方法:调用MADYMO中各不同百分位的facet人体模型加入到座椅模型中,定义人体和座椅的初始位置。分别建立出95百分位、50百分位和5百分位的人体座椅模型,如图4、8、9所示。

图8 50百分位模型

图9 5百分位模型
对座椅的坐垫泡沫刚度特性曲线进行放大或缩小,采取的比例因子是0.7、0.8、0.9、1.0、1.1、1.2、1.3。对各个不同比例因子下的模型进行仿真计算,并对仿真结果进行对比分析,得到各不同百分位模型在最舒适体压分布下的泡沫刚度特性曲线。
基于理想坐垫体压分布(如图10所示)可知舒适的体压分布具有如下几个特征:① 人体的大部分质量应以较大的接触面积和较小的单位压力分布在座椅表面;② 压力分布从小到大,无明显突变;③ 压力分布左右对称[2]。

图10 理想坐垫体压分布
为了评价体压分布的舒适性,本文依据舒适体压分布特征、最大压力Pm和对称度误差这3三个指标将舒适度分为4个等级:A为最舒适;B为比较舒适;C为基本舒适;D为不太舒适。
2.1 95百分位理想体压分布研究
对95百分位模型进行变刚度特性分析,经过7次仿真计算,得到7个不同的体压分布图(图11)和体压分布表(表2)。
从图11和表2中可以看出:随着刚度的逐渐变大,人体的体压分布发生着不同的变化,但是体压并没有伴随刚度的递增成正比例递增,而是呈现出先很快减小再增大最后逐渐减小的变化趋势。观察体压分布表可以看出:当刚度比例因子为0.8时,压力分布值最小,舒适度等级最高,最符合理想体压分布,所以座椅泡沫刚度特性曲线在刚度缩小到原来的0.8时可以得到95百分位模型人体最理想的体压分布。
2.2 50百分位理想体压分布研究
同样地,对50百分位模型进行变刚度特性分析,经过7次仿真计算,得到7个不同的体压分布图和体压分布表,如图12和表3所示。
从图12和表3可以看出:随着刚度逐渐增大,人体的体压分布图也在发生着变化,体压伴随刚度的变大逐渐变大,在比例因子为0.9到1.0的刚度变化范围内压力分布变化不大,基本稳定;在此范围外,压力变化较大,舒适度区分较明显。当比例因子为0.9时,压力分布均匀对称,乘坐最舒适,是50百分位模型的最理想体压分布。
2.3 5百分位理想体压分布研究
同样地,对5百分位模型进行变刚度特性分析,经过7次仿真计算,得到7个不同的体压分布图和体压分布表,如图13和表4所示。
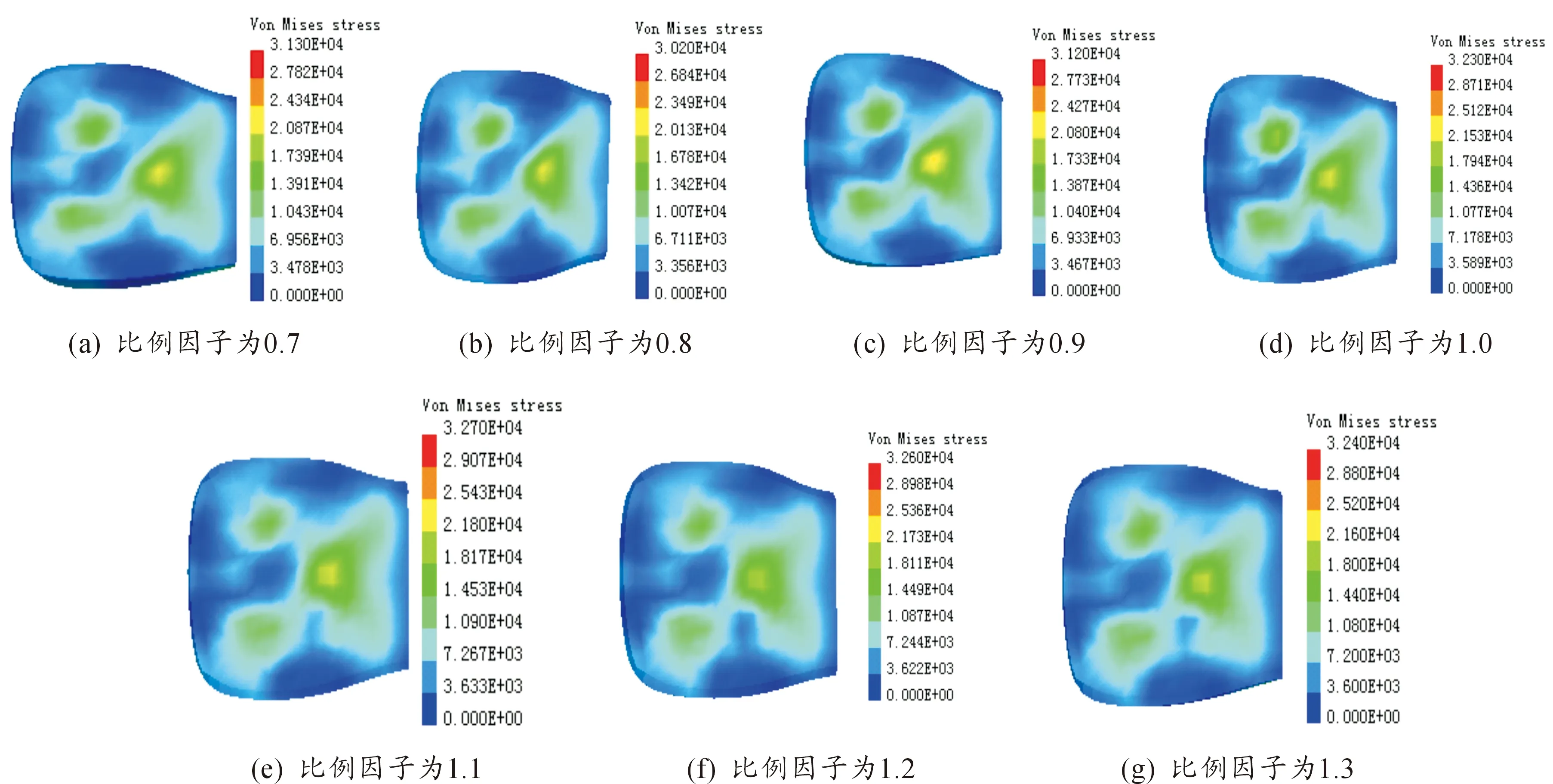
图11 95百分位模型不同泡沫刚度下体压分布

图12 50百分位不同泡沫刚度下体压分布

图13 5百分位不同泡沫刚度下体压分布
表2 95百分位体压分布

刚度比例因子最大压力Pm/kPa左侧大腿压力/kPa右侧大腿压力/kPa对称度误差百分比/%舒适度等级0.731.313.9117.9320C0.830.216.7816.780A0.931.217.3317.330B1.032.314.3621.5333.3C1.132.710.9014.5324.9D1.232.610.8714.4924.8D1.332.410.8014.4025.0D
表3 50百分位模型体压分布

刚度比例因子最大压力Pm/kPa左侧大腿压力/kPa右侧大腿压力/kPa对称度误差百分比/%舒适度等级0.723.212.8015.4716.7D0.824.313.5016.2016.6C0.925.116.7316.730A1.024.916.6016.600B1.125.614.2217.0716.7D1.226.914.9417.9316.6C1.330.613.5610.1725.0D

表4 5百分位体压分布
从图13和表4中可以看出:体压伴随刚度的递增呈现出先减小后增大的变化趋势,在刚度比例因子为0.8时,压力分布最理想,压力值最小,舒适度等级最高;之后压力值逐渐变大。因此,当刚度缩小到0.8倍原刚度时得到5百分位模型的最理想体压分布。
综合分析,此座椅泡沫刚度缩小到0.8倍原刚度时,最适合95百分位和5百分位的人体乘坐;缩小到0.9倍原刚度时,最适合50百分位的人体乘坐。
3 结论
在MADYMO软件中建立95百分位模型和3-DH装置模型,分别仿真计算出座椅R点。对两种R点预测结果进行比较分析,结果表明:两者预测结果仅相差0.001 m,说明本文预测方法较准确,具有实际应用价值,也可用于逆向分析。
本文的创新之处是采用facet有限元人体模型,与以往研究中使用的多刚体人体模型相比,此模型的各个部分尺寸和质量与真人相近,仿真结果更加准确。
经过21次改变泡沫刚度的仿真计算,并依据舒适体压分布特征、最大压力和对称度误差这3个指标来综合评价体压分布的舒适性。最终得出如下结论:此座椅的泡沫刚度缩小至原刚度0.8倍时,最适合95百分位和5百分位的人体乘坐;缩小至原刚度0.9倍时,最适合50百分位的人体乘坐。据此,可知当此座椅泡沫刚度在0.8~0.9倍区间内,可使各不同身材的乘员乘坐最舒适。制造厂可以基于此结论,对座椅刚度进行改变,满足不同百分位人体乘坐舒适性,降低设计成本和时间,加快产品上市进程。
本研究还存在以下方面的局限性:由于在真实环境中人体调查样本的多样性(人体体型等),对于真实人体的调查和试验存在相应的困难。本论文仅依据标准的平均身高及身材的人体模型进行研究,尽可能地模拟大多数的人体,因此相应的真实试验的解决方法及试验步骤还需要进一步研究。
[1] 杜晓明.驾驶员-座椅体压分布模拟研究[D].长春:吉林大学,2012.
[2] 余江鸿.基于体压分布的驾驶员座椅舒适度研究[D].长沙:国防科学技术大学,2008.
[3] 侯件件,张学荣,任利慧.轿车座椅R点及体压分布仿真计算[J].现代交通技术,2011,8(4):65-67.
[4] GB11551—2003,乘用车正面碰撞的乘员保护[S].
[5] KIM S H,PYUN J K,CHOI H Y.Digital human body model for seat comfort simulation [J].International Journal of Automotive Technology,2010,11(2):239-244.
[6] SEOKHEE N.Evaluation of driver’s discomfort and postural change using dynamic body pressure distribution [J].International Journal of Industrial Ergonomics,2005(35):1085-1096.
[7] STEFFEN P.Virtual Simulation of Static and Dynamic Seating Comfort in the Development Process of Automobiles and Automotive Seats[J].Application of Finite-Element-Occupant-Model CASIMIRSAE Paper,2007(1):2459-2463.
[8] BASTIAN M,CHRISTIAN A,MURIELLE V.Virtual Assessment of Seating Comfort with Human Models[J].SAE Paper,2005(1):2678-2682.
[9] MIKE K.Using Failure Mode and Effects Analysis to design a comfortable automotive driver seat [J].Applied Ergonomics,2014(45):1087-1096.
[10] KATRIN M.Simulating Reliability with Respect to Ride Comfort [J].International Journal of Industrial Ergono-mics,2010(24):876-882.
(责任编辑刘 舸)
ResearchonRPointForecastandBodyPressureDistributionofCarSeat
HE Juan, ZHANG Xuerong
(School of Automobile and Traffic Engineering, Jiangsu University, Zhenjiang 212013, China)
Taking a car seat as the research object, the R point is predicted and body pressure distribution is evaluated in this paper based on MADYMO software. By consulting the R point measurement of the national standard GB11551—2003RidePositionHPointsandtheActualAngleoftheBackAngleoftheProgram, the R point of the prediction method is obtained based on this standard. Based on the ideal body pressure distribution map, the comfort of body pressure distribution is evaluated by using the characteristics of the ideal body pressure distribution, the maximum pressure Pm and the symmetry. The calculation results show that, the results of the two prediction only differ by 0.001, and R point prediction method is accurate and has the value of practical application; the seat cushion foam stiffness in the range of 0.8~0.9 times, makes the best comfort of different shape of occupants.
R point; body pressure distribution; ride comfort
2016-10-23
江苏省科技厅企业研究院项目;博士后科学基金资助项目
何娟,女,硕士研究生,主要从事汽车乘坐舒适性研究,E-mail:ab98979695@163.com。
何娟,张学荣.轿车座椅R点预测及体压分布研究[J].重庆理工大学学报(自然科学),2017(10):43-49.
formatHE Juan, ZHANG Xuerong.Research on R Point Forecast and Body Pressure Distribution of Car Seat[J].Journal of Chongqing University of Technology(Natural Science),2017(10):43-49.
10.3969/j.issn.1674-8425(z).2017.10.007
U463
A
1674-8425(2017)10-0043-07
