大客车侧翻稳定性分析及防侧翻鲁棒控制
2017-11-04金智林张甲乐
王 超,金智林,张甲乐
(南京航空航天大学 能源与动力学院, 南京 210016)
大客车侧翻稳定性分析及防侧翻鲁棒控制
王 超,金智林,张甲乐
(南京航空航天大学 能源与动力学院, 南京 210016)
为在大客车不发生侧翻前提下改善客车的操纵稳定性,进行了大客车侧翻稳定性建模分析及主动防侧翻控制研究。考虑乘客变化造成的簧载质量和重心位置变化,以及非簧载质量对大客车侧翻性能的影响,建立线性四自由度大客车侧翻模型。根据汽车侧翻运动规律提出客观评价大客车侧翻稳定性的侧翻因子。在保证大客车不侧翻的约束下,选取防侧翻控制系统鲁棒性及侧倾过程乘客舒适性为博弈双方,设计基于博弈优化的主动防侧翻鲁棒控制策略。通过典型工况侧翻实例分析大客车侧翻稳定性和侧倾时操纵稳定性,以及当前轮转角干扰和乘客数量变化引起参数扰动时的主动防侧翻控制系统的鲁棒性。为降低实车验证的危险性,应用Trucksim软件进行仿真实验,结果表明:该主动防侧翻控制系统可防止大客车侧翻并改善客车操纵稳定性。
大客车侧翻;操纵稳定性;侧翻因子;防侧翻控制;汽车主动安全
大客车侧翻是汽车主动安全领域广泛关注的问题[1-4]。大客车侧翻在交通事故中所占比率不高,但危害是致命的,且作为载客较多的交通工具,大客车的侧翻事故会造成人员“群死群伤”,损失惨重。美国公路交通安全管理局(NHTSA)统计数据表明:2013年美国有568.7万车次交通事故,汽车侧翻事故仅占1.7%,但汽车侧翻伤亡人数占交通事故总伤亡人数的19.1%,且大部分来自客车侧翻事故[5]。我国客车侧翻造成的人员伤亡及财产损失也很大。在2013年全国发生的16起特大交通事故中,与客车侧翻相关的事故占11起,造成158人丧生、147人受伤。因此,对大客车进行侧翻稳定性及防侧翻控制研究是非常必要的。
目前国内外针对SUV及重型汽车侧翻的研究主要包括侧翻稳定性评价[6]及防侧翻控制,而汽车主动防侧翻系统主要应用主动悬架[7]、主动横向稳定器、主动转向[8]和主动制动[9]等作为执行机构,以减小汽车侧倾角、横摆角速度或横向角速度,从而实现防侧翻。为克服单个执行机构的缺点,几种执行机构联合应用成为防侧翻的研究热点。DOUMIATI等[10]联合主动转向及主动制动、SEONGJIN等[11]应用联合主动悬架和主动制动进行了汽车防侧翻研究。重型汽车侧翻系统则相对复杂,需要考虑非簧载质量的影响[12-13]。但针对客车侧翻目前仅关注通过结构强度改进[14]以及对客车结构进行有限元分析及仿真[15-16]来提高客车侧翻的被动安全性能。文献[17]针对充当载客工具的小客车的侧翻稳定性及主动防侧翻技术进行研究,发现乘客数量及分布的变化会影响汽车侧翻稳定性。大客车由于承载旅客多,不仅要考虑乘客数量及分布变化,还需要考虑簧载质量的影响及客车的操纵稳定性等,因此大客车侧翻稳定性与主动防侧翻控制更具理论探索性。
本文以大客车为研究对象,根据汽车侧翻动力学理论建立大客车侧翻模型,按照汽车侧翻运动规律设计了基于博弈论的H2/H∞混合控制器,选取典型侧翻工况进行数值分析,应用Trucksim软件进行大客车防侧翻仿真实验,验证了大客车防侧翻控制方法的有效性。
1 大客车侧翻模型
1.1 整车动力学模型
考虑大客车重心高、非簧载质量大、乘客人数变化大及分布不均等特点,且运动过程中横摆运动、侧向运动及侧倾运动的相互影响、相互耦合的情况,忽略纵向和俯仰方向的动力学特征及前后轴不同特性对大客车侧翻性能的影响,根据达朗贝尔原理建立客车侧翻的线性动力学模型,如图1所示。
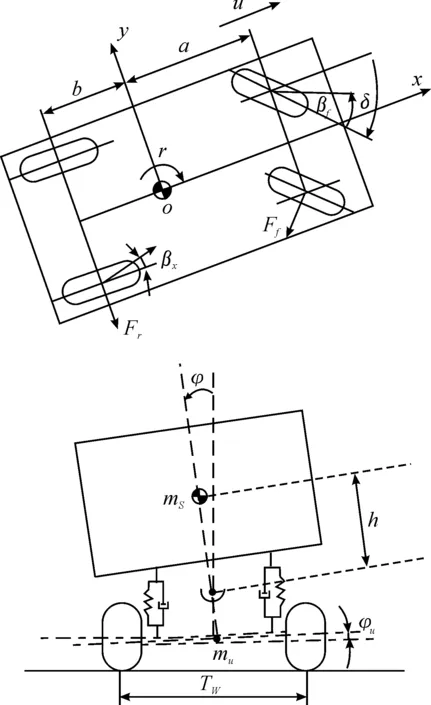
图1 大客车侧翻模型
该模型包括4个运动方向的自由度,其中侧向运动微分方程为
(1)
横摆运动方程为
(2)
簧载质量的侧倾运动方程为
(3)
非簧载质量的侧倾运动方程为
(2Ff+2Fr)hr+mu(hu-hr)ay=
Kuφu-mug(hu-hr)φu-
(4)
客车质心位置横向加速度为
(5)
式(1)~(5)中:m为整车质量;ms为簧载质量;mu为非簧载质量;h为侧倾臂长,即侧倾中心到簧载质量质心距离;hr为侧倾中心高度;hu为非簧载质量质心高度;Ff和Fr分别为前、后轮的侧向力;Ix为簧载质量绕x轴的转动惯量;Iz为横摆转动惯量;a和b分别为客车重心到前后轴的距离;Ks和Ds为悬架的等效侧倾刚度和等效侧倾阻尼系数;Ku为轴向等效侧倾刚度;r为横摆角速度;φ为簧载质量侧倾角;φu为非簧载质量侧倾角;v为横向速度;Mz为抗横摆力矩。
1.2 轮胎动力学模型
轮胎与地面接触的侧向力是提供客车转向的动力,也是影响客车侧翻的作用力,其中前后轮的侧偏角及侧偏力为:
βf=(v+ar)/u-δ
(6)
βr=(v-br)/u
(7)
Ff=-kfβf
(8)
Fr=-krβr
(9)
式中:δ为前轮转角;kf、kr分别为前/后轮侧偏刚度。
1.3 系统状态空间模型
(10)
式中:
将式(10)进行线性变化后得到客车侧翻动力学模型的状态空间方程
(11)
其中:
2 防侧翻控制策略
2.1 客车侧翻因子
横向载荷转移率为左右车轮垂直载荷之差与总垂直载荷的比值,因其侧翻阈值的绝对值固定为1,适合各种车型,所以成为常用侧翻评价指标,但大客车行驶时左右车轮垂直载荷不易直接测量。由图1的力矩平衡方程可得客车左右车轮垂直载荷FL与FR的差值满足关系:
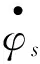
(12)
式中Tw为大客车的轮距宽度。由式(3)(12)及横向载荷转移率的定义可得客车侧翻因子
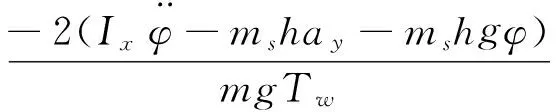
(13)
2.2 博弈H2/H∞控制
将博弈的思想引入汽车主动悬架[18]及防侧翻控制[19]已获得很好应用。大客车行驶工况非常复杂,包括车载乘客变化大、行驶路况复杂多变、侧向风干扰等。主动防侧翻控制策略不仅要保障汽车紧急工况下行驶的侧翻稳定性,还要在客车不发生侧翻时改善汽车侧倾过程的操纵稳定性和主动防侧翻控制系统的抗干扰鲁棒性。因此,以汽车侧翻稳定性为约束条件,选择系统的鲁棒稳定性和客车的操纵稳定性作为博弈双方,设计一种混合H2/H∞鲁棒控制器,控制框图如图2所示,控制流程见图3。
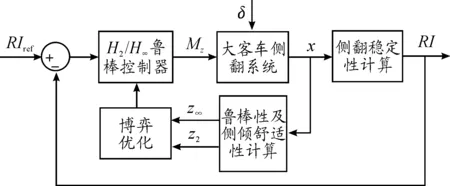
图2 大客车防侧翻控制框图
由汽车侧翻状态空间方程(11)可求出性能评价输出z∞和z2:
z∞=C1x+D1Mz
(14)
z2=C2x+D2Mz
(15)
其中:z∞反映主动防侧翻控制系统的鲁棒稳定性;z2反映大客车的侧倾过程客车操纵稳定性。加权矩阵C1和C2为对角方阵:
其中:qij>0(i=1,2;j=1,2,3,4,5);r1/r2为加权系数。
主动防侧翻的博弈H2/H∞控制流程如图3所示。令
(16)
由式(16)可构造博弈双方的赢得矩阵为
(17)
式中:P1、Q1为保证大客车侧翻控制系统的鲁棒稳定性最优时P和Q的值;P2、Q2为在大客车侧翻控制系统的鲁棒稳定性满足一定条件下,保证最优操纵稳定性时P和Q的值;P3、Q3为在操纵稳定性满足一定条件时保证大客车侧翻控制系统的鲁棒稳定性最优时P和Q的值;P4、Q4为保证操纵稳定性最优时P和Q的值。
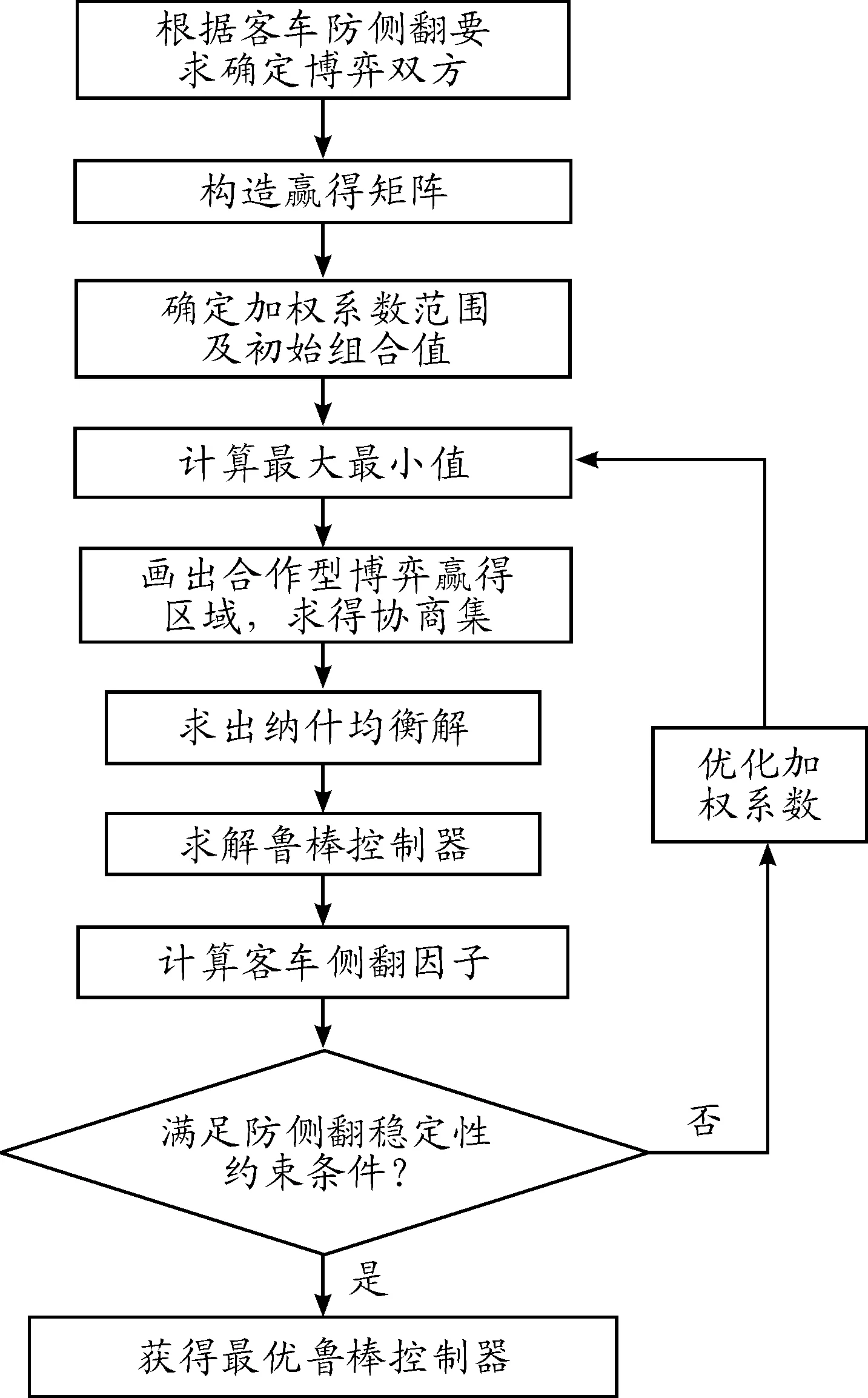
图3 博弈H2/H∞控制流程
由赢得矩阵(17)可得大客车侧翻控制系统的鲁棒稳定性和动态性能的最大最小值为

(18)

(19)
运用纳什均衡求解方法,求出选定加权系数组合下的最优鲁棒控制器,并根据大客车侧翻因子优选加权系数。
3 典型工况数值分析
以某大客车为对象,选取2种典型侧翻工况的前轮转角输入,即J-Turn工况和Worst-Case工况。设置初始车速为100 km/h。表1为某大客车结构及行驶的基本参数。
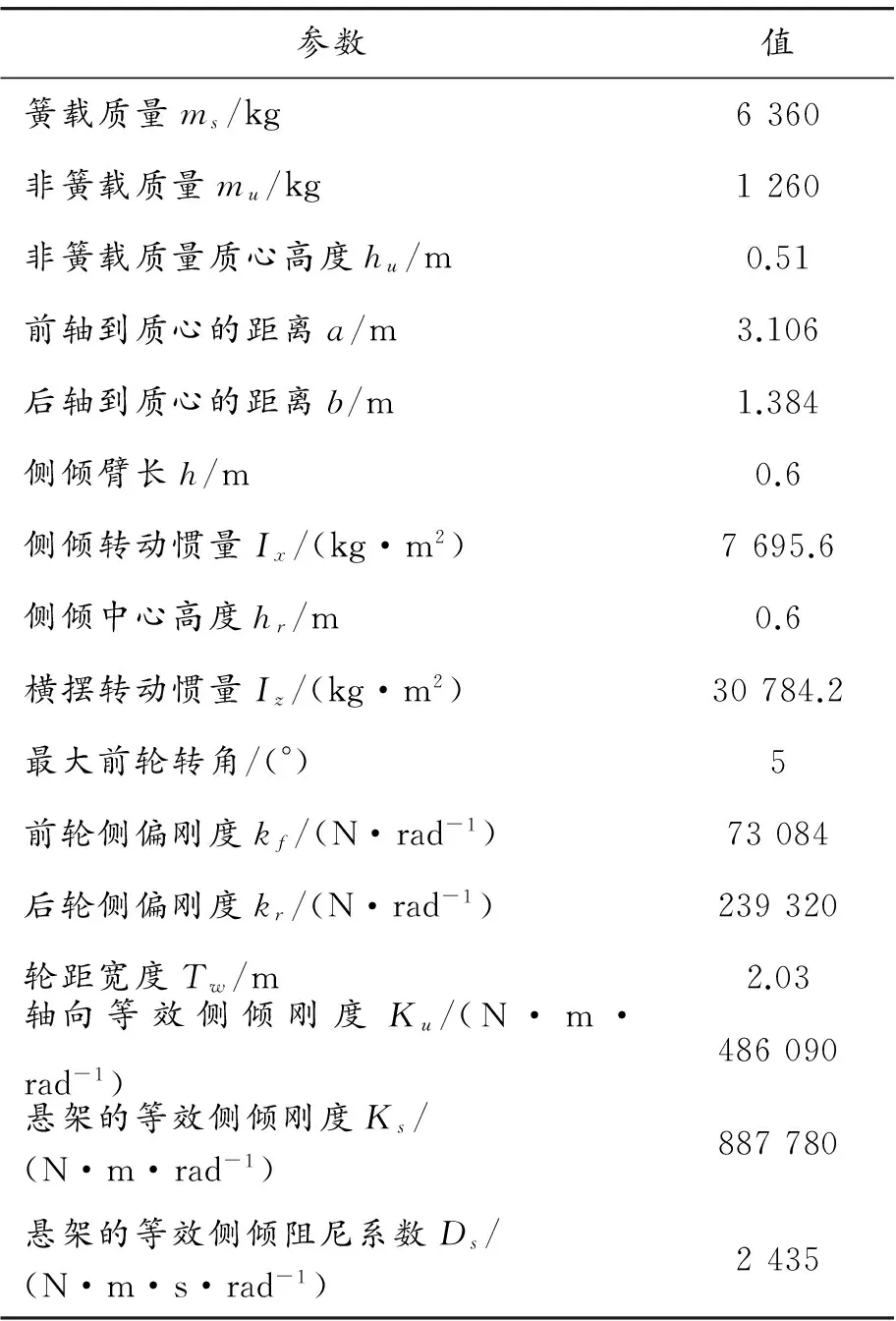
表1 某大客车参数
3.1 侧翻稳定性
分别应用传统H2/H∞鲁棒控制及博弈H2/H∞控制策略对客车侧翻性能进行数值分析,并与未控制的侧翻因子进行对比,结果如图4、5所示。可以看出:2种工况下博弈H2/H∞控制以及传统鲁棒控制方法均能有效防止大客车侧翻,保障了客车侧翻稳定性;相对传统鲁棒控制方法,博弈H2/H∞控制方法减小了侧翻因子最大值和稳态值,缩短了稳定时间,降低了大客车侧翻危险。
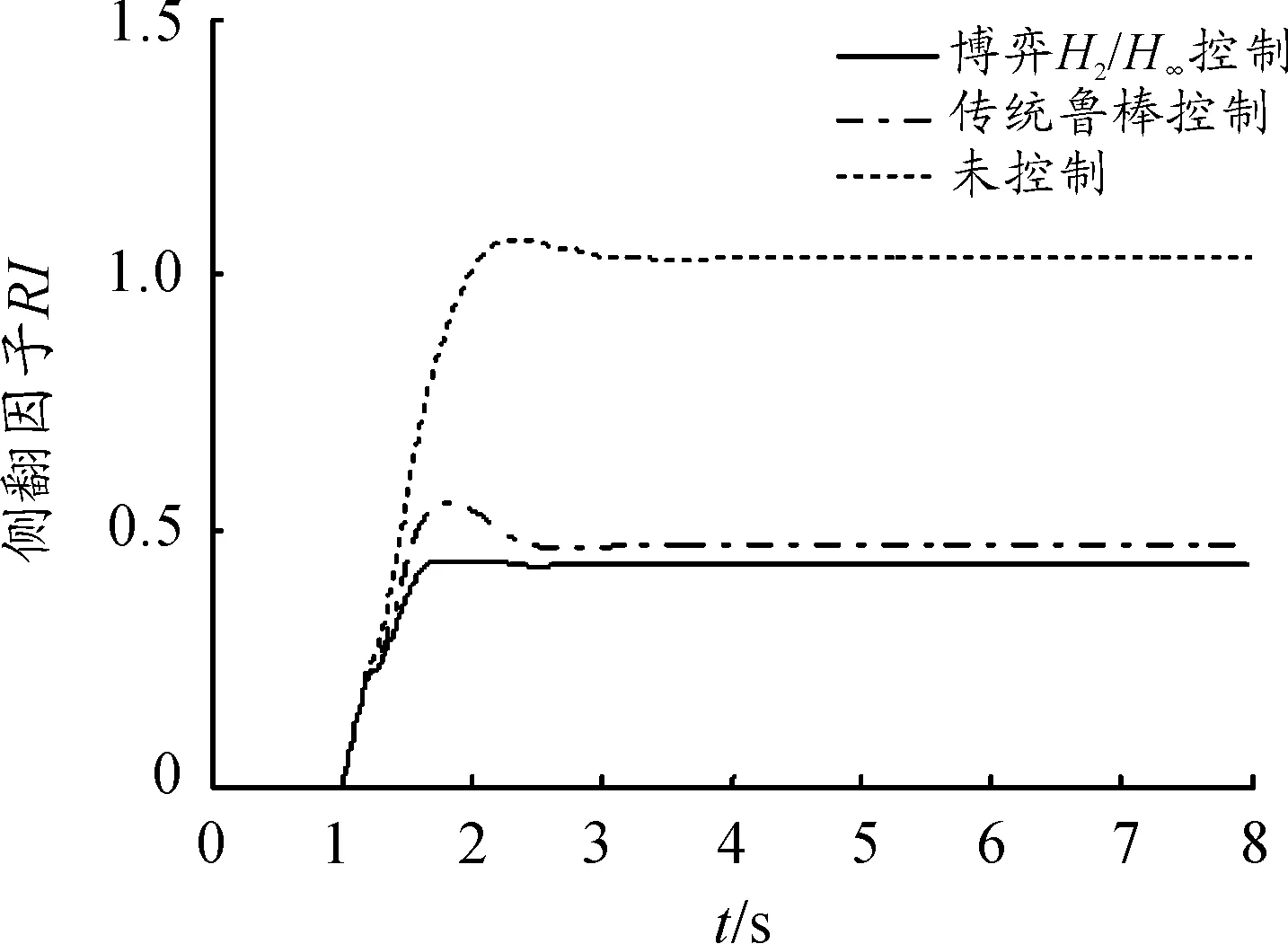
图4 J-Turn工况客车侧翻性能
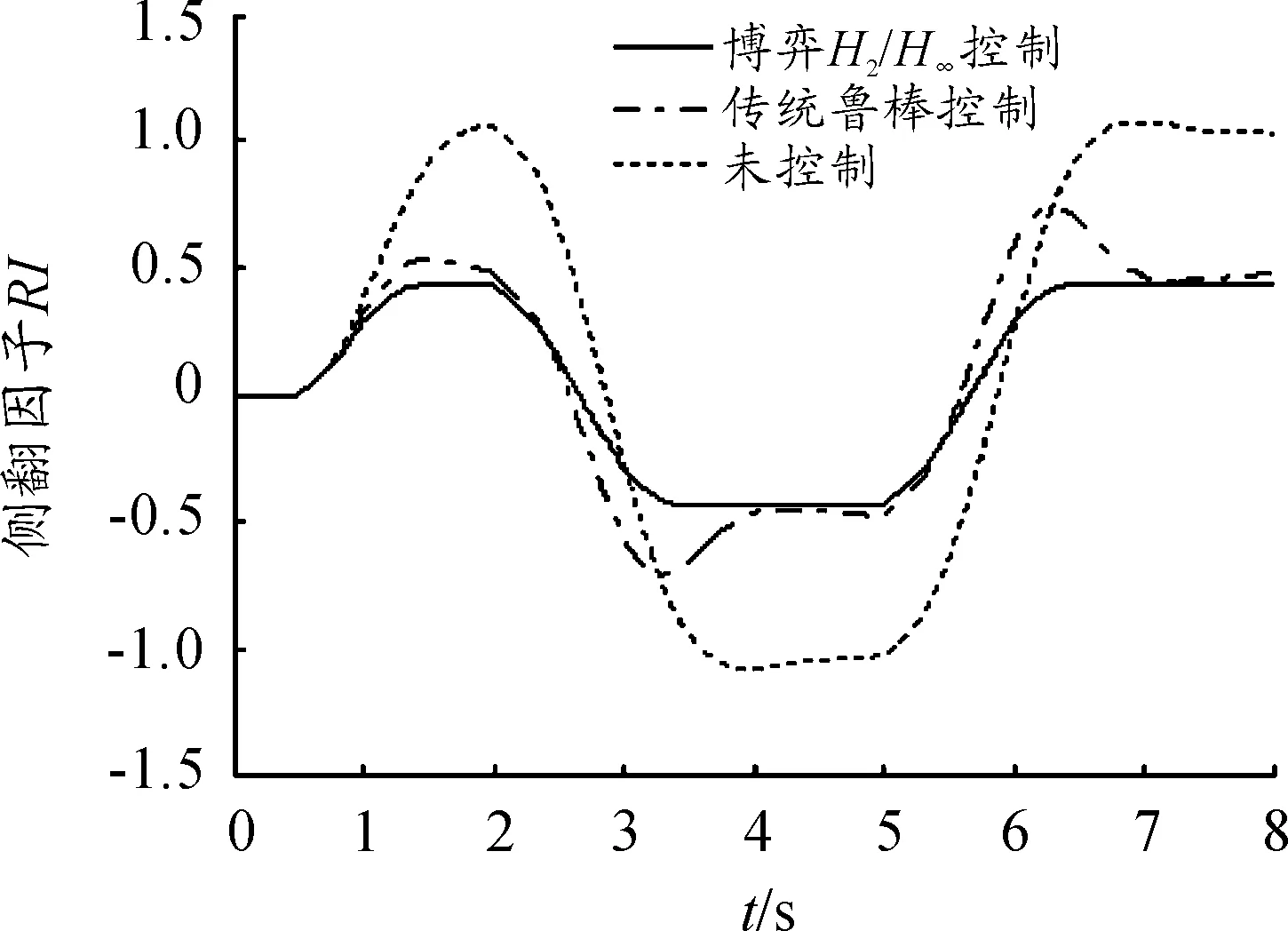
图5 Worst-Case工况客车侧翻性能
3.2 操纵稳定性
为分析客车侧翻稳定的前提下的客车操纵稳定性,选择J-Turn工况的前轮转角输入获得客车侧倾时侧倾角、侧倾角速度、侧向加速度及横摆角速度的响应曲线,如图6所示。
由图6可以看出:相比于传统鲁棒控制方法,博弈H2/H∞控制方法能有效降低客车行驶过程侧向加速度、侧倾角及侧倾角速度的最大值和稳态值,缩短了稳定时间,减少了震荡次数。该方法在保障汽车侧翻稳定性的前提下可有效改善客车侧倾时的操纵稳定性。

图6 客车侧倾响应曲线
3.3 鲁棒稳定性
客车行驶时的主要干扰有前轮转角干扰及参数变化引起的扰动。图7为前轮转角干扰的客车侧倾角与侧倾角速度的相平面图。可以看出:相平面图从原点出发,干扰去除后很快收敛到原点,且侧倾角及侧倾角速度值均在安全范围内。这表明在前轮转角干扰下传统鲁棒控制方法和博弈H2/H∞控制方法均具有良好的鲁棒稳定性。
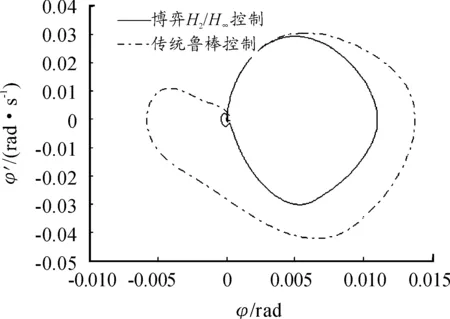
图7 前轮转角干扰下相平面图
客车空载和满载以及乘客分布不均匀时,客车的簧载质量、重心位置等参数会发生变化。图8为客车侧翻因子最大值随簧载质量变化的关系曲线。可以看出:乘客数量增加时侧翻因子最大值均有所减小,且随着乘客数量变化侧翻因子最大值变化很小。表明2种控制策略均在满载时具有更好的防侧翻效果,且在乘客数量变化时具有一定鲁棒性。

图8 侧翻因子最大值与簧载质量关系
图9为重心高度变化时客车侧翻因子最大值变化曲线。可以看出:随着侧倾臂长增大(重心高度增加)客车侧翻因子最大值增大,且2条曲线斜率相近。表明2种控制策略在侧倾臂长参数扰动下具有一定鲁棒性,即博弈H2/H∞控制降低了客车侧翻危险且保持了侧倾臂长参数扰动下的鲁棒性。
图10为重心纵向位置变化时客车侧翻因子最大值变化曲线。可以看出:相对传统的鲁棒控制方法,应用博弈H2/H∞控制策略时客车侧翻因子最大值随重心纵向位置变化曲线平缓。表明博弈H2/H∞控制策略不仅能降低客车侧翻危险,且明显改善了主动防侧翻控制系统在重心纵向位置参数扰动时的鲁棒性。
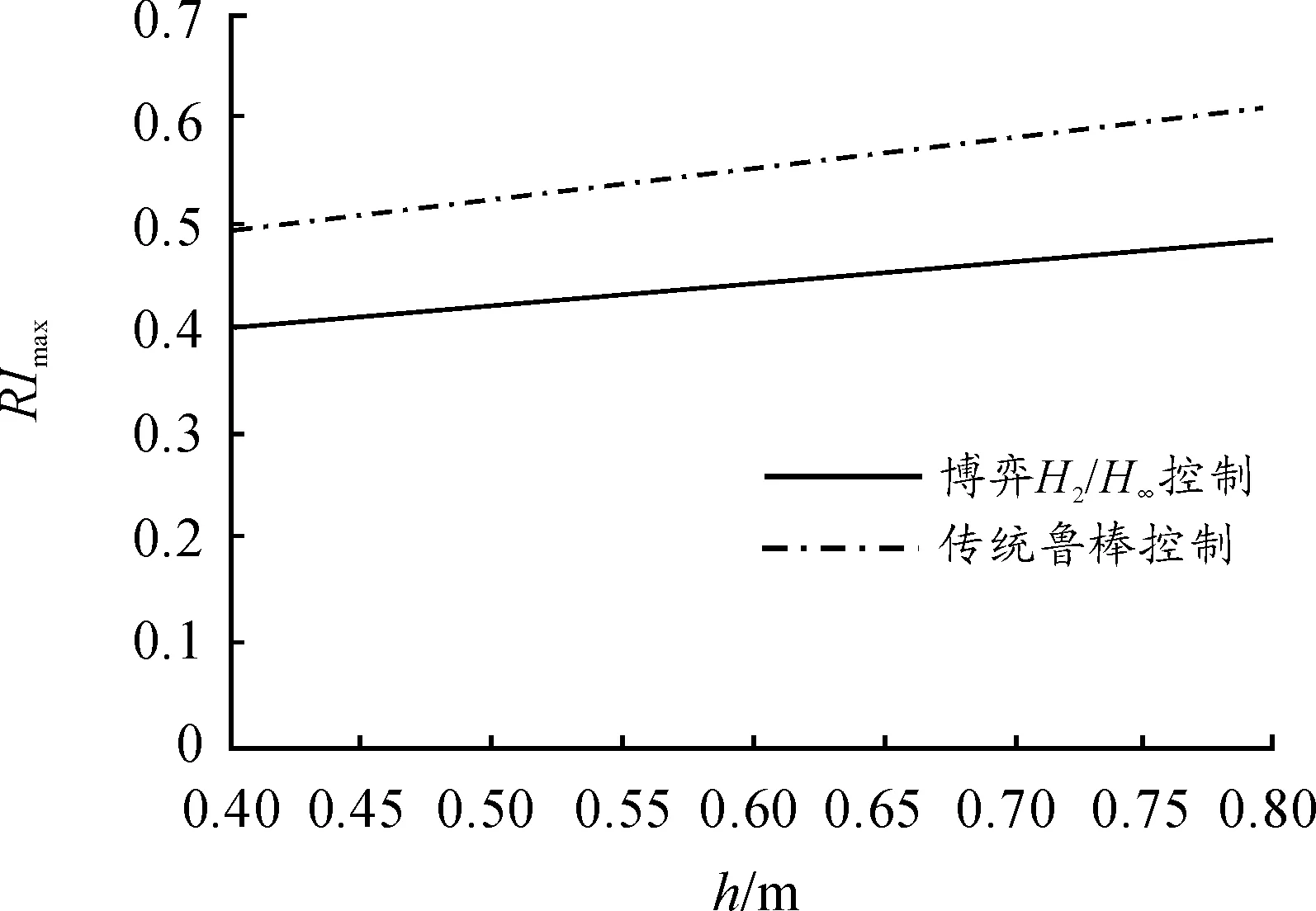
图9 侧翻因子最大值与侧倾臂长度关系

图10 侧翻因子最大值与重心纵向位置关系
4 仿真实验
Trucksim仿真实验不仅可降低客车侧翻实验的危险性和成本,且因其结果更具可靠性而得到广泛认可。为验证大客车侧翻模型的正确性及采用博弈H2/H∞控制方法后的客车防侧翻效果,应用Trucksim进行接近大客车实际运行工况的仿真实验。图11和图12为不同工况下数值分析与仿真实验的结果对比。
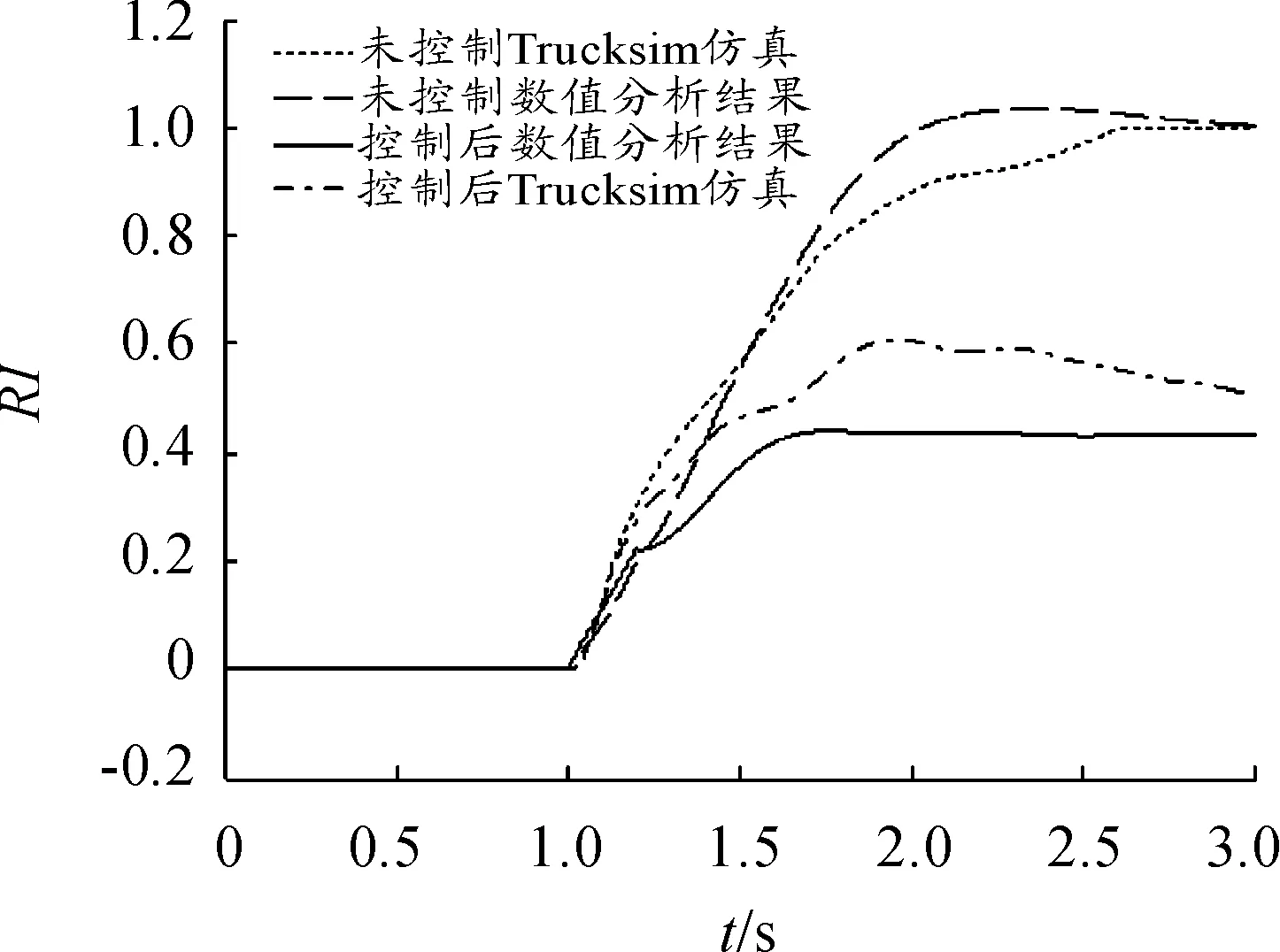
图11 J-Turn工况数值分析与仿真实验结果

图12 Worst-Case工况数值分析与仿真实验结果
由图11可看出:由于仿真实验考虑了非线性轮胎及车身阻尼等实际因素,未控制时数值分析结果及仿真实验结果有所差别,但侧翻趋势一致,均在2.5 s左右客车侧翻因子值达到1,发生侧翻危险。从图11和图12可看出:相对于理想的数值分析,仿真实验防侧翻控制效果略差,但客车侧翻趋势一致,且不同工况下应用博弈H2/H∞控制策略均能防止客车侧翻。
5 结论
1) 建立的侧翻模型简单且能反映大客车的侧翻运动规律。
2) 博弈H2/H∞防侧翻控制策略可在保障客车侧翻稳定性前提下改善客车的操纵稳定性。
3) 博弈H2/H∞防侧翻控制策略可在保障客车侧翻稳定性前提下改善控制系统的抗干扰及参数扰动鲁棒性。
[1] 郝海舟,符志.某客车侧翻的计算机模拟测试[J].客车技术与研究,2015(1):23-25.
[2] 张雷,金智林,赵曰贺,等.基于ADAMS的汽车侧翻稳定性仿真分析[J].重庆理工大学学报(自然科学),2015,29(10):24-28.
[3] 周德生.客车侧翻生存空间仿真评价方法研究[J].客车技术与研究,2015(1):10-13.
[4] 邵毅明,司红建,查官飞.大客车侧翻安全性仿真分析[J].重庆理工大学学报(自然科学),2013,27(2):6-12.
[5] National Highway Traffic Safety Administration,Traffic safety facts 2013:a Compilation of Motor Vehicle Crash Data from the Fatality Analysis Reporting System and the General Estimates System [R].Washington:US,Department of Transportation,DC,2015: 77-85.
[6] DAHMANI H,CHADLI M,RABHI A,et al.Detection of impending vehicle rollover with road bank angle consideration using a robust fuzzy observer [J].International Journal of Automation and Computing,2015,12(1):93-101.
[7] PARIDA N,RAHA S,RAMANI A.Rollover-Preventive Force Synthesis at Active Suspensions in a Vehicle Performing a Severe Maneuver With Wheels Lifted Off [J].IEEE Transactions on Intelligent Transportation Systems,2014,15(6):2583-2594.
[8] SOLMAZ S,CORLESS M,SHORTEN R.A methodology for the design of robust rollover prevention controllers for automotive vehicles with active steering [J].International Journal of Control,2007,80(11):1763-1779.
[9] CHIU J,CORLESS M,SOLMAZ S,et al.A Methodology for the Design of Robust Rollover Prevention Controllers for Automotive Vehicles Using Differential Braking [J].International Journal of Vehicle Autonomous Systems,2010,8(2/3/4):146-170.
[10] DOUMIATI M,SENAME O, DUGARD L,et al.Integrated vehicle dynamics control via coordination of active front steering and rear braking [J].European Journal of Control,2013,19(2):121-143.
[11] YIM Seongjin.Design of a robust controller for rollover prevention with active suspension and differential braking [J].Journal of Mechanical Science and Technology,2012,26(1):213-222.
[12] IMINE H,BENALLEGUE A,MADANI T,et al.Rollover risk prediction of heavy vehicle using high-order sliding-mode observer experimental results [J].IEEE Transactions on Vehicular Technology,2014,63(6):2533-2543.
[13] 朱天军,宗长富,李飞,等.基于线性矩阵不等式的重型车辆防侧翻鲁棒控制算法研究[J].汽车工程,2012,34(5):394-398.
[14] KANG K,CHUN H,PARK J,et al.Design of a composite roll bar for the improvement of bus rollover crashworthiness [J].Composites Part B:Engineering,2012,43(4):1705-1713.
[15] SU Ruiyi,GUI Liangjin,FAN Zijie.Multi-objective optimization for bus body with strength and rollover safety constraints based on surrogate models [J].Struct Multidisc Optim,2011,44(2):431-441.
[16] LIANG C,LE G.Analysis of bus rollover protection under Legislated standards using LS-DYNA software simulation techniques [J].International Journal of Automotive Technology,2010,11(4):495-506.
[17] 金智林,张甲乐,马翠贞.多种群遗传优化的客车防侧翻鲁棒控制方法[J].机械工程学报,2014,50(24):130-136.
[18] 史明光,陈无畏.基于博弈论的H2/H∞混合控制及其在汽车主动悬架中的应用[J].控制理论与应用,2005,22(6):882-888.
[19] TAMADDONIA S,TAHERIB S,AHMADIANA M.Optimal preview game theory approach to vehicle stability controller design [J].Vehicle System Dynamics,2011,49(12):1967-1979.
(责任编辑刘 舸)
AnalysisofRollStabilityandRobustControlofRolloverPreventionforaBus
WANG Chao, JIN Zhilin, ZHANG Jiale
(College of Energy and Power Engineering, Nanjing University of Aeronautics & Astronautics, Nanjing 210016, China)
Bus rollover is a serious traffic accident. To obtain rollover stability and improve the handling stability caused by vehicle rolling, the rollover stability and anti-roll control strategy of a bus are studied. Taking the unsprung mass and the number of passengers variation into consideration, a linear four degrees of freedom model is established to describe vehicle motions, including lateral, yaw and roll motion of the sprung and unsprung mass. From the law of vehicle rollover dynamics, a rollover index is put forward to evaluate the rollover performance of the bus. Also, the game theory and the theory of Nash equilibrium are applied to design a robust control strategy. Furthermore, the rollover stability,the handling stability of the bus, and the robustness of the anti-roll control system are analyzed by typical numerical cases. And the theoretical results are verified by the Trucksim simulation experiment. The results show that the robust control strategy can prevent bus rollover with good dynamic performance and robust stability.
bus rollover; handling stability; rollover index; anti-roll control; vehicle active safety
2017-02-24
江苏省普通高校专业学位研究生实践创新计划项目(SJLX16_0098)
王超(1992—),男,硕士研究生,主要从事汽车安全技术研究,E-mail:atop1290@126.com; 通讯作者 金智林(1978—),男,江西人,博士后,副教授,主要从事汽车安全技术研究,E-mail:7513363@qq.com。
王超,金智林,张甲乐.大客车侧翻稳定性分析及防侧翻鲁棒控制[J].重庆理工大学学报(自然科学),2017(10):12-19.
formatWANG Chao, JIN Zhilin, ZHANG Jiale.Analysis of Roll Stability and Robust Control of Rollover Prevention for a Bus[J].Journal of Chongqing University of Technology(Natural Science),2017(10):12-19.
10.3969/j.issn.1674-8425(z).2017.10.003
U461
A
1674-8425(2017)10-0012-08
