基于双闭环滑模结构的自动泊车路径跟踪控制

江浩斌，沈峥楠，马世典

(江苏大学 a.汽车与交通工程学院； b.汽车工程研究院， 江苏 镇江 212013)

基于双闭环滑模结构的自动泊车路径跟踪控制

江浩斌a，沈峥楠a，马世典b

(江苏大学 a.汽车与交通工程学院； b.汽车工程研究院， 江苏 镇江 212013)

为提高自动泊车系统倒车入库时的路径跟踪控制精度，保证在狭小停车场地情况下自动泊入目标车位的成功率，提出一种双闭环的滑模变结构路径跟踪控制方法。将车辆运动学模型的跟踪控制器系统转换成含有位置控制器和姿态控制器的双闭环级联子系统，并设计一种指数和幂次相结合的趋近律，使泊车跟踪路径在有限时间内达到快速收敛。基于Matlab/Simulink搭建了跟踪控制模型。仿真结果表明：设计的路径跟踪控制算法能保证跟踪点快速收敛到理想路径，可提高自动泊车入库的成功率。

自动泊车；路径跟踪；滑模控制

城市汽车保有量的快速增长致使城市中的停车位资源日益紧张，停车位的空间也越来越狭小。更复杂的停车位场景使驾驶员需要花更多的时间寻找可用停车位，而在泊车入位时由于驾驶员视野存在盲区使得汽车轻微刮蹭、碰撞的事故也越来越多，因而自动泊车系统受到了人们广泛的关注[1]。自动泊车系统是一种不需要驾驶员人工干预，能依靠自身环境传感器识别周围环境并自动停车入位的系统。该系统的出现有助于提高城市泊车入位的成功率和安全性，同时解放驾驶员的双手，降低驾驶员泊车过程中的心理压力，提高驾驶舒适性[2-3]。自动泊车路径跟踪控制作为自动泊车系统的一项关键技术，主要应用于倒车入库过程中，使车辆能够准确按照规划路径行驶，并到达最终停车位置，解决了狭小泊车位场景下驾驶员泊车困难的问题。对规划路径的精确跟踪是评价自动泊车系统性能的主要指标之一[4-6]。

为了提高泊车路径跟踪的精确性，国内外科研和工程技术人员进行了诸多研究。文献[7] 提出一种基于非光滑控制的自动泊车路径跟踪控制策略，通过对车辆动力学跟踪误差模型的降阶转换，推导了2阶、3阶子系统的级联系统有限时间跟踪控制方程。文献[8-10] 以四轮驱动机器人为实验平台,建立了四轮驱动运动学模型，分别基于控制算法设计了不同的路径跟踪控制器。文献[11]基于阿克曼转角建立了车辆前轮转向运动学模型，并提出了3步泊车控制算法，其中：第1阶段为直线路径跟踪；第2阶段为方向角跟踪；第3阶段为停车位置中心跟踪。文献[12]设计了一种理想航向角偏差生成器和基于PID 反馈控制组成的路径跟踪横向控制系统。

显然，现阶段对于自动泊车路径跟踪的研究方法较多，但多数研究的控制算法复杂，存在诸多限制，在实际应用中的路径跟踪效果并不理想。本文从工程应用的角度出发，为降低控制算法的复杂性，实现跟踪点快速收敛，基于车辆动力学模型设计了基于双闭环滑模变结构的自动泊车路径跟踪控制算法，并通过Matlab/Simulink仿真分析验证了所设计算法的有效性。

1 自动泊车工作原理

自动泊车系统由环境感知模块、决策模块、执行模块、通信模块4个部分组成。带有自动泊车系统的整车架构如图1所示。在环境感知模块中，超声波雷达用于探测车位纵深长度，里程计用于探测车位的水平长度。在决策模块中，泊车控制器主要进行数据处理，做出下一步的决策和命令。在执行模块中，EPS(电动助力转向系统)用于控制前轮转向，ESP(车身稳定系统)用于制动，动力模块提供驱动力。在通信模块中，车身CAN用于实现泊车控制器与前述模块的通信。

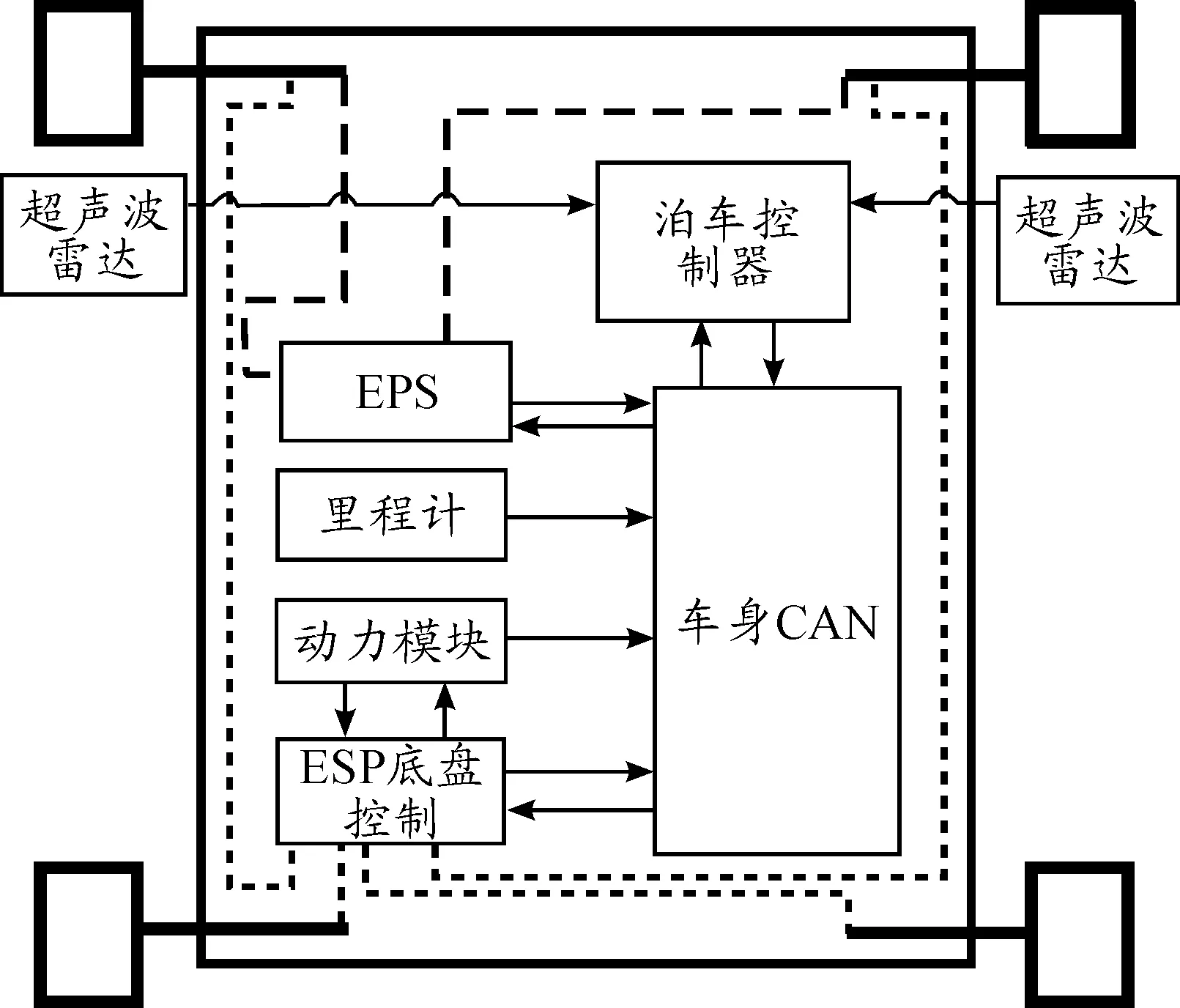
图1 自动泊车系统结构组成

以平行泊车为例，自动泊车的入库过程场景如图2所示。车辆Ⅰ在寻找车位过程中，由起始位置A开始按行驶方向移动，到达位置B时，测距模块完成对空车位的参数扫描；确认空车位后，自动泊车控制器根据车位参数规划出一条理想倒车入库路径，考虑车位的几何约束，一般将平行泊车的理想路径划分为三段式路径。如图2所示，在三段式路径中：第1段为基于最小转弯半径的圆弧线；第2段为直线；第3段为基于最小转弯半径的圆弧线。第2段直线分别与第1段圆弧线和第3段圆弧线相切。规划完路径后，泊车控制器根据路径跟踪控制算法实时控制车速和转向，倒车入库，由位置B最终到达停车位置C[13-14]。

图2 自动泊车入库示意图

2 整车运动学模型

考虑车辆执行器的系统响应速度、控制精度的限制，本文将整车的运动学模型简化为四轮机器人模型，以车辆的后悬架几何中点位置K点为研究对象，建立如图3所示的整车运动学模型。在运动学模型中，车辆的运动状态由坐标系中后悬架几何中点K的位置坐标[x,y]以及车辆航向角α来表示[15]。此外，由于在整个自动泊车入库过程中，车辆的最高车速不高于8 km/h，因而本文忽略车辆转向过程中的轮胎侧滑力影响。

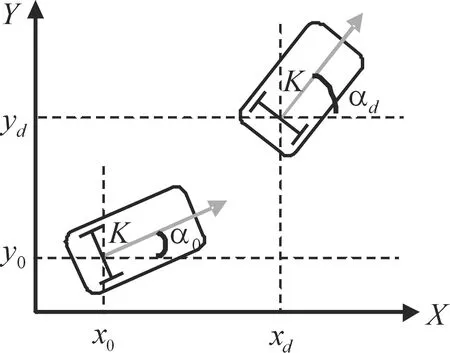
图3 整车运动学模型

自动泊车过程中的运动学方程可表示为

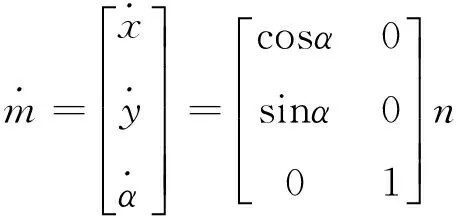
(1)

由运动学方程可得自动泊车车辆的运动学模型为

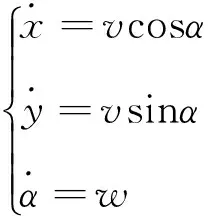
(2)

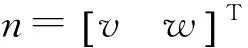
3 基于双闭环滑模结构的运动路径跟踪控制器设计

3.1控制器闭环系统设计

在实践中，控制器采用越复杂的控制算法，其计算量就越大，时效性也越差。由于自动泊车倒车入库需要在窄区域内实现理想路径的精确跟踪，因而对时效性的要求很高，通常需要在70 ms的系统周期内完成1次上层决策的规划。本文从工程应用的角度出发，为降低控制算法的复杂性，将运动学模型(2)的跟踪控制器系统转换成含有位置控制器和姿态控制器的双闭环级联子系统。如图4所示。其中：内环为姿态子系统，外环为位置子系统，内环接收到外环产生的指令信号αd后，通过滑模控制律实现对αd的跟踪，其中αd指理想航向角。

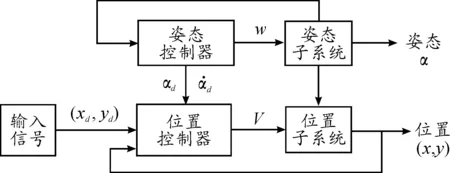
图4 控制器闭环系统结构

3.2 位置控制器设计

位置子系统控制器主要通过控制车辆的车速v实现倒车入库过程中实时位置[x,y]对理想轨迹点[xd,yd]的跟踪。误差跟踪方程为：

(3)

(4)

其中：xe=x-xd；ye=y-yd。

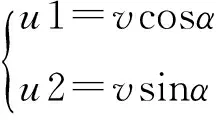
(5)

针对式(3)，取滑模函数s1=xe，则

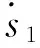
设计控制律为

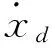
(6)

其中，k1>0。

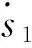
针对式(4)，取滑模函数s2=ye，则

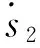
设计控制律为

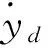
(7)

其中，k2>0。

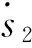
由式(5)可得：tanα=u2/u1。如果α的值域为(-π/2,π/2)，则可得路径跟踪的理想轨迹跟踪角为α=arctan(u2/u1)。

式(5)中所得α为位置控制律所要求达到的航向角，在α和αd一致的情况下，才可实现理想轨迹的跟踪控制，但实际上α和αd在控制的初始阶段不可能完全相等，容易造成控制器闭环系统的不稳定。因而，需将式(5)得到的α当成理想值，即取

αd=arctan(u2/u1)

(10)

因而，可得实际的位置控制律为

v=u1/cosαd

(11)

3.3 姿态控制器设计

由上述分析可知：在控制的初始阶段，实际航向角α和理想航向角αd的偏差会造成闭环系统的不稳定，需要通过设计姿态子控制器使α尽快跟踪到αd。

令αe=α-αd，αe为角度偏差值，取滑模函数为s3=αe，则

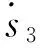
(12)

相比传统的指数趋近控制律

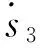
(13)

本文设计了一种指数和幂次相结合的趋近律，

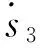
(14)

其中ε、a、k3为正设计参数且满足0<ε<1、a>1、k3>0。相比控制律(13)，控制律(14)中的k3|s|a项保证：在远离滑模面时，趋近速度较大，在滑模面附近时k3|s|a项较小，从而减小抖振。

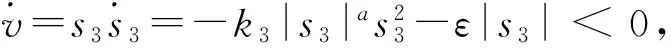
综上，姿态控制律为

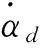
(15)

4 路径跟踪仿真

如图5所示，就上述基于双闭环的滑模控制律，在 Matlab/Simulink 仿真平台上搭建自动泊车路径跟踪控制器模型进行仿真研究。为验证跟踪误差收敛的效果，结合自动泊车入库轨迹特性，针对圆弧路径、直线路径、三段式自动泊车路径分别作路径跟踪仿真实验。针对式(6)(7)(15)，控制律参数取k1=0.3，k2=0.3，k3=4，a=5。控制器闭环系统结构见图5。

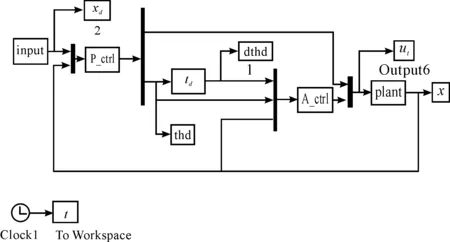
图5 控制器闭环系统结构

4.1 圆弧路径跟踪控制

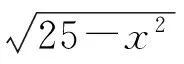
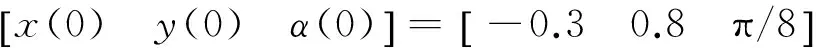
圆弧路径跟踪控制仿真结果如图6、7所示。图6中:圆弧路径跟踪在跟踪起点处就开始快速收敛，在x<0.4 m内，跟踪误差已经收敛为0；x≥0.4 m后，跟踪点已经开始跟踪期望的圆轨迹，且跟踪轨迹具有较好的平滑性。图7中：整个跟踪过程中车速均未超过5 km/h，满足自动泊车最高车速不高于8 km/h的要求。

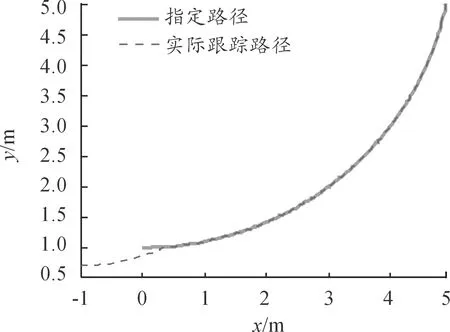
图6 圆弧路径跟踪

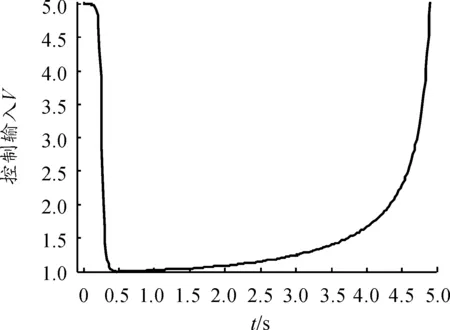
图7 圆弧跟踪速度V输出曲线

4.2 直线路径跟踪控制

指定直线路径y=x+1，x∈[0,5]，仿真中车辆初始位置及姿态取：

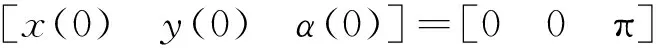
直线路径跟踪控制仿真结果如图8、9所示。图8中：直线路径跟踪点跟踪误差渐进稳定，最终在x<0.3 m内收敛为0，系统在有限时间内到达并跟踪期望的直线轨迹，且跟踪轨迹具有较好的平滑性。图9中：整个跟踪过程中车速均未超过5 km/h，满足自动泊车最高车速不高于8 km/h的要求。

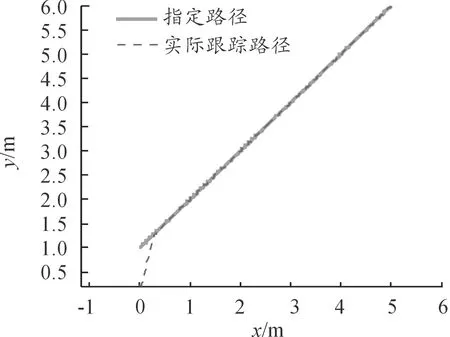
图8 直线路径跟踪

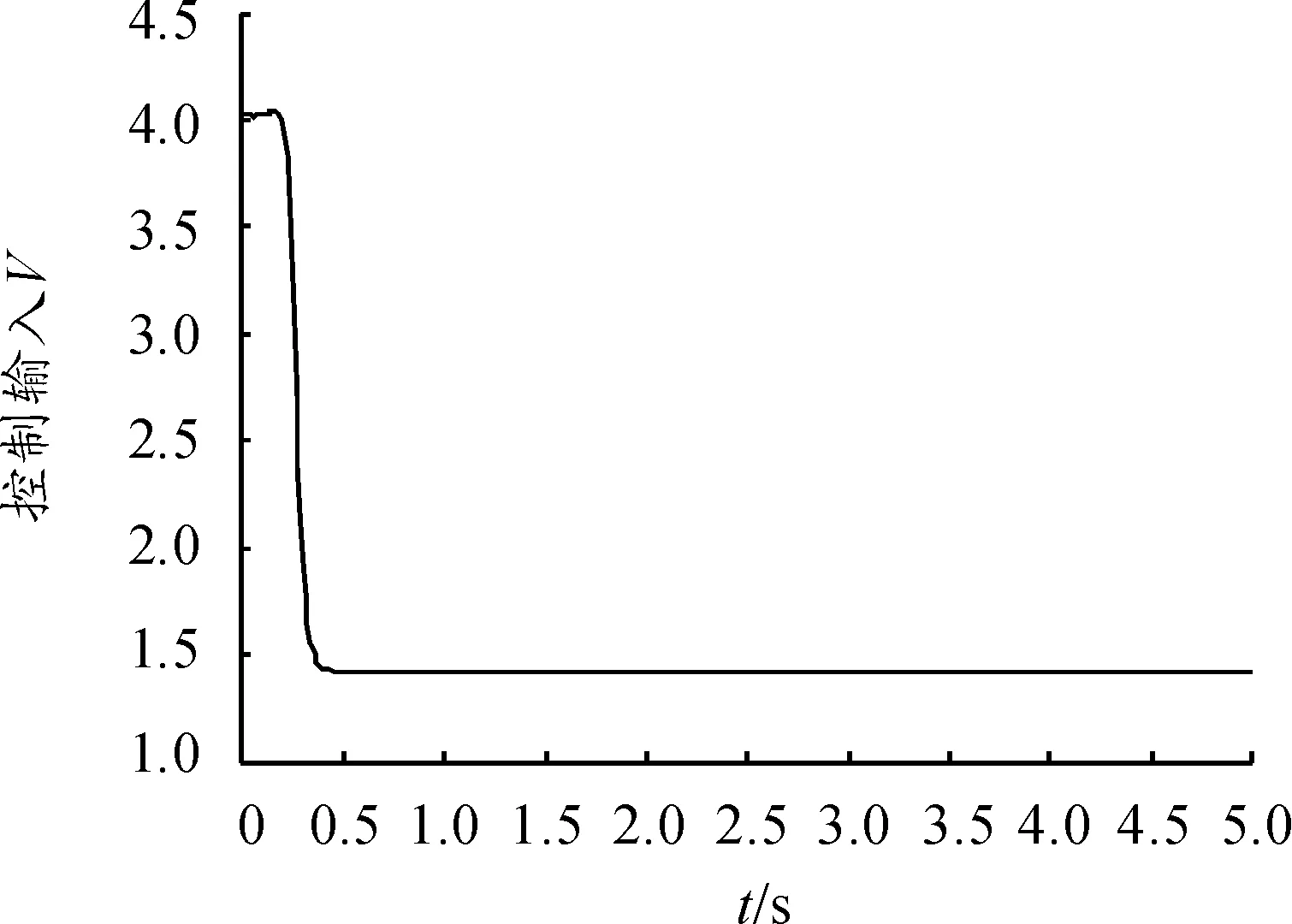
图9 直线跟踪速度V输出曲线

4.3 三段式自动泊车路径跟踪控制

设置车辆自动泊车的起始位置，采用几何方法规划出理想泊车路径，通过对分段曲线进行拟合生成自动泊车路径。选取仿真实验中泊车起始位置，使用本文所设计的路径跟踪控制器对理想泊车路径进行跟踪。仿真中车辆初始位置及姿态取：

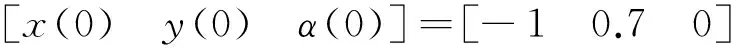
三段式自动泊车路径跟踪控制仿真结果如图10、11所示。图10显示：由于泊车路径跟踪过程中的转角变化较为平缓，从跟踪起点处就开始快速收敛，最终在x<0.5 m内收敛为0，路径跟踪效果好，可以实现一次性成功泊车入位。图11显示：整个自动泊车跟踪过程中车速均未超过5 km/h，满足自动泊车最高车速不高于8 km/h的要求。

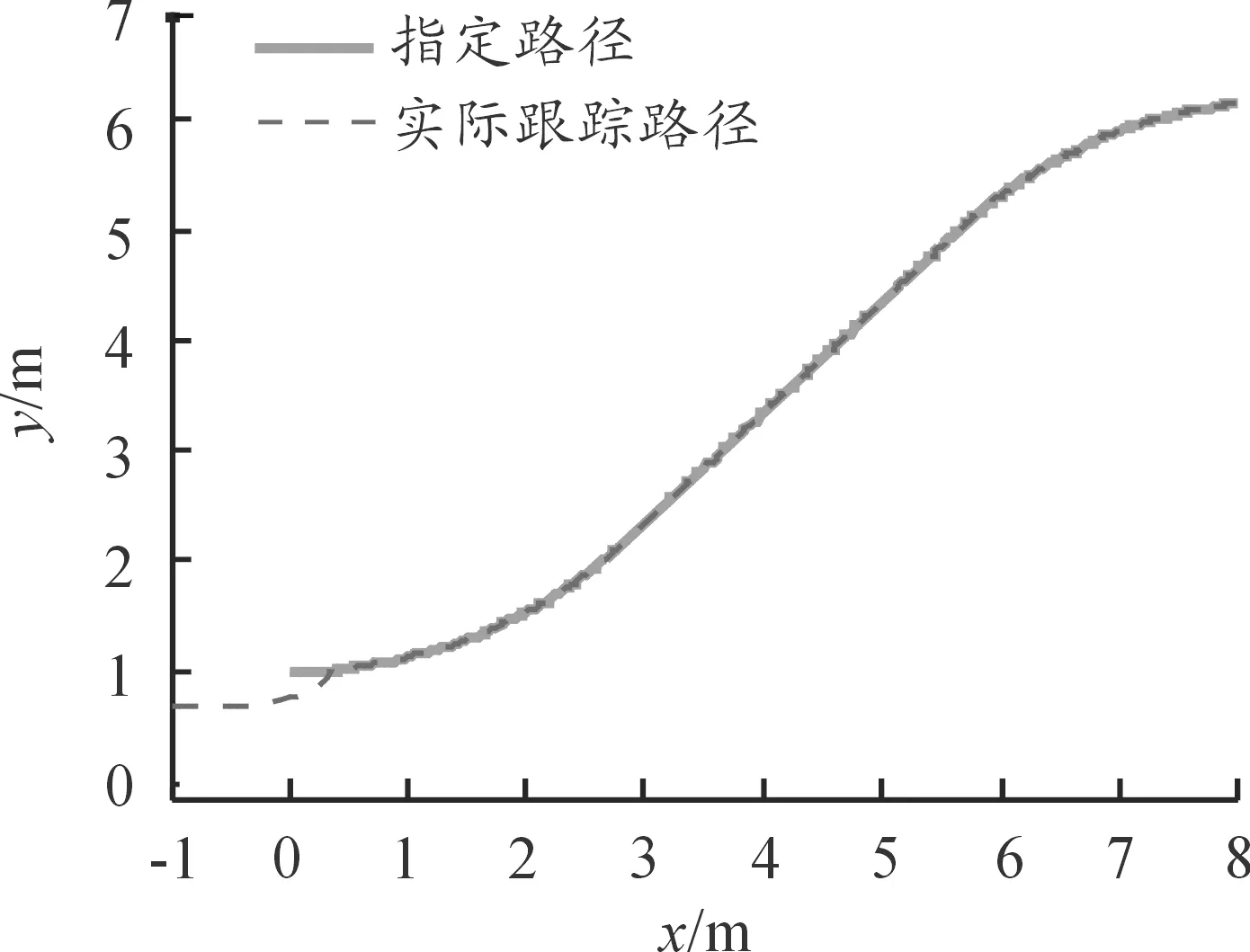
图10 泊车路径跟踪

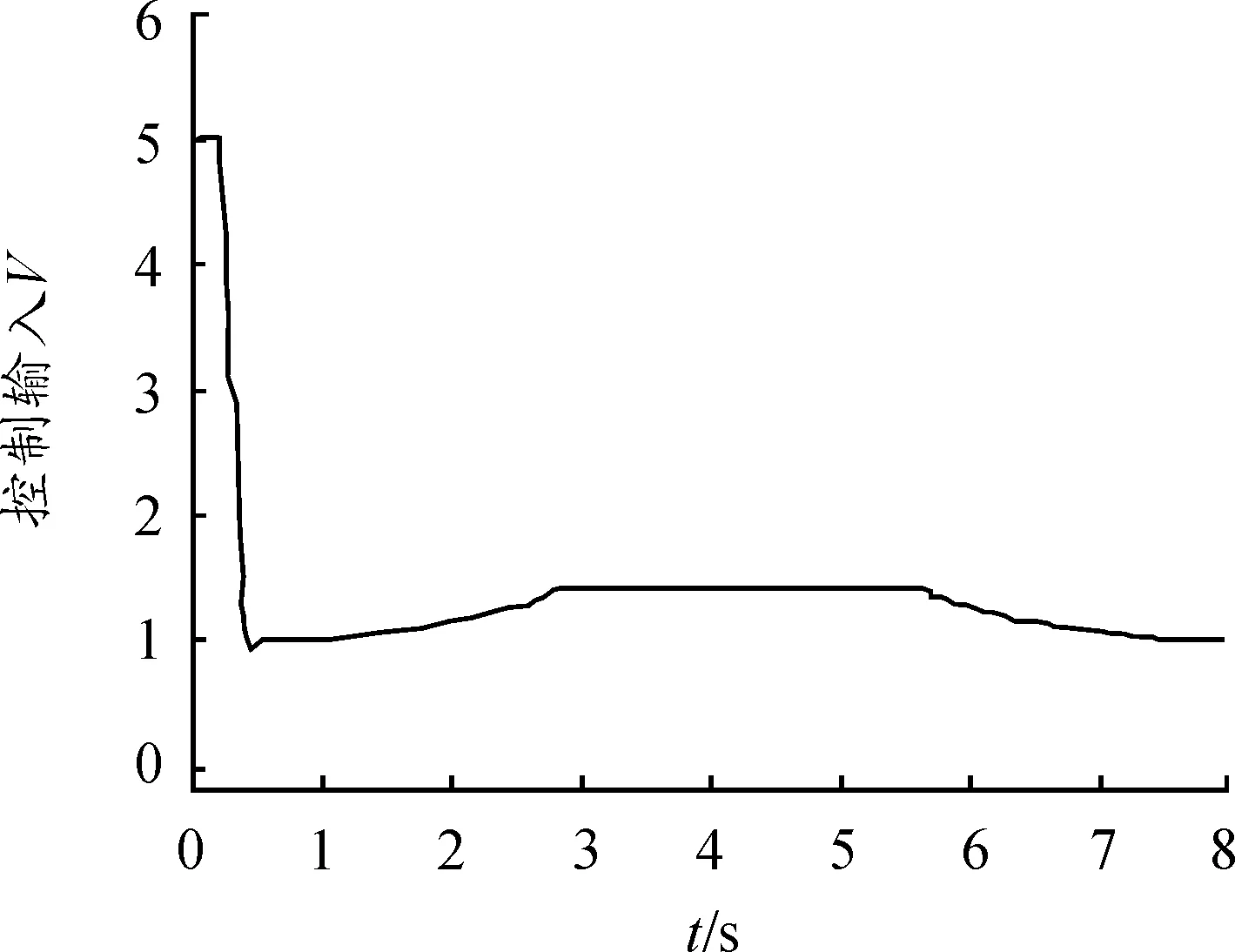
图11 泊车直线跟踪速度V输出曲线

4.4 先进性分析

图12为基于指数趋近控制律得出的三段式泊车路径跟踪仿真结果。通过图10和图12比较可得：采用本文设计的指数和幂次相结合趋近律的控制方法能实现更好的快速收敛，具有更好的平滑性。

综合以上的仿真结果可以看出，无论是圆弧轨迹跟踪、直线轨迹跟踪、三段式路径跟踪，在不同的初始位置和姿态下，采用基于双闭环滑模控制算法的自动泊车控制器都能保证系统误差快速收敛至0，车辆在滑模变结构控制下具有较好的渐进稳定性。

5 结束语

针对自动泊车系统倒车入库时由于路径跟踪导致的最终停车位置不理想的问题，本文设计了基于双闭环滑模结构的自动泊车路径跟踪控制器。通过分析Matlab/Simulink输出的仿真跟踪轨迹，验证了本文所设计的自动泊车路径跟踪控制算法能有效实现泊车倒车路径的精确跟踪，使车辆最终停靠在停车位中。该路径跟踪控制算法计算量小，控制精度较好，时效性较高，可有效提高自动泊车系统的泊车性能，具有较好的实际应用价值和推广价值。

[1] 吴狄.智能泊车与EPS集成控制系统设计与实现[D].镇江：江苏大学,2015.

[2] HSU T H,LIU J F,YU P N,et al.Development of an automatic parking system for vehicle[C]//Vehicle Power and Propulsion Conference,.VPPC’08.China：IEEE， 2008:1-6.

[3] ZHAO Y,DING F,GUO L,et al.Navigation controller design using fuzzy logic theory for vehicle parallel automatic parking [J].Journal of the Balkan Tribological Association,2016,22(2):1289-1298.

[4] VOROBIEVA H,GLASER S,MINOIU-ENACHE N,et al.Automatic parallel parking in tiny spots:Path Planning and Control[J].IEEE Transactions on Intelligent Transportation Systems,2015,16(1):396-410.

[5] 郭孔辉,李红,宋晓琳,等.自动泊车系统路径跟踪控制策略研究[J].中国公路学报,2015,28(9):106-114.

[6] 钱立军,胡伟龙,刘庆,等.多段式自动泊车路径规划及其关键技术[J].吉林大学学报(工学版),2016,46(3):785-791.

[7] 李臣旭.基于车位场景智能识别技术的全自动垂直泊车系统研究[D].镇江：江苏大学,2016.

[8] PAROMTCHIK I E,LAUGIER C.Motion generation and control for parking an autonomous vehicle[C]//1996 IEEE International Conference on Robotics and Automation.USA： IEEE,1996,4:3117-3122.

[9] OUADAH N,LAMINE O,FARES B.Car-like mobile robot oriented positioning by fuzzy controllers[J].International Journal of Advanced Robotic Systems,2008,5(3):249-256.

[10] 任坤,许艺,丁福文,等.基于机器视觉和模糊控制的自动泊车[J].华中科技大学学报(自然科学版),2015,43(393s1):88-92.

[11] 张放,党睿娜,李克强.基于模糊逻辑的自动平行泊车控制方法[J].汽车工程,2014(9):1151-1156.

[12] 赵熙俊，陈慧岩.智能车辆路径跟踪横向控制方法的研究[J].汽车工程,2011(5):382-387.

[13] TONGTONG C,BIN D,JINZE S,et al.On lateral fractionalorder controller in auto-parking system[C]//Control Confe-rence(CCC),2011 30th Chinese.China：IEEE,2011:3429-3434.

[14] LI D.The achievement of automatic parking control system of lifting and transferring stereo garage based on real-time exchange parking stall[C]//International Conference on Electric Information and Control Engineering.China：IEEE,2011:3657-3660.

[15] MALKIN I G.On the reversibility of Lyapunov’s theorem on asymptotic stability[C]//CIME 14 Conference.China:[s.n.],2014:129-138.

(责任编辑杨黎丽)

AutomaticParkingPathFollowingControlBasedonDoubleClosed-LoopSlidingModeStructure

JIANG Haobina, SHEN Zhengnana, MA Shidianb

(a.School of Automobile and Traffic Engineering; b.Automotive Engineer Research Institute, Jiangsu University, Zhenjiang 212013, China)

In order to improve the accuracy of path tracking control in automatic parking system and ensure the success rate of automatic parking into the small target parking spaces, a double closed-loop sliding mode variable structure tracking control method was proposed. The tracking system of the vehicle kinematic model was transformed into a double closed-loop cascade subsystem with position controller and attitude controller, and a convergence law of exponential and power was designed to ensure the parking path achieves rapid convergence in a limited time, so that the parking tracing path could achieve rapid convergence in a limited time. Based on Matlab/Simulink, the tracking control model was built. The simulation results showed that the path tracking control algorithm designed in this paper could ensure that the tracking point converges to the ideal path, which improves the success rate of automatic parking storage.

automatic parking; path tracking; sliding mode control

2017-02-20

江苏省产学研前瞻性联合创新项目(BY2012173)

江浩斌(1969—),男,江苏人,博士,教授，主要从事车辆动力学性能分析与电控技术、道路车辆运行安全主动防控技术及理论和智能交通运输技术等研究，E-mail：jianghb@ujs.edu.cn。

江浩斌，沈峥楠，马世典.基于双闭环滑模结构的自动泊车路径跟踪控制[J].重庆理工大学学报(自然科学)，2017(10):6-11,27.

formatJIANG Haobin, SHEN Zhengnan, MA Shidian.Automatic Parking Path Following Control Based on Double Closed-Loop Sliding Mode Structure[J].Journal of Chongqing University of Technology(Natural Science)，2017(10):6-11,27.

10.3969/j.issn.1674-8425(z).2017.10.002

U461.6

A

1674-8425(2017)10-0006-06