球体垂直入水过程流体动力数值研究

孙 钊， 曹 伟， 王 聪

(哈尔滨工业大学 航天学院，哈尔滨 150001)

球体垂直入水过程流体动力数值研究

孙 钊， 曹 伟， 王 聪

(哈尔滨工业大学 航天学院，哈尔滨 150001)

采用VOF(Volume of Fluid)多相流模型耦合CSF(The Continuum Surface Force Model)模型，对亲水性及疏水性球体垂直入水过程进行了数值研究。将数值结果与文献实验结果对比，验证了数值方法的可靠性。在此基础上，开展亲水性及疏水性球体垂直入水数值研究。结果表明，亲水性球体在较低入水速度下不产生入水空泡，而疏水性球体产生较大入水空泡，空泡在自由液面以下某一位置闭合形成“沙漏状”空泡形态。入水初期在球体表面形成液体薄层运动是导致空泡形成与否的关键因素,对于亲水性球体，液体薄层沿球体表面向上运动并在球体顶点位置汇聚形成向上的溅射流，不产生入水空泡；对于疏水球体，液体薄层在球体赤道位置附近与球体表面分离，导致空气进入，形成入水空泡。通过球体入水过程运动轨迹、速度、加速度，分析了表面润湿性及密度对球体入水过程运动参数的影响。最后，分析了球体入水过程中受到的总流体动力，发现亲水性球体在垂直入水过程中下落速度更快，守到更小的总流体动力，表明其受到更小的阻力。

球体；入水空泡；润湿性；数值研究；流体动力

入水问题是一个较复杂的固体及液体相互作用问题。在物体入水过程中伴随着许多现象，例如撞击瞬间，喷溅产生，入水空泡，面闭合，空泡深闭合，空泡溃灭等．许多工程问题及自然现象都涉及入水问题，例如船舶砰击[1]，跳弹[2]，空投鱼雷[3]，水上行走生物[4]等．

大量有关物体入水的研究，寻求定性和定量的表征入水过程中发生的流体动力现象以及在撞击液面过程中物体受到的力。Von Karman[5]最早研究这种现象，他分析了水上飞机在着陆过程中的受力。随后有关入水问题的研究主要集中在军事实验室实施的弹道学研究。May[6]开展了有关自由液面撞击问题的大范围实验研究。他的研究主要集中于探索在高速情况下跟随圆形物体尾部的入水空泡产生。

高速成像技术在捕捉入水过程撞击现象发生的瞬间过程至关重要，并且在早期入水问题已经得到广泛应用。研究者们应用数字高速成像技术开展了大量有关球体及其他物体的入水实验研究，例如Bell等[7-12]。

前人大多数的研究工作都集中于运动体的几何形状、入水姿态、入水速度等对入水现象的影响，近年来运动体的表面状态，尤其是表面润湿性对入水问题的影响逐渐得到关注，然而相关研究依旧较少。Worthington[13]对球体的垂直入水现象进行了大量的实验研究，发现球体沾湿后入水不易产生空泡，而在球体表面涂一层烟灰后将产生较大的入水空泡。Duez等[14]研究了不同表面润湿性球体的入水现象，发现只有在入水速度超过某一临界值的情况下才会产生入水空泡，并且表面润湿性对该临界值的大小有较大影响。Doquang等[15]通过耦合Navier-Stokes方程以及Cahn-Hilliard方程方法，利用数值计算模拟了不同表面润湿性球体在不同液体介质中的运动,计算结果获得了大量的入水空泡矢量场图片。Abraham等[16]采用VOF方法及SST(the Shear Stress Transport)湍流模型模拟了球体入水初期的阻力系数，研究中所选用的球体密度与水的密度极其接近，ρ*=ρsphere/ρfluid≈1.1，并且没有考虑表面润湿性。

本文通过数值方法研究球体的垂直入水过程，重点考虑表面润湿性这一影响因素，同时为了便于探索球体入水过程中的流体动力，针对不同密度的球体展开研究。本文首先介绍了数值方法，然后通过与文献中实验结果对比说明了数值方法的准确性。随后，在此基础上，通过对入水初期空泡发展过程的观察探索入水空泡的生成机理和发展过程，分析了入水过程中表面润湿性及密度对球体运动轨迹、速度、加速度的影响。最后，探讨了球体入水过程受到的流体动力。

1 数值方法

1.1 控制方程

本文研究对象为球体低速入水问题，球体只做竖直方向运动，因此该问题简化为三维不可压缩二相流问题。流动控制方程为式(1)及式(2)，分别代表动量守恒及质量守恒。

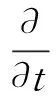
(1)

·u=0

(2)

式中：ρ为混合物密度；u为速度矢量；μ为混合物动力黏度；p为压强；g为重力加速度。F为加入到动量方程中的表面张力效应源项。

1.2VOF模型

数值计算采用VOF多相流模型描述计算流域中气相及液相体积分数，该方法为每一相引入了一个体积分数变量: 令液相的体积分数为αl,则

αl=0：代表该网格单元没有液相分布；

αl=1：代表该网格单元全部为液相；

0<αl<1：代表该网格单元同时包含液相及气相，并且相界面由此定义；

本文定义αl=0.5代表气相与液相的交界面。对于二相流问题，气相的体积分数即为1-αl。混合物密度以及混合物粘度分别为式(3)及式(4)。

ρ=ρlαl+ρg(1-αl)

(3)

μ=μlαl+μg(1-αl)

(4)

式中：αl为液相体积分数；ρl,ρg,μl,μg分别为液相及气相的密度和动力黏度。具体数值见表1。

表1 数值过程中液相及气相属性Tab.1 Properties of liquid and gas phase in numerical process

1.3 CSF模型

本文采用Brackbill等[17]提出的CSF模型描述表面润湿性，将表面张力项作为源项加入到动量方程中:

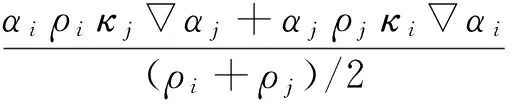
(5)

对于二相流问题，κi=-κj,αi=-αj, 因此，表面张力项简化为

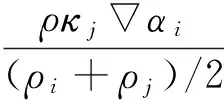
(6)

式中：ρ为式(3)中的混合物密度。κ=αq。

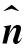
(7)

1.4 湍流模型

本文数值计算采用标准k-ε湍流模型[18].μt通过湍动能k及湍动能耗散率ε求解

(8)

式中：Cμ为常数，湍动能k,及其耗散率ε分别为

Gb-ρε

(9)

(10)

式中：Gk为由平均速度梯度所引起的湍动能生成项,Gb为由浮力所引起的湍动能生成项。经验常数C1ε,C2ε,Cμ,σk,σε分别为:C1ε=1.44,C2ε=1.92,Cμ=0.09,σk=1.0,σε=1.3，C3ε=tan|uw/un|,uw为平行于重力矢量的流速分量，un为垂直于重力矢量的流速分量。

1.5 计算域及边界条件

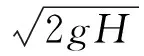
如图1所示，边界条件分别为压力入口、压力出口、固体壁面边界、对称平面。压力入口及压力出口处分别设置压强、气相及液相体积分数、湍动能及其耗散率，固体壁面边界设置为无滑移壁面，对称平面通过球体中心。竖直向下为z轴正向，自由液面所处的水平面为z轴零点z=0，球体在运动过程中只在z方向有位移，在x，y方向均不作任何位移。

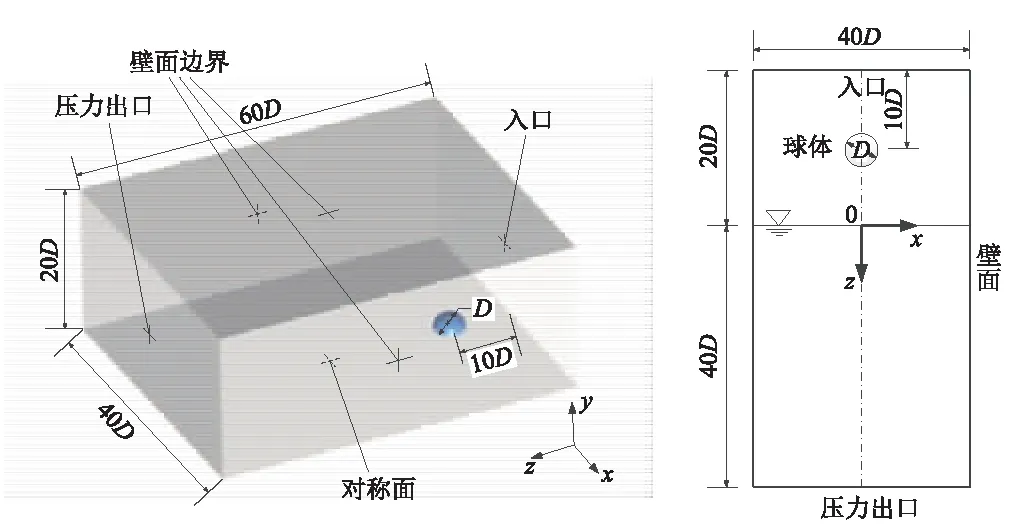
图1 计算域及边界条件Fig.1 Computational domain and boundary condition

1.6 计算设置

本文应用的数值计算软件为ANSYS FLUENT，边界条件设置、计算流域初始化、自编程序的编译等均在软件界面中设置。数值计算过程中，采用有限体积法对流动控制方程离散；压力场与速度场的耦合选用PISO算法；压力场的空间离散采用PRESTO！格式；各相体积率离散采用CICSAM格式；各求解变量的离散采用二阶迎风格式；对流项采用QUICK离散格式；相界面的几何重构采用Geo-Reconstruct格式。数值计算过程中，引入UDF自编程序实现运动体的竖直方向运动。

2 结果与分析

2.1 数值结果验证

本文通过与Truscott等[20]中的实验结果对比，以验证数值方法的准确。数值计算获得的空泡形态与实验图片分别示于图2及图3中。

如图2所示，球体入水速度U0=1.72 m/s，球体表面为亲水性表面，表面接触角θ=60°，数值计算过程中的入水条件设置与实验一致。在这种亲水性球体的入水现象中，球体撞击自由液面后仅有一个垂直向上的溅射流产生.随球体下落，在自由液面以下没有形成入水空泡，球体完全被液体包裹，数值结果与实验结果有很高的吻合度。

图2 亲水性球体数值结果与实验结果对比Fig.2 Comparison of the numerical result with the experiment result of the water entry cavities created by hydrophobic sphere

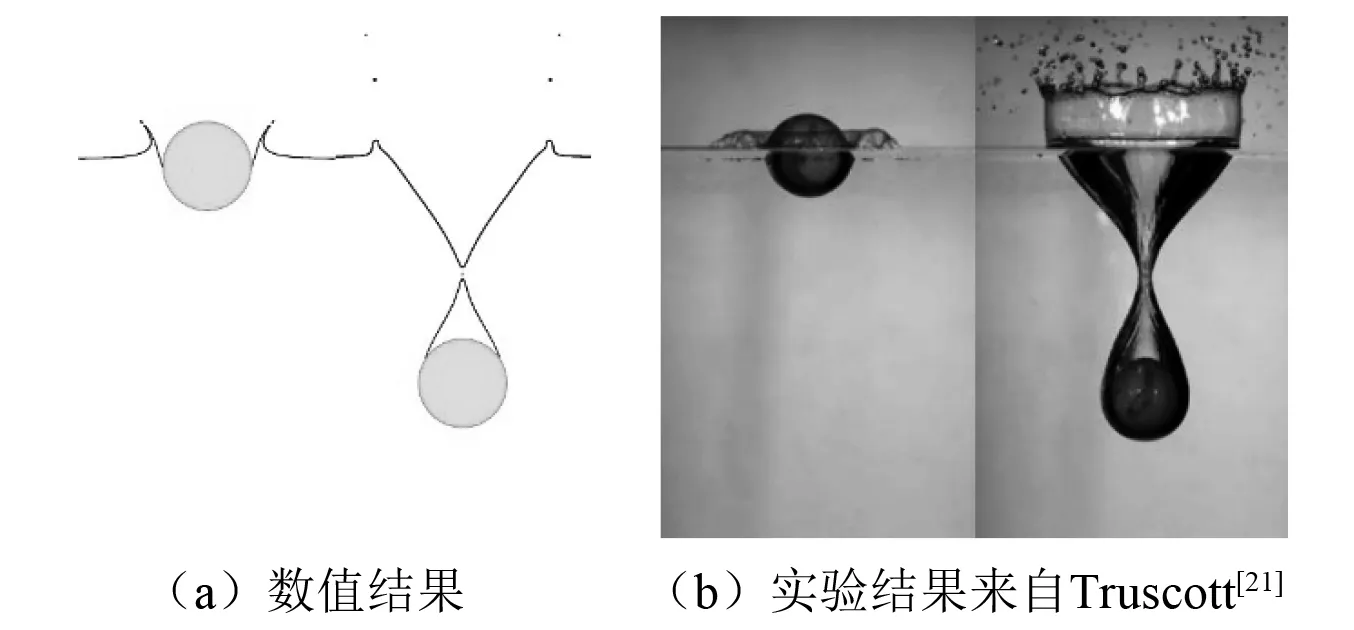
图3 疏水性球体数值结果与实验结果对比Fig.3 Comparison of the numerical result with the experiment result of the water entry cavities created by hydrophobic sphere

图3为另一组数值结果与实验图片对比。其中，球体表面为疏水性表面，表面接触角θ=120°，入水速度U0=1.72 m/s，同样与实验条件保持一致。在这种疏水性球体的入水现象中，入水初期液体在球体表面某一位置分离并形成入水空泡，随后空泡在自由液面以下某一深度掐断(深闭合)形成经典的“沙漏状”空泡形态，数值结果与实验图片对应良好。

2.2 空泡形态

图4为密度不同的亲水性球体入水过程，三球体具有相同的入水速度U0=2.37 m/s(相当于从高度300 mm 自由下落)以及完全一致的亲水性表面θ=30°，球体密度分别为ρ*=1.2，2.7，7.8，每组图片之间的时间间隔均为Δt=8 ms。从图4中可以看出，密度越大的球体下落速度更快，然而它们的入水现象没有太大差别，均没有空泡产生，仅仅在自由液面以上形成垂直向上的溅射流。

图5为三个不同密度疏水性球体的入水空泡发展过程，三球体具有相同的入水速度U0=2.37 m/s(相当于从高度300 mm 自由下落)以及完全一致的表面润湿性θ=150°，球体密度不同，分别为ρ*=1.2，2.7，7.8，每组图片之间的时间间隔均为Δt=8 ms。从图5中可以看出，密度越大的球体下落速度更快并且空泡闭合位置更深，球体入水过程的空泡闭合时间基本保持一致，说明入水球体密度对闭合时间没有明显影响。

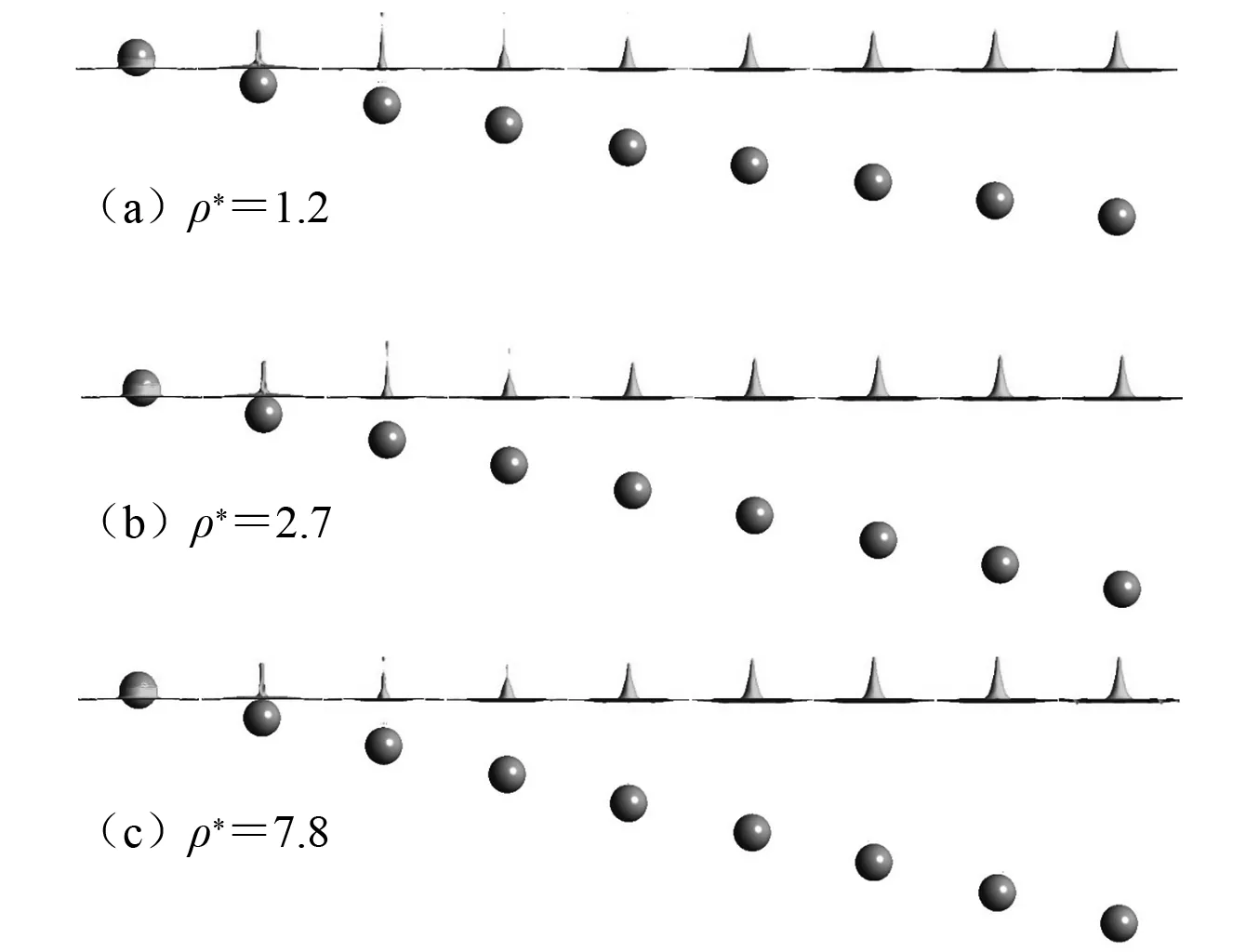
图4 不同密度亲水性球体入水空泡发展过程Fig.4 The water entry cavities created by hydrophilic spheres with different density

图5 不同密度疏水性球体入水空泡发展过程Fig.5 The water entry cavities created by hydrophobic spheres with different density

图4及图5示出了不同密度亲水性 (0°<θ<90°) 球体及疏水性 (90°<θ<180°) 球体入水现象的基本差异。对比图4及图5，球体直径完全一致，并且具备同样的入水运动参数，然而仅仅表面润湿性的不同就会对入水现象产生显著影响：对于疏水性球体的入水过程，形成了入水空泡，空泡逐渐发展并且在自由液面以下某一深度闭合；对于亲水性球体的入水，仅仅有垂直向上的溅射流产生，没有形成入水空泡。

Korobkin等[22]探索了运动体撞击自由液面的入水初期阶段.研究指出，入水初期在运动体表面形成液体薄层并沿运动体表面向上运动。该现象从图6中可以清晰的看到。如图6所示，入水初期在球体表面形成液体薄层，并且亲水性球体和疏水性球体在入水初期就已经开始呈现差异较大的入水现象。对于亲水性球体，如图6(a)，产生的液体薄层沿球体表面向上运动，并最终在球体的顶部汇合，这种情况不会产生入水空泡；对于疏水性球体，如图6(b)所示，液体薄层在运动到球体赤道附近处发生分离，从而导致空气的进入并形成入水空泡。

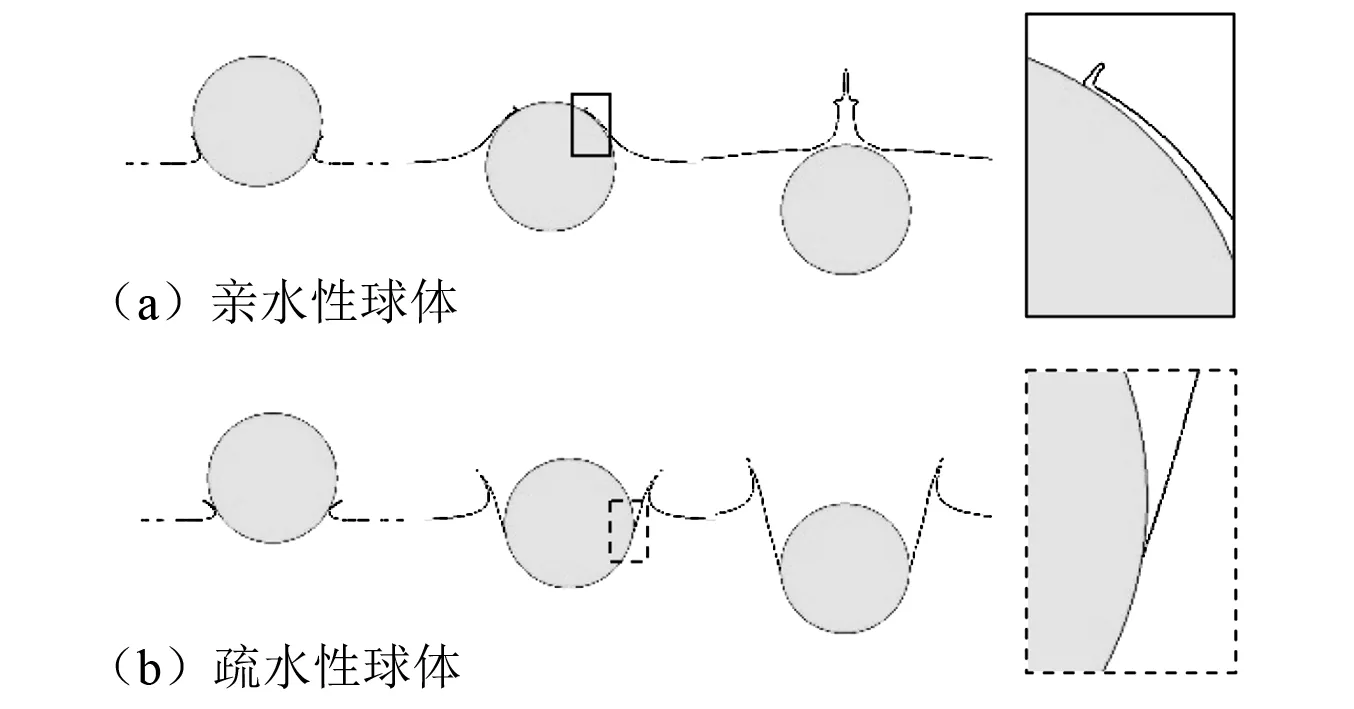
图6 不同润湿性球体入水初期产生的液体薄层Fig.6 The fluid film created during the initial stage of impact

2.3 轨迹、速度、加速度

表面润湿性以及密度不仅影响球体的入水空泡形态，对球体入水过程的运动轨迹、速度、加速度同样具有一定影响。

图7为不同密度的两种表面润湿性球体的运动位移随时间的变化，并对各个量进行了无量纲化。时间零点选于球体接触水面瞬间的时刻，D=25.4 mm为球体直径，tds=65 ms为图5中疏水性球体产生入水空泡的闭合时间。取竖直向下为正(图1中z轴正向)，因此球体的位移、入水速度矢量以及重力加速度矢量均为正。球体密度分别为ρ*=1.2，2.7，7.8，球体表面接触角分别为θ=30°，150°。

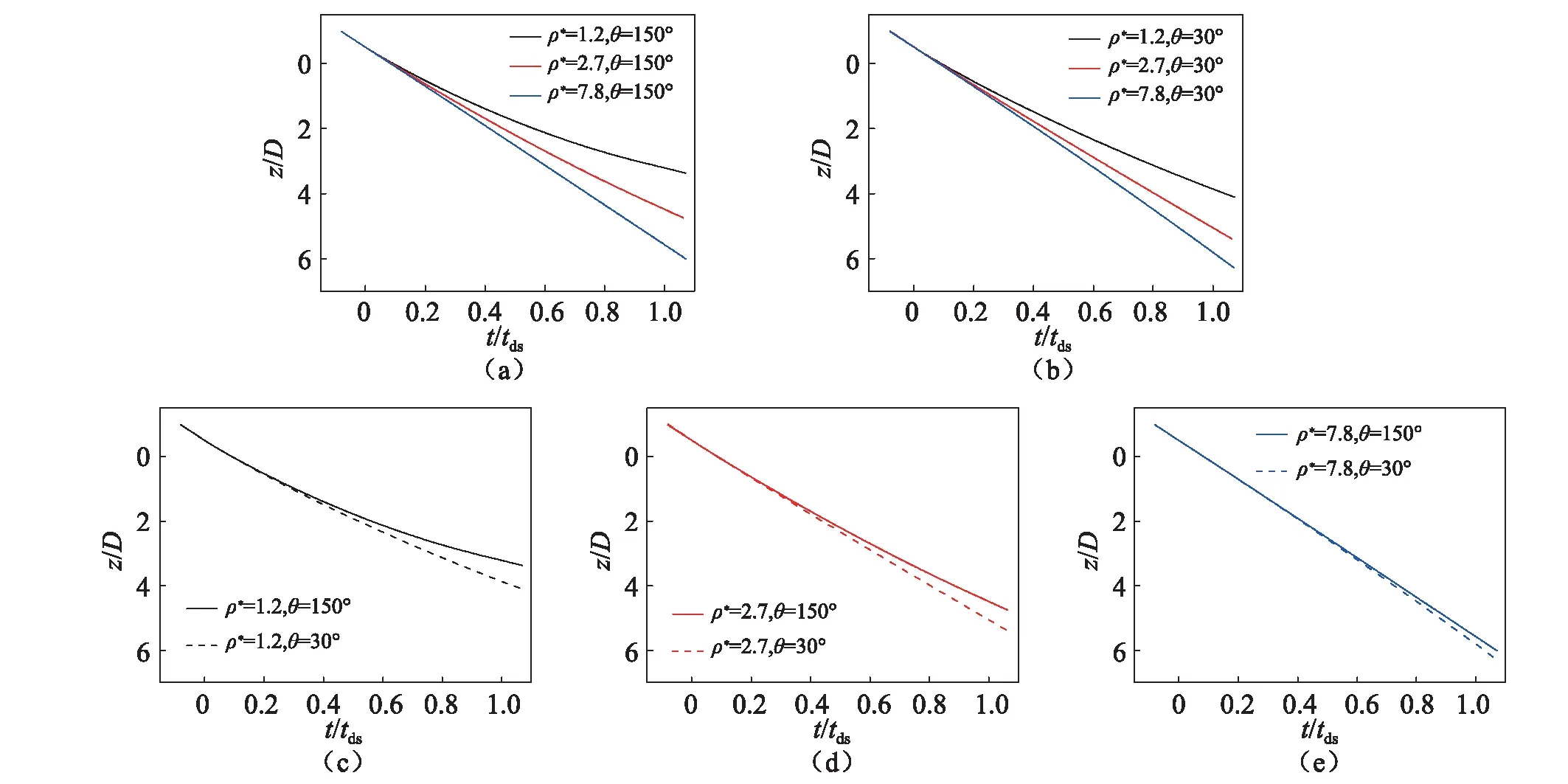
图7 球体入水过程运动位移随时间的变化Fig.7 Position versus time for different sphere during water entry

图7(a)、(b)分别为表面接触角θ=150°，30°不同密度球体的位移变化，可以明显看出密度越小，球体下降速度越缓慢。图7(c)、(d)、(e)为相同密度球体在不同表面润湿性条件下的位移随时间变化，可以看出亲水性球体(图中θ=30°)下降速度普遍更快，说明流体对亲水性球体的阻力相对更小。

图8为球体入水过程速度-时间曲线，入水速度

U0=2.37 m/s。如图8所示，时间零点之前(t/tds≤0)为自由落体运动，因此速度逐渐增大；在入水初期极短时间内(0≤t/tds≤0.1)，速度均有一个明显的减小过程，并且低密度(ρ*=1.2)的球体速度衰减更快；随后(t/tds≥0.1)，不同球体的速度以不同变化率逐渐改变，其中密度较大ρ*=7.8的球体速度逐渐增大，处于加速状态，密度较小ρ*=1.2的球体做明显的减速运动。

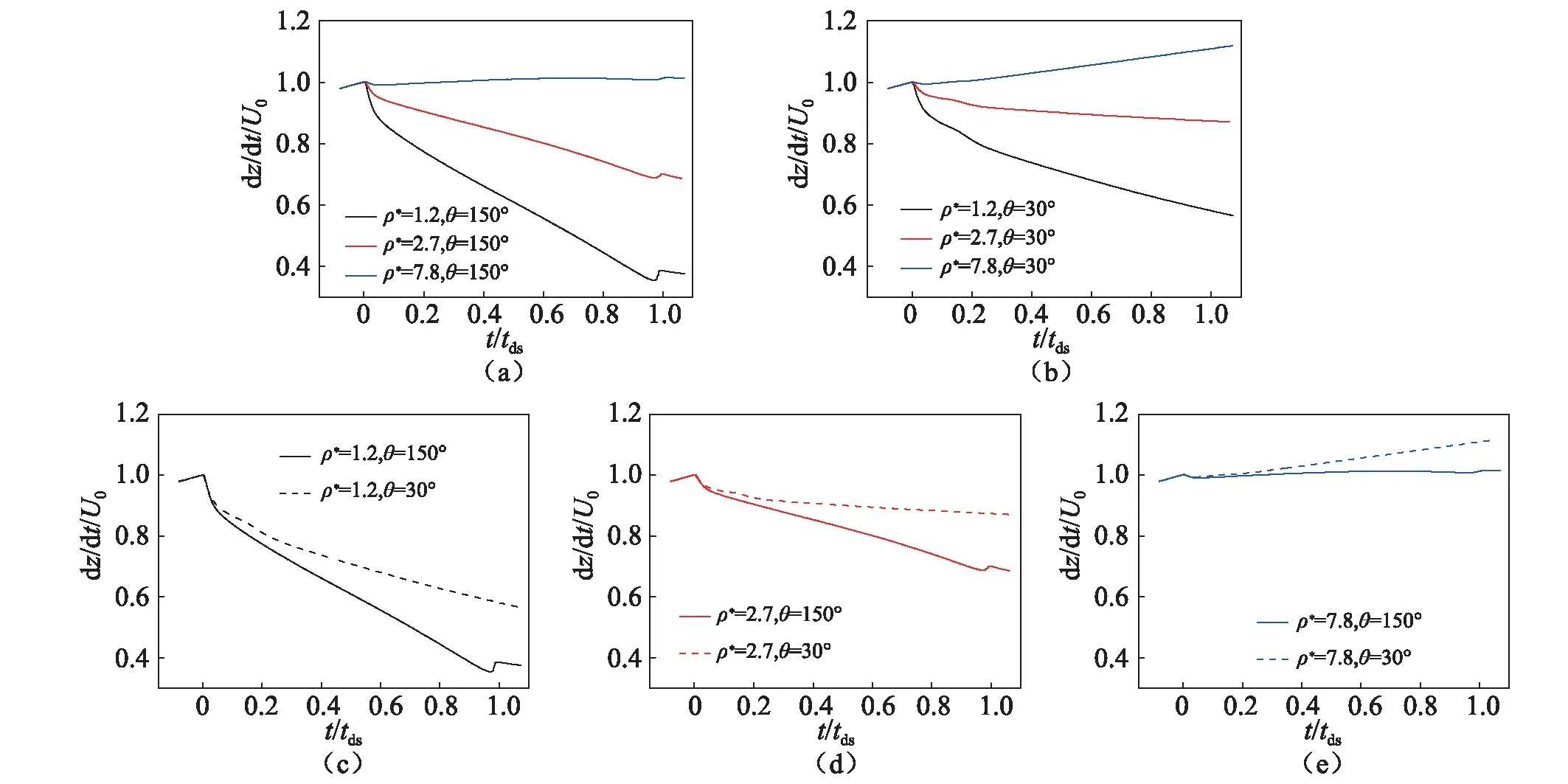
图8 球体入水过程速度变化Fig.8 Velocity versus time for different sphere during water entry

图8中，在t/tds=1时刻左右(图5中入水空泡闭合时刻)，速度曲线出现了一个扰动，这是由于入水空泡深闭合使空泡内部压强出现扰动所致。对于密度较低的球体，这种扰动尤为明显。对于亲水性球体的入水过程，由于不产生入水空泡，因此没有这样的扰动出现。图8(c)、(d)、(e)为密度相同而表面润湿性不同的球体入水过程速度随时间变化，从图中看出，亲水性球体其速度衰减的更慢，致使密度相同的亲水性球体速度大于疏水性球体速度。

图9给出球体入水过程加速度随时间的变化。从图9中可看出，球体在撞水瞬间有一个较强的向上的加速度(负值代表与重力加速度方向相反)，这是由于入水撞击瞬间产生的冲击造成。随后疏水性球体的加速度回升至一个较平缓的阶段直至空泡闭合，且密度较低的球体其加速度量值在任何时刻都比高密度的球体大，因此速度变化的更显著。

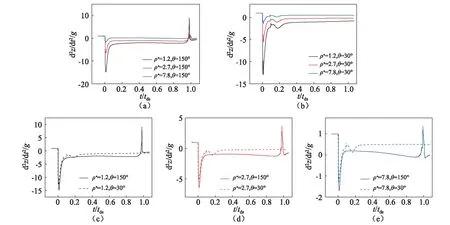
图9 球体入水过程加速度变化Fig.9 Acceleration versus time for different sphere during water entry

在图9(a)中，空泡闭合瞬间(t/tds=1)，加速度呈现了大小约为(d2z/dt2/g=3～8且方向与重力加速度相同，说明球体在极短时间内处于加速下落状态，球体运动速度也在这一时刻发生了波动。在图9(b)中，亲水性球体在经历入水冲击(0≤t/tds≤0.1)，加速度又经历了一个较小波动(0.1≤t/tds≤0.2)后才趋于平缓。这应该由于亲水性球体在入水初期产生的液体薄层沿球体表面向上运动，并在球体顶部汇合导致。图9(c)、(d)、(e)为密度相同然而表面润湿性不同的球体入水过程加速度随时间变化。从图中看出，亲水性(θ=30°)球体其加速度的量值相对较小，说明亲水性球体受到更小的阻力。

2.4 流体动力分析

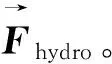
(11)

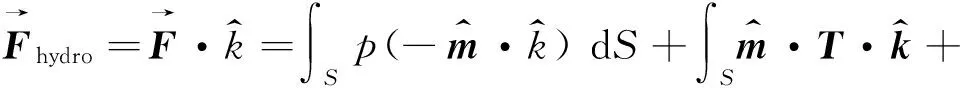
(12)

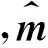
(13)

式中：U(t)为不同时刻的瞬时速度，ρ=ρfluid为液体密度，本文中ρfluid=998.2 kg/m3。

图10给出球体入水过程的总流体动力系数随时间的变化。从图10中可以更清晰的看出在入水过程中不同表面润湿性及密度对总流体动力的影响。图10(a)中，在入水初期t/tds≤0.4时间段，不同密度球体的总流体动力系数相似，没有太大差别；t/tds≥0.4后，低密度球体的总流体动力系数量值逐渐增加且为负值；在闭合时刻t/tds=1，总流体动力系数呈现一个较大的正峰值，说明此时刻流体作用力有一个瞬间推动球体加速下落的过程。图10(b)为亲水性不同密度球体的总流体动力系数。初期阶段t/tds≤0.4，三种球体的流体动力系数变化规律及大小大体相似。图10(c)、(d)、(e)为密度相同、表面润湿性不同的球体入水过程总流体动力系数随时间变化，从图中看出，亲水性(θ=30°)球体其总流体动力系数的量值相对较小，说明在入水过程中亲水性球体的总流体动力较小。

图10 球体入水过程流体动力系数Fig.10 The coefficient of hydrodynamic force for different spheres during water entry

3 结 论

本文通过数值方法研究了不同密度、不同表面润湿性球体的垂直入水过程，对入水空泡形态以及入水过程中球体轨迹、速度、加速度、流体动力进行了分析。对于更宽广入水条件的研究，例如更高的入水速度以及更复杂的几何运动体，有待于进一步探索。本文主要得到以下结论：

(1)本文所采用的VOF耦合CSF数值方法可以准确的模拟不同润湿性表面球体的入水现象，并且与实验结果有较高的吻合度。

(2) 入水初期在球体表面形成液体薄层。对于亲水性球体，液体薄层沿球体表面向上运动，并最终至球体顶点汇聚，不产生入水空泡。对于疏水性球体，液体薄层在球体赤道附近与球体表面分离，形成入水空泡。

(3)对于疏水性球体，入水空泡在闭合瞬间将对球体产生一个较强冲击作用，体现为推动球体加速下落；亲水性球体由于不产生入水空泡，不会有这样的现象出现。

(4)对于亲水性球体，在入水初期(0.1≤t/tds≤0.2)流体作用力因为液体薄层的运动，出现较小的扰动；疏水性球体由于液体薄层的及早分离，没有这样的扰动。

(5) 相对于疏水性球体，亲水性球体下落速度更快，受到的来自于流体的总流体动力更小，说明阻力更小。

[1] FALTINSEN O M, ZHAO R. Water entry of ship sections and axisymmetric bodies[J]. AGARD Q2 FDP and Ukraine Institute of Hydromechanics Workshop on High-Speed Body Motion in Water,1997, 24: 11.

[2] ROSELLINI L, HERSEN F, CLANET C, et al. Skipping stones[J]. J Fluid Mech, 2005, 543: 137-146.

[3] MAY A. Vertical entry of missiles into water[J]. J Appl Phys, 1952, 23: 1362-1372.

[4] BUSH J W M, HU D L. Walking on water: Biolocomotion at the interface[J]. Annu Rev Fluid Mech, 2006, 38: 339.

[5] VON KARMAN T. The impact on seaplane floats during landing[C]∥ Technical Notes 321. National Advisory Committee for Aeronautics, Aerodynamic Institute of the Technical High School. Aachen, 1929.

[6] MAY A. Water entry and the cavity-running behaviour of missiles[R]. Silver Springs, MD: Final Naval Surface Weapons Center White Oak Laboratory, 1975.

[7] BELL G E. On the impact of a solid sphere with a fluid surface[J]. Phil Mag, 1924, 48: 753-764.

[8] MAY A, WOODHULL J C. The virtual mass of a sphere entering water vertically[J]. J App Phys, 1950, 21:1285-1289.

[9] RICHARDSON E G. The impact of a solid on a liquid surface[J]. Proc Phys Soc, 1948, 4: 352-367.

[10] MAY A. Effect of surface condition of a sphere on its water-entry cavity[J]. J Appl Phys, 1951, 22: 1219-1222.

[11] MAY A, HOOVER W R. A study of the water-entry cavity[J]. Unclassified NOLTR, 1963,63: 264.

[12] ABELSON H I. Pressure measurements in the water-entry cavity[J]. J Fluid Mech, 1970, 44: 129-144.

[13] WORTHINGTON A M. A study of splashes[M]. London: Longmans Green,1908.

[14] DUEZ C, YBERT C, CLANET C, et al. Making a splash with water repellency[J]. Nature Physics, 2007(3): 180-183.

[15] DOQUANG M, AMBERG G. The splash of a solid sphere impacting on a liquid surface: Numerical simulation of the influence of wetting[J]. Physics of Fluids, 2009, 21: 022102.

[16] ABRAHAM J, GORMAN J, RESEGHETTI F. Modeling and numerical simulation of the forces acting on a sphere during early-water entry[J]. Ocean Engineering, 2014, 76: 1-9.

[17] BRACKBILL J U, KOTHE D B, ZEMACH C. A continuum method for modeling surface tension[J]. J Comput Phys 1992, 100: 335-354.

[18] LAUNDER B E, SPALDING D B. Lectures in mathematical models of turbulence[M]. London :Academic Press, 1972.

[19] GLASHEEN J W, MCMAHON T A. Vertical water entry of disks at low froude numbers[J]. Physics of Fluids, 1996, 8(8): 2078-2083.

[20] TRUSCOTT T T, TECHET A H, Water entry of spinning spheres[J]. Journal of Fluid Mechanics, 2009, 623:135-165.

[21] GILBARG D, ANDERSON R A. Influence of atmospheric pressure on the phenomena accompanying the entry of spheres into water[J]. J Appl Phys, 1948, 19: 127-139.

[22] KOROBKIN A A, PUKHNACHOV V V. Initial stage of water impact[J]. Annu Rev Fluid Mech, 1988, 20: 159.

Numericalinvestigationsofhydrodynamicforceactingonsphereduringwaterentry

SUNZhao,CAOWei,WANGCong

(SchoolofAstronautics,HarbinInstituteofTechnology,Harbin150001,China)

The water entry of hydrophilic and hydrophobic spheres with different density was investigated by numerical simulations. During the simulation, the Reynolds-Averaged-Navier-Stokes equations were solved with the VOF (volume of fluid) method coupled with the CSF method (The Continuum Surface Force Model). Numerical results with different wetting properties and different densities were presented, and directly compared with the experimental results from published literature, showing a good agreement with the experimental results, demonstrating that the simulation methodology is trustable in handling such a problem. Based on this methodology, the water entry cavity created by sphere was investigated. The fluid film developing during the early stage of water entry was shown, which is helpful for illustrating the mechanism of water entry cavity formation. The effect of wetting properties on the sphere’s trajectory, velocity, acceleration was discussed. Finally, the total hydrodynamic forces acting on the sphere during water entry were investigated, showing that the hydrodynamic force acting on hydrophilic sphere was much smaller than hydrophobic sphere, and the hydrophilic sphere descend more quickly during water entry, indicating a much smaller drag force.

sphere water-entry; cavity formation; wet tability; numerical simulation; hydrodynamic force

黑龙江省自然科学基金(A201409)；中央高校基本科研业务费专项资金(HIT.NSRIF.2013033)；哈尔滨市科技创新人才研究专项基金(2013RFLXJ007)

2016-05-24 修改稿收到日期： 2016-07-19

孙钊 男，博士，1985年生

曹伟 男，副教授，1978年生

E-mail:caowei@hit.edu.cn

TB126

A

10.13465/j.cnki.jvs.2017.20.026