两端固定载流管非线性振动IHB方法研究

王 鹏， 张咏鸥， 王 晟， 张 涛

(华中科技大学 船舶与海洋工程学院，武汉 430074)

两端固定载流管非线性振动IHB方法研究

王 鹏， 张咏鸥， 王 晟， 张 涛

(华中科技大学 船舶与海洋工程学院，武汉 430074)

增量平衡谐波法(IHB法)可用于求解两端简支载流管的非线性振动问题。考虑非线性约束及集中质量点的影响，利用Hamilton原理建立两端简支载流管运动微分方程，经Galerkin离散后，通过改变控制变量频率比得到系统的幅频特性曲线。讨论了系统运动参数例如速度、质量比、非线性约束刚度及质量点对系统幅频特性的影响。计算结果表明增量平衡谐波法是一种求解载流管非线性振动较为有效的方法。

载流管；增量平衡谐波法；非线性约束；质量点

载流管(Pipes Conveying Fluid)作为一种常见的载流装置在现代工业中有着广泛的应用：小到生活中常见的自来水管，大到航空航天、海洋工程及能源化工等专用的传送管道[1-2]。同时载流管系统是一个典型的线性-非线性振动系统，在管内低流速时，非线性项对系统的振动影响不大，此时系统的振动可以看作是线性振动，而当系统中某些变量例如流速或压力达到了一定数值时，非线性项不可忽略，此时系统因存在非线性项而为非线性系统。

Lee等[3]首先考虑了管路振动对流体运动状态的影响，推导了非线性耦合的4方程模型，张立翔等[4]则在Lee研究基础上增加了管道轴向运动和横向运动的耦合，得到了较为全面的非线性全耦合模型。Wadham等[5]推导了悬臂管路的三维运动模型，并发现了其非线性方面与二维模型的区别。

针对上述振动微分方程，各种用于求解非线性微分方程的现代计算方法一一提出。最为基础和有效的是基于Galerkin离散的龙格库塔(Runge-Kutta)法[6]。龙格库塔法则是求解常微分方程最有效的方法，可以较为准确的得到系统某一时刻的位移、速度及加速度值。该类方法应用较多。微分转换法(Differential Transformation Method)[7]也是一种较为成熟的求解管路非线性振动的数值计算方法。Gu等[8]采用广义积分变换方法对两端简支载流管的动力响应进行求解。增量平衡谐波法(IHB法)因其对所研究系统非线性程度的强弱并无限制，并且方法简单求解方便，特别是其可跟踪性，在研究载流管系统的非线性幅频特性及分岔现象中存在其独有的优势[9]。

实际上，对于两端支撑载流管及悬臂载流管非线性振动，国内外已有相关方面初步的研究。在两端简支管路方面，倪樵等[10]首先研究了单频两项谐波项组合下的两端简支载流管的幅频曲线特性，并发现了幅频曲线中幅值突变这一系统不稳定现象；梁峰等[11]则通过IHB法系统性研究了两端支撑输流管管内参数共振的情况。悬臂载流管方面，Païdoussis等[12]研究了末端质量点对悬臂载流管分岔特性的影响；倪樵等[13]研究了末端线性及非线性约束下悬臂载流管的幅频特性，并发现了脉冲峰值现象。

本文在以上研究成果的基础上，基于Hamilton原理给出两端简支管路运动方程，采用Galerkin方法进行离散化处理，使用IHB法求解探讨上述两端简支边界条件下的载流直管的幅频特性。同时对管内流速μ，质量比β，非线性约束刚度K3和质量点质量Γ等对系统的幅频特性的影响进行了探讨。

1 运动微分方程及Galerkin离散

两端简支管路的运动方程可以根据Hamilton原理推导，两端简支管路模型示意图可简化为如图1所示。

图1 两端简支模型Fig.1 Schematics of simply supported pipe

图1中，v表示管内流体的流速，mmass表示集中质量点，xm表示集中质量点所处的位置，x0表示非线性约束所处的位置，ω表示管路横向振动方向。

参考Païdoussis等[14]提到的，两端支撑管路科氏力不做功，科氏力项的非保守力所做的虚功为0。为了简单起见，这里仅考虑ω方向的振动运动，无外力作用，并且非线性方面仅考虑管路轴向弯曲变形和加在管路上的非线性运动约束。

由以上假设，根据Hamilton原理，控制方程可写成如下形式

(1)

式中：T为管路系统的动能；U为管路系统的弹性势能；δ为在指定时间区间内所取的变分。

管路因轴向弯曲变形而伸长，同时产生附加的轴向应变，此轴向应变可按照下面思路进行求解：取管路的dx微元段，在此微元段上，管道的伸长量为

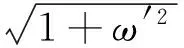
(2)

则整个管路系统的总轴向弯曲应变为

(3)

管路动能项T主要分为三部分：管道结构产生的动能、流体部分产生的动能及质量点产生的动能，其表达式如式(4)所示，仅考虑ω方向动能项：

T=Tp+Tf+Tm,

(4)

势能项如式(5)，仅考虑ω方向势能，并且考虑到因弯曲变形产生的应变

(5)

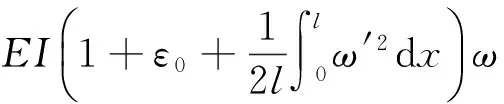
(6)

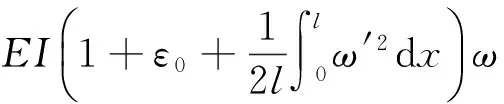
Kω3δ(x-x0)=0

(7)

式中：δ()为Dirac delta函数。

为了便于数值计算和分析比较，引入以下无量纲参变量对上式进行简化分析

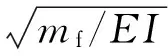
γ=EAl2/2EI，K3=Kl5/EI，

Γ=mmass/(mp+mf)l

(8)

将式(8)中的无因次量代入式(7)，可以得到如下无因次化运动微分方程

K3η3δ(ξ-ξ0)=0

(9)

式中：η‴′的系数项中后两项相比于1为一阶小量，可略去不计。

上述运动微分方程的求解可以采用Galerkin方法，为了便于求解，首先将上述无因次化的四阶偏微分方程进行离散化处理，将位置导数和时间导数分离，然后通过梁函数对位置导数进行积分，便可化简得到二阶振动常微分方程，为了简单起见，这里忽略质量点对振动方程的影响，具体实现步骤如下所示。

首先运动位移项η可以写成如下形式

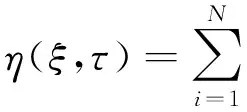
(10)

式中：ξ为管路广义坐标；φi(ξ)为梁的振型函数。该振型函数满足不同边界条件，本例中该振型函数满足两端简支边界条件，即：

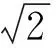
(11)

在保证计算精度的基础上，取前两项进行研究，则运动位移表达式可以写成以下形式

η(ξ,τ)=φ1(ξ)q1(τ)+φ2(ξ)q2(τ)

(12)

为了规范化及后续变形计算，上式可以写成如下矩阵形式

Φ=(φ1φ2)T，Q=(q1q2)T

η(ξ,τ)=QTΦ=ΦQT

(13)

需要说明的是Φ仅与梁的广义坐标有关，Q仅与时间项有关。将式(13)代入式(9)，并去掉弯曲刚度项前一阶小量，便可得到二阶振动常微分方程。

(1+ε0)Φ‴′TQ+

K3QTΦΦTQΦTQδ(ξ-ξ0)=0

(14)

为了得到矩阵形式，上式两端左乘Φ，得到以下形式

(1+ε0)ΦΦ‴′TQ+

K3QTΦΦTQ·ΦΦTQδ(ξ-ξ0)=0

(15)

式(15)在[0,1]上对广义坐标ξ进行积分，可以得到以下标准的非线性振动常微分方程

(16)

利用梁振型函数正交性特征

(17)

λ1，λ2为梁函数的前两阶特征值，对于两端简支梁分别为π和2π。则线性项有

K=(μ2-ε0γ)△2+△4

(18)

非线性项均为位移的三次项。K3(Q)=K3ε(Q)+K3f(Q)。

(19)

将上述矩阵代入式(16)即可得到两端简支直管的二阶非线性动力学方程组。该方程组可以用增量平衡谐波法进行求解。求解方法见文献[15]，增量平衡谐波法要求所求的解为周期性的解，限于计算资源，这里求解载流管问题均取两项谐波项，则q1和q2可以写成如下形式

q1(τ)=a1cos(ωτ)+a2cos(3ωτ)+

b1sin(ωτ)+b2sin(3ωτ)，

q2(τ)=a3cos(ωτ)+a4cos(3ωτ)+

b3sin(ωτ)+b4sin(3ωτ)

(20)

式中：ω为频率比，即振动频率与简支管基频的比值。代入式(16)，便可进行求解。在实际的求解过程中，需要选择合适的主动控制变量，这里对于两端简支载流管选择频率比ω作为主动控制变量，便可以进行迭代求解并且可以通过延续算法得到系统振动幅值-频率特性。在增量计算中设置合适的计算初值及收敛误差，便可通过牛顿迭代得到稳定解。

2 计算结果及分析

两端简支载流管计算参数选取如下：β= 0.15，ε0= 0，非线性约束位置取ξ0= 0.5，在此基础上讨论了各种参数(包括管内流速μ，质量比β，非线性约束刚度K3和质量点质量Γ等)对两端简支输流直管路的幅频特性及其他非线性特性的影响。取ξ0= 0.7处管路无因次振动幅值作为观察值，下文如无特殊说明幅值均取该处振幅。

首先是管内流速变化对系统振动幅值的影响。按照线性理论，无因次流速μ在大于3.14时管路将发生屈曲失稳，以下给出该速度范围内不同速度下的振动幅频曲线，如图2所示。

图2 不同无因次流速下管路振动的幅频特性曲线Fig.2 Amplitude-frequency curves of the pipe vibration at different dimensionless velocity

从图2中可以看到较为明显的幅值突变情形，幅值突变的幅度和流速大小有关，图中随着流速的增加，其突变的幅度逐渐增大。另外，在无因次流速在3.14～6.28内，发生幅值突变处的无因次频率比ω随着流速的增加而增大，但在6.28～9.43内，发生幅值突变处的无因次频率比ω并不遵循上述规律。这从另一方面说明在低速范围内，管路振动仍存在一定的线性因素，而在流速较大情况下，管路振动中非线性逐渐明显。

无因次流速μ大于9时管路振动存在零响应、稳

定和不稳定响应共存的情况，系统的实际响应和计算时设定的初始值有关，这里仅给出同一种初始值下的响应幅频曲线见图3。图中均存在幅值突变的情形，并且随着流速的增加，幅频特性中突变的幅度增大。

图3 μ= 8，9，10，11，12时管路振动的幅频特性曲线Fig.3 Amplitude-frequency curves of the pipe vibration at different dimensionless velocity

图4、5、6为无因次流速μ为4、8和12的管路振动的时历曲线和相图(极限环)。可以看到，在速度较低的情况(μ= 4)中，其管路振动基本上是单频的，不存在叠加情况，可见此时系统主要为线性的；而在速度较大的情况下，管路振动存在多个频率叠加，此时系统非线性因素不可忽视。

图4 μ=4时管路振动时历曲线和相图Fig.4 Time history and phase portrait for μ=4

图5 μ=8时管路振动时历曲线和相图Fig.5 Time history and phase portrait for μ=8

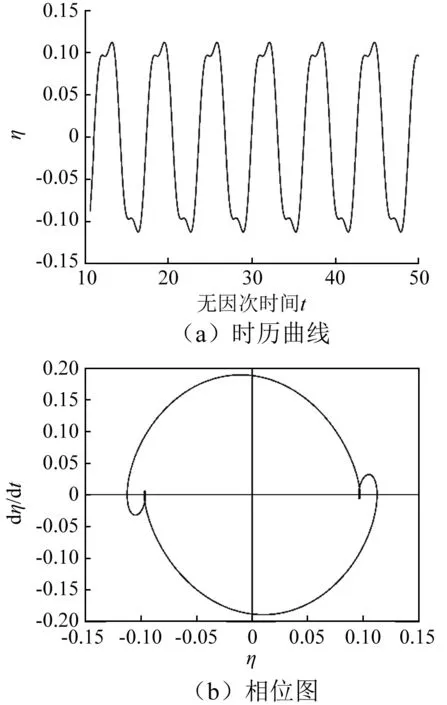
图6 μ=12时管路振动时历曲线和相图Fig.6 Time history and phase portrait for μ=12

质量比对载流管的振动幅频特性有一定的影响，并且以上不同速度区间中其影响不尽相同，图7～图10

给出了不同速度区间中不同质量比对载流管振动幅频曲线的影响关系。

图7 μ=4时不同质量比下管路振动幅频曲线Fig.7 Amplitude-frequency curves of the pipe vibration when dimensionless velocity is μ= 4

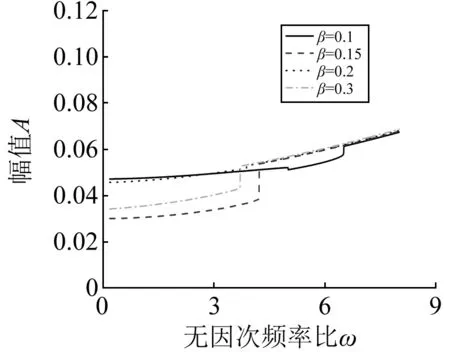
图8 μ=8时不同质量比下管路振动幅频曲线1Fig.8 Amplitude-frequency curves of the pipe vibration when dimensionless velocity is μ= 8

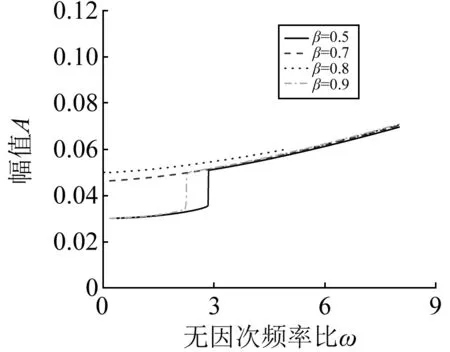
图9 μ=8时不同质量比下管路振动幅频曲线2Fig.9 Amplitude-frequency curves of the pipe vibration when dimensionless velocity is μ= 8

首先是低速段μ=4，可以看到质量比仅仅影响幅频曲线中突变处的频率比，对突变前后的幅值均无影响；对于中速段μ=8，图中可以看到质量比不仅仅影响幅频曲线中突变处的频率比，同样对突变前的幅值有很大影响，但对突变后的振幅影响较小，并且随着质量比的增大毫无规律可言；到了高速段，上述中速段的规律仍适用，同样的结论也可见于文献[10]。

前文讨论的是两端简支管路仅考虑管路沿中线的轴向变形所产生的非线性因素，当然，两端简支管的非线性不仅仅局限于此，管内不稳定流或者是非线性约束同样会引起载流管丰富的非线性振动现象。下面讨论非线性运动约束刚度对管路振动的影响。

非线性运动约束下的管路振动是管路非线性振动中一个热门的研究课题。通常而言，非线性运动约束产生的对管路的反作用力可由三次非线性弹簧来进行模拟[16]，并且可以通过该三次非线性弹簧的刚度系数来表征该运动约束的软硬程度，刚度系数越大代表运动约束越刚，反之亦然。这里，对于两端简支载流直管路，假定其非线性约束的位置在管路中间，即非线性约束位置取ξ0= 0.5，其他参数μ= 4；β= 0.15，ε0= 0，流速选择参考文献[16]。图11给出了不同非线性约束无因次刚度值对应的载流管幅频特性曲线。

图中可以很明显看到，在运动约束刚度较小的时候，即运动约束刚度在1 000以内，非线性运动约束对管路振动基本无影响，其发生振幅突变的无因次频率比均为2.23处左右，由此可见，对于运动约束无因次刚度值较小的情况，载流管振动非线性体现在其他方面(轴向弯曲变形)，运动约束对管路非线性的动力学特性基本无影响；仅改变运动约束刚度至100 000，图中可以看到不同频率比对应的振动幅值开始明显减小，说明此时运动约束和轴向弯曲变形一样在很大程度上影响了管路系统的动力学特性，这点和文献[16]通过四阶龙格库塔法计算的结论不谋而合。但本文的计算量无疑要小于龙格库塔法，这说明了增量平衡谐波法对于分析载流管非线性振动方面问题的有效性和优越性。

自由端质量点也是悬臂载流管非线性振动中一个重要的研究方向。为了简单起见，本文不考虑质量点对非线性项的作用，Galerkin离散过程与上述介绍的流程一致，且质量点位于管路上距ξ= 0.3处。

取无因次参数μ= 4；β= 0.2，不同无因次质量点质量Γ= 0，0.02，0.05，0.1，0.2，计算得到不同质量点质量的低频率比下系统的幅频特性曲线如图12所示。

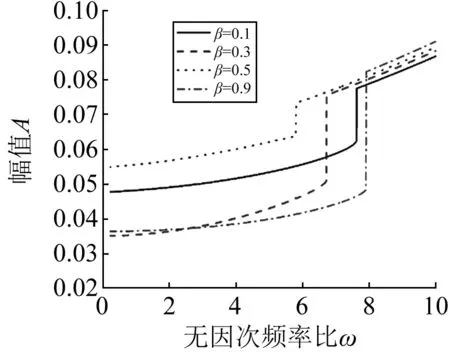
图10 μ= 10时不同质量比下管路振动幅频曲线Fig.10 Amplitude-frequency curves of the pipe vibration when dimensionless velocity is μ= 10

图11 不同非线性约束刚度值下管路幅频特性曲线Fig.11 Amplitude-frequency curves of the pipe vibration at different stiffness of nonlinear constraint

在低频率比段，上述几种不同质量的质量点对系统的幅频特性基本上影响较小；质量点对幅频曲线突变处的频率比及之后相同频率比对应的幅值有一定的影响，并且随着质量点质量的增加，突变点对应的频率比减小，同时质量点质量越大，相同频率比下振动幅值越大。

3 结 论

本文利用Hamilton原理建立了两端简支载流直管运动微分方程，经Galerkin离散，利用增量平衡谐波法，研究了两端简支载流直管路的非线性振动特性，得到以下结论：

(1)对于两端简支载流管，在临界流速以上，随着流速的增加，突变的幅度逐渐变大；无因次流速在3.14～6.28范围内，幅值突变处的无因次频率比随着流速的增加而增大。

(2)质量比及非线性约束刚度均对两端支撑管路振动幅频特性曲线产生较大影响。质量比对幅频特性曲线在不同速度区间上影响不尽相同；非线性约束刚度在刚度较低时对幅频曲线基本上无影响，而在刚度大于某一值时，振动幅值随着刚度的增加而明显减小。

(3)增量平衡谐波法能有效针对载流管非线性振动进行求解。在求解载流管非线性振动中，增量平衡谐波法不仅可以考虑系统参数中诸如流速、质量比等因素对系统非线性振动的影响，同样可以考虑管路附件例如非线性约束及集中质量点对系统非线性的影响，得到与龙格库塔积分法类似的结果，是一种较为准确及简洁的半解析、半数值计算方法。该研究可为载流管设计提供一定的参考。

[1] 周知进, 陈雄, 康红军, 等. 海流冲击对深海采矿装备液压管道流固耦合振动的影响[J]. 噪声与振动控, 2015(2)： 7-10.

ZHOU Zhijin, CHEN Xiong, KANG Hongjun, et al. Influence of ocean current inpact on fluid-structure coupled vibration of deep-sea mining equipment’s hydraulic pipelines[J]. Noise and Vibration Control, 2015(2)： 7-10.

[2] 田家林, 袁长福, 杨琳, 等. 输气管道气固耦合振动特性分析[J]. 机械科学与技术, 2016(7)： 1028-1034.

TIAN Jialin, YUAN Changfu, YNAG Lin, et al. The vibration characteristics analysis of gas and solid coupling in gas pipelines[J]. Mechanical Science and Technology for Aerospace Engineering, 2016(7): 1028-1034.

[3] LEE U, PAK C, HONG S C. The dynamics of a piping system with internal unsteady flow[J]. Journal of Sound and Vibration, 1995， 180(2): 297-311.

[4] 张立翔，黄文虎. 输流管道非线性流固耦合振动的数学建模[J].水动力学研究与进展A辑，2000, 15(1): 116-128.

ZHANG Lixiang, HUANG Wenhu. Nonlinear dynamical modeling of fluid-structure interaction of fluid-conveying pipes[J]. Journal of Hydrodynamics, Ser A, 2000, 15(1): 116-128.

[5] WADHAM GAGNON M, PAÏDOUSSIS M P, SEMLER C. Dynamics of cantilevered pipes conveying fluid. Part 1: Nonlinear equations of three-dimensional motion[J]. Journal of Fluids and Structures, 2007, 23(4): 545-567.

[6] MODARRES SADEGHI Y, PAÏDOUSSIS M P. Nonlinear dynamics of extensible fluid-conveying pipes, supported at both ends[J]. Journal of Fluids and Structures, 2009, 25(3): 535-543.

[7] KUO B, LO C. Application of the differential transformation method to the solution of a damped system with high nonlinearity[J]. Nonlinear Analysis: Theory, Methods & Applications, 2009, 70(4): 1732-1737.

[8] GU J, AN C, DUAN M, et al. Integral transform solutions of dynamic response of a clamped-clamped pipe conveying fluid[J]. Nuclear Engineering and Design, 2013, 254: 237-245.

[9] SEMLER C, GENTLEMAN W C, PAÏDOUSSIS M P. Numerical solutions of second order implicit non-linear ordinary differential equations[J]. Journal of Sound and Vibration, 1996, 195(4): 553-574.

[10] 倪樵, 黄玉盈. 增量谐波平衡法用于输液管的非线性振动分析[J]. 华中理工大学学报, 2000(10): 43-45.

NI Qiao, HUANG Yuying. Incremental harmonic balance method for nonlinear vibration of pipe conveying fluid[J]. Journal of Huazhong University of Science and Technology, 2000(10): 43-45.

[11] 梁峰, 杨晓东, 闻邦椿. 基于增量谐波平衡法的两端固定输流管参数共振[J]. 机械工程学报, 2009(7): 126-130.

LIANG Feng, YANG Xiaodong, WEN Bangchun. Parametric resonances of clamped-clamped pipes conveying fluid by incremental harmonic balance method[J]. Journal of Mechanical Engineering, 2009(7): 126-130.

[12] PAÏDOUSSIS M P, SEMLER C. Non-linear dynamics of a fluid-conveying cantilevered pipe with a small mass attached at the free end[J]. International Journal of Non-Linear Mechanics, 1998, 33(1): 15-32.

[13] 倪樵, 黄玉盈. 非线性约束粘弹性输液管的动力特性分析[J].华中科技大学学报, 2001(2): 87-89.

NI Qiao, HUANG Yuying. Dynamic analysis of restrained viscoelastic pipe conveying fluid[J]. Journal of Huazhong University of Science and Technology, 2001(2): 87-89.

[14] PAÏDOUSSIS M P, LI G X. Pipes conveying fluid: a model dynamical problem[J]. Journal of Fluids and Structures, 1993, 7(2): 137-204.

[15] CHEUNG Y K, CHEN S H, LAU S L. Application of the incremental harmonic balance method to cubic non-linearity systems[J]. Journal of Sound and Vibration, 1990, 140(2): 273-286.

[16] 王琳. 输流管道的稳定性、分岔与混沌行为研究[D]. 武汉:华中科技大学, 2006.

NonlinearvibrationofhingedpipesconveyingfluidwiththeIHBmethod

WANG Peng，ZHANG Yong’ou，WANG Sheng，ZHANG Tao

(School of Naval Architecture and Ocean Engineering, Huazhong University of Science and Technology, Wuhan 430074, China)

The nonlinear vibration of simply supported pipes conveying fluid was investigated through the incremental harmonic balance method. The differential motion equations of simply supported pipes conveying fluid were derived based on the Hamilton principle, considering the influence of the nonlinear constraint and the tip lumped masses. The equations were discretized by the Galerkin scheme. The amplitude-frequency characteristics curves of the pipes conveying fluid were obtained by changing the frequency ratio. The effect of the fluid speed, mass ratio, the stiffness of the nonlinear constraint, and the tip lumped masses on the amplitude-frequency characteristics of the pipes conveying fluid were discussed. The results show that the incremental harmonic balance method is an effective method to solve the problem of the nonlinear vibration of the pipes conveying fluid.

pipes conveying fluid；incremental harmonic balance method；nonlinear constraint；the tip lumped masses

2016-04-29 修改稿收到日期：2016-07-30

王鹏 男，硕士生，1991年生

张涛 男，博士，副教授，1976年生

O633.1

A

10.13465/j.cnki.jvs.2017.20.037