基于改进CEEMD的超声检测信号自适应降噪

孙灵芳， 徐曼菲， 朴 亨， 李 霞

(1. 吉林省节能与测控技术工程实验室， 吉林 吉林 132012； 2. 东北电力大学 自动化工程学院， 吉林 吉林 132012)

基于改进CEEMD的超声检测信号自适应降噪

孙灵芳1， 徐曼菲2， 朴 亨2， 李 霞2

(1. 吉林省节能与测控技术工程实验室， 吉林 吉林 132012； 2. 东北电力大学 自动化工程学院， 吉林 吉林 132012)

针对超声时域检测污垢数据的非平稳性和模态混叠难以实现污垢特征分离的问题，对于采用功率谱密度判定噪声区间的CEEMD分解，进而直接舍弃高频分量容易造成有效信息损失的不足，以及传统小波降噪易造成重构信号的变形等缺陷，提出基于CEEMD自相关函数的自适应软阈值降噪，引入模态自相关特性曲线判定含有噪声成分较多的IMF分量，并结合小波自适应软阈值方法拾取噪声分量中的高频有用信号。仿真分析和实验研究表明：基于CEEMD和自相关的自适应降噪方法优于传统小波阈值和单纯的CEEMD，且能很好的解决模态混叠问题，提取出污垢特征信号，对超声检测信号的处理具有重要意义。

超声检测；完备总体经验模式分解；自相关函数；自适应；降噪

换热设备中循环冷却水在水冷器的流动传热过程中，因温度和流速的变化而在换热器壁面上逐渐形成污垢，严重危害生产的安全性与经济性[1-3]。对污垢的监测、预测与抑制研究正受到各国研究者的重视。目前对污垢监测的研究普遍采用热阻法作为污垢量的间接衡量指标[4]，可信度有待提高。超声检测以其具有高效、安全、快捷等优点在实际工业生产过程中得到了广泛运用[5]。由于实际换热设备中污垢本身质软，疏松，分布不均匀且换热管道多为小径薄壁管，在检测过程中存在噪声与干扰，影响污垢特征的分析与提取。到目前为止，已有较多学者利用小波-自相关方法提取各子信号中能量较弱的特征信号[6]。Zheng等[7]针对转子实验数据高频间歇信号实行基于CEEMD的排列熵随机检测，相比单纯CEEMD保证加噪信号分解的完备性。Zhao等[8]将CEEMD运用于变速箱系统，选择IMF值作为支持向量机(SVM)分类器的特征输入，用于表征变速箱的缺陷严重程度，确定变速器故障。Xue等[9]提出基于CEEMD的快速自适应故障分解，以原始信号的标准偏差为0.1作为特征参数，能够实现滚动轴承仿真测试和振动信号的故障诊断，且计算成本相比EEMD明显降低。Perez-Ramirez等[10]针对信号被嵌入在高层次的噪音，采用CEEMD分解并结合小波变换实现了智能结构的建模、控制和状态评估中对固有频率和阻尼比的精确识别。管道污垢的超声检测因其回波复杂等众多因素困难更大，研究也鲜见报道。

由于污垢超声振动信号具有短时，突变等特点，是一种典型非平稳过程，而对换热污垢超声检测信号的降噪方法研究是污垢厚度特征提取的关键。本文针对污垢管道超声检测信号的模态混叠、降噪、信息提取等问题，提出采用基于改进完备总体平均经验模态分解(Complementary Ensemble Empirical Mode Decomposition,CEEMD)的自相关函数特性降噪方法，该方法针对噪声和有用信号分量分界点判定问题，从而实现信号的分解、自适应降噪和重构，为污垢的进一步定量分析与抑制奠定基础。

1 方法分析

1.1 集合经验模态分解理论

完备总体平均经验模态分解是在经验模式分解基础上发展起来的信号分解方法，EMD(Empirical Mode Decompositio)本质是对原始信号采用不同尺度分解出固有模态函数和残差[11]，然而EMD分解不稳定，存在模态混叠现象[12]，文献[13-14]中将噪声辅助分析方法应用于EMD中，提出了总体平均经验模态分解EEMD，利用高斯白噪声频谱均匀分布统计特性加至信号中，使得信号在不同尺度上具有连续性，算法步骤简述如下：

步骤1 在原始信号x(t)中多次加入0均值，标准差为常数的高斯白噪声ni(t)，此时有

r(t)i=x(t)+ni(t)，i=1

(1)

步骤2 对ri(t)进行EEMD分解，得到IMF分量imfij和残差res；

步骤3 重复步骤1和2各N次，对对应分量进行均值运算，消除多次加入的高斯白噪声影响最终得到模态分量

(2)

1.2 完备总体经验模态分解理论

EEMD 的核心思想在于把添加了高斯白噪声的原始信号 EMD后得到的模态进行加总平均，该算法虽解决了模态混叠问题，但由于引入了辅助噪声，IMF的总和并不能完美的重构原始信号。Torre等[15]提出了一种 EEMD的改进算法，即加入正负对形式的辅助噪声，以消除重构信号中的残余辅助噪声。具体步骤：

步骤1 确定阈值参数S以及加总平均次数NR，最大迭代次数MaxITer；

步骤2 向原始信号添加n组正负互补的辅助噪声，生成添加后的信号：

(3)

式中：S为原始信号，Ni为辅助噪声，Mi1、Mi2为添加噪声后的信号对，得到2n个添加了噪声的信号。

步骤3 根据：对每个添加噪声的信号利用CEEMD进行分解，每个信号得到一组IMF模态分量，将第i个信号的第j个分量表示为imfij;

步骤4 通过组合的多组分量获得分解结果：

(4)

式中：imfj表示CEEMD最终分解得到的第j个IMF分量，将信号不同尺度的波动或趋势逐级分解为一系列具有不同特征尺度的序列。

步骤5 重复步骤3和4，采用收敛判定条件为标准差系数SD，其定义如下：

(5)

步骤6 根据噪声各能量与平均周期之积为常数，确定噪声和有用信号分量分界点，直接将噪声分量剔除，并对分解后的imfj进行重构得到

(6)

2 改进CEEMD自适应消噪

含噪信号得到分解后的模态分量具有有限个频率从高到低的IMF，其中阶数小的IMF对应于信号的高频部分或噪声，阶数大的对应于信号的低频成分或有用信号。随机信号的自相关函数是信号时域特性的一种平均度量，反映了信号在不同时刻取值的相关程度[16]。假定原信号x(t)为随机信号，其自定义相关函数迭代形式为

(7)

式中：T为信号周期，τ为时延。

取采样频率为50，采样间隔为0.02 s时随机噪声和一般信号的自相关函数，并进行归一化得到结果如图1。

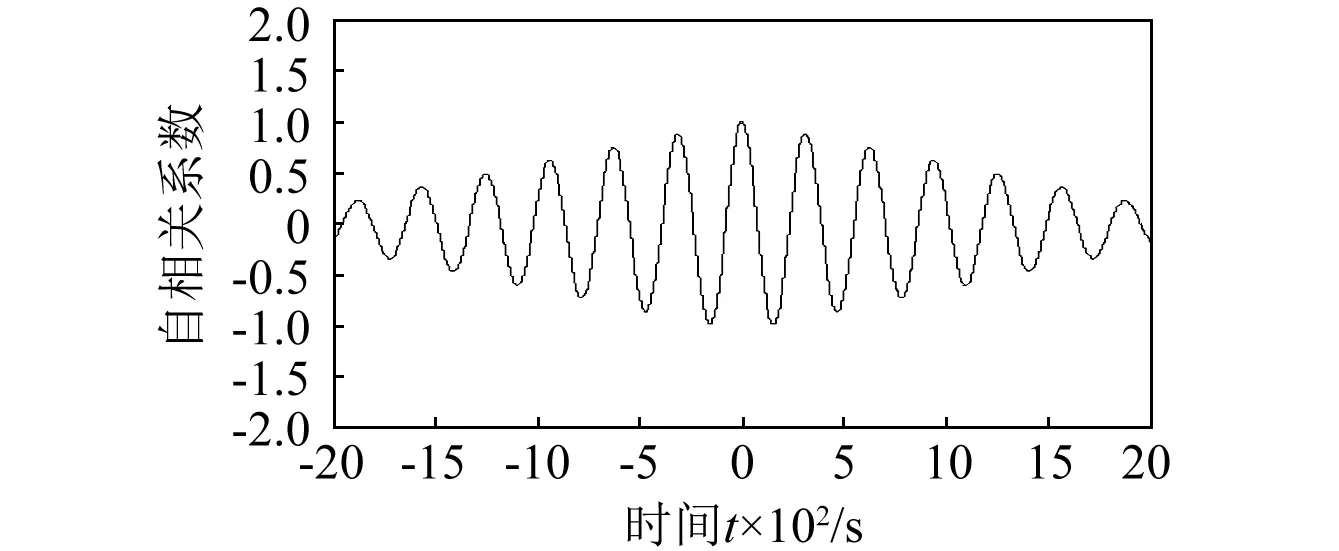
(a)随机函数自相关

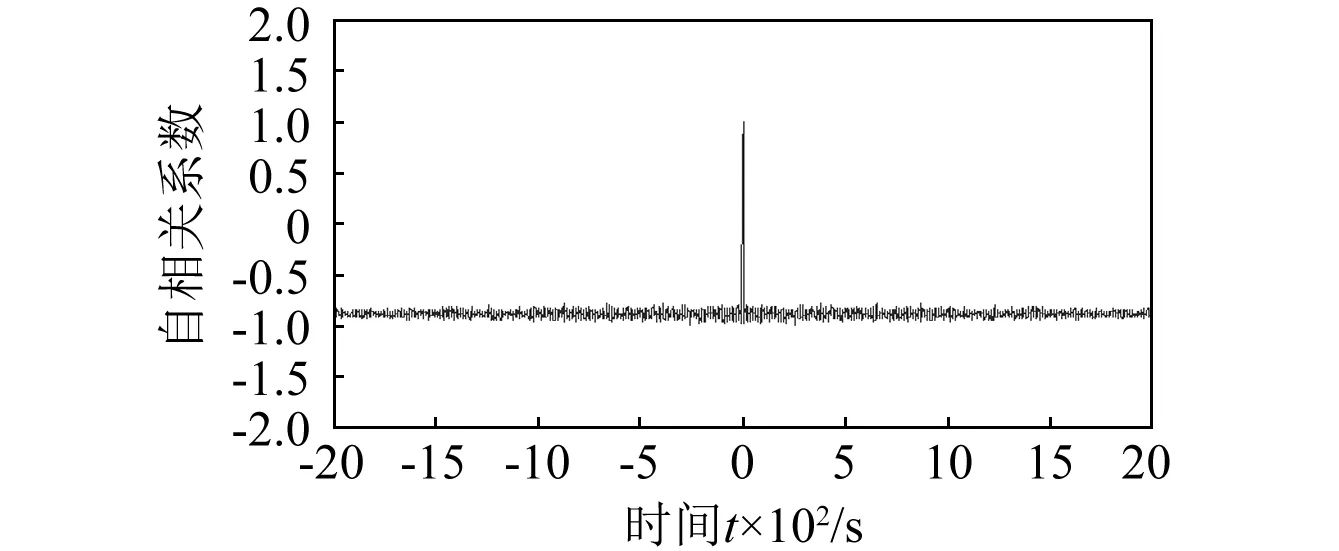
(b)噪声自相关图1 仿真信号自相关波形Fig.1 Autocorrelation waveform of simulation signal

对于随机噪声函数，由于其各时刻的弱相关性及随机性，导致其在零点相关性最强，而其他位置的相关性非常弱，体现在波形方面，即为在其他位置迅速衰减为0。理想情况下的高斯白噪声，则会出现它的归一化函数值在零点处为一，在其他点处为零的现象。而对于一般信号而言，其自相关函数也是在零点处取得最大值，但由于信号间关联特性的缘故，自相关函数在其他点处并没有迅速衰减到一个很小的值，而是逐渐衰减，这有别于噪声的自相关函数变化情况。而针对CEEMD分解后的尺度模态IMF分量判定高频分量分界点K，并拾取在高频信号的有用信号，实行自适应降噪，将有用信号与低频IMF进行叠加，重构出有效信号。阈值选取规则按以下式子进行估计[17]

(8)

此时可利用结合自相关函数后的自适应去噪IMF分量和趋势项，重构原信号即可得到降噪后的信号

(9)

3 仿真分析

为更好实现对降噪方法的定量评价，本文模拟仿真了超声回波类信号，并进行降噪实验以观察算法效果，由于由高斯窗函数调制形成的Gabor原子在时、频域均有较好局部特性[18]，因此本文采用Gabor原子仿真超声回波信号，此处将一个Gabor型衰减振荡信号与含有三个强度不一脉冲的时域序列进行卷积，以模拟超声信号通过三层不同介质交界后产生的无噪超声回波信号。对模拟声道的三个脉冲，取脉冲幅度分别为1.7、0.75和1.3，保证幅度比3:1:2，以模拟超声检测中由于介质的物理性质差异而产生的回波强度不同，也更有利于在后续实验中对降噪方法的信号细节保护能力进行对比检验，以信噪比SNR和互相关系数RMSE作为评判标准。

在仿真信号中加入高斯白噪声，信噪比为10 dB，对加噪信号采用传统小波硬阈值与小波软阈值，小波降噪采用‘sym6’原子进行5层小波分解，阈值选取规则采用‘rigrsure’无偏似然估计，结果如图2所示。

图2显示当原信号噪声干扰较小时，小波硬阈值与小波软阈值降噪均发生了一定变形，此时降噪后硬阈值平均信噪比SNR=11.279 8，均方根误差RMSE=0.084 2，软阈值SNR=12.368 4，RMSE=0.079 2，传统小波降噪对信号的损失较大。

采用原始EEMD进行分解如图3，噪声实现数为500组，迭代上限为5 000，SD=0.2，由图3观察由于噪声信号干扰，在前3阶模态分量中，出现了模态混叠，并且产生了较多的虚假分量，根据巴赛瓦等式

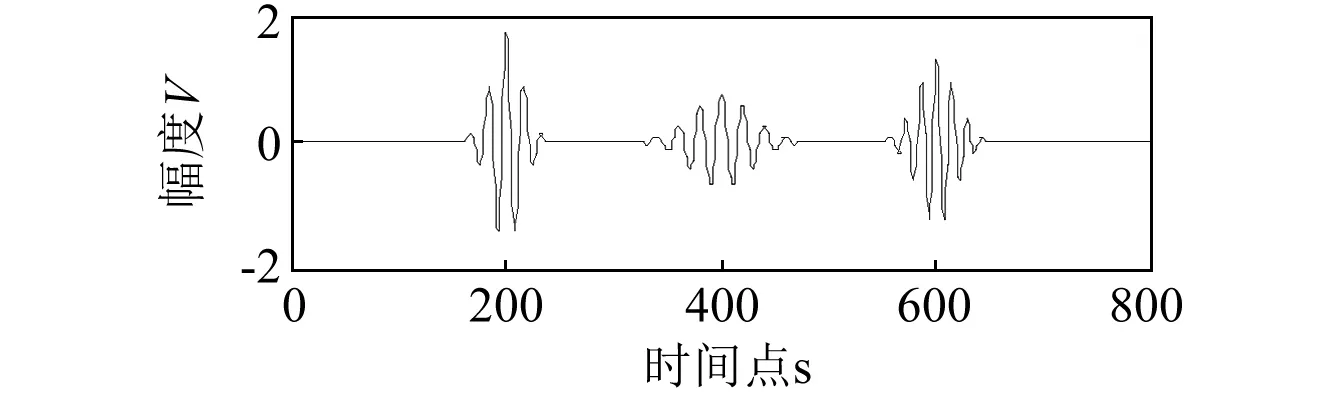
(a)参考信号

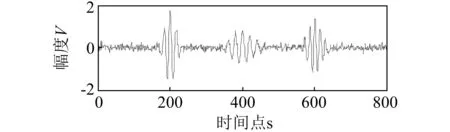
(b)加噪信号

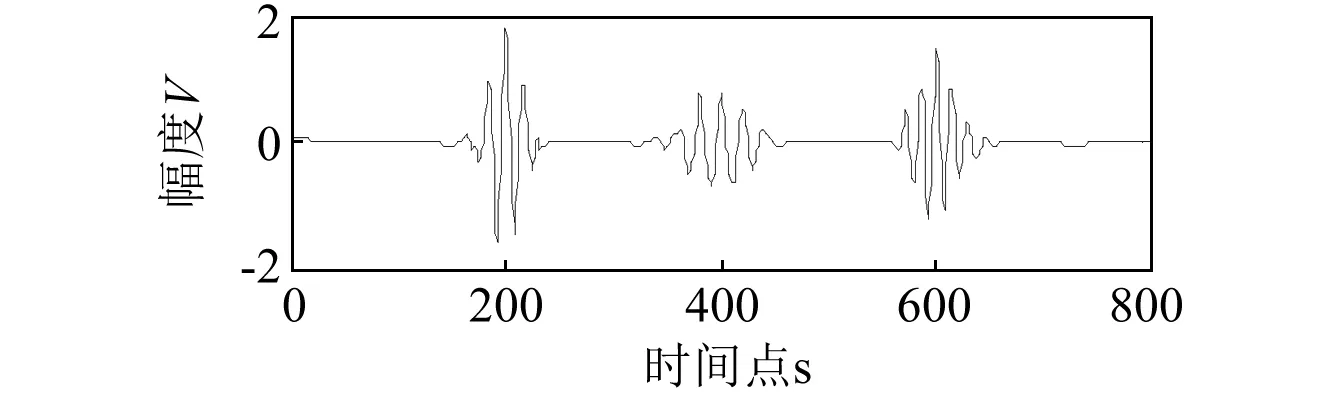
(c)DWT硬阈值

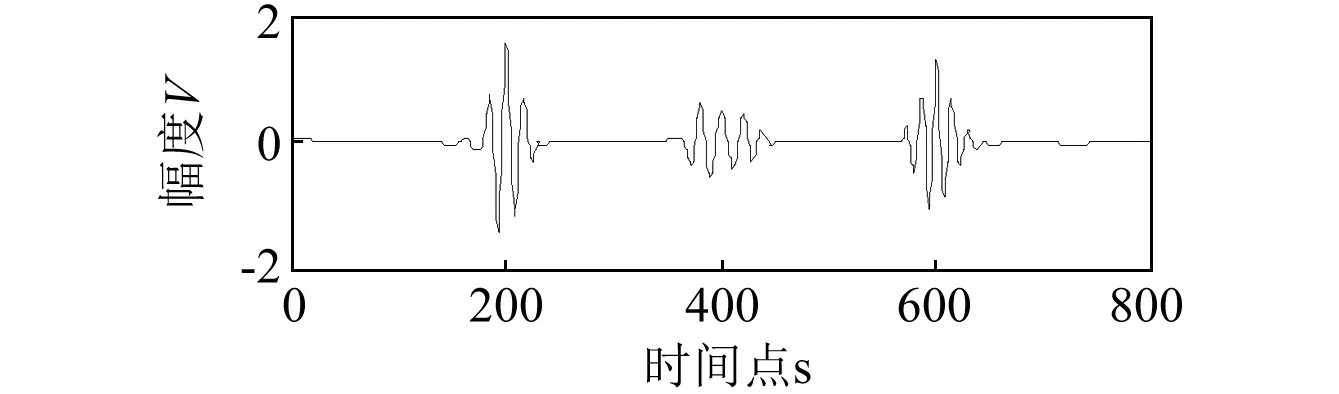
(d)DWT软阈值图2 超声仿真信号降噪结果(SNR=10 dB)Fig.2 Ultrasonic simulation signal denoising results(SNR=10 dB) [f(t)]2dt=|F(w)2|dw

(10)

求得不同模态分量的包络谱，选取前四阶如图4(a)～(d)。

图3 仿真信号EEMD分解结果Fig.3 EEMD decomposition of the simulation signal

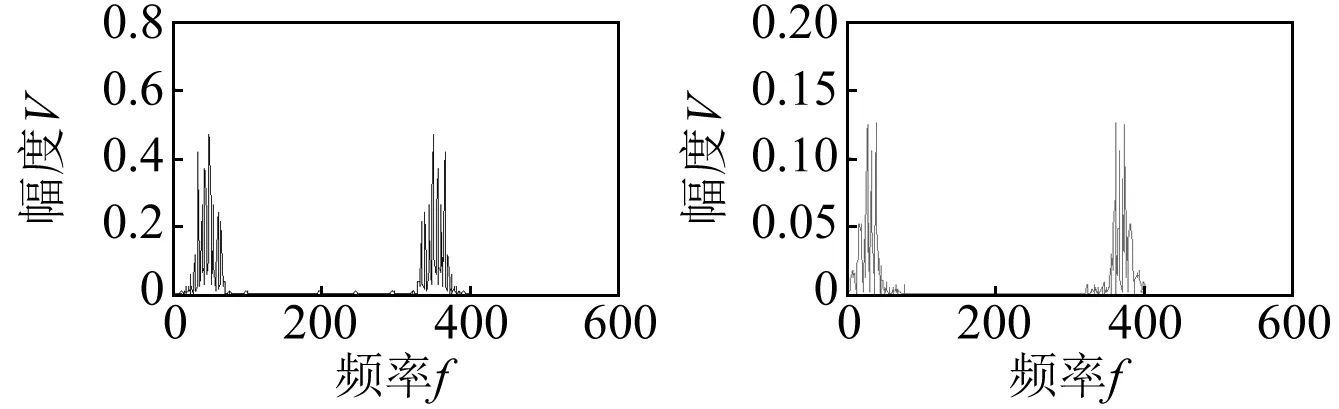
(a)IMF1包络谱 (b)IMF2包络谱

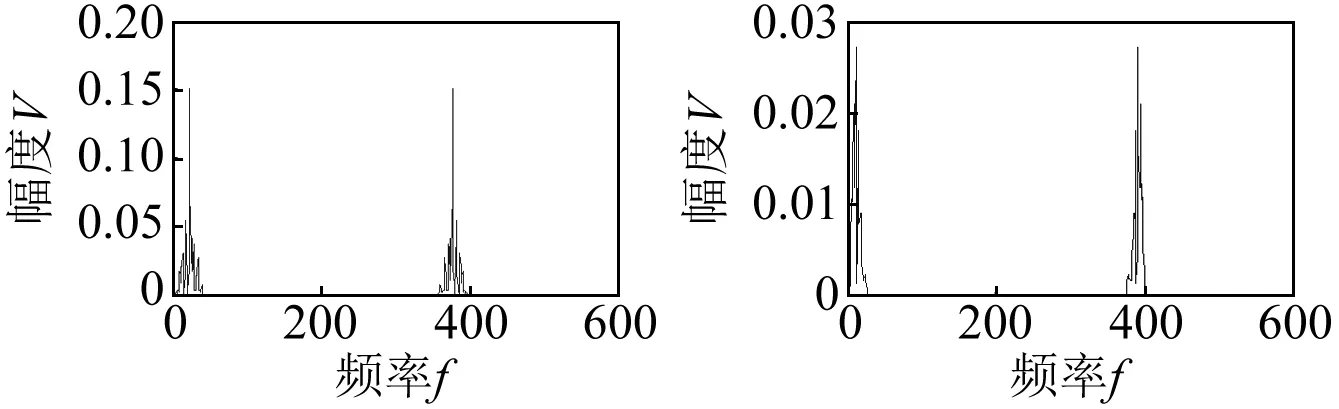
(c)IMF2包络谱 (d)IMF4包络谱

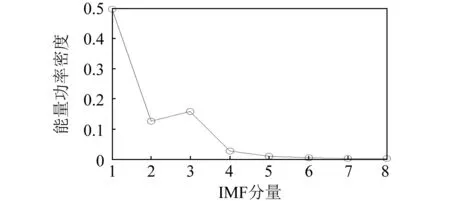
(e)EEMD分解IMF分量功率密度统计结果图4 包络谱能量分布Fig.4 The energy distribution of envelope spectrum

由图4(a)～图4(d)可见，分布在各阶IMF上采样点逐渐向低能量段集中，噪声总能量呈递减趋势。由于噪声频段一般较高，当有用信号出现时，往往会打破递减趋势，产生一个局部的能量分布极大值点，该极值点之后，信号将替代噪声成为各级模态的能量主导。第一个局部极大值对应的阶数为3，因此重构第3个及以后的所有IMF分量，得到去噪后结果如图5所示。

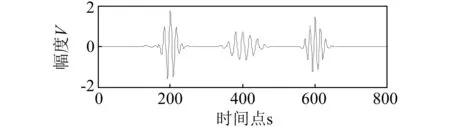
图5 原始EEMD降噪结果Fig.5 The denoising results of EEMD

此时图5中对应的SNR=13.800 4，RMSE=0.056 6，信噪比相比传统的小波硬阈值与软阈值都有了较大提升，但在去除噪声时，波形也产生了变形，在原信号幅值0处部分变形较为明显。尽管集合经验模态分解方法可以提供合理的分解结果，并且平滑效果突出，获得了较好的降噪效果，但由于引入了辅助噪声，IMF的总和并不能完美的重构污垢管道回波信号。

针对改进后的CEEMD降噪算法(加总平均次数为1 000)得到分解后的10阶模态分量以及各阶模态的自相关函数，分别如图6、图7所示。

图6 改进CEEMD分解结果Fig.6 The modified CEEMD decomposition results

图7 模态分量自相关函数波形Fig.7 Autocorrelation waveform of IMF

观察图6可知，污垢管道回波仿真信号中含有大量的随机噪声和高频噪声干扰成分，采用CEEMD分解后的各模态分量在IMF1～IMF5阶有用信号淹没在噪声中，而结合图7，可以判断出噪声分量与有用信号的分界点K，对应的各模态分量的自相关函数波形由零点处集中向两周扩散，和理论分析一致。此时k=5，对IMF1～IMF5实行自适应软阈值降噪，根据计算各模态分量的中值，可获得降噪后的模态分量，对其进行重构可得到图8。

本文算法所得重构污垢管道回波仿真信号的SNR=14.696 5，RMSE=0.041 0，相比传统小波和原始EEMD和CEEMD分解可以在有效去除噪声的同时，较好的保留信号细节，且信号没有发生形变，去噪效果从视觉效果和定量研究上而言优于其他两种传统算法。

为了更好的分析本文算法的有效性，调整信号强度，针对噪声强度较大信噪比为-3 dB时，可获得上述几种信号降噪方法对污垢管道回波仿真处理结果，如图9所示。

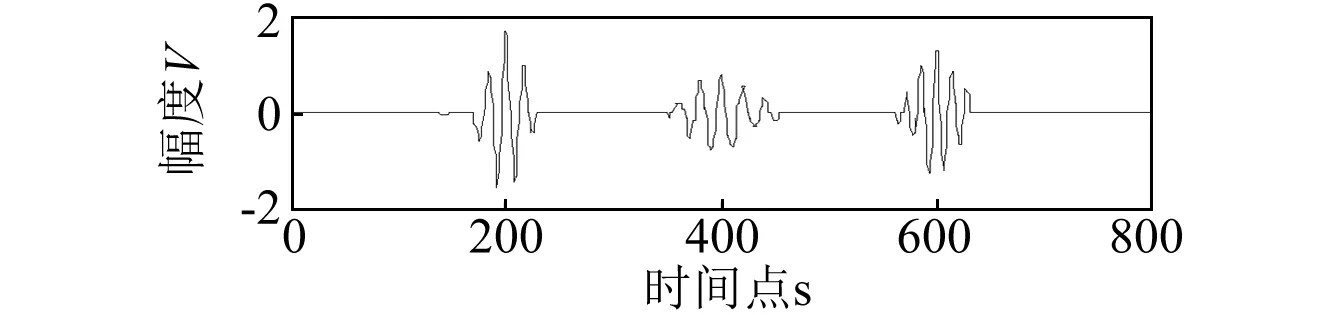
(a)原始CEEMD方法

(b)本文研究方法图8 仿真信号降噪结果Fig.8 Denising result of simulation signal

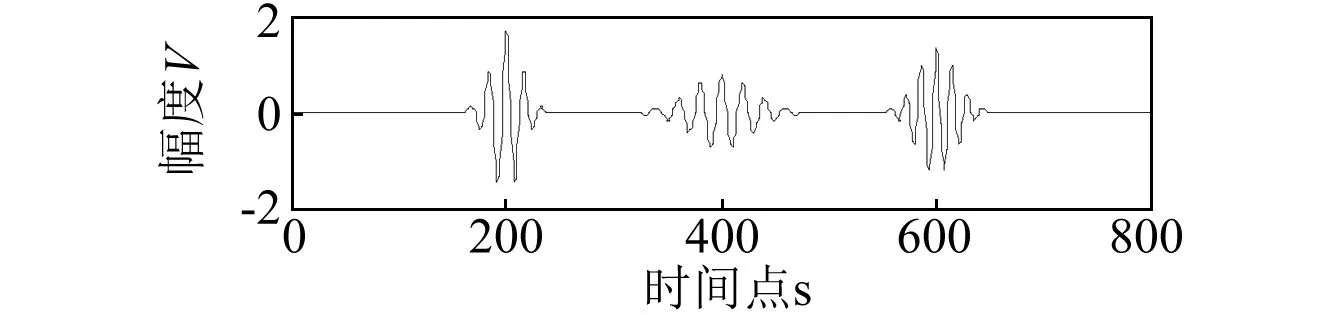
(a)参考信号

(b)加噪信号

(c)DWT硬阈值

(d)DWT软阈值

(e)CEEMD方法

(f)本文研究方法图9 仿真信号超声降噪结果(SNR=-3 dB)Fig.9 Ultrasonic simulation signal denoising results(SNR=-3 dB)

当信噪比为-3 dB时，几种方法都能有效的实现污垢管道回波降噪，由图9(b)可见，噪声几乎淹没了污垢特征回波，小波硬阈值与软阈值波形都发生了严重变形，且平滑效果差，而采用原始CEEMD算法变形程度较传统小波降噪较小，波形较为平滑，但在幅值为0处仍有较多毛刺，而经自相关函数的完备总体经验模态自适应降噪结果在保存有效污垢管道回波信号的基础上能够实现进一步的去噪，且平滑效果更清晰。以上实验较直观的对CEEMD等方法的降噪结果进行了比较和分析，为了更好的对降噪结果进行定量分析，分别以上述降噪方法进行多次降噪实验，将原含噪信号及其降噪后的信噪比和均方根误差进行平均，绘图于图10，并将降噪结果统计于表1中。

图10 降噪效果示意图Fig.10 Schematic diagram of denoising effect

4 实验信号处理

本课题组拟用超声时域反射法开展换热设备污垢管道直接监测研究，实验基于换热设备污垢动态模拟装置[19]，实验台使经冷却的工质匀速通过处于恒温水浴箱中铜管，并进行循环。换热管外侧水浴温度设置为50 ℃，工质冷却温度设定为30 ℃，铜管径25 mm，壁厚1.5 mm。采用OLYMPUS 5072PR型手动控制脉冲发生接收器，选用YOKOGAWA SL1000数据采集系统，对逐渐生成的管道污垢进行超声检测实验，在对换热管道进行彻底清洗后，将去离子水和化学试剂反应生成的碳酸钙饱和水溶液作为介质投入换热循环以生成污垢，并以万向架架设超声探头于工作管上方对管内污垢进行检测。按污垢生长的一般规律，选择污垢生长可能进入稳定状态的时间作为污垢生成动态模拟实验的进行时间，一般选择每组实验持续时间为15天左右。管道污垢回波如图11。

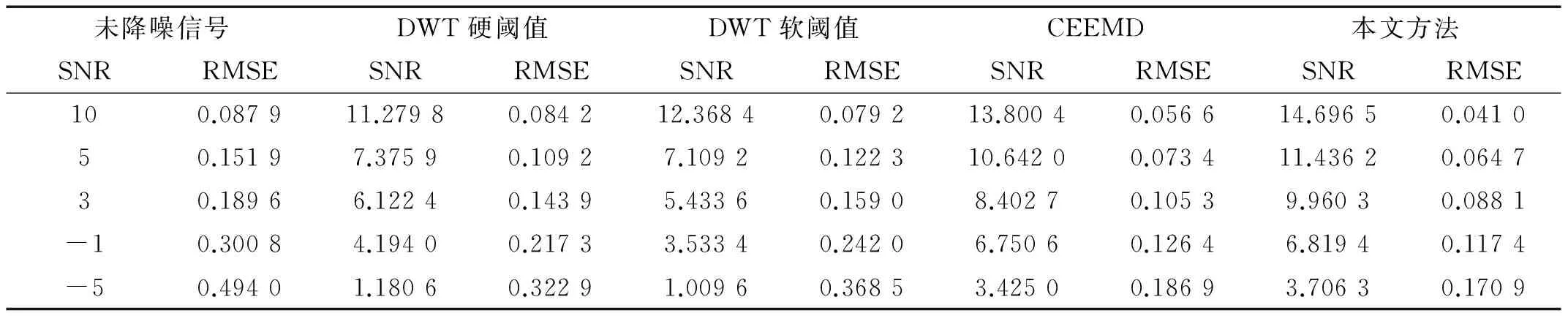
表1 降噪结果统计表Tab.1 Statistics of denoising results

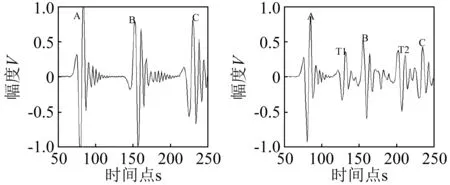
(a)清洁管道回波信号 (b)含垢管道回波信号图11 污垢管道超声回波信号Fig.11 Ultrasonic echo waveform of exchanger pipes with fouling

经过持续监测与实验，在投入运行初期，污垢生成速度较慢，无法检测到污垢回波信号，说明由于此时运行时间尚短，污垢生长尚处于诱导期内，暂无明显污垢形成。图11(a)中波形A为管道外壁回波，幅值较大，A、B、C 3个等间隔出现的集中波形为第一次第二次和第三次管道回波。图11(b)中，在第一个与第二个管道外壁回波间等间隔出现的集中波形为污垢与水层界面的一次回波，在内壁的二次与三次回波间出现的第二次集中回波波形为污垢与水层界面二次回波，此时波形A的形状发生了较明显的变形，其右侧旁瓣附近出现了幅值增大的现象，表明管内壁已形成污垢生长的初始环境，B、C在幅值上也呈现振荡衰减并伴有模态混叠现象，针对此问题可采取前文所提出的针对高混叠换热污垢超声检测信号的基于改进自相关CEEMD自适应消噪方法，提取出污垢特征回波信号分别采用EEMD和改进CEEMD对上述信号进行分解如图12(a)，噪声实现数为1 000组，迭代上限为5 000，SD=0.2，取前6阶模态分量的自相关函数并进行归一化，如图12(b)所示。

经过CEEMD分解后得到9个模态分量，能量主要集中在前4个IMF分量，其中管道污垢的简谐波成分已经被完全提取出来，解决了实际污垢管道信号的模态混叠问题，由图12(b)，其中提取了前6阶模态的自相关函数波形，观察得到在4阶以前，在零值点处能量集中，且为最大，其他位置迅速衰减为0，由此可判断此时临界点k=4，对其前4阶进行自适应软阈值去噪，并且重构得到如图13所示。

(a)超声回波改进CEEMD分解

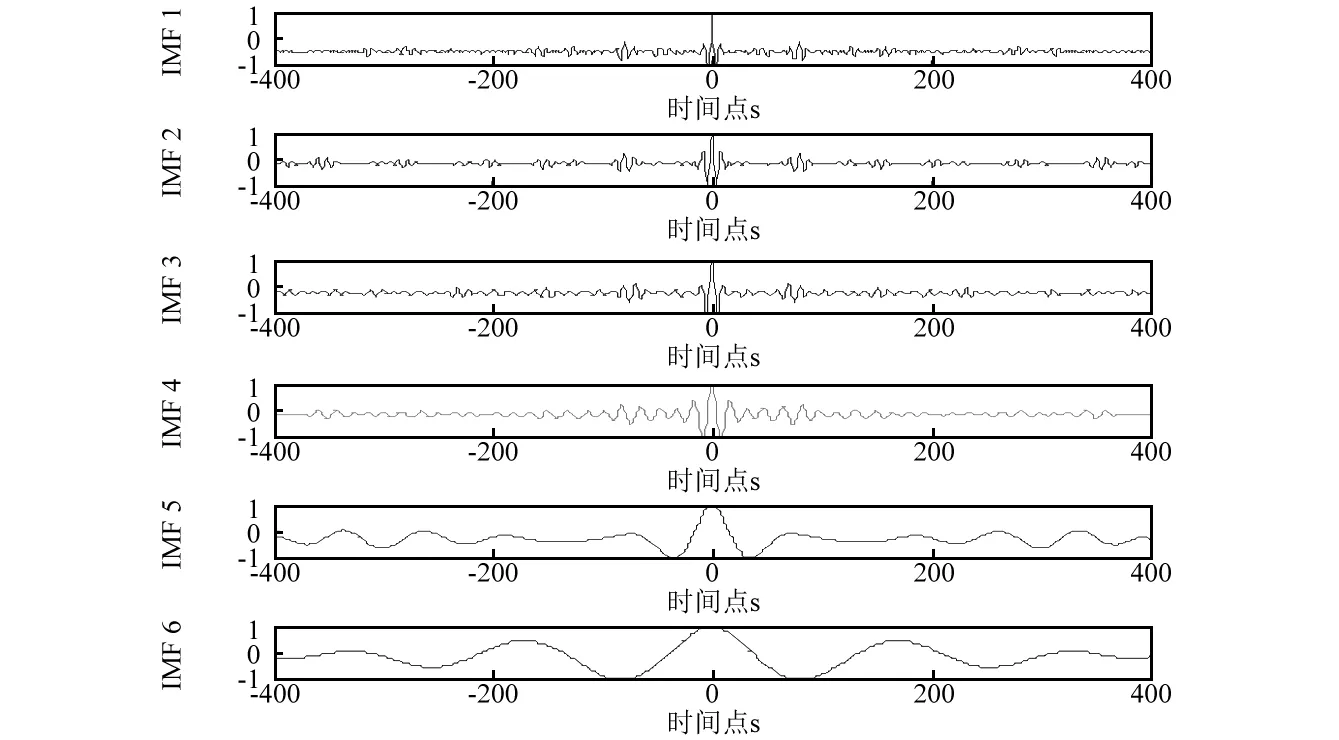
(b)前6阶CEEMD自相关函数波形图12 污垢管道振动信号分析Fig.12 The analysis of vibration signals with fouling pipes

从图13(a)可以看出原始CEEMD的降噪效果平滑性能较好，能将污垢微弱特征信号提取出来，但细节保留程度略差，而本文所采用的基于自相关函数的CEEMD自适应软阈值降噪后的重构信号较好保留了超声检测回波信号的主要信息，抑制了EMD分解过程中的模态混淆，且平滑性很好，对噪声去除更为彻底。表明改进的CEEMD算法能够较好实现污垢管道超声检测信号降噪和有效信息提取。

(a)原始CEEMD (b)本文研究方法图13 污垢管道回波降噪结果Fig.13 The denosing results of echo signal with fouling pipes

5 结 论

(1)针对换热设备污垢管道超声检测信号中的噪声和模态混叠问题，采用传统小波去噪和原始EEMD分解，直接根据能量密度谱判定模态分解区间，不能较好实现信号重构和噪声的消除。

(2)提出基于CEEMD理论的污垢管道超声检测信号特征提取，结合模态自相关的迭代方法进行含噪区间的判定，并对其中高频和干扰进行自适应软阈值降噪，有效解决了污垢回波信号在时域内的相互交错、叠加导致污垢特征信号被淹没的问题，实现了管道与污垢界面、污垢与水层界面的特征分离，比传统小波和CEEMD分解降噪结果更显著、单一，具有较高的工程应用价值。

[1] 杨善让, 徐志明, 孙灵芳. 换热设备污垢与对策[M]. 2版. 北京: 科学出版社,2004: 8.

[2] 徐志明, 张仲彬,李煜, 等.水质对板式换热器结垢的影响权重及其机制分析[J].中国电机工程学报, 2012,32(32): 69-74.

XU Zhiming, ZHANG Zhongbin, LI Yu, et al. Influences of water quality’s effect weights and mechanisms on fouling of plate heat exchangers[J]. Proceedings of the CSEE,2012,32(32): 69-74.

[3] 王建国，刘高生，孙伟. 电磁场作用下循环水污垢热阻的灰色预测模型实验研究[J].中国电机工程学报,2013, 33(11): 61-64.

WANG Jianguo, LIU Gaosheng, SUN Wei. Experiment research on fouling resistance grey forecast model for circulating water in electromagnetic field[J]. Proceedings of the CSEE,2013,33(11): 61-64.

[4] 李霞, 孙灵芳, 杨明. 基于改进FOA匹配追踪的超声信号处理研究[J].仪器仪表学报,2013,34(9): 2068-2073.

LI Xia, SUN Lingfang, YANG Ming. Research on ultrasonic signal processing based on improved FOA matching pursuit[J].Chinese Journal of Scientifi Instrument,2013,34(9): 2068-2073.

[5] 赵波, 杨善让, 刘范, 等. 冷却水污垢热阻预测的支持向量机算法动态模拟实验研究[J].中国电机工程学报,2010,30(11): 92-97.

ZHAO Bo, YANG Shanrang, LIU Fan, et al. Experimental study on dynamic simulation of cooling water fouling resistance prediction by support vector machine[J]. Proceedings of the CSEE, 2010, 30(11): 92-97.

[6] 明安波, 褚福磊, 张炜. 滚动轴承复合故障特征分离小波-频谱自相关方法[J].机械工程学报,2013,49(3): 81-86.

MING Anbo, CHU Fulei, ZHANG Wei. Compounnd fault features separation of rolling element bearing based on the wavelet decomposition and spectrum auto-correlation[J].2013,49(3): 81-86.

[7] ZHENG J D, CHENG J S, YU Y. Partly ensemble empirical mode decomposition: an improved noise-assisted method for eliminating mode mixing[J].Signal Processing, 2014,96:362-374.

[8] ZHAO L Y,YU W,YAN R Q. Gearbox fault diagnosis using complementary ensemble empirical mode decomposition and permutation entropy[J]. Shock and Vibration , 2016(1)： 1-8.

[9] XUE X M, ZHOU J Z, XU Y H, et al. An adaptively fast ensemble empirical mode decomposition method and its applications to rolling element bearing fault diagnosis[J]. Mechanical Systems and Signal Processing, 2015,62/63:444-459.

[10] PEREZ-RAMIREZ C A, AMEZQUITA-SANCHEZ J P, ADELI H, et al. New methodology for modal parameters identification of smart civil structures using ambient vibrations and synchrosqueezed wavelet transform[J]. Engineering Applications of Artificial Intelligence, 2016, 48: 1-12.

[11] 焦敬品, 张强, 何存富, 等. 机械结构液体层厚度超声谐振的测量方法[J].振动、测试与诊断,2012,32(2): 292-300.

JIAO Jingpin, ZHANG Qiang, HE Cunfu, et al. Thickness measurement of liquid layer in mechanical structure using ultrasonic resonant technique[J].Journal of Vibration, Measurement & Diagnosis, 2012,32(2): 292-300.

[12] 郑近德, 程军圣, 杨宇. 改进的 EEMD 算法及其应用研究[J]. 振动与冲击, 2013, 32(21): 21-26.

ZHENG Jinde, CHENG Junsheng, YANG Yu. Modified EEMD algorithm and its applications[J].Journal of Vibration and Shock,2013,32(21): 21 -26.

[13] 姜绍飞, 陈志刚, 沈清华, 等. 基于EEMD与FastICA的损伤异常识别与定位[J].振动与冲击,2016,35(1): 204-209.

JIANG Shaofei, CHEN Zhigang, SHEN Qinghua, et al. Damage detection and locating based on EEMD-FastICA[J].Journal of Vibration and Shock,2016,35(1): 204-209.

[14] ZHAO H W, HUANG N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2011, 1(1): 1-41.

[15] TORRES M E, COLOMINAS M A, SCHLOTTHAUER G, et al. A complete ensemble empirical mode decomposition with adaptive noise[J]. IEEE International Conference on Acoustics, 2011,125(3): 4144-4147.

[16] 余发军, 周凤星. 基于EEMD和自相关函数特性的自适应降噪方法[J].计算机应用研究,2015,32(1): 207-209.

YU Fajun, ZHOU Fengxing. Adaptive de-noising method based on EEMD and autocorrelation function property[J].Application Researchof Computer, 2015,32(1): 207-209.

[17] 刘莹, 韩炎, 郭亚丽, 等. 基于CEEMD的爆破振动自适应去噪[J].科学技术与工程, 2015,15(32): 1671-1815.

LIU Ying, HAN Yan, GUO Yali, et al. Adaptive de-noising of vibration signal based on CEEMD auto-correlation properties[J].Science Technology and Engineering,2015,15(32): 1671-1815.

[18] 李霞，杨明，孙灵芳.基于波原子理论的超声检测信号降噪方法[J].振动、测试与诊断,2014,34(1): 97-101.

LI Xia, YANG Ming, SUN Lingfang. Ultrasonic detection signal denoising based on the theory of wave atoms[J].Journal of Vibration,Measurement & Diagnosis,2014,34(1): 97-101.

[19] 李霞,孙灵芳,杨明,等.薄层污垢超声检测信号处理方法[J]. 振动、测试与诊断,2013,33(6): 961-964.

LI Xia, SUN Lingfang, YANG Ming, et al. Thin fouling ultrasonic testing signal analysis and dentification method[J]. Journal of Vibration,Measurement & Diagnosis,2013,33(6): 961-964.

Self-adaptivenoisedenoisingforultrasonicdetectionsignalbasedonimprovedCEEMD

SUN Lingfang1, XU Manfei2, PIAO Heng2, LI Xia2

(1. Energy Conservation & Measure-Control Technology Engineering Laboratory, Jinlin 132012, China;2. School of Automation Engineering, Northeast Dianli University, Jilin 132012, China)

The paper aims to detect the non-stationary of fouling data and modal aliasing which may make it difficult to realize dirt characteristic separation of ultrasonic in the time domain. As for deficiencies such as insufficient effective information loss caused by directly application of power spectral density in determination of CEEMD decomposition of noise interval as well as deformation of reconstructed signal caused by traditional wavelet denoising, self-adaptive soft threshold noise reduction of autocorrelation function based on CEEMD as well as modal correlated characteristic curve were introduced to determine the IMF component with higher noise contribution. Besides, the method of wavelet self-adaptive soft-threshold value was also applied to collect useful high-frequency signal in noise component. According to the results of simulated analysis and experimental research, the self-adaptive noise reduction method based on CEEMD and autocorrelation is more effective than traditional wavelet threshold and pure CEEMD. It can better solve the problem of modal aliasing and extract dirt characteristic signal, which is of great importance to the processing of ultrasonic detection signal.

ultrasonic detection; complementary ensemble mode decomposition(CEEMD); auto-correlation function; adaptive; denoising

国家自然科学基金(51176028);吉林省科技发展计划项目(20140204030SF)

2016-04-08 修改稿收到日期： 2016-08-16

孙灵芳 男，博士，教授,1970年生

徐曼菲 女，硕士生,1991年生

TB53

A

10.13465/j.cnki.jvs.2017.20.034