机载导弹安全分离评估方法研究
2017-11-04王慧哲王晓鹏郭宇恒
王慧哲,李 响,王晓鹏,郭宇恒
(1.北京理工大学 宇航学院,北京 100081; 2.上海机电工程研究所,上海 201109)
机载导弹安全分离评估方法研究
王慧哲1,李 响1,王晓鹏2,郭宇恒1
(1.北京理工大学 宇航学院,北京 100081; 2.上海机电工程研究所,上海 201109)
为高效地判断导弹从载机分离过程的安全性,根据分离过程中导弹和载机的相对运动关系推导了判定载机-导弹分离是否安全的Schoch判据。采用“自由流模型+干扰模型”的气动建模方法,建立起了分离过程中的导弹气动模型。在此基础上,计算得到了分离过程中导弹相对于载机运动的相对速度和相对加速度,将这些参数代入Schoch判据中,进行分离的安全性评估。采用上述方法,对某三角翼载机外挂导弹分离过程进行了分离安全性评估,验证了本方法的可行性。
导弹; 载机; 分离; 相对运动; 气动建模; 安全分离判定准则; 相对速度; 相对加速度
0 引言
从飞机上投放导弹时,需确保分离的安全性,其中对分离的安全性进行评估是一项重要内容,对此进行了大量的研究。文献[1]对机载导弹分离过程中涉及的气动、轨迹、安全性评估等进行了全面分析。文献[2]给出了评估分离的安全性性能的Schoch判据的数学表达式。文献[3]用蒙特卡罗打靶法获取大量的分离轨迹,用机器学习与数据挖掘方法研究了分离过程中的统计学规律。在国外的上述研究中,Schoch判据简洁实用,获得了较广泛的应用,关于分离安全性评估的研究一般都是基于Schoch判据展开的。在国内,文献[4]给出了安全、不安全两种分离品质,并给出了相应的评估原则;文献[5]分析了典型外挂物在不同速度、高度、姿态下投放的运动轨迹,讨论了对安全投放有重要影响的因素,提出了减少外挂物投放风险的建议;文献[6]对飞机外挂物投放过程进行数值模拟,提出了“安全线”的概念,分析了不同弹射力作用方式对外挂物投放安全性设计的影响。但在国内目前还未见关于Schoch判据的相关报道。本文对用Schoch判据对机载导弹安全分离评估进行了研究。在Schoch判据中,计算导弹的分离轨迹是重要的一步,目前一般是将CFD数据或风洞试验数据嵌入分离轨迹计算,此法精度高但计算量大耗时多[7-8]。文献[9]引入了“自由流模型+扰动模型”气动建模方法,用该法建立了分离过程中导弹气动系数的解析表达式,由该解析气动模型解算分离轨迹,既能在保证精度的前提下大幅提高计算效率,又可快速得到分离的判定结果,非常适于工程应用。本文基于对导弹与载机相对运动的分析,对Schoch判据进行了推导,并对其无量纲化,给出了通用的机载导弹分离过程安全性判定准则,同时采用“自由流模型+扰动模型”气动模型进行分离轨迹计算,并将得到的分离轨迹参数代入Schoch判据,用于评估分离安全性,最后用所提方法对某三角翼载机外挂导弹的分离安全性进行了评估。
1 Schoch判据
1.1分离参考坐标系
为判断导弹与载机能否安全分离,需建立一个与载机结构固连的分离参考坐标系,用于描述导弹相对载机的相对运动。分离参考坐标系和弹体坐标系如图1所示。
a)分离参考坐标系O′-x′y′z′:原点O′为导弹弹体在挂架平面内的最高点;O′x′轴位于挂架平面内,指向前方为正,与载机体轴平行;x′O′z′平面平行于载机的纵向对称面;O′z′轴垂直于O′x′轴,向下为正;O′y′轴由右手定则确定。
b)弹体坐标系O-xyz:原点O为导弹质心;Ox轴与弹体纵轴重合,指向头部为正;Oz轴位于弹体纵向对称面内与Ox轴垂直,指向下为正;Oy轴垂直于xOz平面,方向由右手定则确定。
O′-x′y′z′系固定于载机上,随载机运动。在分离初始时刻,O′-x′y′z′,O-xyz两系的三轴相互平行。
1.2分离过程两个阶段
为保证导弹能顺利地在载机上分离,一般会使用分离助推器(以下简称助推器),助推器在导弹前后两端分别施加向下的作用力,如图2所示。
作用力F1,F2既可使导弹快速脱离载机,也能抵消导弹分离过程中急剧增大的低头俯仰力矩。助推器的作用时间有限,根据助推器是否工作,将整个分离过程分为两个阶段。
阶段1:导弹从载机分离,助推器工作,设其工作时间为t0,则0 阶段2:助推器工作结束,t>t0为第二阶段。 1.3安全分离判据 一般认为,在第一阶段0 若分离过程中弹体上任意一点始终处于x′O′y′平面下方,则可认为导弹不会与悬挂臂等载机结构相撞,分离过程可视为安全分离。反之,若分离过程中弹体上某点位于x′O′y′平面上方,则认为导弹与机翼发生碰撞,分离过程不安全。 导弹上任意一点在分离过程中相对参考坐标系的铅垂位移δz′为 (1) 式中:Δv,Δa分别为导弹上任意一点相对载机的相对速度和相对加速度。若导弹上任意一点在分离过程中时刻均满足δz′≥0,则分离过程安全,即 (2) 当Δv>0,Δa>0时,式(2)一定成立,由此可建立铅垂方向上由相对速度-相对加速度决定的安全区域如图3所示。其中Δa为横轴,Δv为纵轴,若分离过程中导弹的相对速度和相对加速度始终位于第一象限,则分离过程安全。 (3) 式中:rmax为导弹最大半径[2]。 Schoch判据式(3)的物理含义为:助推器在时刻t0结束工作,为保证分离的安全性,在时刻t0后0.25 s时,导弹必须下降的最小距离为导弹的最大半径。 根据Schoch判据,式(1)改写为 (4) 安全分离区域如图4所示。 图4中:标注的三个区域描述如下。 a)区域Ⅰ:相对速度和相对加速度都较大,有足够的安全裕度。 c)区域Ⅲ:尽管导弹相对速度和相对加速度均为正,但幅值较小,安全裕度较小,不满足Schoch条件,分离过程不安全。 上述三个区域之外的其他区域,分离过程均不安全。 1.4安全分离判据无量纲化 (5) 无量纲化后的安全分离区域如图5所示。 需说明的是:判据式(5)是判断机载导弹分离过程是否是安全分离的充分条件而非必要条件。在分离过程中,弹头点和弹尾点是最危险的2个点,对一些机载导弹的分离过程,如弹头点的相对速度和相对加速度(Δ2nose,Δ1nose),弹尾点的相对速度和相对加速度(Δ2tail,Δ1tail)均落在图5所示的安全分离域内,该分离过程一定安全;若两个点中至少有1个位于不安全分离域内,则需对该分离过程进行分析和判断才能确定该分离是否为安全分离。 Schoch判据式(3)中的Δv,Δa分别是导弹相对载机的相对速度和相对加速度。一般而言,分离开始时的载机速度和加速度是已知的,分离过程很短,载机的惯性很大,近似认为分离过程中载机的速度和加速度保持不变[2]。导弹的惯性小,分离过程中速度和加速度时刻在变,求解出分离过程中导弹的速度和加速度,根据相对运动法则,即可得到导弹相对载机的相对速度和相对加速度。因此,分离过程中导弹的运动参数求解是关键。 2.1气动力和气动力矩建模 若直接将CFD嵌入弹道计算过程,则弹道仿真所需计算量过大,本文根据“自由流模型+干扰模型”的气动建模方法,建立气动系数的近似表达。此气动建模的要点是:分离过程中导弹气动系数可视为自由流场中气动系数与受载机影响下的气动系数扰动量的叠加。 C=Cf(α,β)+Ci(r,Ω) (6) 式中:Cf为自由流条件下的导弹气动系数,是导弹攻角α、侧滑角β的函数;Ci为载机干扰下的导弹气动系数扰动量,是导弹与载机的相对位置r(x,y,z)和相对姿态Ω(俯仰角、偏航角)的函数[9]。一般认为,在相对位置中导弹与载机间的垂向距离z对气动干扰的影响最大[10]。 2.1.1 自由流气动模型 在式(6)中,自由流的求解相对简单,Cf可建立为关于α,β为变量的多项式回归模型,一般采用二次模型 Cf(α,β)=ξ1α2+ξ2β2+ξ3αβ+ξ4α+ ξ5β+ξ6 (7) 式中:ξi为多项式模型中第i项对应的系数;i=1,2,…,6。 α,β以一定规则生成试验样本点,根据样本点上的气动系数,用最小二乘法求得ξi;另一种常用的方法是通过插值得到不同攻角和侧滑角下的Cf(α,β)值。 2.1.2 扰动流气动模型 在式(6)中,Ci的影响因素中除导弹姿态角之外,还有导弹相对飞机的垂向距离z。取若干离散的z值(z=z1,z2,…,zh),在每个离散的z值处,俯仰角ϑ和偏航角ψ以一定规则生成试验样本点,在样本点上,用CFD计算或试验得到导弹的气动数据,这些气动数据减去无干扰条件下的导弹气动数据即为载机干扰数据Cizi(r,Ω)(i=1,2,…,h)[9]。 (8) ξj(z)=e-φz(η0+η1z+η2z2+…+ηszs) (9) 其中:e-φz项的物理含义是随着载机-导弹距离增加,载机对导弹的气动干扰越来越小;η0+η1z+η2z2+…+ηszs项可描述过程中的波动规律。 至此,可得Ci模型为 Ci(z,ϑ,ψ)=ξ1(z)ϑ2+ξ2(z)ψ2+ξ3(z)ϑψ+ ξ4(z)ϑ+ξ5(z)ψ+ξ6(z) (10) 2.2助推器推力和推力矩模型 助推器对导弹的作用如图2所示。助推器冲程长度为Ls,即当导弹下落的距离大于Ls后,助推器就不再对导弹起作用。设在下落距离z从0增加到Ls的过程中,前后助推器的推力为常数,有 (11) (12) (13) 式中:F1,F2分别为前侧推力和后侧推力;MF1F2为助推器产生的推力矩;f1,f2分别为前后助推器工作时产生的推力的大小。 2.3弹道模型 本文研究的是纵向平面内的分离,采用弹道计算模型为 式中:v,θ,ωy,x,z,ϑ,α为别为导弹的速度、弹道倾角、俯仰角速度、轴向位移、垂向位移、俯仰角和攻角;X,Z,My,Jy分别为导弹的阻力、升力、俯仰力矩和y轴的转动惯量。 本文仿真算例的载机和导弹如图6所示,导弹挂在某三角翼载机下方,位于载机的纵向对称面内[10-11]。 助推器对导弹的作用如图2所示,推力器推力和推力矩模型如式(11)所示。其中:f1=10 675 N;f2=42 700 N;l1=0.18 m;l2=0.33 m;Ls=0.1 m。 3.1分离弹道计算 根据本文的“自由流模型+干扰模型”的气动建模方法,基于文献[10-11]的数据,建立气动系数近似解析表达,在此基础上进行弹道仿真,仿真结果与文献[11]给出的风洞测试结果进行对比。 0~0.27 s内俯仰角和偏航角如图7所示,0~0.27 s内z向的位移如图8所示。图7中实线和虚线表示弹道仿真计算结果,符号“○”、“◇”表示文献[11]中提供的数据。 仿真结果表明:弹道仿真得到的弹道参数较好地拟合了CTS风洞试验中对应弹道参数的变化趋势,但俯仰角的拟合存在偏差,这些误差可归为建模方法自身的缺陷和CFD气动数据不完整。仿真结果基本验证了基于“自由流模型+干扰模型”的气动模型进行弹道仿真的可行性。 3.2分离安全性评估 载机-导弹分离过程的安全评估步骤如下: a)根据弹道仿真数据,得到载机-导弹相对距离为0.1 m(即助推器的冲程长度)时,t0=0.055 s。 b)计算得到Schoch边界Δ1=-0.549Δ2+0.455 4。 c)计算t=t0时刻铅垂平面内归一化Δ1,Δ2,对导弹而言,分离过程中最危险的点一般是弹头和弹尾,分别求得弹头和弹尾的状态为:弹头Δ1nose=1.699 9,Δ2nose=1.721 8;弹尾Δ1tail=1.699 9,Δ2tail=-0.703 7;质心Δ1xcg=1.450 3,Δ2xcg=0.587 9。 d)绘制安全分离区域图。 将弹头和弹尾的状态点绘制在安全分离域内,如图9所示。若弹头和弹尾的状态点均位于安全分离区域内,则可认为分离过程安全。 由图9可得如下结论: a)在0~0.055 s内,助推器提供的前后不对称推力使导弹受到抬头力矩作用,因此导弹在下降过程中,伴随抬头转动,导致弹尾的相对速度大于弹头的相对速度。 b)在0.055 s瞬间,由于助推器停止工作,导弹仅受气动俯仰力矩的作用,气动俯仰力矩为负,弹头有远离载机的趋势,弹尾有接近载机的趋势,因此弹头相对加速度为正,弹尾相对加速度为负。速度变化有滞后效应,故此刻弹头的相对速度仍小于弹尾的相对速度。 c)弹头和弹尾的状态点均位于安全分离域内,可认为该分离过程安全分离。 分离安全性评估是机载导弹分离研究的一项重要内容。Schoch判据简洁直观,便于工程应用,在使用Schoch判据时,需应用导弹分离轨迹上的参数信息,在一般的研究中常用CFD进行仿真,计算量大且耗时较长,若将CFD嵌入分离轨迹计算,则计算量大且效率较低。本文用“自由流模型+干扰模型”的气动建模方法,建立了分离过程中的气动系数解析表达式,并在此基础上进行了分离轨迹计算,在满足精度要求的同时,有效提高了计算效率。基于上述方法,可对导弹和载机分离过程中铅垂方向的安全性进行研究,得到侧向以及轴向分离安全判据,也可对有误差条件下的分离安全性进行蒙特卡罗仿真,评估各种误差对分离安全性的影响。 [1] SCHINDEL L H. Store separation[R]. North Atlantic Treaty Organization Advisory Group for Aerospace Research and Development, AGARD-AG-202, 1975. [2] COVERT E E. Conditions for safe separation of external stores[J]. Journal of Aircraft, 1981, 18(8): 624-630. [3] VADDI S, NGUYEN J, MENON P. Data mining and knowledge discovery from store separation trajectories[C]// AIAA Atmospheric Flight Mechanics Conference. Chicago: AIAA, 2009: 5732. [4] 郑书娥, 廖志忠. 空空导弹机弹分离安全性研究[J]. 四川兵工学报, 2015, 36(5): 17-19+23. [5] 聂璐, 向锦武. 飞机外挂物投放安全性的参数影响分析[J]. 飞行力学, 2011, 29(2): 25-28. [6] 祁洋, 范绪箕. 飞机安全性设计的外挂物投放数值方法[J]. 上海交通大学学报, 2005, 39(5): 836-839. [7] 刘刚, 肖中云, 王建涛, 等. 考虑约束的机载导弹导轨发射数值模拟[J]. 空气动力学学报, 2015, 33(2): 192-197. [8] 王晓鹏. 导弹弹射发射分离轨迹的数值研究[J]. 弹箭与制导学报, 2012, 32(3): 69-72. [9] CARTER R, LIND R. Parametric modeling for store separation aerodynamics using system identification[C]// AIAA Atmospheric Flight Mechanics Conference, 2012. Minneapolis: AIAA, 2012: 4510. [10] CHING T K. Grid survey approach to store separation trajectory prediction[J]. Journal of Aircraft, 2000, 37(4): 736-738. [11] HEIM E. CFD wing/pylon/finned-store mutual interference wind tunnel experiment[R]. Arnold Engineering Development Center, AEDC-TSR-91-P4, 1991. SafetyAssessmentforStoreSeparation WANG Hui-zhe1, LI Xiang1, WANG Xiao-peng2, GUO Yu-heng1 (1. School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China;2. Shanghai Electromechanical Engineering, Shanghai 201109, China) In order to assess the safety of the store separation quickly and efficiently, the Schoch’s criterion for determining the safety of the aircraft-missile separation was derived based upon the relative motion between the aircraft and the missile.Based on the missile dynamic model of the separation process, which was established with the hypothesis that the total aerodynamic force could be regarded as “free flow+interference flow”, the relative velocity and acceleration between the aircraft and the missile were calculated and substituted into the Schoch’s criterion to assessthe safety of the separation.Using the above method, the security evaluation of the external missile separation process of a delta wing was carried out, and the feasibility of this method was verified. missile; aircraft; store separation; relative motion; aerodynamic modeling; safe separation criteria; relative velocity; relative acceleration 1006-1630(2017)05-0124-06 2016-11-25; 2016-12-25 上海航天创新技术基金资助(SAST20150141055) 王慧哲(1993—),女,硕士生,主要研究方向为飞行器总体设计、弹道优化和机器学习等。 TJ762.2 A 10.19328/j.cnki.1006-1630.2017.05.020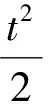
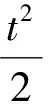

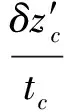
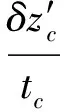
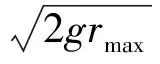
2 分离轨迹计算
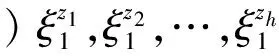
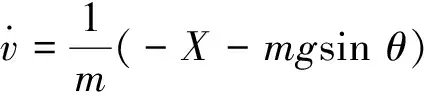
3 仿真算例
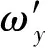
4 结束语
