修正飞针测试系统测试点坐标的解决方法

左 宁，高慧莹

(中国电子科技集团公司第四十五研究所，北京 100176)

修正飞针测试系统测试点坐标的解决方法

左 宁，高慧莹

(中国电子科技集团公司第四十五研究所，北京 100176)

飞针测试系统是用来测量混合电路板、LTCC基板、PCB板的各网络间开路、短路、绝缘以及电容的专业电子芯片检测设备。针对飞针测试系统中测试坐标点的修正提出了一种解决方法，不仅能准确得出对待测基片的平移偏距，也能够通过算法计算出待测基片的旋转角度，综合考虑平移和旋转这两点的因素最终确定待测点的实际位置坐标。

飞针测试系统；坐标修正；平移偏距；旋转角度

飞针测试系统（如图1）为双面电子芯片检测设备，该设备通过软件控制可以对混合电路板、LTCC基板、PCB板的各网络间的开路、短路、绝缘以及电容进行测试，是电子芯片制造流水线上不可或缺的重要检测设备。

在飞针测试设备的实际运行中，由于待测基片上的待测焊盘尺寸普遍很小，因此对每个测针的定位精度提出了很高的要求，同时由于夹具工艺、人工误差、烧结膨胀率等因素，从工艺文件中提取出来的测试点坐标和实际的焊盘点坐标间存在一定的偏差，这就导致了飞针设备不仅要从机械结构的角度达到很高的电机定位精度，而且更要在软件算法上将基片实际位置的平移偏距和旋转角度精确计算出，并将坐标点进行修正。修正后的待测基片测试点坐标的精确度将直接影响到整体设备的测试质量以及测试效率。

图1 双面卧式飞针测试系统

1 坐标修正软件流程及计算方法

修正待测基片坐标点的软件流程为在软件基准点对准功能中通过选取测试文件中的两个特征点Tp1和Tp2以他们在文件中的相对位置和通过CCD观察到的实际位置为依据，计算得出基片夹持后的XY向偏距以及它的旋转角度，如图2所示选取了左上角的Tp1以及右下角的Tp2。

在选好基准点后，在基准点对准功能中进行修正，如图3所示（已经对准了Tp1的实际位置）可以看到此时待测基片旋转的角度比较大。

对准好Tp1后软件对Tp2进行位置定位，如图4所示为Tp2通过文件中读取到的与Tp1的位置偏差自动得出的位置，由于旋转和平移的关系，视野内并没有看到第二个基准点Tp2，此时它的坐标已被记录。

通过移动电机观察CCD视图找到Tp2的实际位置Tp2′并将其坐标记录下来，如图5所示，此时通过Tp1、Tp2以及Tp2′的坐标即可计算出待测基板的平移距离以及旋转角度。

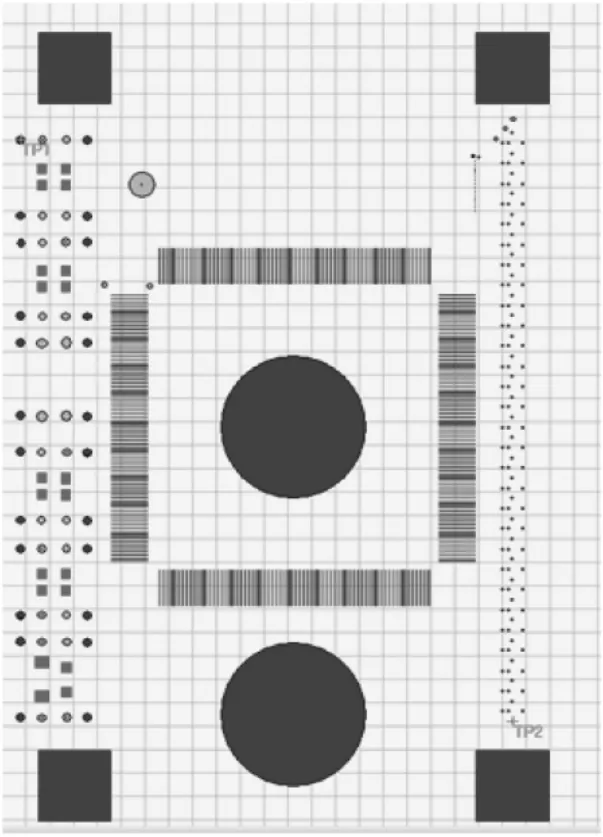
图2 在图形界面下选取基准点

图3 CCD视图下对准第一个基准点

图4 CCD视图下第二个基准点参考位置

1.1 待测基片平移偏距的计算

本文中确定待测基片的平移偏距采用以第一个基准点为准，也就是求第一个基准点的平移位置误差，方法为通过求出第一个基准点Tp1的实际位置坐标（XTp1′，YTp1′）和测试文件中记录的位置（XTp1，YTp1）之间的差值即可得出基片平移的X向以及Y向的偏距，计算公式为：

图5 确定第二个基准点的实际位置

1.2 求旋转角度θ以及确定旋转方向的方法

本文中所述方法需要求出的旋转角度通过在基准点对准时记录下第一个基准点的实际坐标（XTp1，YTp1）、从文件中读取并平移修正后的第二个基准点坐标（XTp2，YTp2）以及第二个基准点的实际位置 （XTp2′，YTp2′） 即可求得 （XTp2，YTp2） 以（XTp1，YTp1）为圆心旋转到（XTp2′，YTp2′）的位置所旋转的角度θ，如图6所示。

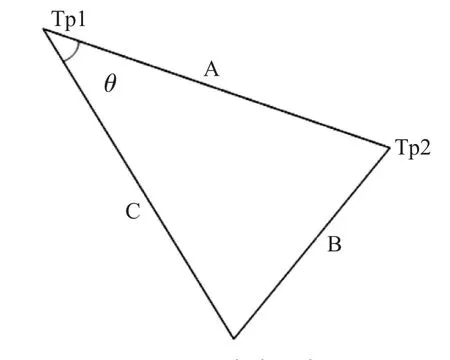
图6 旋转角度示意图

其中A、B、C分别为这个三角形的3条边，由于3点的坐标已知，即可用以下公式计算出这3条边的长度：

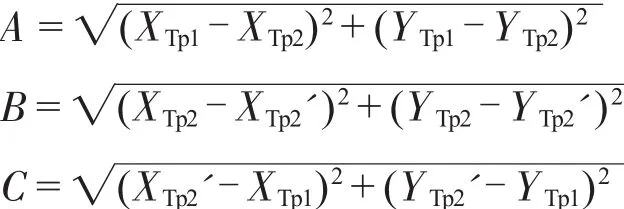
已知三角形3边长度，即可用余弦定理求出cosθ的值，并且用cosθ的值求出sin θ，所用公式为：

确定基片的旋转方向，只需要对比Tp2′与Tp2两点的Y向坐标大小即可，当YTp2′＜YTp2时认为基片为顺时针旋转，否则为逆时针旋转。

1.3 通过旋转矩阵修正坐标

在计算出待测基片的平移偏距以及旋转角度后，即可使用旋转矩阵对基片上的每个点进行修正。已知，当一个坐标系中的点绕其原点旋转角度θ后所用到的旋转矩阵为：

（1）顺指针旋转时所用旋转矩阵

（2）逆时针旋转时所用旋转矩阵

参考以上旋转矩阵，当选取圆心坐标为（XTp1，YTp1）且旋转角度为θ时，基片上每一点实际坐标（X，Y）与从测试文件中提取后经过平移修正的坐标（X0+XOffset，Y0+YOffset）之间映射关系修正矩阵分别为：

（1）待测基板顺指针旋转时：

（2）待测基板逆指针旋转时：

得出以上矩阵的方法为先将待测基片上需要修正坐标的点平移(-XTp1，-YTp1)将问题转化为以待测基片坐标原点为圆心旋转的问题，得出旋转后的坐标再反向平移（XTp1，YTp1），即得到实际基片上的坐标位置。

将此矩阵展开后即可得到实际需要用到的坐标修正公式：

（1）待测基板顺指针旋转时：

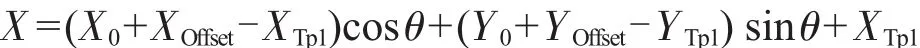
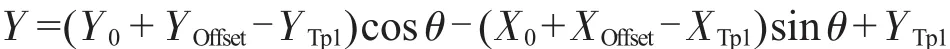
（2）待测基板逆指针旋转时：

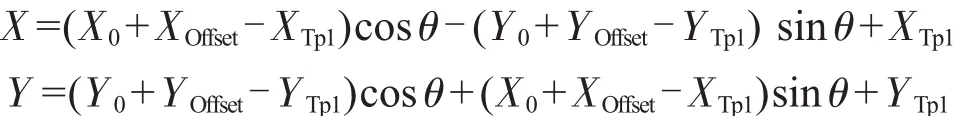
2 最终得出的坐标修正方法

在设备实际测试中对坐标的修正还要考虑到待测基片的膨胀率以及CCD与针之间的偏距（XCCDOffset和YCCDOffset）并且也要将顺时针旋转和逆时针旋转两种情况分别进行处理，结合之前的旋转矩阵代入这些参数后将其展开即得到最终程序中用到的坐标修正公式：

（1）待测基板顺指针旋转时：

（2）待测基板逆指针旋转时：

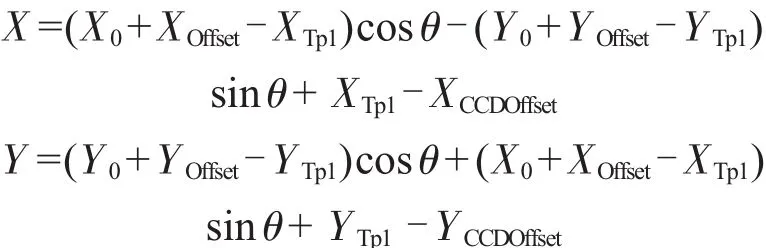
3 算法所涉及的代码

以下是本文中所涉及到的计算方法写入到实际程序应用中的代码，部分做了注释，以供参考：

4 结束语

此次重新改进后的坐标修正算法解决了之前老算法只能修正平移不能修正旋转角度的问题，具有较强的实际应用价值，其程序算法流程如图7所示。

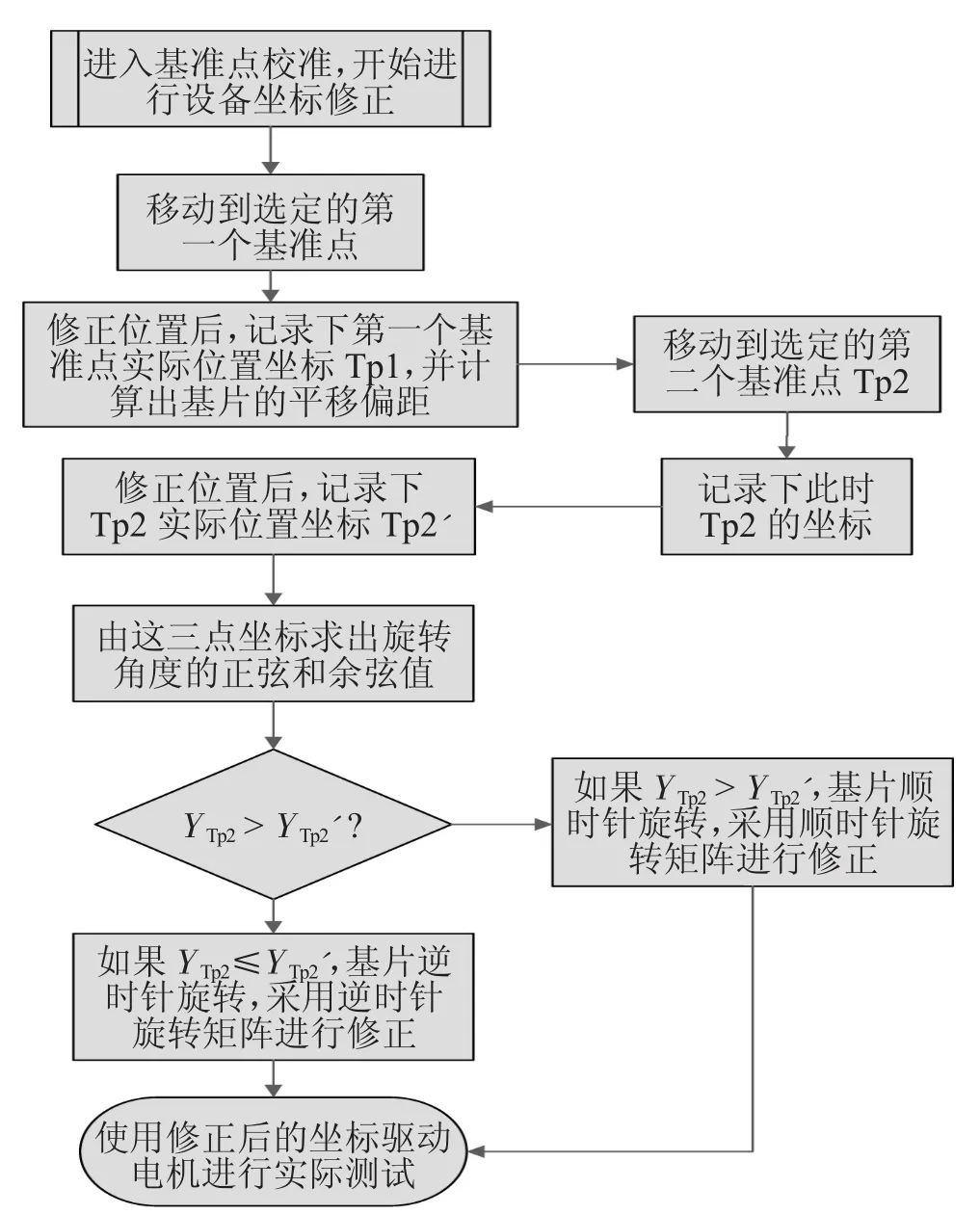
图7 角度修正算法流程图

经过多次试验证明此方法可行，修正后的坐标精度能够达到±10 μm左右。在实际设备工作中，减少了因为基片放置位置的人工误差导致的测试失准，提高了设备整体的可靠性和运行效率。此方法目前仍处于试验阶段，在进一步的改进中，力争达到更高的修正精度。

[1] 方文波.线性代数及其应用[M].北京：高等教育出版社，2011.

[2] 杨晓鹏.Visual C++6.0实用编程技术[M].北京：中国水利水电出版社，1999.

[3] 吕磊，刘国敬，左宁.DWG格式的飞针测试文件转换[J].电子工业专用设备，2014.43(6)：37-42.

Correction Method of Test Point Coordinate for Flying Probe Tester

ZUO Ning，GAO Huiying
(The 45thResearch Institute of CECT，Beijing 100176，China)

Flying probe test system is used to measure the network hybrid circuit board，LTCC board，PCB board of the open circuit and insulation and capacitance of professional electronic chip testing equipment This paper presents a method to solve the coordinate point correction test flying probe test system，not only can get accurate measurement of substrate offset translation treatment，can also be calculated by the algorithm to measure the rotation angle of the substrate，considering the translation and rotation of these two eventually determine the actual position coordinates of the measured point the.

Flying probe test system；Coordinate correction；Offset translation；Rotation angle

TN407

B

1004-4507(2017)05-0036-06

2017-07-27

左宁（1985-），男，甘肃省兰州市人，工程师，毕业于兰州交通大学计算机科学与技术专业，硕士，目前研究方向为半导体专用设备的工控软件研发，担任探针、飞针等电子元器件测试设备的软件组负责人。