基于二次Bezier曲线的无线传感网避障路径规划研究*
2017-11-03张美燕蔡文郁周莉萍
张美燕,蔡文郁,周莉萍
(1.浙江水利水电学院 电气工程系,杭州 310018;2.杭州电子科技大学电子信息学院,杭州 310018)
项目来源:浙江省自然科学基金项目(LY18F030006,LY15F030018,Y18F030025);国家自然科学基金项目(6170060208)
2017-03-27修改日期2017-06-09
基于二次Bezier曲线的无线传感网避障路径规划研究*
张美燕1,蔡文郁2*,周莉萍1
(1.浙江水利水电学院 电气工程系,杭州 310018;2.杭州电子科技大学电子信息学院,杭州 310018)
用固定Sink节点进行无线传感网内数据采集的传统方式会导致热点区域(hot spot)问题,而采用移动Sink节点进行数据采集可以克服这个问题,从而达到均衡网络能量分布与延长网络生命周期的效果。本文针对类车型机器人作为无线传感网中移动数据汇聚节点的应用场景,提出了一种基于Bezier连续曲线的移动Sink节点避障路径规划算法。本文构建了连续分段Bezier曲线为巡航轨迹,采用人工势场中的斥力场理论实现对多个障碍物的智能躲避,动态调节二次Bezier曲线的内部控制点位置,将障碍物排斥在二次Bezier曲线之外。仿真结果验证本文提出的算法可以实现移动Sink节点规划路径的避障功能,同时Bezier曲线规划算法简单,计算量较小。
无线传感器网络;Bezier曲线;路径规划;障碍避免
通过合理规划移动Sink节点的运动路径以实现无线传感器网络中多传感器节点的数据收集是目前的一大研究热点[1-2]。无线传感器网络的避障路径规划问题是指:在具有多个凸形障碍物的无线传感器网络配置空间(Configuration Space)中,按照设定的路径优化目标,寻找一条能够遍历所有传感器节点的无碰撞路径[3]。传统的避障路径规划中往往不考虑路径的曲率连续性,只考虑了最小时间、最短巡航距离或最少能量消耗等原则,从而找到一条最优解或次优解,因此获得的路径是一连串由直线段构成的避障路线。由于非连续运动曲线对于车型机器人的运动方向造成突变,不利于机器人保持平稳的运动速度和能量消耗。为了使车辆型机器人行驶路线平滑,不存在拐点,整体轨迹应由分段连续曲线构成[4]。为满足以上的几个特征,Bezier曲线[5]利用了曲线的切矢量性,即Bezier曲线的起点和终点处的切线方向和控制点多边形的第1条边及最后一条边的走向一致,这对于类车型机器人,通过Bezier曲线模型构造的运动轨迹,非常符合类车型机器人的动力学特征。
目前已有一些研究采用了Bezier和B-Spline等样条曲线对避障路径规划问题和连续性路径规划问题进行了研究。文献[6]提出了一种基于多段线方式的避障曲线,然后利用三次样条曲线简化实现;文献[7-8]提出了一种基于有理三次样条曲线的避障路径规划技术;文献[9]提出了一种利用Bezier曲线描述路径与改进粒子群优化算法相结合的路径规划方法;文献[10]提出了一种既能使曲线规避所有障碍物,又能使曲线在整体上保持G2连续的低次避障代数样条曲线;文献[11]提出通过遗传算法再结合B样条曲线规划出平滑的避障路径的方法。除此之外,文献[12-14]研究了存在多个移动机器人情况下如何实现路径规划与协作避障的方法。上述研究成果都对机器人移动路径规划问题的某些方面做了深入研究,但是有些文献提出的曲线构造算法过于复杂,需要求解高次方程,有些研究采用了遗传算法等启发式优化算法,计算复杂度过高。
除此之外,在实际的无线传感器网络中,移动Sink节点进行数据收集往往需要一段时间,因此一般会在采集传感器节点附近停留,完成数据采集后再按路径向下一个传感器节点行驶。但是行驶过程中运动方向突变对减速齿轮的伤害和会减速打滑而带来的位置误差,因此只需要在分段曲线内满足较高连续性即可,这样可以极大地降低路径计算复杂度。
本文结合了分段连续二次Bezier曲线和人工势场算法,实现了一种基于连续二次Bezier曲线的避障路径规划方法,从而避免由于障碍物存在导致移动失效的情况,为无线传感器网络中移动Sink节点的高效数据采集提供了保证。
1 问题描述
假设无线传感器网络区域内随机分布了S个传感器节点Ni(i=1,2,…,S),其坐标为(xi,yi)(i=1,2,…,S)和Q个凸形障碍物Oj(j=1,2,…,Q),其坐标为(xj,yj)(j=1,2,…,Q),1个移动Sink机器人沿着预定的轨迹移动,按序采集每个传感器节点的传感数据,如图1所示。本文研究的优化问题如下:假设移动Sink节点沿着预定的路径对各个传感器节点进行数据采集,且该路径具有避开障碍物的功能。优化目标为寻找一条巡航总距离最短的避障闭合曲线来遍历所有的传感器节点,该曲线满足曲率连续的约束条件。数学模型如下所示:
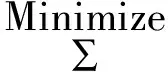
(1)
(2)

(3)
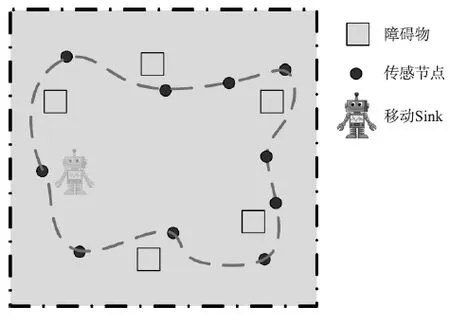
图1 避障路径规划示意图
Bezier曲线的形状由通过一组多边折线(控制点多边形)的各顶点定义,只有第1个顶点和最后一个顶点在曲线上,其余的顶点用于定义曲线的导数、阶次和形状,第1条边和最后一条边则表示了曲线在两端点处的切线方向。其数学表达式由多项式混合函数推导,如下所示:
(4)
式中:Pi为曲线各个控制点的位置向量,顺序连接从P0到Pn的折线被称为Bezier曲线的控制多边形,Bn,i(u)为伯恩斯坦基多项式,定义如下:

(5)
由于三次Bezier曲线计算量比二次Bezier更多更复杂,因此本文将只采用二次Bezier曲线作为相邻传感器节点之间巡航的路径曲线。由于式(1)~(3)所提出的最优化模型需要多阶曲线来规划,计算复杂度较大,本文采用的Bezier曲线规划较为简单,属于一种次优解。
由于Bezier曲线的长度计算公式如式(6)所示,无法直接进行积分运算,只能粗略获取Bezier曲线长度的限值。文献[15]提出了计算曲线长度的近似式(7),为了简单起见,本文也以此作为Bezier曲线长度计算的公式,所以对于二次Bezier曲线而言,Bezier距离计算可以等价于首位控制点的欧式距离。

(6)

(7)
2 基于二次Bezier曲线的避障路径规划算法
对于一般类车型机器人,满足C2连续的移动路径已经足够满足巡航速度和动力性需求,关于Bezier曲线的连续性如下定义:
定义1C(u)满足C2连续的充要条件,C″(u1)=C″(u2) (u1≠u2),即要求曲线二阶导数连续。
Bezier曲线的导数定义为:
(8)

定义2f1和f2满足G0连续的充要条件:f1(1)=f2(0)。即f1的终点与f2的起点重合,但是曲线在连接点处不能保证是光滑连接。

根据Bezier曲线的基本性质,可以推导出以下定理,这些定理可以用于本文的避障路径规划算法:
定理1当且仅当障碍物在控制点多边形内部时,才需要调节内部控制点的位置实现避障。
证明由Bezier曲线的凸包性可知,Bezier曲线全段位于由控制点构成的闭合凸包内,因此,如果当障碍物在控制点多边形外部时,Bezier曲线不会与障碍物发生碰撞。当且仅当障碍物在控制点多边形内部时,才需要调节Bezier曲线形态,实现避障。
定理2障碍物是否处于控制点多边形内部的判断条件必须满足:
证明控制点三角形ΔP0P1P2内部的任意一点P(α,β)都可以表示如下:
选取慢性心力衰竭合并2型糖尿病患者74例作为研究对象,将其随机分为替米沙坦组和雷米普利组,各37例,比较两组慢性心力衰竭治疗效果、空腹血糖水平、胰岛素水平及不良反应发生率。入院时,患者均符合美国心脏病协会制定的关于慢性心力衰竭的诊断标准,1999年WHO制定的关于2型糖尿病的诊断标准,空腹血清C肽平均指数为(2.61±0.21)nmol/L,排除免疫系统疾病者、血液系统疾病者、精神疾病者等,其中,替米沙坦组女12例,男25例,平均年龄(36.92±2.14)岁;雷米普利组女11例,男26例,平均年龄(37.16±2.09)岁。两组患者一般资料比较,差异无统计学意义(P>0.05)。
P(α,β)=P1+α(P0-P1)+β(P2-P1)
(α+β<1,α>0,β>0)
(9)
当α+β=1时,P(α,β)在P0P2线段上;当α=0时,P(α,β)在P1P2线段上;β=0,P(α,β)在P0P1线段上。由上式可得如下方程组,通过求解方程组可得α和β的值,通过α和β的条件判断,从而得知障碍物是否在控制点三角形ΔP0P1P2内部。
(10)

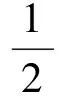
(11)
C′(1/2)=P2-P0
(12)

图2 二次Bezier避障曲线示意

基于人工势场的方法是机器人运动规划中一种常用方法,通过对障碍物建立排斥势场,对目标点建立引力势场,综合目标对机器人的吸引力以及障碍物对机器人的排斥力,使机器人绕开障碍物向目标点移动而形成运动规划。但是人工势场法也有其内在的局限性,而且也有较为复杂的计算量。本文利用人工势场方法中的斥力势场理论对Bezier避障曲线的内部控制点进行调整,但是本文的避障算法只引入了人工势场中的斥力场来分析障碍物排斥范围,即规划曲线路径要避开障碍物的斥力场区域,其计算公式如下:
(13)
式中:ρi表示物体和障碍物之间的距离,η表示斥力尺度因子,ρ0表示每个障碍物的斥力场半径。根据上述定义,本文假设只要Sink节点巡航路径不通过障碍物的斥力场区域,那么就是安全的;如果Sink节点巡航路径通过了障碍物的斥力场区域,那么就认为与障碍物发生了碰撞。障碍物斥力场强度与斥力尺度因子之间的关系如图3所示。

图3 障碍物斥力场强度曲线
定理4二次Bezier曲线f1和f2满足G1连续的条件是前后两条Bezier曲线的两个内部控制点与两条曲线交点成同一直线,并以两条曲线交点为中点。

图4 G1分段连续二次Bezier曲线示意



图5 仿真场景示意图
3 仿真结果
本文采用MATLAB R2010a仿真平台对所提出的算法进行验证。仿真环境的主要参数为:区域半径为100×100×100的立方体型三维空间内随机分布分布着S个传感器节点和Q个凸形障碍物,斥力尺度因子η=10,障碍物的斥力场半径ρ0=1,算法参数ν=1/η=0.1,仿真场景示意如图5所示,其中图5(a)为传感器节点和障碍物的空间分布,图5(b)为障碍物的斥力场分布。仿真采用的AUV能量模型简化为距离模型,AUV消耗能量与其所巡航的距离成正比。在本文仿真中,传感器节点的数量从5、10、20变化,即S=5/10/20,凸形障碍物数量从5、10变化,即Q=5/10。如图6所示,如果采用最小距离旅行商问题的直线方法进行Sink节点的路径规划,该曲线与5个障碍物中的2个障碍点发生了碰撞。因此,虽然采用该方法可以获得最小的总巡航距离,但是最短直线路径肯定无法避免全部的障碍物。

图6 无避障功能最短路径规划图
本文采用的二次Bezier曲线避障,只有一个内部控制点需要调节,控制量较少,算法简单。如果采用现有研究中的更高阶数样条曲线作为规划路径,实施避障路径规划可能达到更优的路径长度,但是要满足路径的C2连续,需要调整更多的参数,不适合于计算能力较低的移动Sink节点。因此本文仿真过程只比较了不同数量障碍物和待访问传感器节点下的避障性能。
由式(7)可知,本文假设Bezier曲线长度可简单等价于首位控制点的欧式距离。因此本文提出的基于二次Bezier曲线的避障碍路径规划算法中,可以借鉴图6无避障功能最短路径规划图所用的最小总距离旅行商问题的求解方法。首先根据最小总距离旅行商问题求解出移动Sink巡航的传感器节点次序,以此获取最小距离路径规划的求解。然后利用本文提出的Bezier避障曲线算法,对两两传感器节点之间的满足C2连续路径进行计算,最终得到整个无线传感网移动数据收集总路径曲线。
在5个传感器节点和5个障碍物,10个传感器节点和5个障碍物,20个传感器节点和10个障碍物情况下,有无避障功能的曲线对比分别如图7、图8和图9所示。图中粉红色方块为障碍物,红色圆圈为传感器节点,绿色折线表示控制点多边形,蓝色曲线表示规划路径。从图7可以发现,只有右下方两个障碍物存在于控制点三角形内,所以Bezier曲线的内部控制点进行了下移,并且缩短了曲线距离,其余部分曲线与无故障避免曲线相同。从图8可以发现,本文提出的障碍避免规划路径已经避开了所有障碍物。从图9可以发现,当障碍物数量较多时,Bezier曲线避障规划路径也能避开障碍物。因此,通过多次仿真曲线可知,应用本文提出的基于二次Bezier曲线的避障路径规划算法,可以实现多个障碍物的有效避免。

图9 Bezier曲线避障路径(S=20,Q=10)

图7 Bezier曲线避障路径(S=5,Q=5)
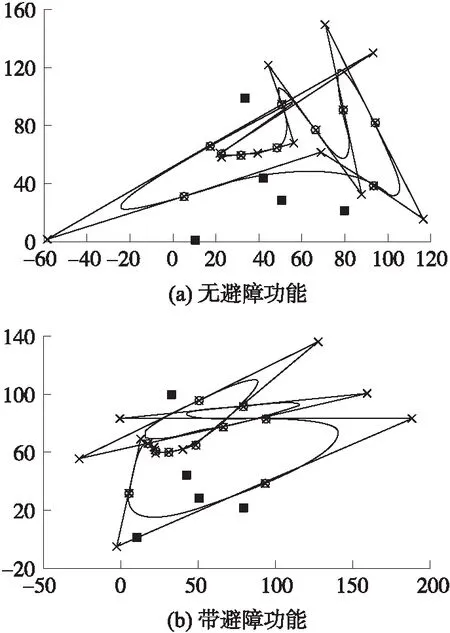
图8 Bezier曲线避障路径(S=10,Q=5)
4 结语
本文综合考虑了满足C2连续二次Bezier曲线和人工势场法中斥力场的分析方法,提出了一种满足分段连续的二次Bezier避障曲线,保证无线传感器网络中的Sink节点对多个凸形障碍的有效避障。仿真结果验证了本文提出的基于二次Bezier曲线的无线传感网避障路径规划算法以较低的计算复杂度来实现高效率避障。后续工作将考虑无线传感器网络中存在有多个Sink节点时如何优化规划路径,使得多个Sink节点协同完成数据采集任务,同时避开障碍物以及避免自我碰撞。
[1] 张美燕,蔡文郁,周丽萍. 三维水下移动传感网多目标有向路径覆盖增强研究[J]. 传感技术学报,2014,27(1):100-106.
[2] 蒋富龙,刘昊. 面向批量数据采集的无线传感器网络双路径采集协议[J]. 传感技术学报,2013,9(9):1270-1275.
[3] Latombe J C. Robot Motion Planning. Norwood[M]. Kluwer M A. Academic Publishers,1991.
[4] 胡诚,汪芸,王辉. 无线可充电传感器网络中充电规划研究进展[J]. 软件学报,2016,27(1):72-95.
[5] 王家润,赵南松,华文元,等. 分段连续三次Bezier曲线控制点的构造算法[J]. 计算机工程与应用,2010,46(22):190-193.
[6] Li Z,Meek D S,Walton D J. A Smooth,Obstacle-Avoiding Curve[J]. Computers and Graphics,2006,30(4):581-587.
[7] Meek D S,Ong B H,Walton D J. A Constrained GuidedG1Continuous Spline Curve[J]. Computer-Aided Design,2003,35(6):591-599.
[8] Meek D S,Ong B H,Walton D J. Constrained Interpolation With Rational Cubics[J]. Computer Aided Geometric Design,2003,20(5):253-275.
[9] 朱东伟,毛晓波,陈铁军. 基于改进粒子群三次Bezier曲线优化的路径规划[J]. 计算机应用研究,2012,29(5):1710-1712.
[10] 陈军. 连续的低次避障代数样条曲线[J]. 中国图象图形学报,2013,18(6):718-723.
[11] 王宪,盛巍,宋书林,等. 基于遗传算法和B样条曲线的平滑避障路径规划[J]. 计算机系统应用,2012,21(2):65-71.
[12] Florin S,Vlad-Mihai I,Ionela P. Obstacle Avoidance Via B-Spline Parameterizations of Flat Trajectories[C]//Proceedings of the 24th Mediterranean Conference on Control and Automation,June 21-24,2016,Athens,Greece.
[13] Igor S,Gregor K. Cooperative Collision Avoidance Between Multiple Robots Based on Bezier Curve[C]//Proceedings of the ITI 2007 29th Int. Conf. on Information Technology Interfaces,Cavtat,Croatia,June 25-28,2007:451-456.
[14] 杨冬梅. 基于无线传感器网络的多移动机器人避障方法研究[D]. 哈尔滨:哈尔滨工业大学,2013.
[15] Press W H,Teukolsky S A,Vetterling W T,et al. Numerical Recipes in C++[M]. 2nd ed. Cambridge,England:Cambridge University Press,2002.
ObstaclesAvoidanceBasedQuadraticBezierCurvePathPlanningforWirelessSensorNetworks*
ZHANGMeiyan1,CAIWenyu2*,ZHOULiping1
(1.School of Electrical Engineering,Zhejiang University of Water Resources and Electric Power,Hangzhou 310018,China; 2.School of Electronics and Information,Hangzhou Dianzi University,Hangzhou 310018,China)
The traditional sensory data collection method with fixed Sink node will lead to hot spot problem. To overcome this problem,mobile data collection by mobile Sink is proposed so as to balance network energy distribution and prolong network lifecycle. Aiming at the application scenario of the vehicle-like robot as a mobile data aggregation node in wireless sensor networks,this paper proposes a continuous quadratic Bezier curves based obstacle avoidance path planning algorithm for mobile Sink node. Firstly,some segmented continuous Bezier curves are constructed as a whole cruise trajectory. Secondly,the repulsive effect of multiple obstacles is analyzed by artificial potential field method. As a result,the position of internal control points of Bezier curve is dynamically adjusted with repulsive potential field,and adjacent obstacles can be excluded from delta-shaped region by quadratic Bezier curve. Simulation results verify that the proposed method can realize multiple obstacles avoidance in the planning path of mobile Sink node with smaller computational complexity.
wireless sensor networks;bezier curve;path planning;obstacles avoidance
TP393
A
1004-1699(2017)10-1596-06
10.3969/j.issn.1004-1699.2017.10.024

张美燕(1983-),女,副教授,从事无线传感网络、新型能源技术、物联网技术等研究,主持和参与浙江省自然科学基金2项,浙江省公益性行业专项3项,浙江省水利厅科技项目2项,参与浙江省厅级项目多项。近年来发表论文20余篇,被三大索引收录论文10余篇,申请发明专利和实用新型专利30余项;

蔡文郁(1979-),男,博士,副教授,主要从事物联网、无线传感网及嵌入式技术研究。主持和参与国家自然科学基金2项、浙江省自然科学基金3项、浙江省公益性行业专项3项,国家863计划项目2项、国家海洋局行业专项1项、浙江省重大科技专项1项,横向课题10余项。近年来发表论文40余篇,被SCI/EI收录20余篇,申请专利及软著40余项,授权30余项,dreampp2000@163.com。
