2组分混合样本系统效能分析的实验性研究
2017-11-03周密汪军
周 密 汪 军
(1 芜湖市公安局刑警支队 安徽 芜湖 241000;2 安徽工程大学计算机与信息学院 安徽 芜湖 241000)
2组分混合样本系统效能分析的实验性研究
周 密1,2汪 军2
(1 芜湖市公安局刑警支队 安徽 芜湖 241000;2 安徽工程大学计算机与信息学院 安徽 芜湖 241000)
对2组分混合样本的系统效能进行公式推导,并以随机模拟法验证公式。建立2组分混合样本3个分类的系统效能定义,在此基础上自行推导数学公式,并在Identifiler系统的15个基因座上计算系统效能的公式值。应用随机模拟法设计实验,在15个基因座上计算系统效能的模拟值。以模拟值对比公式值的方式,对公式进行实验验证。结果表明,3类系统效能公式均符合模拟实验验证。Identifiler系统中,犯罪嫌疑人和受害人混合类型的系统效能(CDPC2-11)为1-1.82910×10-13,犯罪嫌疑人和未知个体混合类型的系统效能(CDPC2-1)为1-1.98396×10-8,2个犯罪嫌疑人混合类型的系统效能(CDPC2-2)为1-5.15033×10-22。3个类型的公式可应用于2组分混合样本的系统效能计算。
混合样本 系统效能 随机模拟法
1 引言
法医DNA检验中,最常见的混合样本由2个组分形成,如性犯罪案中犯罪嫌疑人和受害人的混合样品。根据组分类型,2组分混合样本分为3种类型:①犯罪嫌疑人和受害人混合;②犯罪嫌疑人和未知个体混合;③2个犯罪嫌疑人混合。这3种类型的确信概率(LR值)计算虽有报道[1],但相应的系统效能分析仍未见报道。因此,本实验首先提出2组分混合样本3种类型的系统效能定义,然后进行数学推导和模拟实验验证。
2 方法
2.1 模拟样本
按随机模拟法,自主研发软件[2]模拟Identifiler系统的15个常染色体STR基因座的随机个体和随机2组分混合样本。
2.1.1 随机个体
在单个基因座上,随机产生2个等位基因,组成随机个体的单基因座分型。等位基因的产生概率参考中国汉族人群基因频率[3]。同理在15个基因座上分别模拟,获得随机个体的Identifiler试剂盒的完整STR分型。
2.1.2 随机2组分混合样本
独立产生2个随机个体的Identifiler试剂盒STR分型,按照混合样本的形成规律,将两者混合而成2组分混合样本的Identifiler试剂盒STR分型。其中2个随机个体即为该混合样本的2个组分。将上述过程重复n次,模拟出n个2组分混合样本及其组分。
2.2 概念和公式推导
2.2.1 基本概念
本实验的2组分混合样本为理想状态:STR图谱显示混合样本全部等位基因,均为真峰,忽略伪峰;2个组分互相独立,无亲缘关系。
2组分混合样本判断标准:
(1)犯罪嫌疑人和未知个体混合类型
该类型只有犯罪嫌疑人1个已知组分,其判断标准为:①犯罪嫌疑人的等位基因均与混合样本等位基因共享,犯罪嫌疑人不含混合样本中没有的等位基因;②排除重复的等位基因后,混合样本等位基因数-犯罪嫌疑人等位基因数≤2。
(2)犯罪嫌疑人和受害人混合类型或2个犯罪嫌疑人混合类型
该2种类型中的已知组分有2个,分别称为1~2号。其判断标准为:①2个组分的等位基因均与混合样本等位基因共享,2个组分均不含混合样本中没有的等位基因;②排除重复的等位基因后,混合样本等位基因数=1号等位基因数+2号等位基因数。
根据2组分混合样本分类,基于以上混合样本判断标准,单基因座系统效能同样分为3类:
(1)犯罪嫌疑人和受害人混合类型
①混合样本匹配概率(QC2-11):单基因座上3个随机个体(称为1~3号),将1号和2号混合形成随机混合样本,将3号视为犯罪嫌疑人,1号视为受害人,则3号、1号和混合样本符合2组分混合样本判断标准的概率。
②混合样本识别能力(DPC2-11):单基因座上3个随机个体(称为1~3号),将1号和2号混合形成随机混合样本,将3号视为犯罪嫌疑人,1号视为受害人,则1号、2号和混合样本不符合2组分混合样本判断标准的概率。
(2)犯罪嫌疑人和未知个体混合类型
①混合样本匹配概率(QC2-1):单基因座上3个随机个体(称为1~3号),将1号和2号混合形成随机混合样本,将3号视为犯罪嫌疑人,则3号和混合样本符合2组分混合样本判断标准的概率。
②混合样本识别能力(DPC2-1):单基因座上3个随机个体(称为1~3号),将1号和2号混合形成随机混合样本,将3号视为犯罪嫌疑人,则3号和混合样本不符合2组分混合样本判断标准的概率。
(3)2个犯罪嫌疑人混合类型
①混合样本匹配概率(QC2-2):单基因座上4个随机个体(称为1~4号),将1~2号混合作为混合样本,将3~4号视为2个犯罪嫌疑人,则3号、4号和混合样本符合混合样本判断标准的概率。
②混合样本识别能力(DPC2-2):单基因座上4个随机个体(称为1~4号),将1~2号混合作为混合样本,将3~4号视为2个犯罪嫌疑人,则3号、4号和混合样本不符合混合样本判断标准的概率。
∵DP事件和Q事件是相互对立的事件
∴DPC2-11+QC2-11=1,DPC2-1+QC2-1=1,DPC2-2+QC2-2=1
DP的数学推导与个体识别DP类似,均为先推导Q公式,而非直接DP公式。
2.2.2 DPC2-11公式
设某基因座上A、B、C、D的基因频率分别为a、b、c、d。设定义中的1~3号随机个体的基因型概率分别为1~3号概率。假设合并概率=1号概率×2号概率×3号概率。根据2组分混合样本的基因型分为4种情况:
(1)混合样本A
∵1~3号的基因型均为A
∴合并概率1=a2×a2×a2=a6
(2)混合样本AB
∵1~3号的基因型组分为3大类:
①1号基因型为A、2~3号基因型为B/AB时,概率=a2(b2+2ab)2
②1号基因型为B、2~3号基因型为A/AB时,概率=b2(a2+2ab)2
③1号基因型为AB、2~3号基因型为A/B/AB时,概率=2ab(a2+b2+2ab)2
∴合并概率2=a2(b2+2ab)2+b2(a2+2ab)2+2ab(a2+b2+2ab)2
(3)混合样本ABC
∵1~3号的基因型组分为6大类:
①1号基因型为A、2~3号基因型为BC时,概率=a2(2bc)2
②1号基因型为B、2~3号基因型为AC时,概率=b2(2ac)2
③1号基因型为C、2~3号基因型为AB时,概率=c2(2ab)2
④1号基因型为AB、2~3号基因型为C/AC/BC时,概率=2ab(c2+2ac+2bc)2
⑤1号基因型为AC、2~3号基因型为B/AB/BC时,概率=2ac(b2+2ab+2bc)2
⑥1号基因型为BC、2~3号基因型为A/AB/AC时,概率=2bc(a2+2ab+2ac)2
∴合并概率3=12a2b2c2+2ab(c2+2ac+2bc)2+2ac(b2+2ab+2bc)2+2bc(a2+2ab+2ac)2
(4)混合样本ABCD
∵1~3号的基因型组分为6大类:
①1号基因型为AB、2~3号基因型为CD时,概率=2ab(2cd)2
②1号基因型为AC、2~3号基因型为BD时,概率=2ac(2bd)2
③1号基因型为AD、2~3号基因型为BC时,概率=2ad(2bd)2
④1号基因型为BC、2~3号基因型为AD时,概率=2bc(2ad)2
⑤1号基因型为BD、2~3号基因型为AC时,概率=2bd(2ac)2
⑥1号基因型为CD、2~3号基因型为AB时,概率=2cd(2ab)2
∴合并概率4=2ab(2cd)2+2ac(2bd)2+2ad(2bd)2+2bc(2ad)2+2bd(2ac)2+2cd(2ab)2
综上,DPC2-11=1-Q2C-11=1-(合并概率1+合并概率2+合并概率3+合并概率4)。设n为某基因座的等位基因数,Pi, Pj, Pk, Pw为该基因座第i, j, k, w个等位基因频率。将合并概率转化为全基因座形式,则DPC2-11公式为:
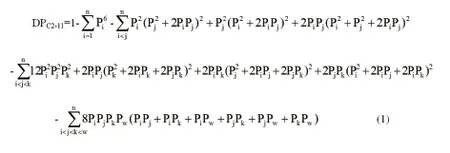
2.2.3 DPC2-1公式
设某基因座上A、B、C、D的基因频率分别为a、b、c、d。设定义中的1~3号随机个体的基因型概率分别为1~3号概率。假设合并概率=1号概率×2号概率×3号概率。分为4种情况:
(1)混合样本A
∵1~3号均为A
∴合并概率1=a2×a2×a2=a6
(2)混合样本AB
∵1~2号的基因型组合为A+B、B+A、AB+AB、A+AB、AB+A、B+AB、AB+B共计7种。
∴1号概率×2号概率的总和=a2·b2+b2·a2+2ab·2ab+a2·2ab+2ab·a2+b2·2ab+2ab·b2=6a2b2+4a3b+4ab3
∵3号基因型为A/B/AB
∴3号概率=a2+b2+2ab
∴合并概率2=(6a2b2+4a3b+4ab3)(a2+b2+2ab)
(3)混合样本ABC
∵1~2号的基因型组合为AB+BC、BC+AB、AC+BC、BC+AC、AB+AC、AC+AB、A+BC、BC+A、B+AC、AC+B、AB+C、C+AB共计12种。
∴1号概率×2号概率的总和=2(2ab·2bc+2ac·2bc+2ab·2ac+a2·2bc+b2·2ac+c2·2ab)=12(a2bc+ab2c+abc2)
∵3号可能为A/B/C/AB/AC/BC
∴3号概率=a2+b2+c2+2ab+2ac+2bc
∴合并概率3=12(a2bc+ab2c+abc2)(a2+b2+c2+2ab+2ac+2bc)
(4)混合样本ABCD
∵1~2号的基因型组合共计6种,但每种的概率均为4abcd
∴1号概率×2号概率的总和=24abcd
∵3号基因型为AB/AC/AD/BC/BD/CD
∴3号概率=2ab+2ac+2ad+2bc+2bd+2cd
∴合并概率4=48abcd(ab+ac+ad+bc+bd+cd)
综上,DPC2-1=1-Q2C-1=1-(合并概率1+合并概率2+合并概率3+合并概率4)。设n为某基因座的等位基因数,Pi, Pj, Pk, Pw为该基因座第i, j, k, w个等位基因频率。将合并概率转化为全基因座形式,则DPC2-1公式为:
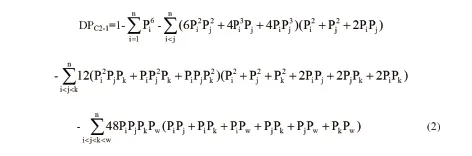
2.2.4 DPC2-2公式
设某基因座上A、B、C、D的基因频率分别为a、b、c、d。设定义中的1~4号随机个体的基因型概率分别为1~4号概率。假设合并概率=1号概率×2号概率×3号概率×4号概率。分为4种情况:
(1)混合样本A
∵1~4号均为A
∴合并概率1=a2×a2×a2×a2=a8
(2)混合样本AB
∵1~2号的基因型组合为A+B、B+A、AB+AB、A+AB、AB+A、B+AB、AB+B共计7种。
∴1号概率×2号概率的总和=a2·b2+b2·a2+2ab·2ab+a2·2ab+2ab·a2+b2·2ab+2ab·b2=6a2b2+4a3b+4ab3
∵3号概率×4号概率的总和=1号概率×2号概率的总和
∴合并概率2=(6a2b2+4a3b+4ab3)2
(3)混合样本ABC
∵1~2号的基因型组合为AB+BC、BC+AB、AC+BC、BC+AC、AB+AC、AC+AB、A+BC、BC+A、B+AC、AC+B、AB+C、C+AB共计12种。
∴1号概率×2号概率的总和=2(2ab·2bc+2ac·2bc+2ab·2ac+a2·2bc+b2·2ac+c2·2ab)=12(a2bc+ab2c+abc2)
∵3号概率×4号概率的总和=1号概率×2号概率的总和
∴合并概率3=[12(a2bc+ab2c+abc2)]2
(4)混合样本ABCD
∵1~2号的基因型组合共计6种,但每种的概率均为4abcd
∴1号概率×2号概率的总和=24abcd
∵3号概率×4号概率的总和=1号概率×2号概率的总和
∴合并概率4=(24abcd)2
综上,DPC2-2=1-Q2C-2=1-(合并概率1+合并概率2+合并概率3+合并概率4)。设n为某基因座的等位基因数,Pi, Pj, Pk, Pw为该基因座第i, j, k, w个等位基因频率。将合并概率转化为全基因座形式,则DPC2-2公式为:
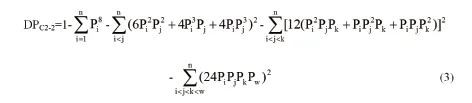
2.3 模拟实验验证
2.3.1 DPC2-11公式模拟实验
根据2.1方法和中国汉族人群基因频率,在单基因座上模拟n组,每组包含3个随机个体(称为1~3号)。在每组中,将1~2号组成混合样本,将3号视为犯罪嫌疑人,1号视为受害人,判断3号、1号和混合样本是否符合混合样本标准。设不符合标准的组的数量为C1,则DPC2-11模拟值(DPC2-11-S)=C1/n。设n=1000万,在Identifiler系统的15个基因座上统计DPC2-11-S。
根据公式(1)和中国汉族人群基因频率,在15个基因座上计算DPC2-11的公式值(DPC2-11-F)。
2.3.2 DPC2-1公式模拟实验
根据2.1方法和中国汉族人群基因频率,在单基因座上,模拟n组,每组包含3个随机个体(称为1~3号)。在每组中,将1~2号组成混合样本,将3号视为犯罪嫌疑人,判断3号和混合样本是否符合混合样本标准。设不符合标准的组的数量为C2,则DPC2-1模拟值(DPC2-1-S)=C2/n。设n=1000万,在15个基因座上统计DPC2-1-S。
根据公式(2)和中国汉族人群基因频率,在15个基因座上计算DPC2-1的公式值(DPC2-1-F)。
2.3.3 DPC2-2公式模拟实验
根据2.1方法和中国汉族人群基因频率,在单基因座上,模拟n组,每组包含4个随机个体(称为1~4号)。在每组中,将1~2号组成混合样本,将3~4号视为2个犯罪嫌疑人,判断3~4号和混合样本是否符合混合样本标准。设不符合标准的组的数量为C3,则DPC2-2模拟值(DPC2-2-S)=C3/n。设n=1000万,在15个基因座上统计DPC2-2-S。
根据公式(3)和中国汉族人群基因频率,在15个基因座上计算DPC2-2的公式值(DPC2-2-F)。
3 结果
Identifiler系统15个基因座的DPC2-11、DPC2-1和DPC2-2的模拟值和公式值如表所示。将单基因座DP值代入多基因座CDP公式[4],计算得Identifiler系统的CDPC2-11=1-1.82910×10-13、CDPC2-1=1-1.98396×10-8、CDPC2-2=1-5.15033×10-22。结果表明:

表 Identifiler系统 DPC2-11、DPC2-1和 DPC2-2的模拟值和公式值
(1)各基因座上,DPC2-11、DPC2-1和DPC2-2的模拟值和公式值均极为接近,因此公式(1)~(3)均符合模拟实验验证。
(2)无论单基因座或多基因座的系统效能对比,均有犯罪嫌疑人和未知个体混合类型<犯罪嫌疑人和受害人混合类型<2个犯罪嫌疑人混合类型。
4 讨论
随着磁珠法自动提取平台的大量应用和扩增试剂盒的进步,DNA检测的灵敏度越来越高,从脱落细胞等检材中检出混合样本分型结果也越来越多,最常见的2组分混合样本分型的解释和分析也越来越重要。虽然2组分混合样本的分类方法和相应LR值计算方法早已有报道[5],但是不管系统效能,仅凭LR值高低单一指标进行统计决策是不可靠的[6]。本实验在2组分混合样本分类基础上,对3种类型的系统效能公式进行数学推导,均符合实验验证。这一结论不仅证明本实验数学公式的有效性,而且进一步体现模拟实验验证方法在法医DNA领域的复杂概率问题中的强大辅助能力。
在全国公安机关DNA数据库基础上,可以根据本实验混合样本判断标准建立混合样本直接比对法。以下分别论述混合样本直接比对法在3种类型中比对价值和实战意义:
(1)犯罪嫌疑人和受害人混合类型是性犯罪案件中最常见的类型,其系统效能(1-1.82910×10-13)高于双亲皆疑鉴定系统效能(1-8.66381×10-11),具有很高的比对价值。传统上根据专家人工拆分该类型混合样本的案例报道[7-9],在Identifiler试剂盒的15个基因座上分别拆分出10、7、12、14个基因座的犯罪嫌疑人分型。专家人工拆分虽然可拆分出较多基因座,但主要依赖于经验和判断,主观性很强,风险很大。Clayton[10]等强调混合样本分析的独立性,即单独分析混合样本的基因型组合,最后才与比对样本进行比较,从而避免人工拆分的先入为主和个人偏好。直接比对法将混合样本和受害人与数据库进行直接比对,可充分利用全部基因座的分型信息,无需录入峰高及峰面积数据,混合比例也无任何影响。因此,在该类型中应用直接比对法方便省力,价值高,风险低,大大优于传统拆分法。
(2)对于犯罪嫌疑人和未知个体混合类型,虽然其系统效能(1-1.98396×10-8)在3个分类中最低,但仍高于三联体鉴定的系统效能(1-1.00239×10-6),同样具有较高的比对价值。无比对样本的2组分混合样本通常最难拆分,需要根据排列组合原理,拆分出多个分型,进行钟摆查询,工作量大,分析复杂[11]。在实际应用中,Pendulum算法中混合样本中主要组分被正确拆分出来且排在第1位的可能性只有50%,主要组分或次要组分均正确拆分且排在前10名的可能性有40%[12]。因此,该类型拆分风险大,可行性低,没有实战意义。与之相比,直接比对法将混合样本与数据库进行直接比对,不产生大量的可能分型,风险较低,具备实战意义。
(3)对于2个犯罪嫌疑人混合类型,其系统效能(1-5.15033×10-22)甚至高于个体识别系统效能(1-7.47208×10-18)。虽然理论上可以进行2个犯罪嫌疑人混合类型的比对,但是实际上不可能如同双亲皆疑的父+母联合录入方法一样联合录入2个犯罪嫌疑人的分型,因此,该类型比对不具备实战意义。实际应用中以犯罪嫌疑人和未知个体混合类型比对来代替。此外,该类型的系统效能高于个体识别,貌似不合常理,但是实际上本实验研究的前提是理想状态下的2组分混合样本。实际检案中,混合样本很难达到理想状态,特别是脱落细胞检材的真峰和伪峰混杂,难以辨认。更大的不确定因素则来自于组分数评估,这也是混合样本鉴定的主要风险之一。周密等人计算表明Identifiler系统中约3.56%的3组分混合样本和0.02%的4组分混合样本可表现为2组分混合样本形式。即使2组分混合样本的组分数评估风险最低,也不能排除高组分混合样本带来的干扰。若考虑组分数评估风险,则该类型的真实系统效能显然低于个体识别。
综上所述,混合样本直接比对法的适用范围广,实战意义大,风险较低,若进一步开发混合样本直接比对软件,则可大大提高公安机关应用混合样本分型比中案件犯罪嫌疑人的能力,为办案指明方向。
[1]郑秀芬.法医DNA分析[M].北京:中国人民公安大学出版社,2002:412-421.
[2]周密,汪军.混合DNA样本的组分数分析[J].刑事技术,2017(1):28-31.
[3]吴薇薇,刘冰,郝宏蕾,等.中国28个省/区汉族人群41个STR基因座多态性数据分析[J].中国法医学杂志,2016(1):27-32.
[4]周密,韦帆.两个个体混合样本似然比率分析法的研究[C]//葛百川.DNA数据库建设应用成果与展望IV.北京:中国人民公安大学出版社,2015:409-414.
[5]郑秀芬,纪贵金.二组分混合样品DNA结果解释[J].中国法医学杂志,2000(4):203-207.
[6]侯一平.法医物证司法鉴定实务[M].北京:法律出版社,2013:222-224.
[7]陈蓉华,侯杰,晏斌,等.成功拆分混合样本破获强奸案1例[J].法医学杂志,2014(1):78-79.
[8]李旭鹏,张玉红,贾东涛,等.混合基因型拆分分析1例[J].中国法医学杂志,2011(3):246-246.
[9]苑美青,李万水,康艳荣,等.混合样本拆分查询犯罪嫌疑人的应用研究[J].刑事技术,2012(6):5-7,12.
[10] Clayton T M, Whitaker J P, Sparkes R, et al. Analysis and interpretation of mixed forensic stains using DNA STR profiling[J]. Forensic Science International,1998(1):55-70.
[11] 陈静,徐秀兰,李万水,等.混合样本拆分结合快速协查比对平台破获命案积案[C]//葛百川.DNA数据库建设应用成果与展望IV.北京:中国人民公安大学出版社,2015:228-230.
[12] Bill M, Gill P, Curran J, et al. PENDULUM—a guideline-based approach to the interpretation of STR mixtures[J]. Forensic Science International,2005(2-3):181-189.
Experimental Research of System Effectiveness in Mixed Sample with 2 Components
ZHOU Mi1,2Wang Jun2
(1 Criminal Police Detachment of Wuhu Public Security Bureau Anhui Wuhu 241000;2 School of Computer & Information Science of Anhui Polytechnic University Anhui Wuhu 241000)
The system effectiveness of the mixed sample with 2 components is derived by formula, which is verifi ed by random simulation. Firstly, 3 kinds of exact defi nition of system effectiveness in mixed sample with 2 components were established, and the corresponding mathematical formulas were derived based on the defi nition. 3 kinds of formula values were calculated in 15 STR loci of Identifi ler system. Secondly, 3 kinds of simulation values were counted through multi-group simulation experiments in 15 STR loci. Finally, 3 kinds of formulas were empirically validated by correlation method between the formula values and simulation values. The result shows that 3 kinds of formulas are all in accord with the simulation experiments. In Identifiler system, system effectiveness of suspect and victim type (CDPC2-11) was 1-1.82910×10-13, system effectiveness of suspect and unknown type (CDPC2-1) was 1-1.98396×10-8, system effectiveness of 2 suspects type (CDPC2-2)was 1-5.15033×10-22. 3 kinds of formulas could be applied to the calculation of system effectiveness in mixed sample with 2 components.
Mixed sample System effectiveness Stochastic simulation method
DF795.2
A
2095-7939(2017)05-0090-06
10.14060/j.issn.2095-7939.2017.05.018
2017-05-12
安徽省科技强警资助项目(编号:1604d0802002)。
周密(1982-),男,安徽芜湖人,安徽省芜湖市公安局刑警支队主检法医师,主要从事法医物证学研究。
(责任编辑:孟凡骞)
