绞吸式挖泥船电力驱动系统建模与仿真研究*
2017-11-02范世东司宇航刘恩东
胡 佳 高 岚 范世东 司宇航 刘恩东
(武汉理工大学船舶动力工程技术交通行业重点实验室 武汉 430063)
绞吸式挖泥船电力驱动系统建模与仿真研究*
胡 佳 高 岚 范世东 司宇航 刘恩东
(武汉理工大学船舶动力工程技术交通行业重点实验室 武汉 430063)
为了研究直接转矩控制(DTC)调速策略在电力驱动绞吸式挖泥船上的适用性,基于饱和沙二维切削理论建立绞刀切削模型,基于泥泵特性及管道流体力学理论建立泥浆输送系统模型,在此基础上基于异步电动机数学模型和直接转矩控制理论建立绞刀和泥泵电力驱动系统模型.根据施工实际建立仿真模型并基于典型工况对直接转矩控制系统进行仿真实验,分析绞吸式挖泥船在典型工况下驱动系统的调速性能和船舶电站的稳定性.仿真结果表明,直接转矩控制系统具有良好的调速性能,同时能保持电力系统的稳定性,在绞吸式挖泥船疏浚设备驱动系统中有良好的适用性.
绞吸式挖泥船;电力驱动;绞刀和泥泵;直接转矩控制
0 引 言
绞吸式挖泥船作为一种主要的疏浚设备在港口航道的改良以及各种吹填作业中发挥了巨大的作用.其主要施工设备为绞刀和泥泵,在施工作业过程中需要对绞刀和泥泵进行驱动控制,传统的驱动方式包括液压驱动、柴油机直驱和柴油发电机组电驱,而如今电力驱动已逐渐成为设计的主流方向[1].相较于传统的驱动方式,采用全电力驱动既节省了挖泥船布置空间,又提高了能源利用效率,但是同时也带来了绞刀和泥泵电机的控制问题.由于绞吸式挖泥船经常需要在不同水域施工作业,因而其施工工况不是一定的,为了保障挖泥船在各种工况下都能有良好的疏浚效率,需要绞刀和泥泵驱动系统具有较好的调速特性和转矩跟随性能[2].因而研究分析绞吸式挖泥船电力驱动系统驱动性能对保障其正常作业并提高疏浚效率有很大的意义.
为了研究基于直接转矩控制(DTC)的异步电动机绞刀和泥泵驱动系统在绞吸式挖泥船上的驱动性能,本文基于饱和沙切削理论及流体力学相关理论分别搭建了绞刀与泥泵及泥浆输送管道数学模型,基于异步电动机特性和直接转矩控制理论建立了电力驱动系统模型.在Matlab/Simulink仿真平台上搭建全电力驱动绞吸式挖泥船电力系统仿真模型,基于典型工况进行仿真实验,分析该系统的驱动性能和控制效果.
1 绞刀模型
当绞刀切削速度在0.5~5 m/s之间时,此时膨胀现象为影响切削过程的主要因素[3],可以建立此切削过程的平衡方程:
(1)
(2)

(3)
式中:km为平均渗透率,km≈0.5ki+0.5kmax,ki为初始渗透率,kmax为最大渗透率;Fh为切削力水平分量;Fv为切削力垂直分量;ρw为水密度;g为重力加速度;vc为切削速度;hi为初始切割层厚度;b为刀片宽度;e为体积应变系数.
系数c1,c2为切削系数,其表达式为
c1=
(4)
c2=
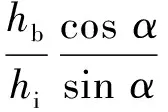
(5)
式中:φ为土壤的内摩擦角;δ为泥土表面摩擦角;α为刀片切削角;hb为刀片高度;h为土层厚度.
当切削速度大于5 m/s时,此时切削力取决于开挖水域水深,气隙压力和切削力始终保持相等,因此可以得到两个切削方程:
Fh=d1ρwg(z+10)hib
(6)
Fv=d2ρwg(z+10)hib
(7)
式中:d1,d2为此时切削系数
为了应用二维切削理论对绞刀进行建模分析,需要进行一些假设[4]:①在整个计算过程中参数c1,c2,d1和d2为定值,即平均切削层厚度不变;②绞刀是顶角为ξ的冠状型绞刀,刀片和绞刀轴之间夹角为ι.
切削层厚度可表示为
hi=himaxsinΩsinξ
(8)
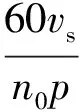
(9)
式中:hi为初始切割层厚度;himax为最大切割层厚度;Ω为绞刀切削元件覆盖角;vs为横移速度;n0为绞刀转速;p为绞刀刀片数.
绞刀头的假定刀片宽度为
bpr=bcosιcosξ
(10)
式中:bpr为绞刀投影在轴上的刀片宽度.
绞刀切削速度为
vc=vciRcosι+vs
(11)

(12)
式中:vciR为绞刀圆周速度.
绞刀在各个方向的受力情况为
Fa=Fhsinιcosξ-Fvsinξ
(13)
横移摆动方向的受力为
Fs=FhcosιcosΩ±
(-Fhsinιsinξ+Fvcosξ)sinΩ
(14)
与摆动方向和轴向垂直方向的受力为
Fv=±FhcosιcosΩ-
(-Fhsinιsinξ+Fvcosξ)sinΩ
(15)
对于半径为R,刀片投影宽度为bpr的绞刀,其瞬时转矩为
M=FhcosιR
(16)
平均切削力可以对切削范围角Ω0内绞刀瞬时切削力进行积分再与刀片数相乘获得[5],即
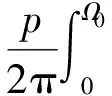
(17)
由以上可以得出,当切削速度在0.5~5 m/s范围内时,可得绞刀转矩为
(18)
由于绞刀横移速度vs较小,在计算切削速度vc时可将其忽略不计,此时
vc≈vciRcosι
(19)
(20)
2 泥浆管道疏浚系统模型
绞吸式挖泥船所使用的泥泵一般为离心泵,它靠叶轮带动液体高速旋转而将机械能传给液体.具有结构紧凑、扬程范围广、运转平稳、振动小等优点.
离心泵相似关系为
在进行输排泥作业过程中,泥浆输送管道的水头损失包括四个部分[6]:
1) 吸排泥前后由排高会造成一部分的水头损失:
H1=Zdβ m
(21)
式中:dβ m为泥浆相对密度;Z为排高.
2) 当泥浆输送管道在输送清水时,由水流与管壁相互作用形成的沿程阻力损失为
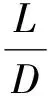
(22)
式中:λ为磨阻系数;L为管道长度;D为泥泵直径;v为泥浆流速;g为重力加速度.
对于均匀流体来说,输送泥浆时的沿程阻力损失H21可以在输送清水的基础上进行计算.
H21=H×dm
(23)
式中:H为泥泵的总扬程.
当管道中泥浆为非均匀流体时,单位长度管道的水头阻力损失为
(24)
式中:vs为颗粒沉降速度;m为根据土质及泥浆浓度所得系数;ds为颗粒直径;Kd为试验系数.
3) 由管道铺设情况引起的局部阻力水头损失H3为
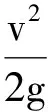
(25)
式中:ξj为局部阻力系数.
4) 由于管路出口流速大于入口流速,即泥浆在疏浚管道中动能增加,此部分水头损失H4为

(26)
式中:v2为管道排泥管泥浆流速.
综上,绞吸式挖泥船输排泥管道满足如下方程
∑Δpi=ρmgHt+Δpm+
(27)
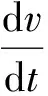
由伯努利方程可得
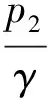
(28)
式中:γ为重度;p1,p2为泥泵进、出口压力,v1,v2为泥泵进、出口流速;Z1,Z2为泥泵进出口位置距水平面的高度.
通常绞吸式挖泥船泥浆输送管道出口管径大于入口管径,因此泥浆进出口流速不同,但同一管道中流量相同[7],即
v1A1=v2A2
(29)
式中:A1,A2为不同管段的横截面积;v1,v2为泥浆流速.
由离心泵性能曲线可知,扬程和管道流量的平方成正比,即
H=kQ2
(30)
挖泥船瞬时产量为

(31)
式中:W为产量值;D1为输泥管内径;ρw为水的密度;ρ0为原状土的密度.
3 异步电机直接转矩控制
对基于三相静止坐标系的异步电动机模型进行Clark变换后可得其电压公式[8]
(32)
式中:α,β对应三相坐标系中空间矢量的α分量和β分量.
由式(32)可得定子磁链公式
(33)
电极电磁转矩公式
Te=np(isβψsα-isαψsβ)
(34)
或:
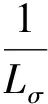
(35)
式中:Te为电磁转矩;np为电机极对数;θ为磁通角(rad).
运动公式:
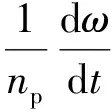
(36)
式中:TL为负载转矩;J为转动惯量(kg·m2).
电磁转矩的生成可看成是定子磁场和转子磁场相互作用的结果,电磁转矩可表达为
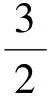
(37)
式中:ψs为定子磁链;θ为定子磁链和转子磁链之间的夹角.转子磁链ψr与负载有关,而为保证电机驱动性能,定子磁链幅值通常保持不变,则可以通过控制磁通角θ控制电磁转矩的大小[9].
电机定子电压方程为
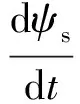
(38)
忽略定子电阻的影响,则有
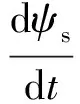
(39)
所以可以通过外加电压us来控制定子磁链的幅值和转速.在很短时间内依靠us的作用使定子磁链加速旋转,而这期间转子速度来不及变化,由此可加大磁通角θ,若保持定子磁链的幅值不变,就可以使电磁转矩增大;若使定子磁链反向旋转,可使电磁转矩减小.
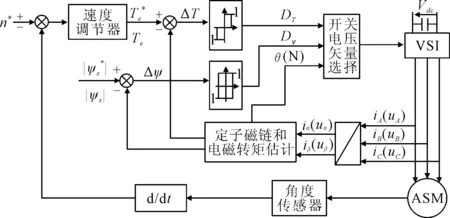
图1 异步电动机直接转矩控制原理图
本文拟用异步电动机直接转矩控制系统(DTC),见图1.系统组成为速度调节器、滞环比较器、电压矢量开关表、Clark变换、磁链和转矩观测器,角度传感器、电压源逆变器和异步电动机(ASM).系统将检测的定子三相电流iABC经过Clark变换后输入磁链和转矩观测器,估算出定子磁链和转矩的大小分别与磁链和转矩给定值做比较,其差值分别经过滞环比较器得到磁链控制信号Dψ和转矩控制信号DT,然后根据定子磁链位置、转矩控制信号DT和磁链控制信号Dψ,利用电压矢量开关表选择响应的电压矢量控制逆变器开关的通断,驱动电机运行.其中磁链给定信号为常数,转矩给定信号由实际转速与给定转速的差值经速度调节器得到的.该过程将转矩和磁链作为反馈信号,省去复杂的矢量变换,直接控制电磁转矩,从而达到调速的目的.
4 仿真分析
基于以上分析所得数学模型,在仿真平台建立全电力驱动绞吸式挖泥船电力系统仿真模型见图2.
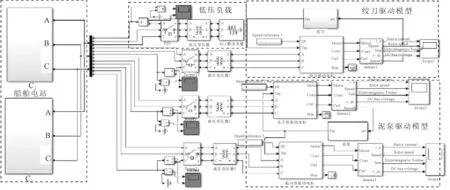
图2 全电力驱动绞吸式挖泥船电力系统仿真模型
本文以某3 500 m3/h绞吸式挖泥船为母型船,具体参数设置如下:船舶电站由两台功率为3 388 kVA的柴油发电机组组成,额定电压6.6 kV,额定频率50 Hz,功率因数0.8.绞刀和泥泵电机额定功率为1 500 kVA,额定电压3.3 kV,额定频率50 Hz,静态负载功率为600 kW.疏浚作业系统参数:绞刀为冠状型,绞刀半径R=1.34 m,刀片宽度b=0.07 m,刀片与绞刀轴夹角ι=80°,切削系数c1=0.3,体积应变系数e=1,平均渗透率km=10.5×10-5m/s,吸排泥管径D=900 mm,泥浆体积分数为20%.
4.1 理想工况
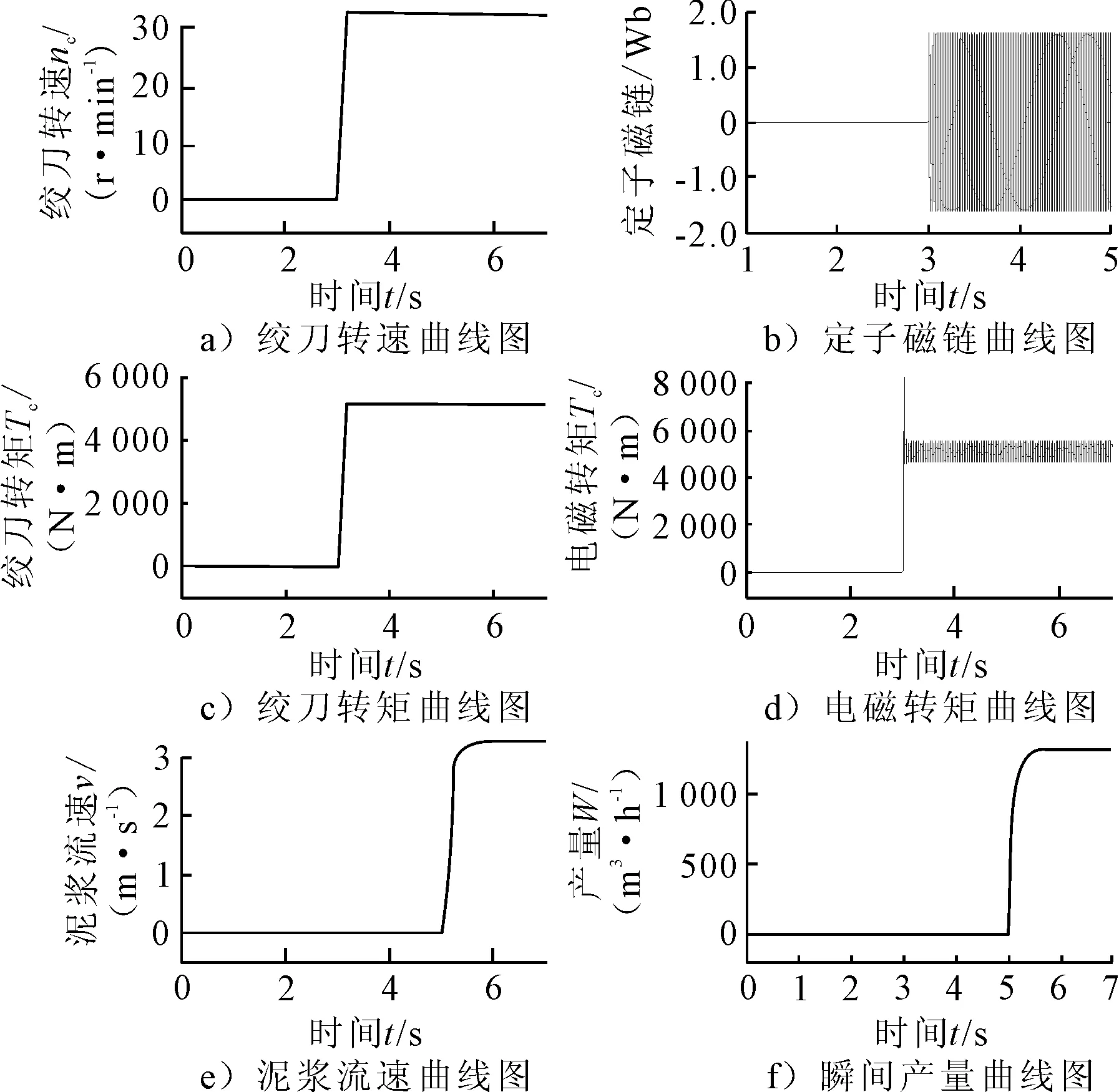
图3 理想工况下挖泥船主要参数曲线图
当疏浚条件较好且不需要大排距时,此时认为疏浚过程中绞刀的机械转矩保持不变,吸排泥管中泥浆为均匀流移.仿真时间设为7 s,在1 s时投入静态负载,在3 s时投入绞刀电机,在5 s时投入单台水下泥泵电机.仿真结果见图3.由图3a)可知,在理想的施工条件下,t=3 s时绞刀电机启动,绞刀转速上升,在t=3.1 s时达到稳定值,此时绞刀转速稳定在31 r/m.同时随着绞刀转速的增加,其机械转矩在转速稳定同时达到稳定值Tc=5 200 Nm.由图3d)可知,电机电磁转矩随着绞刀机械转矩的建立在短暂波动后保持在5 200 N·m附近波动.运行过程中电机定子磁链幅值稳定在设定值1.5 Wb左右.
由图3e)可知,在t=3 s时水下泥泵电机启动,在经0.6s后,在t=5.6 s时管道中泥浆流速达到稳定值vm=3.6 m/s,同时挖泥船的瞬时产量达到W=1 310 m3/h,由于挖泥船实际产量受到不同施工区域土质影响很大,以本文施工对象砂土为例,其孔隙率一般为0.3~0.8,即使是在输送同样密度的泥浆时,由于土层孔隙率的差异其产量也大不相同.因而本文仿真实验中关于挖泥船瞬时产量值只能用来反映其驱动电机的驱动效果,不能精确表示此种工况下的产量值.
以上仿真实验结果表明,在理想工况下,绞刀和泥泵电机的驱动效果良好,由于直接转矩控制具有快速响应性能,电机启动性能良好,在绞刀和泥泵机械转矩建立时,电机电磁转矩能快速响应.
4.2 实际工况
在实际施工过程中,疏浚条件往往比较恶劣并且需要大排距.此时疏浚作业过程中,由于开挖条件恶劣,使得绞刀机械转矩波动,同时由于此时管道内泥浆为非均匀流移,因此在吸排泥过程中泥泵也受到扰动.1 s时投入静态负载,3 s时投入绞刀电机,5 s同时投入水下泵和舱内泵电机,在绞刀和泥泵运行时对其施加随机附加转矩,仿真实验结果见图4.

图4 实际工况下挖泥船主要参数曲线图
由图4a)可知,在t=3 s时绞刀电机启动,同时在绞刀开始转动时,其机械转矩受到来自开挖土层的扰动,由于绞刀的机械转矩受到扰动,而机械转矩由切削力和切削力臂决定,较刀的切削力臂长度由绞刀的外径和其形状决定,在施工过程中可以看作定值,因此当绞刀机械力矩受到扰动时,土壤对其切削反作用力也受到扰动,从而引起绞刀转速的变化.因此可以得出绞刀的转速变化与其机械转矩的变化相反,图4a)和图4c)反映出了这一变化关系.由图4c)~d)可知,当绞刀机械转矩受到随机扰动在5 000 N·M附近波动时,电机电磁转矩也随着绞刀机械转矩波动的方向在5 000 N·M附近波动,说明绞刀电力驱动系统跟随性能良好.当t=5 s时泥泵电机起动,短时间内泥泵转速上升到额定转速附近,由于受到管道内非均匀流移对泥泵叶片产生的作用力持续改变的影响,管道内泥浆流速在6.5 m/s附近小幅波动,对应的疏浚系统瞬时产量在3 300 m3/h附近波动,如前所述,此产量值只能反映其驱动特性.图5为实际工况下绞吸式挖泥船电站主要参数曲线.
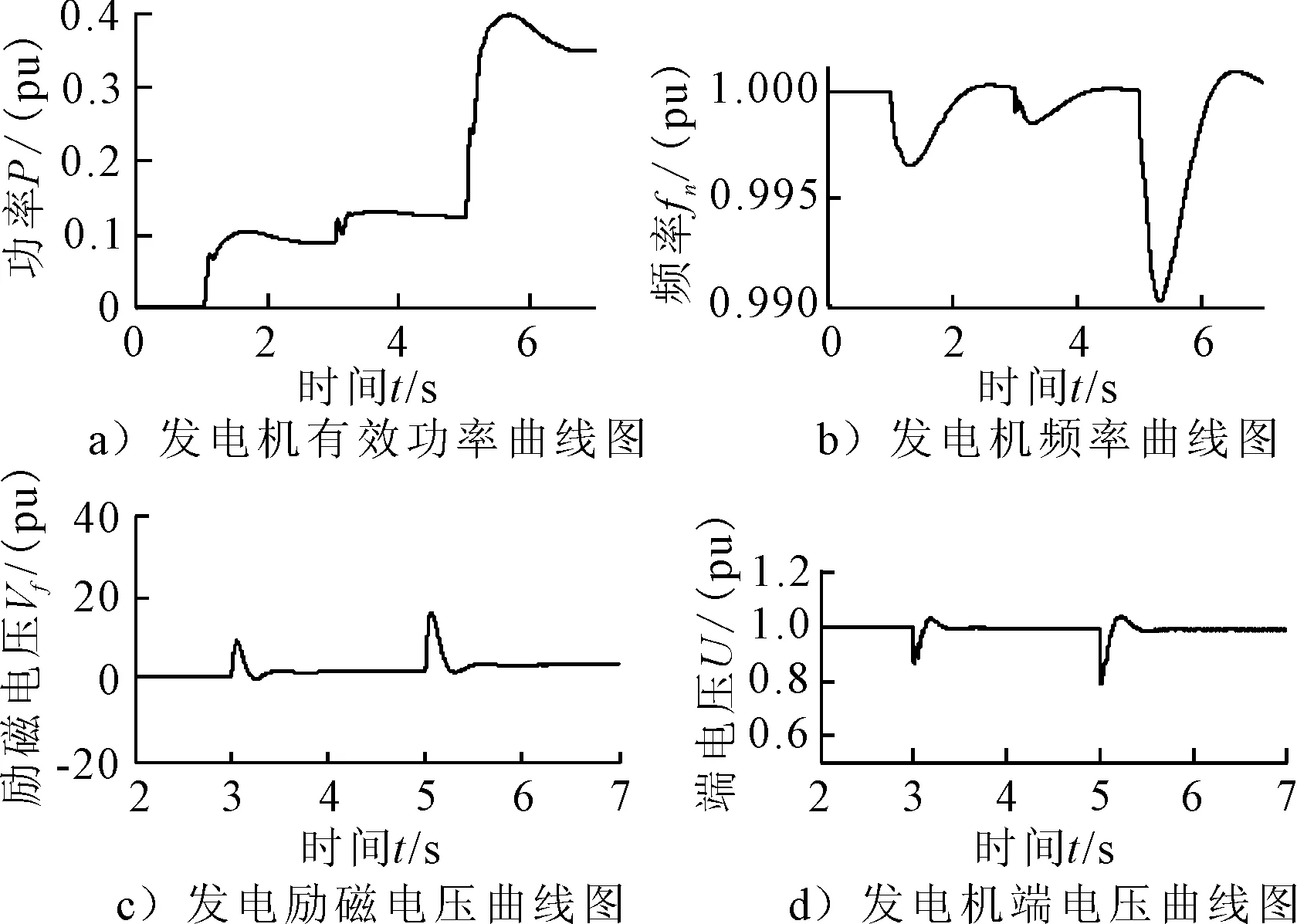
图5 船舶电站主要参数曲线图
由图5a)可知,随着负载的依次投入,发电机组输出功率依次增加.由图5a~c)可知,在绞刀和泥泵投入时,电网频率和发电机端电压均发生短暂的突降,并快速回复稳定.在发电机端电压降低的同时,励磁控制系统提高发电机励磁电压以补偿端电压的压降.当系统进入稳态时,由于负载的投入使得电网电流增大,从而使得电阻压降增大,发电机端电压出现稳态偏差.以上电网主要参数的变化情况均符合文献[10],可以得出异步电动机DTC系统在全电力驱动绞吸式挖泥船中作为绞刀和泥泵的驱动系统有一定的适用性.
5 结 论
1) 直接转矩控制系统具有良好的快速响应性能,能较好的适应绞吸式挖泥船施工作业过程中工况的变化.
2) 采用直接转矩控制策略能在保证船舶电网稳定性的前提下有效的提高疏浚效率,在全电力驱动绞吸式挖泥船上有较好的适用性.
[1] 邹学义.3 000 m3/h绞吸式挖泥船电气设计[J].江苏船舶,2010,27(4):26-29.
[2] 陈梦.大型绞吸挖泥船电力驱动系统研究[D].上海:上海交通大学,2013.
[3] MIEDEMA S A. The cutting forces in saturated sand of a seagoing cutter suction dredger[J]. Terra Et Aqua,1989(1):55-58.
[4] 王翰涛.绞吸式挖泥船电控绞刀工作特性研究[D].济南:山东理工大学,2015.
[5] VAN A G,LEUSSEN W V. Basic research on cutting forces in saturated sand[J]. Geotechnical Engineering,1987,113(12):1501-1516.
[6] 师光飞.耙吸式挖泥船泥浆与管道输送的建模与仿真[J].船海工程,2010,39(5):46-49.
[7] 张兴荣.管道水利输送[M].北京:中国水力水电出版社,1997.
[8] 张细政.复杂电机系统的混合滑模变结构控制方法及其应用研究[D].长沙:湖南大学,2010.
[9] 张俊喜.异步电动机直接转矩控制系统研究[D].哈尔滨:哈尔滨理工大学,2007.
[10] 中国船级社.钢制内河船舶建造规范[S].北京:中国船级社,2015.
The Modeling and Simulation Research on the Electric Drive System of Cutter Suction Dredger
HUJiaGAOLanFANShidongSIYuhangLIUEndong
(KeyLaboratoryofMarinePowerEngineeringandTechnology,MinistryofTransportation,WuhanUniversityofTechnology,Wuhan430063,China)
To study the applicability of direct torque control (DTC) strategy in electric drive cutter suction dredger, a cutting model of the cutter based on saturated sand two-dimensional cutting theory and a mud transporting model based on mud pump characteristic and pipeline fluid mechanics theory are established, respectively. Based on the mathematical model of asynchronous motor and direct torque control theory, the cutter and mud pump electric drive system model is established. According to the construction practice, the simulation model is built and simulation experiment is carried out on the DTC system based on typical conditions. The speed performance of electric-drive system and stability of the power station has also been analyzed. The results show that the DTC system has a good speed performance and can maintain the stability of the power system. It’s applicable on the driving system of the dredging equipment of the cutter suction dredger.
cutter suction dredger; electric drive; cutter and mud pump; direct torque control
U664
10.3963/j.issn.2095-3844.2017.05.032
2017-08-15
胡佳(1991—):男,硕士生,主要研究领域为轮机仿真及自动化
*国家自然科学基金项目资助(51179144)
