探究性教学在高中数列教学中的应用
2017-11-02龙易程
◆龙易程
探究性教学在高中数列教学中的应用
◆龙易程
本文结合高中数学数列的相关内容,提出了在数列学习过程中应当带着问题,探究数列的概念、定义、公式。并通过分析一些典型例题加以解析,以此提高解题能力,巩固所学。
数列;探究;概念;公式;解决问题
一、关于数列
结合教材来看,数列部分的内容无非就是其定义、共享公式、数列求和、等比、等差数列在现实生活中的应用。在学习过程中可以用如下概念图来构成数列的知识体系。
概念是数学逻辑的起点,认知的前提,还是数学思维的核心,是数学思维的细胞,是数学方法、解决问题的基本前提,是客观现实当中空间形式和数量关系的本质属性在人脑中的反映。在学习数列过程中首先要对数列的概念和定义有一个清晰的认识,然后结合问题产生认知冲突,进而在探究中不断完善数列的知识体系。所以在数列学习中运用探究学习法,首先就需要对概念进行探究。然后探究数列的公式,最后探究具体的数列问题。
二、关于数列的探究性学习
探究数列概念。在探究数列概念时需要明确这部分内容的重难点,即数列定义的归纳与认识以及数列与函数的联系和区别。在学习过程中把握重难点,从日常生活提炼一些经验来指导数列概念的探究。比如,在一些施工工地上,经常可以看到一些堆放在一起的圆钢,可能在最下层有100根,上面一层有99根,以此类推。如果这样放置,最多可以堆放多少层,或是某一层有多少根,又或者从第一层到第n层共有多少根。带着这些问题进入数列的学习。
归纳数列的定义,可以回顾学过的关于映射和函数的知识,回忆函数的定义,然后给出一列数,如1,2,3……50;15,5,16,16,18;0,10,20,30……101等等。通过分析这些数来分析其中的规律,进而得出数列的定义——按一定次序排成的一列数。此时就可以发现上述问题中隐含的规律,就可以用数列来表示,但是如何计算还是成问题。所以就需要对数列的公式进行探究。
探究数列公式。结合上述例子,第一层有100根圆钢,那么在数列中就是第一项,然后第二层有99根为第二项,依次类推到第n项。如果从1数到50,在数列中,每一个项的序号与数是对应的,此时,每一项就与其相对应的序号一致,用公式来表示就是an=n(1≤n≤50)。如果以0,10,20,30……101这组数来看,探究其中数与对应序号的关系,可以得到第一项用10*(1-1)来表示,第二项则是10*(2-1)。依次类推,就可以得出an=10(n−1)(1≤n≤101)。要注意an是数列的第n项,n表示项的序号,这就是数列的通项公式,从函数的知识点来看,通项公式相当于函数解析式,这样就可以利用画图的方法来表示数列比如1,3,5,7……这一列数。它的通项公式为,画出图像为图2。
此时上文例子中的一些问题迎刃而解,比如求第57层有多少圆钢,显然若能够推导出它的通项公式[an=100−n(1≤n≤9)]就可以比较简单地计算出来(答案43根),考虑实际生活经验,最顶层最多只能放置1根圆钢。反向探究,如果第一层有100根圆钢,最多只能叠加99层。但是从第一层到某一层的所有圆钢数量依然无法解决,那么可以通过探究前n项和公式,然后再来解决问题。

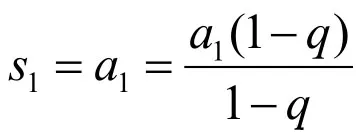
探究数列问题。探究数列问题也就是在掌握上述概念、定义、公式的基础上,解决实际的应用问题。在这个过程中可以进行解法探究、变式探究从而培养发散思维能力。以解法探究为例,主要就是一题多解。
例题:等差数列{an},前10项和为100,前100项和为10,求前110项的和。
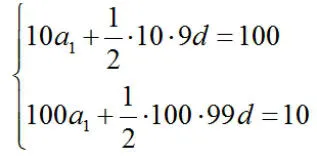

结束语
综上所述,在学习数列的过程中,关键是要发挥主观能动性,积极主动地探究数列的知识,形成知识体系。带着问题去学习,不断解决问题,不仅能够提高解题的能力,还能养成数学思维能力,使学习事半功倍。
[1]飞超.浅论探究式教学在高中数学课堂教学中的应用[J].中国校外教育,2016,26:31-32.
[2]王海伟.探究式合作法在高中数学教学中的应用分析[J].西部素质教育,2015,05:106.
(作者单位:湖南省长沙市第一中学)
