我国社会消费品零售总额预测方法与实证分析

◆王 哲 颜卫忠

我国社会消费品零售总额预测方法与实证分析

◆王 哲 颜卫忠

本文通过对我国社会消费品零售总额的影响因素进行分析,建立线性回归方程对2015年社会消费品零售总额进行预测。再通过时间序列分析方法中的时间序列模型 (ARIMA)，对我国2015各月份社会消费品零售总额进行预测。通过对比两种预测方法，时间序列模型预测结果较为准确，可为政府决策提供科学依据。

社会消费品零售总额；多元线性回归；时间序列；ARIMA模型

引言

通过近40年的数据显示，我国消费品的零售总额有了较好的发展趋势，而消费品零售总额包含了许多影响因素，比如教育业、零售批发贸易业、旅游业、餐饮业、建筑业等其他行业。如今研究消费品零售总额]的现状对我国经济增长起着非常重要的作用，因此探讨我国消费品零售总和的影响因素和分析其影响因素的影响程度帮助我国政府出谋划策极为重要。

根据计量经济学相关知识理论及前人所写文章研究经验可得,社会消费品零售总额y（亿元）的主要影响因素有: 城镇居民家庭人均可支配收入水平指数x1（1978=100）、农村居民家庭人均纯收入水平指数x2（1978=100）和商品零售价格指数x3。

一、模型的建立与求解

本文把因变量记为 ，三个自变量分别记为：x1,x2,x3。

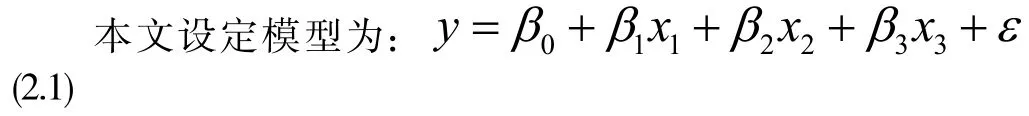
其中β0,β1,β2,β3是模型参数，ε为绝对误差项。本文知道在多元线性回归模型中，对误差项ε有三个基本假定：

1.正态性。即：E(ε)=0

2.方差齐性。即：var(ε) =σ2

3.独立性。对于自变量x1,x2,x3一组特定值，ε所对应的与ε任意一组其他值不相关。同样，对于给定x1,x2,x3的值，因变量y也是一个服从正态分布的随机变量。

（一）模型的求解（多元回归参数估计）

本文所建立的多元线性回归方程含有未知参数β0,β1,β2,β3。而要求出各个参数值，本文采用采用最小二乘估计法，其基本思想也就是寻找参数β0,β1,β2,β3的估计值，而使离差平方和达到极小，即寻找β0,β1,β2,β3满足：

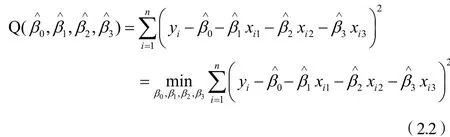
本文通过1995-2012年的数据建立多元线性回归模型，通过利用OLS进行参数估计。由SPSS的运行结果可得回归方程为：

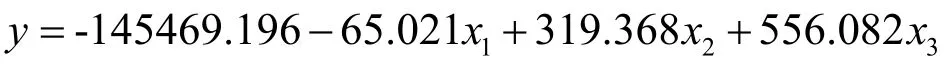
由R2=0.998知，拟合结果良好。从此方程本文可以看出这三个影响因素对本文因变量影响还是比较显著的，得出y与x1呈负相关关系，而y与x2和x3呈正相关关系。

由SPSS知F=2366.824＞F0.05(3,14)=3.34即回归方程通过了F检验（α=0.05）。由上表可知p＜0.05，表明回归方程在α=0.05是显著的，所以该模型上可以看出社会消费品零售总额与所有自变量在整体之间呈线性关系显著，此模型则通过该检验。

（二）预测

求出了y（亿元）与x1（1978=100）、x2（1978=100）和x3的回归方程。现用1995-2012年的各个自变量取值进行趋势预测，得到2013-2015年x1（1978=100）分别为1241.59、1342.78、1449.05，2013-2015年x2(1978=100)分别为1313.27、1465.97、1637.62。由国家统计局得到2013-2015年x3分别为101.4、101、100.1。将这些数据带入到所求出的方程，可以得到2013-2015年的社会消费品零售总额y的预测值分别为249604.5088亿元、291570.0946亿元、338979.3563亿元。

二、基于时间序列ARIMA的预测模型

（一）研究方法介绍

ARIMA模型[1]的基本思想是由于本文所要研究的一组数据中一部分时间序列是依赖于时间t的变化而变化，虽然该研究数据会存在单个序列值会具有不确定性，但总体来说本文所研究数据时间序列的变化具有一定的规律性。经过对该数学模型的分析研究，可以更进一步地认识时间序列的结构与特征，使得方差最小。其步骤为：1.首先将所收集的原始数据的序列进行平稳化。确定d和D的取值。2.第二步则需识别模型的阶数。3.最后需要进行模型诊断。

（二）模型运用

本文利用2009年1月—2014年12月全国社会消费品零售总额数据进行预测：

由SPSS中做出来的ACF图可以看出，一阶季节差分后的序列是平稳的。ACF图和PACF图中各有一个非常明显的峰值，因此取p=1,q=1，经过一阶差分和季节差分后的ACF和PACF图，可以看出ACF和PACF图中各有两个极为明显的峰值，因此得出P=2,Q=2。因为之前经过数据处理都可以确定为一阶差分，所以.最后所选取的模型则为。

则通过时间序列模型所预测出2015年社会消费品零售总额为291653亿元。

图1给出了各月的销售额及其预测结果。从拟合程度看效果非常好。

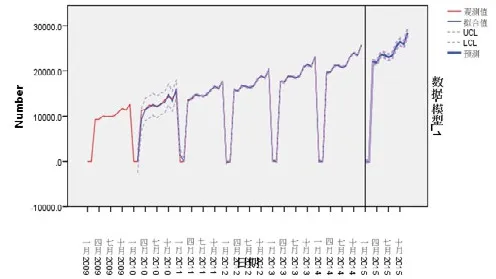
图1 ARIMA(1,1,1)(2,1,2)12模型预测

模型诊断：由SPSS得出的ACF和PACF图可以判断出残差已经是白噪声序列，表明我们所选择的ARIMA(1,1,1)(2,1,2)12模型是正确的。且R2=0.99，更进一步说明了模型的正确性。我们查阅到2015年社会消费品零售总额真实值为300930.8亿元，可知ARIMA模型预测的值更接近真实值。

三、模型评价

通过线性回归模型得到的这个线性方程也具有一定的经济意义，可以为我国较为粗略地解释一些经济现象。而ARIMA模型更倾向于短期预测，没有考虑预测期相应时间内突发情况等因素。所以在短期内时间序列模型的预测结果可为政府提供相应的政策。

四、 政策建议

（一）由研究结果可知，影响社会消费品零售总额的主要因素在于农村居民家庭人均纯收入水平指数，所以我国政府应该积极鼓励农民，对有农田的人进行农田自然灾害补助、生活补助，及时了解消费状态。

（二）缩小城镇农村差距，推动城镇农村一体化。城乡空间布局一体化，现在人们都挤破头朝城市发展，可以考虑将工业引进城乡发展一体化中。

（三）刺激旅游消费。随着人民生活对生活质量的要求提高，旅游业也逐渐发展起来。因此我们可以借此机会把农村经济带动起来。可以在农村进行投资，比如度假村，农家乐等借用农村较好的生态环境吸引城镇居民，从而刺激消费提高农村经济。

[1]贾俊平.统计学第四版[M].北京:中国人民大学出版社,2011.189-196.234-249.

[2]陈斌,张卫华.我国社会消费品零售总额的影响因素分析[J].广西师范学院学报(哲学社会科学版),2010,31:30.

[3]毛敏芳,魏晓平.基于社会消费品零售总额的个人消费行为分析[J].沿海企业与科技,2006,3:10-11.

[4]黄彦.基于ARIMA 模型的我国社会消费品零售总额实证分析[J].经济论坛.2011,11:31-36.

[5]薛薇.spss统计分析方法及应用第三版[M].北京:电子工业出版社.2014,367-370.

（作者单位：西安财经学院）